ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПРИ ИЗГИБЕ

 

СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ

СОКРАЩЕННЫЙ КУРС) Составитель И.К.Калько

/ С

 

Барнаул 2006

Глава IX

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПРИ ИЗГИБЕ

ОБЩИЕ ЗАМЕЧАНИЯ

Вычисленные напряжения позволяют проверить прочность систе­мы. Однако весьма" прочные балки могут оказаться непригодными к эксплуатации из-за…   В настоящей главе рассмотрим только такие балки, у которых поперечное сечение имеет ось симметрии, а все силы,…

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ОСИ ИЗОГНУТОГО БРУСА

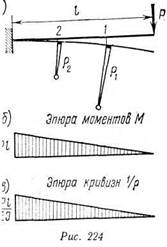
1 VI Формула (9.3) показывает, что кривизна изменяется по длине , ' М _

Г,- = const.

Р LJ

Отсюда следует, что радиус кривизны — также величина постоянная. Таким образом, при чистом изгибе балка изгибается но окружности. Однако в общем случае непосредственно применять закон измене­ния кривизны для определения прогибов не удается. Для аналитиче­ского решения задачи используют известное из математического анализа выражение кривизны

Подставляя значение кривизны в равенство (9.3), получим диф-гренциальное уравнение оси изогнутого бруса

d²v
± **______ _s« (9 4)

Интегрирование этого нелинейного дифференциального уравнения

связано с большими трудностями. Учитывая, что на практике при­ходится иметь дело с малыми проги­бами и что тангенсы углов наклона

dv „ ,

-г касательной к оси будут ма­лы, квадратом первой производной

ldv-в знаменателе {-, по сравнению

^с единицей можно пренебречь*.

згда получим приближенное дифференциальное уравнение

Два знака в уравнении (9.5) поставлены потому, что знак кривизны «к -г? может не совпадать со знаком изгибающего момента. Знак швизны зависит от направления осей координат. Знак изгибающего

* Для рассмотренного в § 74 примера изгиба консольной балки по окружности шсимость между прогибом и углом поворота сечения конца консоли устанав-вается выражением (а), откуда следует

W.v 2v

(же при сравнительно невысоких требованиях, предъявляемых к жесткости балок ждуэтажных перекрытий, должно быть

V . 1

/ " 200■

'АЛ

мдрат тангенса угла попорота сечения а = I - j _ч имеет порядок

^доватслыю, данной величиной по сравнению с единицей можно пренебречь.

момента был выбран в зависимостн от того, где расположены растяну тые волокна. Так, например, для случая, когда ось Оу направлен, вверх, положительному моменту (рис. 226, а) соответствует положи тельная кривизна, а отрицательному — отрицательная кривизна.

Таким образом, в случае, когда ось Оу направлена вверх, знаки кривизны и изгибающего момента совпадают, поэтому в дифференциаль­ном уравнении берется знак плюс:

^diP _ .1, ^м dz* ^r EJ'

■ Если ось Оу направлена вниз, то знаки у кривизны и изгибающего

момента различны (рис. 226, б), поэтому в правой части уравнения (9.5) берется знак минус:

cPv _ М

dz* ~ ~ £■/•

ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ И ОПРЕДЕЛЕНИЕ ПОСТОЯННЫХ

|

Для того чтобы получить аналитическое выражение прогибов и углов поворота, необходимо найти решение дифференциального урав­нения (9.5).

Правая часть уравнения (9.5) является известной функцией от г, поэтому имеем простое дифференциальное уравнение. Интегрируя его первый раз, получим

Do , С М , ■. п , .

Это выражение определяет закон изменения углов поворота каса­тельной по длине балки. После повторного интегрирования находим уравнение оси изо­гнутого бруса: и = ± JJjg clzdz + Czi D. (б)

Г - '''I

<- - 24 •

Найденные значения постоянных подставим в уравнения (д) и (с) и получим уравнения прогибов и углов поворота:

EJm - EJ - - -^ql- - ^ql г² 4- -^- ■

£jy-t.J _dz- _{24 4} 2 -г g ,

F h) - ^ql3 z ^ql z^s 4- ^q-

Давая теперь абсциссе г определенные значения, получим числен­ные величины прогибов и углов поворота в определенных сечениях палки. Таким образом, можно вычислить прогиб и поворот сечения I! середине пролета, в четверти пролета и т. п.

Если в точке, где прогиб наибольший, функция прогибов имеет максимум, то для нахождения этой точки необходимо приравнять нулю первую производную от и, т. е. выражение для угла поворота. 15 данной задаче наибольший прогиб определяют из условия симмет­рии. Он находится посередине пролета. Положив г — 1/2, получим

5 ql* t'max - з8_{4 EJ}"•

Если на различных участках балки момент (или жесткость) имеет >азные законы изменения, то необходимо составить несколько диффе-

ii'lllMiankHUY VnaRHPUNM l^p5W.

те' из которых отвечает свое-

iy участку. В соответствии с ним число произвольных по-.тоянных равно удвоенному числу участков интегрирова­ния. Для определения посто­янных всегда можно устано­вить условия на границах каждого участка (граничные итювия). Так, например, из

i/ловий непрерывности и гладкости осп изогнутого бруса выте­кает, что на левом конце какого-либо участка прогиб и угол по­порота будут такими же, как на правом конце предшествующего участка.

Граничные условия приведут к системе уравнений, число которых соответствует числу постоянных. Совместное решение уравнений позволит найти постоянные и получить для каждого участка уравне­ние прогибов и углов поворота. Однако необходимость решения сов­местных уравнений очень сильно усложняет задачу, поэтому непо­средственное интегрирование применяют только в тех случаях, когда число участков невелико (однн-два).

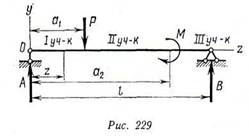
Рассмотрим балку, показанную на рис. 229. В данном случае имеем три участка, для которых изгибающие моменты равны:

Mi — Az, ОйСг^йь Ми — Az — р (z — a-i), a^-^z^a.,;

Мп1 = Лг —P(z-a₁) + Af, a_a«£z==s/.

]

Дифференциальные уравнения имеют вид: для первого участка

d-Vi Аг Ч& "^г EJ ' для второго участка

<Pv_u _Az-P(z-a_i)
dz¹ EJ '

для третьего участка

(&>Ш _ Аг-Р(г-_а1) + М
йг- EJ

Интегралы этих уравнений: для первого участка

•для второго участка

_А& Р(г-а^ ,_{r r}

для третьего участка

Az³ P tz о )■' Mz-

^yilI==bZf7" ы-j ' +2£Т + ^С'⁵² + ^С'⁶-

Для определения шести произвольных постоянных имеется шесть граничных условии: при г = 0 v (0) = 0; при г = щ прогибы и углы поворота для двух прилегающих участков одинаковы:

[Vl~Vu]z=_ai, йщ __ dv_u' _dz dzz = a,'

при z = а_г также имеют место равенства

[ОП = fill]* = o,i

I — и — ЁЕш]

ПрИ 2 = /

«111 (0 = 0.

Выполняя эти условия, получив шесть уравнений с шестью нешЯ вестными, которые необходимо совместно решить. Задача сильно усложняется, поэтому не будем доводить ее до конца.

В данном случае преследовалась цель показать методику и выяс­нить трудности, возникающие при решении задач, в которых балка ■агружена произвольной нагрузкой.

Для решения таких задач применяют другие методы, которые полагаются ниже.

МЕТОД НАЧАЛЬНЫХ ПАРАМЕТРОВ

• тому методу прогиб в лю- г'юм сечении балки опреде- 1яется через перемещения н силовые факторы, взятые и начале координат с… Представим себе, что

З - ei • а

М — функция,выражающая значение изгибающего момента в произвольном сечении первого участка. Разложимфункцию прогиба щ в ряд… у, = vi (0) + v (0) 2 + в," (0) | + v{" (0) {' + .... (б)

С

обращаются в нуль, поэтому получим тот же результат. Если в этой задаче положить q — О, то прогиб в балке от сосредоточенной силы б середине пролета (рис. 235, б) равен

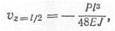
а угол поворота на опоре

 

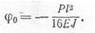
§ 80. МЕТОД МОРА ДЛЯ ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ

В предыдущих параграфах настоящей главы определялись пере­мещения в балках с прямой осью. Для брусьев с ломаной осью или' для системы, состоящей из нескольких стержней, применение описан­ных выше методов вызывает затруднения. Более универсальным яв­ляется метод Мора, который широко применяется в теории расчета стержневых систем. Этот метод основан на известном из теоретической механики принципе возможных перемещений.

Для удобства применения этого метода условимся относительно обозначений. Перемещение какой-либо точки по определенному на­правлению от какой-либо силы или группысил обозначается грече­ской буквой А, а перемещение от силы, равной единице, — буквой б. Кроме того, каждое из перемещений обозначается двумя значками, например А_КР, А_К1, б„„, и т. п. Первый значок обозначает точку, для^: которой определяется перемещение и вместе с'тем направление этого перемещения, а второй значок определяет причину, вызвавшую данное перемещение.

Так, например, А_КР может обозначать перемещение точки К по вертикали от группы сил Р. Если в какой-либо точке приложена сила Р_к по определенному направлению, то величину А_А-_Р можно рас­сматривать как перемещение по направлению силы Р_к от нагрузки, обозначаемой индексом Р.

Перемещение по направлению силы Р_к от температуры соответ­ственно следует обозначать Ад-,, второй значок / показывает, чтопричиной, вызвавшей перемещение, является температура.

Под обозначением Ь_тп нужно понимать перемещение по направле­нию воздействия т от /г-н единичной силы. Если перемещений

берется по направлению момента, то оно представляет собой угол поворота.

Такие обозначения обладают универсальностью, их можно пони-ч.пъ в обобщенном смысле не только как линейное или угловое, но ,i как групповое перемещение, например сближение каких-либо двух

1ОЧСК И Т. П.

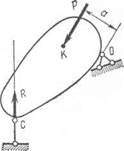
В теоретической механике начало возможных перемещений при­меняется к абсолютно жестким телам. По этому принципу в положе­нии равновесия работа всех сил на любых бесконечно малых возмож­ных (допускаемых связями) перемещениях равна нулю:

2Р_кЬ_Кя = 0, (9Л4)

, _лс Д_А-_Л _ составляющая возможного перемещения точки приложе-i и я силы Р_к по направлению этой силы от п -го возможного перемеще­ния системы.

 

Уравнение (9.14) применяется для исследования равновесия твер­дых тел, в частности для определения опорных реакций.

Для примера рассмотрим жесткий диск, показанный на рис. 243, а.

Поставим задачу определить опорную реакцию R. Разрежем опор-чый стержень и сообщим диску возможное бесконечно малое перемеще­ние. При этом диск повернется вокруг точки О на бесконечно малый , гол dq>. Точка К приложения силы Р переместится в точку К_ъ а точка С приложения реакции R переместится в точку С_х (рис. 243, б).

Перемещения точек приложения сил Р и R по направлению их действия от этого угла поворота составят:

Составляя уравнение принципа возможных перемещений, им€

 

Знак минус перед последним членом поставлен потому, что переме щение Ар_ф направлено в сторону, противоположную направлении действия силы Р.

Решая полученное уравнение относительно R, найдем

 

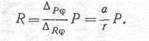
Точно такой же результат получится, если использовать обычное урав нение равновесия в виде

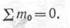
Рассмотрим теперь не абсолютно жесткое, а деформируемой упругое тело. Если задать точкам такого тела, находящегося; в равновесии, бесконечно малые перемещения, при которых появ-J ляются деформации, то в теле возникнут внутренние силы, которые! также произведут работу.

В этом случае уравнение принципа возможных перемещений (9.14); запишется так *:

V1 D Л _L_ Y7 _____ П /Q 1С I

Zi^K^aKn-r wкп — и. w-it>;.

Здесь первое слагаемое, так же как и в уравнении (9.14), представ-; ляет собой работу внешних сил на заданных возможных перемеще-, ниях, а второе слагаемое — работу внутренних сил также на возмож­ных перемещениях внутренних частиц тела.

Предположим, что при возможных перемещениях величина и, направление всех внешних и внутренних сил остаются неизменными, такими же, как в исходном состоянии, т. е., как обычно, ввиду ма­лости перемещений здесь не учитывается перераспределение усилий, связанное с деформацией тела.

Следовательно, в качестве возможных можно брать и конеч­ные, но малые перемещения, например определяемые на основе гипотез сопротивления материалов прогибы и углы поворота от какой-либо конкретной нагрузки.

Рассмотрим ломаный брус, показанный на рис. 244, а, под дейст-s вием силы Р_к = 1. В качестве возможных перемещений примем nepe-i мещения, которые произойдут вследствие деформации одного малого элемента длиной ds, расположенного в пределах, например, верти­кальной стойки (рис. 244, а). Предположим, что деформация эле-* мента ds произошла от какой-либо группы сил. При обозначении* внутренних сил и перемещений от этой нагрузки будем применять индекс Р. Так, например, внутренние силы в элементе ds от этой=; группы сил будут N_P, Мр и Q_P. Перемещение по направлению силы | Р_к = 1 (рис. 244, б) обозначим dA_KP. Оно равно проекции полного

I

перемещения точки К (отрезок K7Q на направление действия силы Р_к = 1.

Пользуясь формулой (9.15) для рассматриваемого случая, имеем

1 • d Акр -- dW кр = О, (9.16)

Здесь dW_KP — элементарная работа внутренних сил N_K, ~М_К и Q_K, вызванных силой Р_к = 1 на перемещениях (Ads)_P, dq>p и сдвигах у_Р, которые возникли вследствие деформации одного элемента ds. Эта деформация произошла от некоторой группы сил Р (на рис. 244 они не показаны). Черточка, проведенная над обозначениями N_K, M_K и Qk, показывает, что соответствующие значения найдены от единичной силы.

 

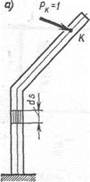
Общую деформацию элемента ds можно представить в виде трех составляющих: удлинения Ads_P (рис. 245, а), угла поворота сечения difp (рис. 245, б) и сдвигов каждого из волокон у_Р (рис. 245, в).

Внутренние силы, возникающие в элементе ds от силы Р_к = 1, являются по отношению к нему внешними силами. Нормальная сила ^!_к и момент Мц на перемещениях (Ads)_P и d<fp совершают работу, рав­ную (рис. 245)

Касательные напряжения распределены в сечении по сложному закону. Для определения работы сил x_KdF на перемещениях ypds составим интеграл-

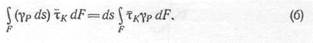
Складывая выражения (а) и (б), получим работу сил N_K и Мк и усилий, вызывающих сдвиги в элементе ds. Поскольку эти силы но отношению к элементу ds являются внешними, то работа внутрен­них сил будет иметь обратный знак. В силу сказанного второе сла-

 

гаемое, входящее в формулу (9.16), определяется равенством

 

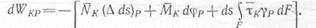
Подставляя это выражение в (9.16) и определив dA_KP, найдем

 

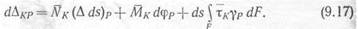
Вычислим вначале интеграл, входящий в формулу (9.17). Учтя,

 

 

 

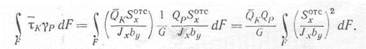
Обозначим, как это было сделано в § 67,

 

Эта величина является безразмерной идля каждого сечения может быть вычислена по формуле (9.18).

 

 

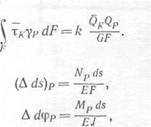
Подстановка дает

Учитывая далее, что

(9.19)

 

после подстановки этих выражений и выражения (9.19) в формулу (9.17) получим

Это перемещение возникает вследствие деформацийтолько одного малого элемента ds. Для учета деформаций всей системы в целом

необходимо проинтегрировать (9.20), распространяя интегрирование на все элементы системы. Принято такой интеграл снабжать индексом «s» внизу, который символизирует учет деформации всей системы в целом. Таким образом, имеем формулу Мора

 

Необходимо иметь в виду, что входящие в формулу Мора силовые факторы берутся в произвольной точке и поэтому представляют собой аналитические функции от координат произвольных точек.

Для шарнирно-стержневых систем, в которых стержни работают только на осевую силу, в формуле Мора (9.21) отличен от нуля только первый интеграл. В этом случае нормальная сила по длине каждого стержня обычно не меняет своей величины, поэтому подынтегральное выражение как постоянная величина выйдет за знак интеграла, а сам интеграл превратится в длину стержня. Учитывая деформацию всех стержней, получим

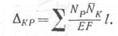
Так как рассматриваются только плоские стержневые системы, то значки у М, N, Q и / опускаем, т. е. считается, что М_я = М, Q_a = Q, /.v = / и т. п.

Остановимся теперь на технике вычисления интегралов Мора.

Заметим, что все три интеграла формулы Мора (9.21) имеют одина­ковый вид, который в общем виде можно представить так:

 

Предположим, что одна из подынтегральных функций является линейной функцией, а вторая, например f(s), — произвольной. На рис. 246 показан примерный вид функций f(s) и q(s).

Из рис. 246 видно, что

Подставляя эти выражения в интеграл (9.22), получим

 

Величина интеграла численно равна статическому моменту пло­щади Q эпюры f(s) относительно точки т (рис. 246), который в свою очередь равен площади всей эпюры, помноженной на отрезок s₀,

ПОЭТОМУ

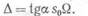
Но так как s_ntga = cp₀, где ср₀— ордината в эпюре <p(V), взятая иод центром тяжести площади Q, то

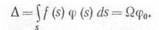
Таким образом, любой из интегралов Мора в пределах участка, на котором эти две эпюры непрерывны и одна из них линейная, равен площади криволинейной эпюры, помноженной на ординату линейной

Функция f(s)

 

эпюры, взятую под центром тяжести площади Q. Эпюры от единич­ных сил всегда линейные, поэтому ппи наличии нескольких участков

 

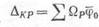
Полученное выражение носит название формулы Верещагина, автора данной формулы.

Если обе эпюры прямолинейные, то в любой из них можно брать площадь и в другой — ординату под центром тяжести первой эпюры.

 

Рассмотрим частный, но вместе с тем широко распространенны случай, когда на каком-то участке обе эпюры имеют вид трапецй (рис. 247).

В этом случае

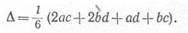
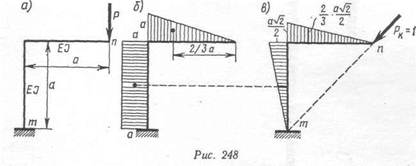
Пример 1. Определить, на сколько изменится расстояние между точками и я в результате деформации от изгиба рамы, показанной на рис. 248, а, пс

действием силы Р= Жесткости обоих стержней одинаковые и равны EJ. При опре­делении перемещений в рамах обычно пренебрегают влиянием нормальных и попе­речных сил и формулой Мора (9.21) учитывают только один интеграл, определя­ющий изгибные деформации:

 

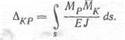
Здесь М_р — моменты от заданной нагрузки. Эпюра этих моментов показана на

рис. 248,6. Эпюру М_к строим от силы, приложенной в точке п по направлению к точке т (рис. 248,в).

Пользуясь формулой Верещагина, находим

Вычисления дают

 

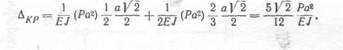
Глава XI СЛОЖНОЕ СОПРОТИВЛЕНИЕ

§ 88. ОБЩИЕ ПОНЯТИЯ

В предыдущих главах рассматривались задачи, в которых брус испытывал отдельно растяжение, сжатие, кручение или изгиб. На практике очень часто встречаются случаи, когда в результате дейст­вия нагрузки в поперечных сечениях бруса одновременно появляются несколько компонентов внутренних сил. Тогда говорят, что брус

находится в условиях с л о -

солротивле-

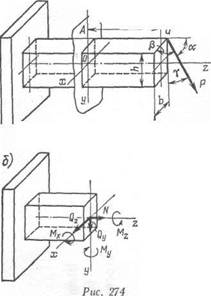
Ж II О Г О н и я. Рассмотрим действие си­лы Р в точке а, приложен­ной к брусу, заделанному одним концом (рис. 274, а). Проведем произвольное сече­ние плоскостью А и разме­стим в нем начало осей ко­ординат Охуг. Пусть направ-

4)

UJ.

Z

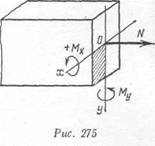
ляющие углы между силой Р и указанными осями координат соответственно будут а, у и р¹.

Нетрудно видеть, что от силы Р в произвольном сечении возникнут все шесть компонентов внутренних сил (рис. 274, б):

нормальная сила

N = Р cos а;

поперечные силы, направленные вдоль осей Оу и Ох:

Q_lt^P cosy; ^ч

изгибающие моменты:

 

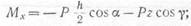
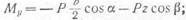
крутящий момент

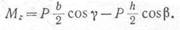
Нормальная сила и изгибающие моменты вызывают в точках поперечного сечения нормальные напряжения. От поперечных сили крутящего момента возникают касательные напряжения.

Для того чтобы определить суммарные напряжения, применяют принцип независимости действия сил, по которому, как известно, необходимо определить напряжения от каждого компонента внутренних сил в отдельности, а затем их сложить *. Для применения указан­ного метода прежде всего условимся относительно правила знаков.

Нормальную силу, как и прежде, будем считать положительной, если она в рассматриваемом сечении вызывает растягивающие напря­жения. Изгибающие моменты примем положительными, если они в точках, принадлежащих положительной четверти осей координат (совпадающих с главными осями), вызывают растягивающие напря­жения.

• На рис. 275 показаны оси координат Ох и Оу и им соответствую­щие положительные направления моментов М_х и М_у. На этом же рисунке показано положительное направление нормальной силы N. Все три указанных фактора вызывают в точках, лежащих в положи­тельной четверти, заштрихованной на чертеже, растягивающие напря­жения.

Так, при одновременном действии растяжения и изгиба в двух плоскостях нормальные напряжения в произвольной точке, лежащей в положительной четверти поперечного сечения бруса, определяют по формуле

N М_х М„

Г J д- J у

Среди случаев сложного сопротивления стержней особое место зани­мают наиболее часто встречающиеся сочетания отдельных простейших иидов нагружения,… Вместе с тем необходимо научиться определять внутренние сило-ные факторы для…

ПОСТРОЕНИЕ ЭПЮР ВНУТРЕННИХ УСИЛИЙ ДЛЯ СТЕРЖНЯ С ЛОМАНОЙ ОСЬЮ

Расчет таких стержней начи­нается с определения внутренних силовых факторов в ряде сечений. Для отыскания наиболее напря­женного (опасного) сечения… N, М,, Му, М„ Q.v, Qy. В первую очередь необходимо для каждого из стержней назначить

КОСОЙ ИЗГИБ

Так, например, обрешетины кровли (рис. 278) работают на косой изгиб. Вертикальная нагрузка от веса кровли и собственного веса обрешетин наклонена к… Собственный вес уголка, заделанного одним концом в стену (рис. 279), также… сечения уголка наклонены по отношению к нагрузке под некоторым углом.

ОДНОВРЕМЕННОЕ ДЕЙСТВИЕ ИЗГИБА И ПРОДОЛЬНОЙ СИЛЫ

о — ~у +-j~y. (11.8) Если нагрузка вызывает моменты относительно двух главных осей инерции (рис.… N My Mu <y = +T- + -7±y + -rLx. (П.9)

Gt; х J у

Если поперечное сечение стержня имеет простую форму, например прямоугольную, двутавровую и т. п., то для определения наибольшего напряжения следует… Р

ВНЕЦЕНТРЕННОЕ ДЕЙСТВИЕ ПРОДОЛЬНОЙ СИЛЫ

Предположим, что сжимающая сила Р приложена в точке с, кото­рая имеет координаты хР и уР, отсчитанные относительно главных центральных осей… От этой силы в произвольном сечении стержня возникают нормаль­ная сжимающая… в соответствии с принятым правилом знаков будут отрицательными, так как они вызывают сжатие в точках, лежащих в первой…

ЯДРО СЕЧЕНИЯ

бесконечности в направлении к центру тяжести сечения, оставаясь все время параллельной первоначальному своему положению. Наступит такой момент, когда нуле­вая линия в какой-либо точке коснется… две части: сжатую и растянутую. Таким образом, точка 1 является граничной точкой, за пределы которой нельзя перемещать…

ОДНОВРЕМЕННОЕ ДЕЙСТВИЕ КРУЧЕНИЯ С ИЗГИБОМ

вал имеет круглое сечение, у которого, как известно, все оси являются главными осями. В этом случае два изгибающих момента можно гео­метрически… Если определить суммарный момент в целом ряде точек и построить эпюру М„ для… Определив в расчетном сечении М„ и Мкр, можно установить, что

Глава XII ТЕОРИИ ПРОЧНОСТИ

ОСНОВНЫЕ ПОЛОЖЕНИЯ

В гл. III было установлено, что напряженное состояние в какой-чнбо точке тела полностью определяется одним главным напряжением при линейном… При возрастании действующей нагрузки главные напряжения бу­дут соответствующим… Для пластичного материала за предельное принимается такое напряженное состояние, при котором начинают развиваться…

ЭНЕРГЕТИЧЕСКАЯ ТЕОРИЯ ПРОЧНОСТИ

При построении данной теории первоначально была предложена гипотеза, согласно которой за причину наступления предельного напря­женного состояния… Условие, отвечающее такой гипотезе, записывается в следующем виде: U<U0, (12.11)

О + О2 /О —О 2

Для частного случая при оу = 0, положив az — а и хгу = т, имеем VW. (12.20) Энергетическая теория, так же как и третья, хорошо подтверждается в опытах с пластичными материалами и широко…

ТЕОРИЯ ПРОЧНОСТИ МОРА

В теории Мора в отличие от изложенных теорий не рассматриваются отдельные гипотезы, а на основе экспериментальных данных устанав­ливается… (рис. 302). Однако здесь на ос­нове имеющихся опытов не учи­тывают влияние… В случае, когда напряже­ния Qfj и а3 отвечают предель­ному напряженному состоянию главный круг принято называть

ОБЪЕДИНЕННАЯ ТЕОРИЯ ПРОЧНОСТИ

* Идея этой теории была высказана в 1936 г. проф. Н. Н. Давиденкоеым и в даль­нейшем развита Я. Б. Фридманом. Напряжение, при котором происходит отрыв, обозначим аотр, а напряжение,… Примером хрупкого разрушения может служить разрушение чугун­ного стержня при кручении, характерное отрывом,…

ПОНЯТИЕ 0 НОВЫХ ТЕОРИЯХ ПРОЧНОСТИ

Необходимо отметить, что помимо изложенных существует большое количество теорий, многие из которых не нашли достаточно широкого применения на… За последнее время появились новые теории, которые главным образом связаны с… При построении приведенных в предыдущих параграфах теорий составлялись условия наступления предельного напряженного…

.6

роение теории прочности для многих пластмасс осложняется тем, что их механические свой­ства оказываются нестабильны­ми. По сравнению с механиче­скими свойствами металлов свойства пластмасс в большой степени зависят от таких фак­торов, как время, температура и др.

Это обстоятельство заставля­ет обратить особое внимание на выбор необходимых величин ко­эффициентов запаса прочности.

В последнее время по тому же принципу, что и армирован­ные стекловолокнами пластмассы, создаются сверхпрочные металлы, у которых волокна в виде высокопрочных металлических нитевидных монокристаллов, или так называемых усов, помещаются в мягкой металлической матрице.

Такие материалы, обладая резко выраженными свойствами анизо­тропии, требуют разработки новых критериев прочности, учитывающих особенности их работы в условиях сложного напряженного состо­яния.

При построении новых теорий предельных напряженных состояний необходимо учитывать как недостатки имеющихся теорий, так и не­которые современные исследования и идеи, связанные с механизмом образования деформаций и проблемой разрушения твердых тел.

Одним из существенных недостатков имеющихся теорий является отсутствие необходимого объема экспериментальных данных, позво­ляющих надежно оценить достоверность той или иной теории в общем случае объемного напряженного⁴ состояния. Этот недостаток связан в основном с техническими трудностями постановки соответствующих опытов и поэтому в настоящее время применение существующих теорий

наиболее обосновано экспериментально лишь для плоского напряжен­ного состояния. Однако и в этом случае многие конструкционные материалы и особенно новые еще не достаточно исследованы на опыте.

Второй, также существенный недостаток имеющихся теорий заклю­чается в том, что при их построении материал рассматривается как сплошная однородная среда без учета его микроструктуры. Такая идеализированная модель материала оказывается удобной для построе­ния изложенной выше методики практических расчетов при сложном напряженном состоянии. Однако выполненные в последнее время экспериментальные' и теоретические исследования показали, что микроструктура реальных твердых тел оказывает большое влияние на их деформацию и разрушение. Пренебрежение этим влиянием неизбежно отражается на результатах расчета по той или иной теории прочности. Вместе с тем учет указанного влияния представляет весьма трудную задачу, решение которой должно было бы обеспечить практи­ческую возможность не только качественной, но и количественной оценки таких явлений, как пластическое деформирование, деформа­ционное упрочнение и разрушение того или иного материала, работаю­щего в условиях любого сложного напряженного состояния.

По пути к решению такой задачи на сегодняшний день пройдены хотя и важные по своему значению, но лишь первые шаги.

К недостаткам имеющихся теорий следует отнести и то, что соот­ветствующими критериями наступления предельного напряженного состояния материала не учитывается влияние таких факторов, как температура, время, а также масштабный фактор, устанавливающий зависимость величины используемых механических характеристик (предела текучести, предела прочности) от размеров рассчитываемого элемента конструкции.

Указанные выше основные недостатки имеющихся теорий ограни­чивают область их применения и во всех случаях делают необходи­мым учет приближенности получаемых с их помощью результатов, а также наличия экспериментальных данных, в достаточной степени подтверждающих ту или иную теорию. Одновременно следует отметить, что задача построения новых, а также усовершенствования имеющихся теорий прочности является на сегодняшний день весьма актуальной.

Глава XIII

ОСНОВЫ РАСЧЕТА ТОНКОСТЕННЫХ СТЕРЖНЕЙ ОТКРЫТОГО ПРОФИЛЯ

ОСНОВНЫЕ ПОНЯТИЯ

  Рис. 308

СВОБОДНОЕ КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ

Так, на рис. 310, а, б показан стержень, нагруженный на концах моментами и работающий в условиях свободного кручения. В таком стержне расстояние… лежащими на любой образующей, до и после деформации остается неизменным. Отсюда вытекает, что на любом участке стержня все продольные волокна сохраняют свою первона­чальную длину, их…

Т - М" А /пи

d В формулах (13.1) и (13.2) обозначены: Мо — момент чистого кручения; б —… J d — геометрическая характеристика сечения, выполняющая ту же роль, что и полярный момент инерции для стержней с…

Глава XIV РАСЧЕТ КРИВОГО БРУСА

ОБЩИЕ ЗАМЕЧАНИЯ

  показаны примеры кривых брусьев: крюк подъемного крана, замкну­тое кольцо,… В дальнейшем ограничимся рас­смотрением таких плоских кривых брусьев, которые имеют симметрич­ные поперечные сечения,…

РАСТЯЖЕНИЕ И СЖАТИЕ КРИВОГО БРУСА

В условиях центрального растяжения (сжатия) работает круговой стержень под дейст- вием равномерной радиальной нагрузки и продольных сил, прило­женных на торце (рис. 342).

ЧИСТЫЙ ИЗГИБ КРИВОГО БРУСА

На рис. 344, а, б показан элемент бруса длиной ds с симметричным поперечным сечением. Ось Ох направим по нейтральной оси, вокруг которой… Эпюра абсолютных удлинений волокон показана на рис. 344, в, а эпюра… Абсолютное удлинение на высоте сечения изменяется по закону прямой линии, а относительное — по закону кривой линии…

ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ НЕЙТРАЛЬНОЙ ОСИ В КРИВОМ БРУСЕ ПРИ ЧИСТОМ ИЗГИБЕ

При точном решении задачи необходимо исходить из условия (14.2). Для каждого типа поперечного сечения получится свое…

НАПРЯЖЕНИЕ ПРИ ОДНОВРЕМЕННОМ ДЕЙСТВИИ ПРОДОЛЬНОЙ СИЛЫ И ИЗГИБАЮЩЕГО МОМЕНТА

В этой формуле величина изгибающего момента должна быть . найдена относительно оси, проходящей через центр тяжести сечения,

Т F *? "л 99 R f Q ft " Ч

Интересно сравнить полученные результаты с теми, которые будут определены по обычным формулам для прямого бруса. Момент инерции сечения…   Эти цифры убедительно показывают, что для расчета кривых бру­сьев, вообще говоря, нельзя пользоваться формулами,…

Глава XV УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ

§ 115. ОСНОВНЫЕ ПОНЯТИЯ

В предыдущих главах рассматривались методы определения па-пряжений и деформаций при растяжен-:и, сжатии, крученияи изгибе. Были также установлены критерии прочности материала при сложном сопротивлении.

Однако во многих случаях проектирования инженерных сооруже­ний обычных расчетов на прочность бывает недостаточно для того, чтобы получить полное представление о работе сооружения.

Выяснение того, что напряжения не превосходят расчетного со­противления материала, не дает еще трава сделать вывод о безопас­ности существования сооружения.

Наряду с проблемой прочности существует проблема так называе­мой устойчивости сооружения или егэ элементов.

Инженерные объекты помимо . нагрузок, учитываемых расчетом, всегда подвергаются дополнительным малым воздействиям (возмущениям), стремящимся вывести данное тело из егорасчетного состояния равновесия и.:и движения.

Если малые возмущения вызовут ж-лые отклонения системы от расчетного (невозмущенного) состояния, то это состояние системы является устойчи­вым. Наоборот, если при малых возме­щениях возникнут большие отклонениясистемы от расчетного со­стояния, то последнее является неусп. йчивым.

Наглядным примером устойчивогоили неустойчивого состояния может служить вращение обычного волчка (гироскоп). Хорошо из­вестно, что чем больше скорость вращения волчка, тем большее со­противление он оказывает попыткам отклонить его от вращения вокруг вертикальной оси. Таким образом, вращательноедвижение волчка при больших скоростях по отношению к малым возмущениям устой­чиво. При уменьшении скорости вращения ниже некоторого значения те же малые возмущения резко изменят его состояние и вызовут беспорядочные движения. Таким образом, при малых скоростях вра­щения движение волчка становится неустойчивым.

Примером устойчивого или неустойчивого равновесия является равновесие тяжелого шарика, лежащего в вогнутой или на выпуклой сфере (рис. 350). В первом случае (рис. 350, а) при любом малом отклонении шарик стремится вернуться в исходное состояние. Исход­ное и отклоненное состояния шарика мало отличаются друг от друга. Во втором случае (рис. 350, б) при любом малом отклонении шарик

покатится вниз. Возмущенное изаданное состояние шарика резко отличаются друг от друга.

Шарик, лежащий на дне вогнутой сферы, находится в устойчивом равновесии, а на вершине выпуклой сферы его равновесие неустой­чиво.

Аналогичные явления можно наблюдать при изучении равновесия сжатого стержня. При малой сжимающей силе, меньшей некоторого критического значения Р «< Р_кр, сжатый стержень нечувствителен к малым возмущениям. Незначительные дополнительные воздействия мало отклоняют стержень от его прямолинейного состояния. При Р > Р_кр прямолинейная форма сжатого стержня неустойчива. Сколь угодно малые случайные воздействия вызовут большие отклонения. Стержень после устранения возмущений останется в изогнутом со­стоянии под действием продольной силы. Такое состояние называют продольным изгибом.

Появление продольного изгиба опасно тем, что при нем проис­ходит очень сильное нарастание прогибов при малом нарастании сжимающей силы. Прогибы и нагрузка связаны междусобой нелиней­ной зависимостью. Быстрое нарастание прогибов вызывает быстрое нарастание напряжений от изгиба, которые в свою очередь приводят к ускорению деформаций и часто к разрушению стержня.

Для тонких (гибких) стержней потеря устойчивости часто насту­пает при сравнительно небольших сжимающих напряжениях, не являющихся опасными с точки зрения прочности самого материала.

История развития строительного искусства знает немало случаев крушения инженерных сооружений из-за неправильного их расчета на устойчивость. Так, например, в 1907 г. обрушилсябольшой мост консольной системы с главным пролетом 549 м через реку Св. Лаврен­тия в США. Разрушение произошло во время строительства за 15 мин до конца рабочего дня, при этом все находившиеся на мосту рабочие итехники погибли (всего погибло 74 человека); 9 тыс. т металличе­ских конструкций пришло в полную негодность. Большая часть кон­струкций затонула в воде, погрузившись в отдельных местах на глу­бину более 40 м.

Это грандиозное крушение Квебекского моста (мост строился в 14 км от Квебека) весьма поучительно. Причиной катастрофы явился неправильный расчет сжатого составного стержня на устойчивость.

В то время теория расчета таких стержней не была в достаточной степени разработана, что является извиняющим обстоятельством для проектировщиков.

Интересно отметить, что спустя 9 лет, когда в 191G г. завершились работы по возведению нового Квебекского моста на том же месте и по той же схеме, произошло вторичное крушение, при котором упал в воду и затонул подвесной пролет.

Другой трагический случай, который может служить предметным уроком, доказывающим необходимость и важность тщательного рас­чета сжатых элементов на устойчивость, произошел смостом у деревни Менхенштейн в Швейцариив мае 1891 г. В момент катастрофы по мосту проходил пассажирский поезд, состоявший из 12 вагонов. Мост

имел небольшую длину — всего 42 м. Паровоз успел пройти через мост, но упавшие вагоны увлекли его за собой. Из 12 вагонов упало 6; падавшие друг на друга вагоны разбивались и образовывали груду обломков. При катастрофе погибло 74 и было ранено около 200 чело­век. Причина катастрофы заключалась в том, что один из сжатых рас-

р>р„,

 

косов фермы потерял устойчивость и повлек за собой разрушение всего моста.

Таким образом, продольный изгиб является опасным, его допускать нельзя. Поперечные сечения сжатых стержней должны назначаться не из условий прочности от чистого сжатия, а из условий того, чтобы сжимающие напряжения были меньше критических напряжений:

_p V

Определение критических сил, изучение форм потери устойчиво­сти, разработка метода подбора сечений составляют основную задачу науки об устойчивости сооружений.

На рис. 351 показаны случаи потери устойчивости различных упругих систем. В сжатом стержне (рис. 351, о) при превышении силой критического значения может произойти выпучивание. Сжи-

 

мающая сила вызывает, кроме сжатия, также изгибающие моменты. Кольцо (рис. 351, б) под гидростатическим давлением во всех сечениях испытывает центральное сжатие. Однако при некотором значении давления q> q_HV круговое очертание кольца перестает быть устойчи­вым. Кольцо изгибается н превращается в эллипс.

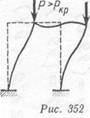
На рис. 352 показана рама, на которую действуют силы, приложен­ные в узлах. Эти силы вызывают центральное сжатие в стойках.

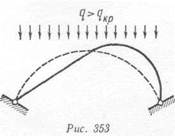
Как только силы Р превысят критическое значение, рама мгновенно изогнется, узлы ее переместятся в сторону, произойдет потеря устой­чивости первоначально заданного равновесия рамы. Такая же картина происходит с аркой (рис. 353).

Все изображенные на рис. 351—353 случаи характерны тем, что до потери устойчивости во всех сечениях наблюдалось только цент­ральное сжатие. В момент потери устойчивости к центральному сжа­тию присоединяется изгиб. Система переходит из одного состояния равновесия в другое. Происходит потеря устойчивости центрального сжатия.

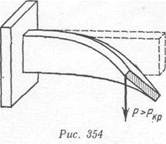
На рис. 354 показан другой случай потери устойчивости. Вначале балка испытывает изгиб в вертикальной плоскости (плоский изгиб). Как только сила превысит критическое значение, плоская форма изгиба становится неустойчивой, появляются допол­нительный изгиб в горизонтальной плоскости и кру­чение. Аналогичным образом может произойти потеря устойчивости при кручении, внецентренном сжатии и при других видах деформации.

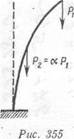
Если система загружена не одной, а несколь­кими силами или какой-либо сложной нагрузкой, то выбирается один параметр и вся система сил считается изменяющейся пропорционально этому параметру. Например, для стержня, загруженного двумя силами (рис. 355), сила Р₂ выражена через Р₁ (Р₂ = аР_у) с помощью множителя а. Таким об­разом, P_i принимается за параметр, с точностью до которого заданы все силы. Определив критический параметр Р_1кр и зная а, можно найти всю критическую нагрузку для такого стержня.

Вопросами устойчивости занимается специальная наука — «устой­чивость сооружений». В курсе сопротивления материалов обычно рассматривается только одна наиболее простая задача об устойчивости прямолинейных сжатых стержней, представляющая собой как бы введение в общую теорию устойчивости сооружений. Этим вопросам и посвящается данная глава.

МЕТОД ЭЙЛЕРА ДЛЯ ОПРЕДЕЛЕНИЯ КРИТИЧЕСКИХ СИЛ. ВЫВОД ФОРМУЛЫ ЭЙЛЕРА

Наиболее универсальным является динамический метод, основан­ный на изучении колебаний системы вблизи заданного положения равновесия. Однако в курсах… в инженерной практике, может быть решено более простым методом — методом… Метод Эйлера основан на анализе разветвления возможных форм равновесия упругой системы. Рассмотрим его идею более…

ВЛИЯНИЕ СПОСОБОВ ЗАКРЕПЛЕНИЯ КОНЦОВ

СТЕРЖНЯ НА ВЕЛИЧИНУ КРИТИЧЕСКОЙ СИЛЫ

случаев, изображенных на рис. 358, критическую силу можно опре­делять по обобщенной формуле (15.7)