Кинематика поступательного движения.
Поступательным называется движение твердого тела, в котором произвольная прямая, жестко связанная с телом, остается параллельной самой себе в процессе движения.
Линию, которую описывает произвольная точка тела в процессе движения, называют траекторией движения. В поступательном движении траектории движение всех точек тела одинаковые, поэтому достаточно изучить движение одной точки и движение всего тела будет изучено. Моделью для изучения поступательного движения принимается материальная точка - это тело, размеры которого не существенные в постановке конкретной задачи. Материальная точка имеет массу тела. Графически изображается, как и в математике: „×”. Ее положение в пространстве может быть задано (рис. 5.1) тройкой координат x, в, z (координатный способ); с помощью радиус-вектора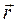 
(векторный способ); длиной отрезка траектории (путь S), если траектория известна (естественной способ) (см. рис. 5.1 а); если точка движется по окружности, то все эти методы могут быть использованными и очень полезным может быть задание радиус-вектора в полярных координатах 
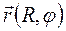, то есть радиусом окружности R и углом j его наклона к определенному направлению (рис. 5.1 б).
Основная задача механики в переводе на язык математики сводится к построению функций:
x=x(t), у=у(t), z=z(t),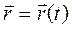 
, S=S(t), j=j(t). (1.1)
Решается такая задача, как это принято в науке, путем дифференцирования характеристик положения тел с последующим интегрированием и поиском первообразных функций (1.1).
На этом пути вводятся кинематические характеристики: первая производная – скорость и вторая производная – ускорение, которая являются скоростью изменения скорости. Как это известно из динамики, ускорение движения тела находится по силам, действующим на тело, поэтому третью и другие производные вводить нет необходимости. Известные выражения первой, или второй производных это дифференциальные уравнения, решение которых дает возможность найти первообразную функцию и дать ответ на основную задачу механики, то есть построить функции (1.1).
Рассмотрим особенности решения задачи механики разными методами. Начнем с наиболее общего инвариантного, то есть независимого от выбора конкретной системы координат, векторного способа.
Векторный способ. Положение точки в пространстве задается с помощью радиус-вектора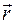 
, то есть вектора, определяющего положение точки относительно какого-то полюса, например начала координат О (см. рис. 5.1). Способ требует построения функции 
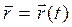, или, так как
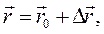где 
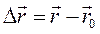(1.2)
перемещение точки (см. рис. 5.1 а), функции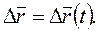 
Скорость при векторном способе называется скоростью движения, либо скоростью перемещения и равняется первой производной от радиус-вектора, либо от перемещения точки по времени:
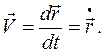(1.3)
Скорость перемещения – величина векторная и направлена по касательной 
к траектории в сторону направления движения точки (см. рис. 5.2 а), как и бесконечно малое перемещение: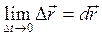 
.
Ускорение (ускорение движения или ускорение перемещения точки) – это скорость изменения скорости и первая производная от скорости по времени или вторая производная от радиус-вектора или перемещения:
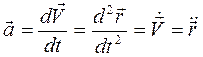. (1.4)
Ускорение движения или ускорение перемещения является величиной векторной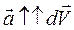 
. В общем случае 
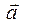направлено в сторону вогнутости траектории (рис. 5.2 б), имеет размерность 
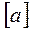=м/с2.
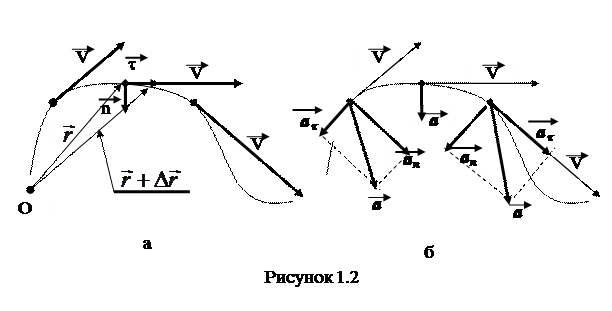
Ускорение движения материальной точки может быть представленным в виде суммы двух составляющих аt и аn (см. рис. 5.2 б), физическое содержание которых можно понять если найти производную от скорости движения, представленной как произведение ее модуля V на единичный вектор касательной к траектории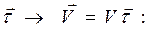 
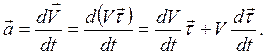(1.5)
Из курса математики известно, что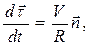 
где 
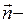единичный вектор внутренней нормали к траектории движения, а R – радиус ее кривизны в исследуемой точке. Подставив полученное выражение в формулу (1.5) получим
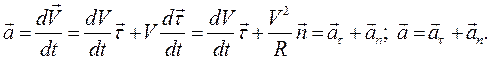(1.6)
По смыслу, как это следует из анализа выражений (1.5) и (1.6), тангенциальное ускорение характеризует скорость изменения скорости по модулю, а нормальное ускорение характеризует скорость изменения направления скорости. Тангенциальное ускорение 
направлено по касательной к траектории движения точки или в сторону движения, если скорость растет, или антипараллельно скорости, если скорость уменьшается (см. рис. 5.2 б). Нормальное ускорение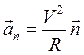 
направлено по внутренней нормали к центру кривизны траектории. Численное значение ускорения
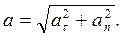(1.7)
Тангенциальное и нормальное ускорение могут быть признаками разных движений:
1) 
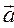= const – равнопеременное движение;
2) аn = 0 прямолинейное движение;
3) 
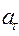= 0,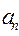 
¹ 0 – равномерное криволинейное движение;
4) 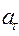=0, 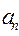=const – равномерное движение по окружности.
Координатный способ требует построения функций x=x(t), у=у(t), z=z(t). Соответственно в координатном способе изучения вводятся скорости координат как первые производные от соответствующих координат:
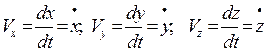(1.8)
и ускорение координат, которые характеризуют скорость изменения скорости соответствующих координат точки:
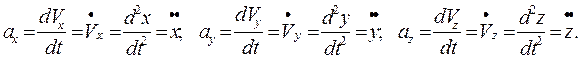(1.9)
Введенные величин скорости и ускорения координат сугубо скалярные. Могут быть положительными, отрицательными или нулями в зависимости от того, растут или уменьшаются или остаются неизменными во времени координаты или скорости координат.
Естественный способ используется в том случае, когда траектория движения известна, то есть в каждой ее точке являются известными единичные векторы касательной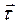 
, внутренней нормали 
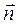(для пространственной кривой также внутренней бинормали 
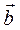) и радиус кривизны траектории R. Соответствующие кинематические характеристики: путь S – как длина отрезка траектории, пройденной точкой; путевые скорость и ускорение, является величинами сугубо скалярными положительными. Для ответа на основную задачу механики необходимо построить функцию S=S(t).
Путевая скорость вычисляется, как первая производная от пути:
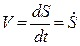, размерность 
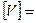м/с. (1.10)
Путевое ускорение:
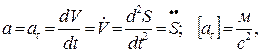. (1.11)
В естественном способе изучения движения практический смысл имеют средние скорость и ускорение:
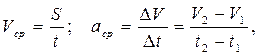(1.12)
то есть средняя путевая скорость движения равняется отношения пути, пройденного телом, ко времени движения, а среднее значение ускорения равняется отношению изменения путевой скорости к промежутку времени, за которое это изменение состоялось.
Изучение движения материальной точки по окружности, как это было указано выше, полезно провести в представлении радиус-вектора в полярных координатах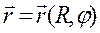 
(см. рис. 5.2 б). Потому что R, как радиус окружности, остается неизменным на протяжении всего движения, поиск функции 
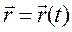сводится к поиску зависимости j = j(t). С этой целью вводятся угловые характеристики.
Угол поворота радиус-вектора j и его дифференциал dj есть величины скалярные (хотя могут считаться аксиальными векторами), поэтому и угловая скорость и угловое ускорение вращения радиус-вектора исследуемой точки также величины скалярные.
Угловая скорость
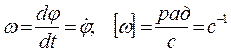(1.13)
(
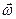может считаться аксиальным вектором как и дифференциал угла поворота).
Угловое ускорение – это первая производная от угловой скорости или вторая производная от угла поворота. За единицу углового ускорения принято рад/с2.
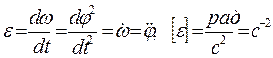(1.14)
(
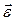может считаться аксиальным вектором как и угловая скорость и дифференциал угла поворота).
Связь между характеристиками движения в разных способах представления
Координатный способ
По определению радиус-вектор имеет своими проекциями координаты исследуемой точки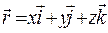 
-, где 
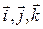- единичные векторы, соответствующих координатных осей. Если взять производную по времени от левой и правой частей, равенство не нарушится:
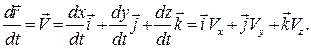(1.15)
Но вектор скорости в проекциях на оси координат имеет вид
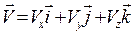, (1.16)
поэтому, сопоставив выражения (1.16) и (1.15), имеем вывод, проекции скорости совпадают со скоростями соответствующих координат:
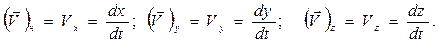(1.17)
Модуль скорости
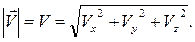(1.18)
Соответственно для ускорения:
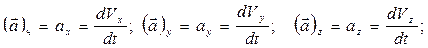(1.19)
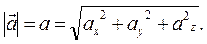(1.20)
Естественной способ и движение точки по окружности.
По определению путевая скорость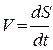 
,ибесконечно малая дуга 
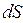совпадает с соответствующей ей хордой 
: 
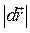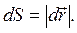Поэтому
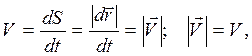, (1.21)
то есть модуль скорости равняется путевой скорости. Кроме того, как это было записано выше,
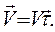(1.22)
В движении по окружности путь, пройденный точкой, то есть дуга окружности, выражается через радиус и центральный угол (см. рис. 5.1 бы):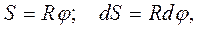 
поэтому связь между линейными и угловыми характеристиками такая:
. (1.23)
В практических исследованиях движение точки по окружности выражают в числе оборотов N и скорость движения точки по окружности
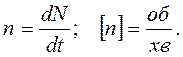(1.24)
Ввиду того, что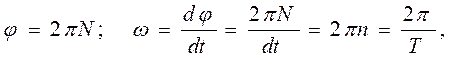 
где Т – период обращения точки по окружности. Таким образом
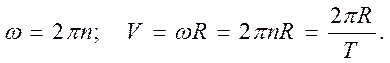(1.25)
Для ускорения и его составляющих, ввиду приведенных выше связок имеем:
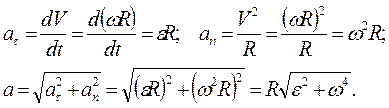(1.26)