См. (И1),(И2) в лекции №11
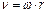 Предадим векторный вид
Предадим векторный вид 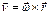 Введем радиус вектор мт… и учтем что
Введем радиус вектор мт… и учтем что 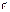 направлена по касательной окружности. По построению видно, что
направлена по касательной окружности. По построению видно, что 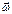 перпендикулярна плоскости окружности.
перпендикулярна плоскости окружности.
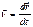
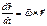
Описываем изменение во времени 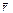 при условии что его модуль const, а конец движ. со скоростью
при условии что его модуль const, а конец движ. со скоростью 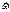 .
.
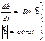
см(И3) в лекции№11
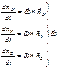
Мы переходим к случаю когда сист. отсчета НСО движется произвольно ИСО.
В общем случае это движение можно разложить на 2 состав. Первое это пост. и ускор. движ центра О-
этот случай мы рассмотрели ранее. Второе это вращательное движение сист. XOYZ с углов. скор. 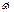 с
с
углов. ускор. 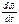 ;
; 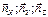 -единые орты НСО.
-единые орты НСО.
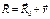 Продеференцируем по времени, один раз
Продеференцируем по времени, один раз 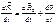
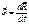 -это скорость мт в НСО.
-это скорость мт в НСО. 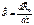 -это скорость в точке О в НСО.
-это скорость в точке О в НСО.
Найдем 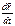 с учетом разложения
с учетом разложения 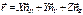 , а так же учитывая то что орты вращаются с
, а так же учитывая то что орты вращаются с
угловой скоростью 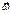 .
.
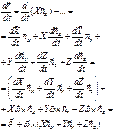
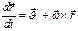 ;
; 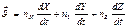
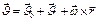 ;
; 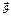 -скорость мт в НСО,
-скорость мт в НСО, 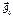 - скорость нач. координат в НСО,
- скорость нач. координат в НСО, 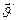 -скорость Мт в НСО,
-скорость Мт в НСО, 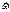 - угловая скорость вращения.
- угловая скорость вращения.
№24. Общий случай движения НСО: ускорение.
Продеференцируем обе части 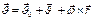 ( Общий случай движения НСО: скорость.) по времени
( Общий случай движения НСО: скорость.) по времени
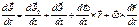
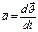 -ускорение Мт в НСО;
-ускорение Мт в НСО; 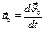 -ускорение т. О в НСО;
-ускорение т. О в НСО;
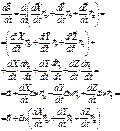
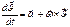 ;
; 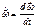 ;
; 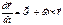 ;
;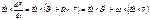
Подставим преобразования:
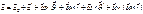
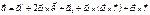 Является окончательной формулой и дает связь между
Является окончательной формулой и дает связь между 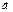 и
и 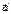 для произвольного движения НСО.
для произвольного движения НСО.
Вектор 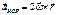 - Кориолисово ускорение.
- Кориолисово ускорение.
Введем вектор 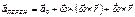 - это вектор назыв. переносным ускорением, именно такое ускор. в НСО имеет Мт, которое покоится.
- это вектор назыв. переносным ускорением, именно такое ускор. в НСО имеет Мт, которое покоится.
№25.Уравнение динами Мт в НСО.
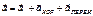 ;
; 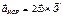 ;
;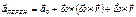 ;
;
Применим 2 з. Ньютона для ИСО в S1: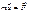 ;
; 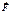 -настоящая сила.
-настоящая сила.
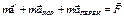 ;
;
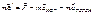 ; -Это уравнение представляет собой основной закон динамики в НСО, для общего случая поступательного и вращательного ускоренного движения относительно ИСО
; -Это уравнение представляет собой основной закон динамики в НСО, для общего случая поступательного и вращательного ускоренного движения относительно ИСО
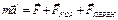
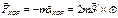 -Кореолесова сила инерции.
-Кореолесова сила инерции. 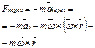
Первое слагаемое в 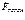 с ускорением поступательного движения системы S. Основные 2 слагаемых возникают из-за ,вращательного движения НСО, с угловой скоростью
с ускорением поступательного движения системы S. Основные 2 слагаемых возникают из-за ,вращательного движения НСО, с угловой скоростью 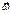 и угловым ускорением
и угловым ускорением 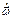 .
.
Кореолесова сила определяется с одной стороны вращением НСО, а с другой скоростью Мт относительно S.
№26. Движение Мт относительно вращающейся Земли.
Рассмотрим S1 связанная с солнцем приблизительно инерциальна, система S связана с Землей, суточное вращение. Внешнюю реальную силу(результирующую).
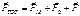 ;
;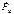 -сила притяжения Земли.
-сила притяжения Земли. 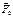 -сила притяжения со стороны солнца.
-сила притяжения со стороны солнца.
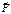 - результирующая всех других сил.
- результирующая всех других сил.
Тогда закон механики 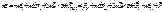
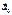 -ускорения центра Земли под действием гравитации солнца.
-ускорения центра Земли под действием гравитации солнца.
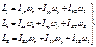 ;
; 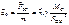 ;
;
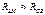
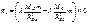 .
.
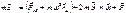 . (1)
. (1)
По определению вектор 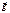 определяемый из равенства
определяемый из равенства 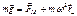 называется вектором свободного падения.
называется вектором свободного падения.
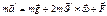 (2)
(2)
Формулы (1) и (2) совместно являются уравнениями движения Мт.
№27. Вес тела. Маятник Фуко.
Весом тела называют силу 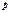 приложенную к телу!!! Которая равна и противоположно направлена силе, с которой подставка действует на тело!
приложенную к телу!!! Которая равна и противоположно направлена силе, с которой подставка действует на тело!
При этом мы считаем, что тело покоится относительно Земли (НСО).
Применим формулу 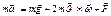 ,
,
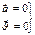
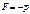
подставим
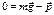 ;
;
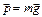 . (1)
. (1)
С учетом того, что 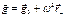 мы видим, что вес тела состоит из 2 частей:
мы видим, что вес тела состоит из 2 частей:
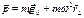 (2)
(2)
согласно этой формуле вес тела есть векторная сумма силы гравитационного притяжения Земли 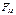 и центробежной силы инерции.
и центробежной силы инерции.
Фор-лы (1) и (2) есть конечные формулы вопроса (вес тела).
Пусть пл-сть колеб. совпадает с пл-ю рисунка.
Маятник имеет скорость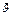 ,
,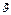 -начальная к траектории
-начальная к траектории
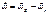
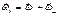
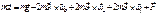 ;
;
1) 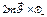 -это состав. действ. вдоль нити, растягивающая ее.
-это состав. действ. вдоль нити, растягивающая ее.
2)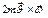 -сила мала и она оказывает малое влияние, т. к.
-сила мала и она оказывает малое влияние, т. к. 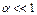 .
.
3) 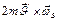
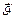 и
и 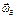 находятся в пл-ти доски. Эта сила
находятся в пл-ти доски. Эта сила 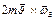 направлена перпендикулярно доске, является частью силы Кориолиса и вызывает смещение пл-ти колебаний, и в результате это смещение становится заметным.
направлена перпендикулярно доске, является частью силы Кориолиса и вызывает смещение пл-ти колебаний, и в результате это смещение становится заметным.
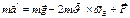
№28.Углы Эйлера.
Углы Эйлера -3 угла, которые описывают вращение системы S с тт. относительно S1.
Рис.1: 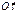 -прямая по которой пересекаются плоскости
-прямая по которой пересекаются плоскости 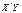 и
и 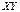 .
.
Дадим ряд определений:
Пл-ть 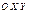 пересекает пл-ть OXY по линии
пересекает пл-ть OXY по линии 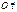 (линия узлов), полож. направление совпадает с вектором
(линия узлов), полож. направление совпадает с вектором 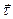 .
. 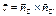 .
.
По определению углы Эйлера называются углы: 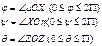
Угол 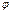 является углом собственного вращения.
является углом собственного вращения.
Угол 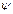 называется углом процессии.
называется углом процессии.
Угол 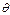 называется углом нутации.
называется углом нутации.
№29.Вращательное движение.
Вращательное движение, при котором 2 его точки остаются всегда неподвижными, прямая проходящая через эти точки - называется осью вращения.
Все остальные точки не лежащие на оси описывают окружности в плоскостях оси вращения, центры этих окружностей лежат на оси вращения.
Рассмотрим какую либо точку, которая движ. по окружности. R-радиус, 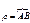 .
.
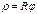
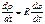 ;
; 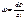 -угловая скорость вращения тт.
-угловая скорость вращения тт.
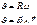
№30.Уровнение движения твердого тела.
Мы говорили о том, что тт. есть СМТ мы доказали, что эта система обладает 6 степенями свободы, поэтому для описания СМТ необходимо 6 скалярных уравнений; 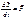 ;
; 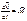 ;
;
Эти уравнения есть уравнения описывающие динамику тт. – это 6 скаляр. уравнений
Уравнения моментов можно брать относительно произвольного неподвижного начала или относительно центра масс тт.. Можно также брать произвольно движ. начало, если только скорость его в любой момент времени параллельна скорости центра масс. При ограничение свободы движ. число независимых уравнений, требующихся для описания движ. тт. , уменьшается. Она всегда равна числу степеней свободы.
Внутренние силы не влияют на движ. тт.
 №31.Моменты инерции.
№31.Моменты инерции.
(см. и5 лекции 14)
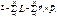
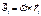 (1)
(1)
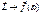
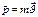 (2)
(2)
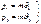 (3)
(3)
представим, что 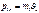
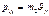 ,
,
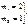 (4)
(4)
(не такая экзотика для полупроводников)
вывод: если между проекциями физ. Величин сущ-ет связь типа (4), причем 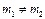 , то видим, что векторы, для которых эта связь справедлива, непараллельны
, то видим, что векторы, для которых эта связь справедлива, непараллельны
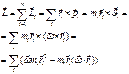
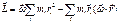 (5)
(5)
Формула (5) уже дает связь между 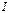 и
и 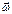 , но она достаточно неявна. Преобразуем (5), для этого рассмотрим проекции
, но она достаточно неявна. Преобразуем (5), для этого рассмотрим проекции 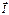 на оси координат.
на оси координат.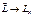 ,
, 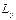
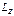
1)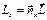
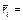 (
(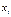 ;
;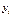 ;
;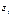 )
)
(6)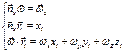
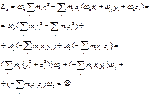
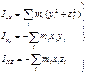 (7)
(7)
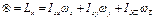 (8)
(8)
Формула (8) дает связь проекции 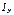 момента кол-ва движения ТТ и сразу с тремя проекциями вектора угловой скорости
момента кол-ва движения ТТ и сразу с тремя проекциями вектора угловой скорости 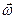
Аналогично получим:
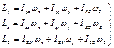 (9)
(9)
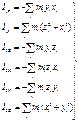 (10) Из формул (10) видно:
(10) Из формул (10) видно: 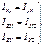 (11)
(11)
Из 9-ти коэффициентов независимы только 6.
Величины 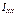 ,
, 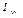 ,
, 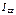 называются
называются
осевыми моментами инерции тв. тела.
Величины 
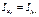 ,
, 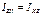 ,
, 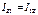
называются центробежными моментами инерции ТТ.
Величины 
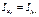 ,
, 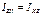 ,
, 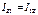
называются центробежными моментами инерции ТТ.
Векторы 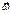 и
и 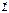 не параллельны. Такая связь, когда связываются 2 не параллельных вектора называется тензорной связью, и говорят, что эта связь определяется с помощью тензора 2-го ранга.
не параллельны. Такая связь, когда связываются 2 не параллельных вектора называется тензорной связью, и говорят, что эта связь определяется с помощью тензора 2-го ранга.
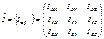 (12)
(12)
Тензор 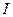 , введенный в формуле (12) с помощью (10) называется тензором инерции твердого тела.
, введенный в формуле (12) с помощью (10) называется тензором инерции твердого тела.
Величины 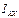 ,
, 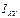 и т.д., называются компонентами тензора.
и т.д., называются компонентами тензора.
Тензор 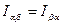 называется симметричным тензором.
называется симметричным тензором.
№32.Вычисление моментов инерции относительно оси.
Пусть ось Z есть ось вращения.
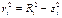
 (1)
(1)
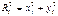 (2)
(2)
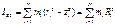 (3)
(3)
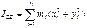 (4)
(4)
Момент инерции относительно оси.
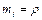 (
( 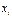 ;
; 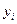 ;
; 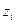 )
)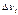
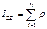 (
(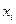 ;
; 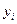 ;
;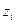 )
)
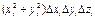
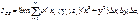
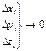
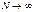
Этот предел если существует, то равен объемному интегралу
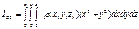 (5)
(5)
Формула (5) дает выражение для момента инерции относительно оси в случае непрерывного
расположения массы вещества.
 №33.Теорема Гюйгенса-Штейнера
№33.Теорема Гюйгенса-Штейнера
(см. рис в лекции №17)
Расм. произвольное тв. тело. Пусть точка О –центр масс этого тела, а ось 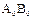 проходит через центр масс. Пусть АВ – ось //
проходит через центр масс. Пусть АВ – ось // 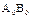 и нах-ся на расстоянии а. пусть Ri- радиус i-той точки, лежащей в пл-сти xoy.
и нах-ся на расстоянии а. пусть Ri- радиус i-той точки, лежащей в пл-сти xoy.
Ri отсчитывается от центра масс. 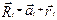 (1)
(1)
Задача: сравнить осевой момент инерции относительно оси 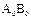 и оси АВ
и оси АВ

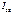 от
от 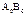
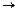 Iо
Iо

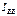 от АВ
от АВ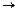 I
I
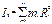 (2)
(2)
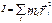 (3)
(3)
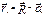 (4)
(4)
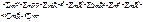
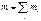 (6)
(6) 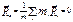 (5)
(5)
Ф-ла (2) и (5) 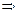
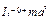
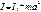 (7)
(7)
Формула (7) выражает теорему Гюйгенса-Штейнера.
№36. Движение тел с переменной массой.
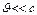 ,
,
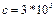 км/с
км/с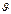
речь не идет о релятивистском изменении массы.
Мы называем тело телом с переменной массой если в процессе его движения масса тела меняется за счет потери или приобретения вещества.пример: 3-х ступенчатая ракета. Выгорает топливо, масса уменьшается.
Для получения уравнения движения тела с переменной массой нет необходимости привлечения новых физ. Принципов. Это ур-е следует из законов Ньютона.(см. и1 лекции 20 )
Пусть имеется ракета (см и1) которая имеет массу М(t).Пусть в неподвижной ИСО S скорость ракеты равна 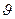 .Пусть в течении малого времени dt происходит выброс массы dm, причем скорость выброса есть u.Мы считаем что система замкнутая, для таких систем выполняется закон сохранения импульса, выполняется закон сохр. массы. Обозначим dM- уменьшение массы ракеты за dt.
.Пусть в течении малого времени dt происходит выброс массы dm, причем скорость выброса есть u.Мы считаем что система замкнутая, для таких систем выполняется закон сохранения импульса, выполняется закон сохр. массы. Обозначим dM- уменьшение массы ракеты за dt.
dM<0 (2) следовательно мы имеем: dM+dm=0 (3)- закон сохранения массы. Импульс системы в момент времени t: 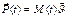 (4)
(4)
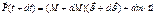 (5)
(5)
Для общего случая: 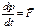 (6)
(6)
Когда действует внешняя сила: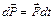 (7)
(7)
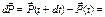

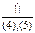 Получаем:
Получаем: 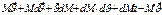
Мы пренебрегаем произведением 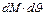 как величину 2-го порядка малости
как величину 2-го порядка малости
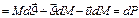 (8)
(8)
Мы учтем силу для общего случая: 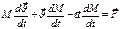
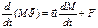 (9)
(9)
Уравнение (9) описывает движение тела с переменной массой в ИСО S при наличии внешних сил F.
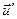 - относительная скорость газов относительно ракеты, тогда относительно S
- относительная скорость газов относительно ракеты, тогда относительно S
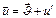 (10)
(10)
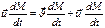 (11)
(11)
Расписываем левую часть (9):
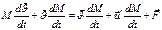
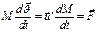 (12)
(12)
Обозначим через 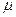 ежесекундный расход топлива
ежесекундный расход топлива
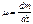 (13) {кг/с}
(13) {кг/с}
с учетом (3) перепишем (13)
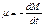 (14)
(14)
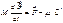 (15)
(15)
Формула (15) есть главная формула данного вопроса.
Вектор 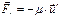 (16) назовем реактивной силой.
(16) назовем реактивной силой.
Уравнение (15) называется уравнением Мещерского или уравнением движения тела с переменной массой для общего случая(в присутствии F).
№37. Формула Циолковского.
(см. и2 в лекции 20)
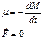 (1)
(1)
Спроецируем 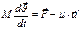 с учетом (1) на ось Z
с учетом (1) на ось Z

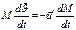
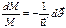 (2)
(2)
Обозначим 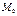 ,
,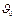 - значения массы и скорости перед включением двигателя ракеты
- значения массы и скорости перед включением двигателя ракеты
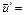 const
const
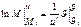
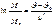 (3)
(3)
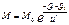 (4)
(4)
Формула (4) называется формулой Циолковского. Эта формула показывает насколько изменится масса ракеты при увеличении скорости от 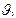 до
до 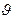 . Из этой формулы можно узнать насколько изменится скорость ракеты.
. Из этой формулы можно узнать насколько изменится скорость ракеты. 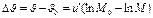 (5)
(5)
Из этой формулы видно, что для увеличения скорости при минимальном расходе топлива нужно увеличивать 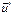 .
.
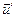 =(4~5)км/с
=(4~5)км/с
На практике используют ступенчатый принцип. Идею 3-х ступенчатой ракеты предложил Циолковский.
№38. Столкновения. Законы сохранения при столкновениях.
Пример: столкновение 2-х бильярдных шаров
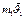
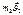
.Если шары столкнулись, скорости их изменились, при этом происходит удар. Более сложный- опыт Резерфорда в котором изучалось столкновение 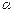 - частиц с ядрами вещества.(см. и3 лекции 20)
- частиц с ядрами вещества.(см. и3 лекции 20)
При этом скорость меняется от 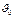 до
до 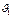 , и прямого удара не было.
, и прямого удара не было.
Таким образом, есть только изменение скорости, но в физике это тоже относится к столкновению.
Столкновением называется взаимодействие 2-х или более тел (частиц) которое происходит в относительно малой области пространства и в течении малого времени, при этом скорости тел до взаимодействия и после взаимодействия измеренные в точках 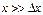 и времени
и времени 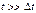 отличаются друг от друга.
отличаются друг от друга.
(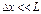 ) L ~ x
) L ~ x
(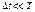 ) T ~ t
) T ~ t
L и T к А правило параметры установки.
При столкновениях, как правило происходит изменение импульса, момента импульса, и энергии частиц.
Выполняются законы сохранения:
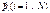 Мы учитываем рождение и уничтожение частиц.
Мы учитываем рождение и уничтожение частиц.
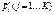
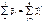 (1)
(1)
Ф - ла (1) выражает закон сохранения импульса при столкновении частиц.
Мы знаем, что при ударе часть кинетической энергии шара уходит в тепло за счет неупругих деформаций
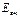 ,
, 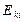 -до удара
-до удара
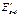 ,
, 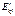 -после удара
-после удара
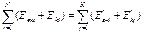 (2)
(2)
Ф – ла (2) выражает закон сохранения полной энергии при сохранении частиц.
№39. Абсолютно упругое столкновение двух шаров.
Если внутренняя энергия частиц после столкновения не изменяется, то такое столкновение называется упругим.
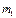 ,
, 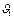
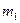 ,
,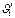
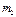 ,
,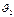
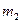 ,
,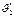
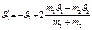
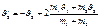
Если 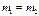 , то
, то 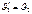 ,
, 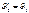 .
.
При столкновении двух одинаковых шаров, они обмениваются скоростями.
№40. Абсолютно неупругое столкновение двух шаров.
Если внутренняя энергия частиц после столкновения изменяется, то такое столкновение называется неупругим. Это столкновение двух тел, в результате которого они соединяются вместе и движутся дальше как одно тело.
Обозначим через V общую скорость шаров после столкновения. Закон сохранения импульса дает:
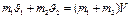 , где
, где 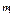 и
и 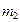 - массы шаров. Отсюда получим:
- массы шаров. Отсюда получим:
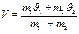
Кинетические энергии системы до удара и после удара равны соответственно:
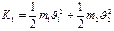 ,
, 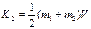
отсюда получим:
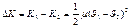 , где
, где 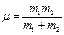 - приведенная масса шаров.
- приведенная масса шаров.
Таким образом, при столкновении двух абсолютно неупругих шаров происходит потеря кинетической энергии макроскопического движения, равная половине произведения приведенной массы на квадрат относительной скорости.
43.Математический маятник
(см. Л.№17.И.6)
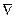 Система (И.6) и состоящая из нерастяжимой нити длиной
Система (И.6) и состоящая из нерастяжимой нити длиной 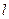 ,подвешенная в точке О. С сосредоточенной массой
,подвешенная в точке О. С сосредоточенной массой 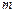 и находящаяся в поле силы тяжести называется математическим маятником .Мы считаем эту массу материальной точкой.
и находящаяся в поле силы тяжести называется математическим маятником .Мы считаем эту массу материальной точкой.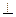
Найти закон движения м.т. на И.6 если ей сообщена либо начальная скорость, либо угол отклонения ,либо начальный импульс.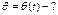
В основе решения любой задачи лежит закон природы. В данном случае это второй закон Ньютона записанный для вращательного движения 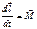 (1)
(1)
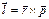 ;
; 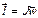 (2)
(2) 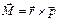 (3) Сила натяжения нити не создает момента т.к.
(3) Сила натяжения нити не создает момента т.к.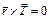 .
.
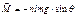 (4) Проецируем ур-е (1)
(4) Проецируем ур-е (1) 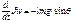 (5) ;
(5) ; 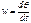 (6)
(6)
Подставляя (6) в (5) получаем: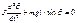 (7)
(7)
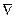 Ур-е (7) называется дифференц. Ур-ем движения математического маятника
Ур-е (7) называется дифференц. Ур-ем движения математического маятника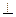 Это не линейное ур-е.
Это не линейное ур-е.
Для решения (7) мы рассмотрим случай малых колебаний, именно он и реализуется в часах. 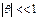 (8).
(8).
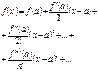 (9)
(9)
 Ф.(9) называется рядом Тейлора
Ф.(9) называется рядом Тейлора
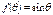 ;
; 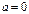 ;
; 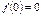 ;
; 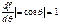
При выполнении (8) ряд Тейлора можно оборвать на первом не нулевом члене. 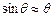 (10) С учетом (10) получаем
(10) С учетом (10) получаем 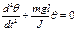 (11)
(11)
 Ур-е (11) называется линейным диф. Ур-ем движения математического маятника
Ур-е (11) называется линейным диф. Ур-ем движения математического маятника
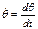 ;
; 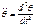 (12);
(12); 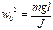 (13);
(13); 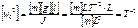
Мы показали, что этот параметр введенный по формуле (13) имеет размерность квадрат частоты. С учетом (12) и (13) и (11) приобретает следующий вид: 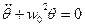 (14)
(14)
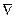 Это линейное дифференциальное ур-е движения математического маятника
Это линейное дифференциальное ур-е движения математического маятника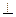
ОЗМ: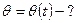
Ур-е (14) решается стандартными методами ОДУ.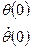 -задано (15)
-задано (15)
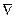 В теории ОДУ ур-е (14) совместно с (15) которое записывается в след. Виде:
В теории ОДУ ур-е (14) совместно с (15) которое записывается в след. Виде: 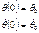 -(16) называется задачей Коши и имеет единственное решение.
-(16) называется задачей Коши и имеет единственное решение.
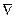 Решением ур-я называется такая ф-ия
Решением ур-я называется такая ф-ия 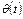 , которая будучи подставлена в ур-е (14)представляет его в верное тождество
, которая будучи подставлена в ур-е (14)представляет его в верное тождество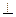
Мы покажем , что 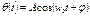 (17);
(17); 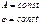 -(18) является решением.
-(18) является решением.
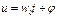 ;
; 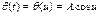 ;
;
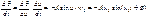 ;
;
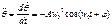 (19) Подставляем (19) и (17) в левую часть ур-я (14).
(19) Подставляем (19) и (17) в левую часть ур-я (14).
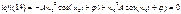
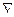 Мы видим, что искомое решение ур-я (14) представляет собой гармоническую ф-ию времени и периодическую.
Мы видим, что искомое решение ур-я (14) представляет собой гармоническую ф-ию времени и периодическую.
 По этой причине говорят, что система изобр.на (И.6) совершает колебания, т.е.периодические движения вокруг одной точки, которая является положением равновесия.
По этой причине говорят, что система изобр.на (И.6) совершает колебания, т.е.периодические движения вокруг одной точки, которая является положением равновесия.
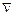 Величина А в законе движения (17) называется амплитудой колебаний
Величина А в законе движения (17) называется амплитудой колебаний 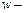 круговая частота,
круговая частота, 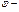 начальная фаза.
начальная фаза.
Мы показали, что 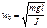 (20); из и.6 видно, что
(20); из и.6 видно, что 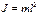 (21); (21) в (20), получим
(21); (21) в (20), получим 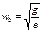 (22);
(22); 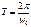 (23);
(23); 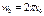 (24);
(24);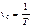 ;
; 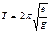 (25);
(25);
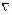 Ф.(25) дает период колебаний математического маятника. Мы вывели ее исходя из ур-я (14) и решения (17). Отметим, что Т независит от массы, а определяется только длиной нити и ускорением
Ф.(25) дает период колебаний математического маятника. Мы вывели ее исходя из ур-я (14) и решения (17). Отметим, что Т независит от массы, а определяется только длиной нити и ускорением 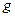 .
.