Для электростатического поля в вакууме
Вычисление напряженностей простейших электростатических полей, генерируемых точечными зарядами решается в рамках закона Кулона. Однако вычисление напряженности электростатического поля, генерируемого телом конечных геометрических размеров в рамках применимости закона Кулона, задача трудоемкая. Решение этой задачи для электростатического поля в вакууме дает теорема Гаусса-Остроградского, которая формулируется следующим образом: поток вектора напряженности электростатического поля в вакууме через любую произвольно замкнутую поверхность равен сумме зарядов, заключенных внутри этой поверхности, отнесенной к диэлектрической проницаемости вакуума. Математически теорема Гаусса-Остроградского записывается следующим образом:
 . .
| (18) |
Применим теорему Гаусса-Остроградского к вычислению напряженностей электрического поля, генерируемых простейшими телами.
1.6.1. Электростатическое поле заряженной сферы
Сфера, представляет собой тонкую оболочку радиуса R, натянутую на шар. Внутри сферы и за ней вакуум. Пусть сфера заряжена до заряда Q. Гауссову поверхность удобно взять в виде сферы радиуса r, концентричной заряженной сфере, изображенных на рис.3, поскольку система зарядов на сфере центральносимметрична.
Внутри сферы, при r<R, зарядов нет, поэтому теорема Гаусса для этого случая запишется:
 . .
|
За сферой, при R>r, находится единственный заряд сферы Q и в силу центральносимметричности электростатического поля:
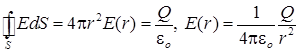 при r>R. при r>R.
|
Видно, что формула напряженности электрического поля за сферой подобна формуле (7) напряженности поля точечного заряда.


 r
r
 |
 Q
Q
r
Рис.3. Пояснение к вычислению напряженности электрического поля, заряженной сферы
Получили, что внутри заряженной сферы электрическое поле отсутствует. Этот факт, можно использовать для защиты (экранировки) от электрических полей. Применяя связь между потенциалом и напряженностью электрического поля (13), вычислим потенциал поля сферы:

|
1.6.2. Электростатическое поле заряженного шара
Пусть шар, радиуса R несет на себе равномерно распределенный по объему заряд Q. Тогда, аналогично, как и для сферы, запишем теорему Гаусса-Остроградского внутри и за шаром. Внутри шара:
 . .
|
После приравнивания левой и правой частей теоремы Гаусса имеем:
 . .
|
За шаром, напряженность электрического поля эквивалентна напряженности за сферой и вычисляется точно также, как и для сферы:
 при r>R. при r>R.
|
В силу (13), потенциал поля заряженного шара, будет равен:
 . .
|
1.6.3. Электростатическое поле заряженной бесконечной плоскости
Теорему Гаусса-Остроградского можно применять, к расчету полей гладких поверхностей. Если поверхность имеет острые выступы, то в силу определения направления вектора напряженности электрического поля, напряженность поля идеального острия равна бесконечности. Поэтому для расчета полей, генерируемых не гладкими поверхностями (плоскость, цилиндр и т.д.) необходимо исключить влияние неопределенности на острых выступах. Поэтому можно точно говорить о напряженности поля заряженной до заряда Q бесконечной плоскости на расстоянии r по нормали к ней.
Гауссова поверхность в данном случае проводится как параллелепипед, в плоскости симметрии которого находится заряженная плоскость. Тогда теорема Гаусса-Остроградского для плоскости:
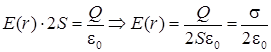 , ,
|
где S – площадь плоскости, s – поверхностная плотность зарядов.
Потенциал поля плоскости в силу (13) равен:
 . .
|
1.6.4. Электростатическое поле заряженного бесконечно длинного цилиндра
и тонкой заряженной нити
Применяя теорему Гаусса-Остроградского можно вычислить напряженность электростатического поля, генерируемого бесконечно длинным цилиндром, заряженным до заряда Q на расстоянии r от его оси. Под понятием бесконечно длинного цилиндра, здесь подразумевается цилиндр, радиус основания которого R много меньше длины образующей l. Частным случаем такого цилиндра будет тонкая нить или длинный провод.
Если заряд по цилиндру распределен равномерно, то за гауссову поверхность в виду осевой симметрии зарядов можно взять коаксиальный цилиндр, радиуса r. Поскольку R<<l, то поток вектора напряженности, через основания считаем много меньше чем через боковую поверхность. Это допущение сделано и для того, чтобы исключить скачок напряженности на границе боковая сторона – основание.
Тогда, теорема Гаусса-Остроградского, за цилиндром:
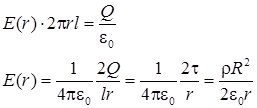 при r>R. при r>R.
|
Для поля внутри цилиндра имеем:
 при r<R. при r<R.
|
Потенциал поля цилиндра на расстоянии r от его оси:
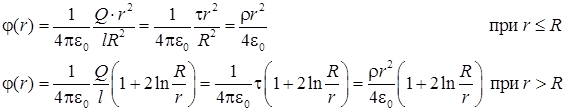 . .
|