Трудоемкость изучения дисциплины Физика по специальностям ОмГАУ нужна таблица!!! Специальности

ВВЕДЕНИЕ

 

Данные методические указания разработаны по циклу МЕН по разделу «Механика» дисциплины «Физика» в соответствии с рабочими программами, предназначенными для всех специальностей и направлений подготовки бакалавров факультетов технического сервиса в АПК, водохозяйственного строительства, технологии молочных продуктов, агрономического и землеустроительного факультетов, а также факультета агрохимии, почвоведения и экологии.

Цель данных методических указаний – помочь студентам выполнить лабораторные работы, научить правильно определять погрешности и производить необходимую математическую обработку результатов эксперимента.

Методические указания даны к выполнению лабораторных работ по следующим темам:

1. Измерение параметров тел (1, 2).

2. Поступательное движение тел (6).

3. Вращательное движение тел (7).

4. Колебательное движение тел (3, 4, 5, 8, 9).

Трудоемкость каждой лабораторной равна двум часам аудиторной и двум часам внеаудиторной работы.

Трудоемкость изучения всей дисциплины «Физика» зависит от того, студентам какого факультета и какой специальности она предназначена.

 

Трудоемкость изучения дисциплины «Физика» по специальностям ОмГАУ (нужна таблица!!! )

 

Специальности	Трудоемкость изучения, ч
дисциплины	В том числе раздела «Механика»
Всего	Из них лаб. занятий
260400, 310200, 310300, 310600
310100, 320400
311300, 311400, 311900
311100, 310900, 311000

 

Данные методические указания издаются в комплексе с заданиями к самостоятельной работе студентов по физике.

ОБЩИЕ РЕКОМЕНДАЦИИ

 

Процесс выполнения лабораторных работ включает теоретическую подготовку, знакомство с приборами и материалами, проведение опыта и измерений, числовую обработку результатов лабораторного эксперимента и написание отчета по выполненной работе.

Теоретически подготовиться к выполнению эксперимента студент должен самостоятельно. Необходимо внимательно проработать указания к данной лабораторной работе, а для более глубокого изучения рассматриваемого явления следует обратиться к литературным источникам, перечень которых помещен в конце указаний.

Опыты и измерения выполняют в аудитории после краткого собеседования с преподавателем по контрольным вопросам, которые приводятся в конце каждой лабораторной работы.

Теоретическая подготовка завершается составлением отчета в тетради для лабораторных работ по следующему плану:

а) название работы;

б) цель ее;

в) явления, положенные в основу этой работы;

г) терминология: модели, физические понятия, физические величины (определения, определяющие уравнения); принципы и законы, формулы связи;

д) принципиальная и рабочая схемы установки;

е) расчетная формула;

ж) таблицы измеряемых и расчетных величин;

з) оценка результатов измерений (сравнить с табличными значениями, объяснить вид графика);

и) источник ошибок и погрешностей (при выполнении лабораторной работы, при изготовлении установки).

КЛАССИФИКАЦИЯ ОШИБОК ИЗМЕРЕНИЯ

 

Любая физическая величина может быть измерена путем сравнения её с однородной величиной, принятой за единицу (эталоном).

Измерения бывают прямые и косвенные. В результате прямых измерений определяемая физическая величина получается сразу, непосредственно. Примерами прямых измерений служат определения длины (линейкой, штангенциркулем), силы электрического тока (амперметром). При косвенных измерениях искомая величина вычисляется по результатам прямых измерений других величин, связанных с искомой некоторой формулой.

Любое измерение не может быть абсолютно точным. Между истинным Х_ИСТ и измеренным значением физической величины Х существует некоторая разность

ΔХ = ЅХ – Х_ИСТЅ, (1.1)

которая называется абсолютной ошибкой результата измерения.

Чтобы охарактеризовать качество измерения и иметь возможность сравнить результаты измерений различных физических величин, вводится понятие относительной погрешности, под которым подразумевают отношение абсолютной ошибки измерения к истинному значению измеряемой величины.

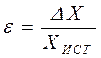. (1.2)

Чем меньше относительная погрешность, тем выше точность измерения. Погрешности, или ошибки измерения, можно разделить на три класса: грубые ошибки, или промахи; систематические ошибки; случайные ошибки.

Грубые ошибки появляются в результате небрежности, невнимательности экспериментатора (неправильные отсчеты по прибору, неправильная запись результата и т.п.). В большинстве случаев промахи хорошо заметны, так как резко отличаются от результатов других измерений.

Систематические ошибки могут быть вызваны методикой постановки эксперимента, ограниченной точностью измерительных приборов, дефектами самого объекта исследования и т.д. Величина и знак систематической погрешности могут оставаться неизменными при многократном повторении одних и тех же измерений. В некоторых случаях влияние систематических погрешностей на результат измерения можно учесть, если ввести соответствующие поправки.

Случайные ошибки обусловлены действием самых разнообразных и неконтролируемых причин. Поэтому результаты повторных измерений одной и той же физической величины могут не совпадать даже при том, что они проводятся в неизменных условиях одним и тем же методом (такие измерения называют равноточными).

Случайные ошибки могут иметь любую величину, положительный или отрицательный знак. Ошибки, противоположные по знаку, но равные по абсолютной величине, встречаются в среднем одинаково часто. Закономерности, которым подчиняются случайные ошибки, и способы их оценки изучают в разделе математики «Теория ошибок», основанном на законах теории вероятности и математической статистики.

 

Методика расчета случайных ошибок прямых измерений

Пусть измеряется n раз некоторая физическая величина Х. Из-за случайных погрешностей, возникающих в процессе измерения, мы получаем набор значений… . (1.3) Чем больше измерений, тем ближе < X > и ХИСТ, а при

Коэффициент Стьюдента

  Таким образом, порядок расчета случайной ошибки измерения должен быть… а) производят n измерений искомой физической величины и вычисляют ее среднее значение

Систематические ошибки. Соотношение случайной и систематической ошибок

Систематические ошибки могут существенно исказить результат измерения, поэтому перед началом измерений необходимо выявить систематические ошибки и,… Таким образом, в результате обработки данных, полученных при измерении, мы… К какому же отношению между величинами случайной и систематической погрешностей следует стремиться при проведении…

Методика расчета погрешностей косвенных измерений

, искомое значение ХХХ находят путем подстановки в формулу (1.3) средних… Искомую функцию (расчетную формулу) логарифмируют:

Теория линейного нониуса

Линейный нониус представляет собой небольшую линейку N, скользящую вдоль обычной линейки. Пусть на нониусе m делений (рис. 1.1), которые наносят так, чтобы длина всех… или

Задание 1. Предварительная оценка точности измерения

 

1. Определить линейные размеры тел с помощью различных измерительных приборов: линейки, штангенциркуля, микрометра.

2. Рассчитать относительные ошибки каждого прямого измерения. В качестве абсолютных погрешностей результатов прямых измерений следует взять приборные ошибки.

3. Сравнить относительные погрешности всех прямых измерений и выделить наименее точно измеренную величину. Для ее определения следует выбрать из имеющегося набора измерительных приборов наиболее точный. Приборы для определения остальных величин подбирают так, чтобы их относительная ошибка была на порядок меньше относительной ошибки наименее точно измеренной величины или того же порядка. Результаты предварительной оценки точности измерения представить в виде табл. 1.2 и сделать заключение.

Таблица 1.2

Предварительная оценка точности измерения

 

Задание 2. Определение линейных размеров тел правильной геометрической формы

 

1. Штангенциркулем не менее пяти раз измерить диаметр цилиндра.

2. Микрометром не менее пяти раз измерить диаметр цилиндра.

3. Рассчитать доверительный интервал и относительную погрешность измерений диаметра цилиндра с помощью штангенциркуля и микрометра при доверительной вероятности a = 0,95. Данные занести в табл. 1.3.

Таблица 1.3

Измеряемые величины для определения размеров тела правильной геометрической формы

  Окончательный результат записать в виде hшт. = < h > ± ∆h, d = < d > ± ∆d, при a = 0,95.

Контрольные вопросы

 

1. Выведите формулу для расчета точности нониуса.

2. Каким прибором следует воспользоваться, если один и тот же линейный размер тела можно измерить штангенциркулем и микрометром?

3. Как рассчитать доверительный интервал непосредственно измеряемой величины?

4. Из каких соображений выбирают число измерений? Как зависят точность результата отдельных измерений и точность среднего результата от числа измерений?

5. Каков смысл записи h = < h> ± ∆h, при α = 0,95?

6. Объясните, с чем связан разброс результатов отдельных измерений линейных размеров.

 

Литература [3, § 62, 66, 68, 75; 1, § 27, 30, 31].

 

Лабораторная работа 2. ИЗМЕРЕНИЕ ВРЕМЕНИ И МАССЫ (4 ч)

 

Цель – освоить метод отсчёта отрезков времени и метод измерения массы, основанный на инертных свойствах тела.

Приборы и материалы: электрический секундомер, пружинный маятник с набором грузов.

 

Основные единицы системы СИ и их реализация

Международная система единиц измерения физических величин (СИ) была установлена в международных масштабах в 1960 г. и введена в нашей стране в… В качестве единицы длины (метр) была первоначально принята величина, равная… Успехи в развитии оптики и атомной физики позволили сопоставить метр с длиной светового излучения, создать новый…

Описание установки и методов измерений

Колебания пружинного маятника при малых амплитудах происходят по гармоническому закону , где х – смещение точки от положения равновесия в данный момент времени; А – амплитуда смещения; – фаза калебания,…

Задание 1. Измерение отрезков времени

 

1. Подключить секундомер к электрической сети.

2. Включив секундомер, начать вслух, не торопясь считать: двадцать один, двадцать два и т.д. Закончив счёт на тридцати, выключить секундомер.

3. Определить время произношения одного двузначного числа. Повторить опыт три раза и найти среднее значение этой величины.

4. Нащупать свой пульс и, включив секундомер, подсчитать число ударов пульса за 30 с (учитывайте число оборотов маленькой стрелки секундомера). Измерить пульс у каждого экспериментатора.

 

Задание 2. Измерение массы с помощью пружинного маятника

 

1. Для определения жёсткости пружины измерить период колебаний маятника с известной массой m₀. Массу m₀ подобрать так, чтобы период не был очень мал (полная масса m₀ включает в себя массу стержня и дисков, надеваемых на него). Вывести маятник из положения равновесия на 2–3 см. Для повышения точности измерить время 10–20 периодов.

2. Надеть на стержень тело неизвестной (большей) массы и аналогичным образом определить период Т_Х. По формуле (2.3) определить полную массу. Вычтя из полной массы массу стержня, найти массу этого тела. Все данные занести в табл. 2.1.

 

Таблица 2.1

Измеряемые и расчетные величины для определения массы

 

Контрольные вопросы

 

1. Выразите в километрах длину земного меридиана.

2. Выразите в килограммах массу 1 дм³ воды.

3. Что является эталоном длины, массы, времени?

4. Какой закон природы определяет соотношение между силой и ускорением тела?

5. Перечислите наиболее распространённые методы измерения массы. Какие методы пригодны для измерения массы в условиях невесомости?

6. В чём различие понятий инертной и гравитационной масс? Равны ли они по величине?

7. Какая масса (инертная или гравитационная) измеряется в данной работе?

8. Какая масса (инертная или гравитационная) измеряется с помощью пружинного динамометра?

9. Какие периодические процессы используются для измерения времени?

10. Зависит ли период колебаний пружинного маятника от ускорения свободного падения?

 

Литература [3, т. 1].

Лабораторная работа 3. ОПРЕДЕЛЕНИЕ МАССЫ ТЕЛА
С ПОМОЩЬЮ ПРУЖИННОГО МАЯТНИКА (4 ч)

Цель – ознакомиться с одним из способов экспериментального определения массы тела с помощью пружинного маятника.

Этот способ используется при определении массы тела массметром – прибором, который, например, применяется в экспериментах по взвешиванию космонавтов на орбитальных станциях.

Приборы и материалы: пружина, кронштейн, площадка с набором грузов, секундомер, пластинка.

 

Описание установки и метода измерения

Установка состоит из пружины, верхний конец которой жёстко соединён с кронштейном. К нижнему концу пружины подвешивается площадка, на которую можно… Гармонические колебания тела массой m1, подвешенного на пружине жёсткостью k1,… . (3.1)

Задание 1. Определение массы тела, когда измеряемая масса представляет собой величину одного порядка с эталонной массой

 

1. Подвесить к пружине грузик с известной массой m_э и определить время t_э, за которое маятник совершает N колебаний (N = 30–50).

2. Подвесить к пружине грузик с неизвестной массой m и определить время t, за которое маятник совершает столько же колебаний N (N = 30–50).

3. Повторить опыт (пп. 1, 2) пять раз, результаты измерений занести в табл. 3.1.

4. Рассчитать по формуле (3.4) массу неизвестного тела.

 

Таблица 3.1

Измеряемые и расчетные величины для определения массы тела
с помощью пружинного маятника (m ≈ m_э)

 

№

 

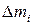
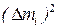
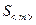
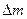
Задание 2. Определение массы тела, если существует большое различие между измеряемой и эталонной массами

 

1. Подвесить к пружине грузик с эталонной массой и прикрепить к грузику пластинку (m = m_э), определить время t, за которое маятник совершает число колебаний, равное числу колебаний, определённых в п. 1 задания 1.

2. Взяв данные t_э из п. 1 задания 1 и t, (m + m_э) из п. 1 задания 2, определить неизвестную массу по формуле (3.5).

3. Опыт повторить пять раз, результаты измерений занести в табл. 3.2.

4. Определить погрешность измерений массы и записать конечный результат в виде при .

5. Сравнить результаты эксперимента с данными, полученными взвешиванием исследуемых тел на рычажных весах .

Таблица 3.2

Измеряемые и расчетные величины для определения массы тела
с помощью пружинного маятника (m >> m_э)

 

№

 

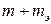
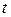
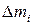
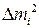
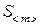
Контрольные вопросы

1. Какое колебание называется гармоническим?

2. Что называется амплитудой, периодом, частотой, фазой колебаний?

3. Выведите формулу периода колебаний пружинного маятника.

4. Получите рабочие формулы (3.4) и (3.5).

5. Что понимают под массой тела?

6. Какими способами можно определить массу тела?

7. В чём состоит сущность основного закона взаимодействия?

 

Литература [5, § 141, 142].

Лабораторная работа 4. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА
УПРУГОСТИ ПРУЖИНЫ (4 ч)

 

Цель – определить коэффициент упругости пружины двумя способами: 1) используя зависимость периода упругих колебаний от массы; 2) по закону Гука.

Приборы и материалы: пружина, площадка для грузов, набор грузов, секундомер, линейка.

Описание установки

 

Установка (рис. 4.1, 4.2) представляет собой пружину, верхний конец которой жестко соединен с кронштейном. К кронштейну прикреплена измерительная линейка. К нижнему концу пружины подвешивается площадка, на которую можно помещать различный набор грузов.

 

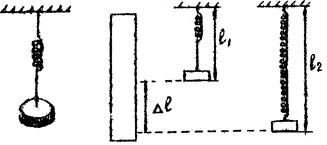
Рис. 4.1 Рис. 4.2

Задание 1. Определение коэффициента упругости пружины по закону Гука

 

1. Записать формулу для определения коэффициента упругости по закону Гука.

2. Продумать и записать порядок выполнения работы (рис. 4.2).

3. Составить таблицу для значений измеряемых величин и произвести необходимые измерения.

 

Задание 2. Определение коэффициента упругости пружины из зависимости периода упругих колебаний от массы груза

 

1. Навесить на пружину груз в 100 г, при этом общая масса будет равна

, (4.1)

где m_np – масса пружины,

m_гр – масса груза,

т_пл – масса площадки.

2. Слегка оттянуть пружину и отпустить. Система придет в колебательное движение. По секундомеру определить время t, в течение которого происходит 20–30 полных колебаний системы. Опыт повторить не менее трех раз и найти среднее значение < t >. Из полученных данных определить средний период < T > по формуле

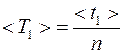. (4.2)

3. Добавляя грузы по 100 г, аналогично определить < T₂ >,< T₃ >.

4. Полученные данные занести в табл. 4.1.

5. Для каждого значения периода < T > определить коэффициент упругости пружины K₁ , K₂ , K₃ из формулы

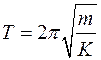, откуда .

Найти среднее значение < K >.

6. Сравнить значения коэффициента упругости, полученные при выполнении заданий 1 и 2.

7. Сделать выводы.

 

Таблица 4.1

Измеряемые и расчетные величины для определения коэффициента упругости К

 

Контрольные вопросы

 

1. Дайте определение гармонического колебания.

2. Дайте определение кинематических характеристик гармонического колебания: амплитуды, периода, частоты, фазы колебания.

3. Запишите уравнения смещения, скорости и ускорения при колебательном движении, их максимальные значения.

4. Получите формулу периода упругих колебаний.

5. Объясните физический смысл коэффициента упругости.

 

Литература [5, § 141, 142].

 

Лабораторная работа 5. ОПРЕДЕЛЕНИЕ СИЛЫ ЗЕМНОГО
ПРИТЯЖЕНИЯ С ПОМОЩЬЮ МАТЕМАТИЧЕСКОГО МАЯТНИКА (4 ч)

 

Цель – экспериментально определить модуль ускорения силы земного тяготения в данном географическом месте.

Приборы и материалы: маятник на нити изменяемой длины, шкалы с подвижным угольником и двумя барабанами, секундомер.

Описание установки

Установка представляет собой тело 1, подвешенное на двух нерастяжимых нитях 2. Нить перекинута через барабан 3 и кронштейн 4. Два барабана и… Рис 5.1 Рис 5.2 Рис 5.3

Задание. Определение ускорения силы земного тяготения

 

1. Отметить подвижным угольником положение нижнего края маятника по шкале.

2. Отклонить маятник на угол 5–6° (на ширину линейки 5).

3. Определить с помощью секундомера время 50 полных колебаний, начиная отсчет в момент наибольшего отклонения маятника от положения равновесия. Время N колебаний для неизменной длины l₁ измерить трижды.

4. Поднять шарик на 40–50 см, наматывая нить на барабан. При новой длине l₂ время N полных колебаний измерить так же три раза.

5. Определить периоды T₁ и T₂ по формуле .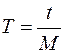

6. По формуле (5.3) рассчитать ускорение силы земного тяготения, используя среднее значение периодов.

7. Измеренные параметры и полученные в результате вычислений данные занести в табл. 5.1

Таблица 5.1

Измеряемые и расчетные величины для определения ускорения свободного падения

Контрольные вопросы

 

1. Какое колебательное движение называется гармоническим?

2. Дайте определение амплитуды, периода, фазы колебаний.

3. Выведите уравнения скорости и ускорения при гармоническом колебательном движении.

4. Изобразите графически зависимость от времени амплитуды, периода, смещения, скорости и ускорения при гармоническом колебательном движении.

5. Дайте определение математического маятника, периода его колебаний.

6. Чему равна энергия гармонических колебаний? Выведите формулу периода колебаний. Сформулируйте закон сохранения энергии при гармонических колебаниях.

7. В чем отличие собственных и вынужденных колебаний?

 

Литература [3, § 62, 66, 68, 75; 4, § 27, 30, 31].

 

Лабораторная работа 6. ИЗУЧЕНИЕ ЗАКОНОВ СОХРАНЕНИЯ
ИМПУЛЬСА И ЭНЕРГИИ ПРИ УПРУГОМ УДАРЕ (4 ч)

 

Цель – ознакомиться с явлением удара на примере соударения подвешенных на нитях упругих шаров.

Приборы и материалы: измерительная установка, набор шаров.

 

Рис. 6.1

 

Измерительная установка (рис. 6.1) представляет собой основание 1 на трех регулируемых винтах 9 для выверки ее по уровню. На основании смонтирована стойка 4, несущая подвески 5 шаров 3 и штангу 6, на которой крепится электромагнит 7. Для отсчета положения шаров имеются две шкалы, проградуированные в градусной мере. Первая шкала 8 установлена так, что указатель положения правого шара в положении равновесия располагается над нулевой отметкой шкалы. Левая шкала 2 может перемещаться, ее следует расположить так, чтобы нулевая отметка находилась против указателя левого шара в положении равновесия последнего. Электромагнит 7, служащий для удержания правого шара в исходном положении для бросания, закрепляется в нулевом положении винтом, находящимся на оправке электромагнита. Питание электромагнита осуществляется постоянным током напряжением 6 В. Все шары имеют указатель равновесия и крючок для подвеса, а шары из немагнитных материалов – специальные металлические накладки для удержания их электромагнитом.

В данной работе рассматривается удар шаров, подвешенных в виде маятника, причем один шар до удара покоится (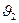= 0).

Удар происходит в положении, соответствующем равновесию тел, и является центральным, прямым и упругим.

 

Задание 1. Определение коэффициента восстановления энергии при упругом ударе

 

1. Проверить горизонтальность основания установки. При необходимости откорректировать ее с помощью винтов 9.

2. Подвесить упругие шары и произвести центровку.

3. Отвести правый шар в крайнее положение на до соприкосновения с электромагнитом.

4. Разомкнув цепь электромагнита, произвести удар правым шаром по находящемуся в равновесии левому шару, взять отсчет первого отброса обоих шаров α₁ и α₂. Удар из данного положения повторить не менее пяти раз. Результаты измерения занести в табл. 6.1.

5. Используя закон сохранения механической энергии, получим значения скоростей шаров до и после удара:

,

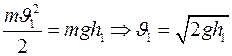соответственно

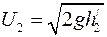, , (6.1)

где J₁ – скорость первого шара до удара;

U₁, U₂ – скорость шаров после удара;

– высота, с которой падает правый шар;

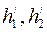– высота поднятия шаров после удара.

 

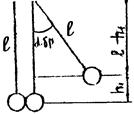
Рис. 6.2

 

Для определения высоты поднятия шара воспользуемся рис. 6.2, из которого видно, что 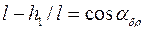, откуда 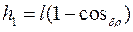или .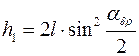

6. Подставив значения h₁ в формулы (6.1), получим соответственно

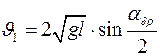, (6.2)

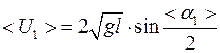, (6.3)

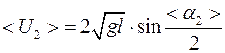, (6.4)

где 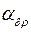– угол бросания первого шара;

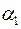<>, – средние значения углов отскока шаров.

7. Рассчитать средний коэффициент восстановления энергии 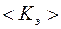(табл. 6.1), который характеризует рассеяние энергии по формуле

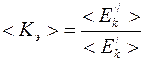, (6.5)

где – суммарная кинетическая энергия шаров до удара;

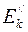– суммарная кинетическая энергия шаров после удара.

Используя формулы для расчета скоростей (6.2, 6.3, 6.4) и формулу расчета кинетической энергии, получим

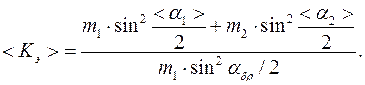(6.6)

Опыт провести для случаев: 1) ; 2) .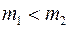

Оценить результат и сделать вывод.

 

Таблица 6.1

Измеряемые и расчетные величины для определения коэффициента восстановления энергии

 

Задание 2. Проверка закона сохранения импульса для упругого удара

 

1. Проверка закона сохранения импульса состоит в том, чтобы рассчитать значения скоростей U_1т и U_2т по теоретическим формулам, полученным из закона сохранения импульса и закона сохранения энергии, учитывая, что второй шар покоился:

(6.7)

Данные расчета занести в таблицу 6.2.

Таблица 6.2

Расчет теоретических значений скоростей после удара

; . Сделайте выводы.

Контрольные вопросы

 

1. Какой удар называется упругим?

2. Сформулируйте закон сохранения импульса для упругого удара, закон сохранения энергии для упругого удара.

3. Что называется коэффициентом восстановления энергии?

4. Каким должен быть коэффициент восстановления энергии в случае упругого удара?

5. Запишите формулы для расчета скоростей тел при упругом центральном ударе, дайте их анализ для случаев:

1) 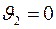, ; 2) ; .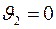

 

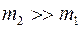Литература [3, § 28; 173].

 

 

Лабораторная работа 7. ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ
ТЕЛА (4 ч)

 

Цель – определить момент инерции тела неправильной формы (крестообразного маятника).

 

Приборы и материалы: исследуемое тело (крестообразный маятник), груз, приводящий маятник в движение (300–700 г), нить, на которой подвешен груз, вертикальная шкала, секундомер, прямоугольный треугольник, штангенциркуль.

 

Описание установки и метода измерения

Крестообразный маятник представляет собой металлическую ступицу А, вращающуюся с помощью подшипника относительно вала Б, который расположен… . (7.1)

Измеряемые и расчетные величины для определения момента инерции тела неправильной формы

Задание 2. Расчет относительных и абсолютных погрешностей

 

Так как косвенные измерения в данной работе производятся в невоспроизводимых условиях, то значение искомой величины вычисляют для каждого отдельного измерения, погрешность же рассчитывают так же, как и в случае прямых измерений.

Результаты расчета ошибок занести в табл. 7.2.

Таблица 7.2

Расчет ошибок

Окончательный результат записывают в виде при a = 0,95.  

Контрольные вопросы

 

1. Что называется абсолютно твердым телом? Дайте определение вращательного движения.

2. Что называется угловой скоростью, угловым ускорением? Какова связь между линейными и угловыми кинематическими величинами?

3. Что называется моментом инерции материальной точки, моментом инерции тела? Физический смысл момента инерции.

4. Как зависит момент инерции тела от положения оси вращения?

5. Сколько значений момента инерции может иметь данное тело?

6. Что называется моментом силы, плечом силы относительно оси вращения?

7. Какую роль играет маховое колесо, насаженное на вале двигателя трактора?

8. Проанализируйте возможные источники ошибок эксперимента.

9. Оцените погрешности однократных измерений диаметра шкива, высоты падения h, массы падающего груза m.

 

Литература [1, ч. 1, § 4, 5, 6, 21, 22, 23].

Лабораторная работа 8. ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ
МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ (4 ч)

 

Цель – определить момент инерции тела методом крутильных колебаний.

Приборы и материалы: измерительная установка, набор тел, секундомер.

 

Описание установки и метода измерения

Измерительная установка представляет собой круглый диск, подвешенный на упругой стальной проволоке и предназначенный для помещения тел, момент…  

Измеряемые и расчетные величины для определения момента инерции методом крутильных колебаний

 

Задание 1. Определение периодов крутильных колебаний прибора, прибора с эталоном, прибора с телом

 

1. Замерить секундомером время t_пр 20–30 полных колебаний прибора и определить .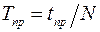

2. Опыт повторить 5 раз и определить < T_пр >.

3. Поместить на диск прибора эталон и аналогично определить < T₁ >.

4. Поместить на диск прибора тело, установку отцентрировать, определить < T₂ >.

Результаты измерений занести в табл. 8.1

 

Задание 2. Определение момента инерции тела

 

1. По полученным данным определить < f > и < J_пр >.

2. Рассчитать момент инерции тела относительно оси прибора, пользуясь формулой (8.3).

 

Контрольные вопросы

 

1. Какие колебания являются гармоническими крутильными?

2. Какой физический смысл имеют величины, входящие в основное уравнение динамики вращательного движения?

3. Чему равен период крутильных колебаний?

4. Какова идея метода определения моментов инерции тел с помощью крутильных колебаний?

5. От чего зависит момент инерции тела?

6. Как теоретически рассчитать момент инерции тела?

7. В чем физический смысл теоремы Штейнера?

8. Какова практическая необходимость определения моментов инерции тел?

9. Решите систему уравнений (8.1) и (8.2), выразив в явном виде J и f.

10. Выразите из уравнения (8.3) момент инерции тела J_т.

 

Литература [3, § 36, 39, 53].

Лабораторная работа 9. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ
ЗАТУХАЮЩИХ КОЛЕБАНИЙ ФИЗИЧЕСКОГО МАЯТНИКА (4 ч)

 

Цель – определить следующие параметры затухания физического маятника: период, частоту, логарифмический декремент затухания, добротность, коэффициент затухания и время релаксации колебательной системы.

Приборы и материалы: физический маятник в виде плоского диска со стрелочным указателем, шкала для отсчета смещения, секундомер.

 

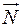При отклонении физического маятника на небольшой угол a от положения равновесия на него будут действовать три силы: сила тяжести , сила реакции опоры и сила сопротивления воздуха. Момент силы реакции опоры 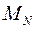будет равен нулю. Момент силы тяжести 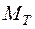можно рассчитать по формуле

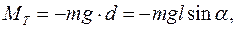(9.1)

где d – плечо силы тяжести;

l – расстояние ОС между точкой повеса О и центром маятника С.

При малых отклонениях маятника 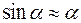. Знак «–» обусловлен тем, что вращательный момент M_T стремится вернуть маятник в положение равновесия.

Так как площадь диска достаточно велика, вследствие сопротивления воздуха свободные колебания маятника будут быстро затухать. Момент силы сопротивления M_с пропорционален угловой скорости:

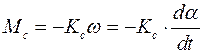, (9.2)

где K_c – коэффициент сопротивления.

В соответствии с основным уравнением динамики вращательного движения твердого тела запишем

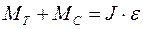, (9.3)

где J – момент инерции маятника;

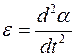– угловое ускорение.

С учетом (9.1) и (9.2) преобразуем (9.3):

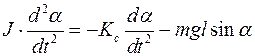или 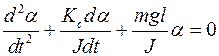, (9.4)

обозначив 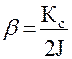, (9.5)

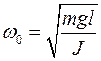, (9.6)

получим дифференциальное уравнение затухающих колебаний физического маятника

(9.7)

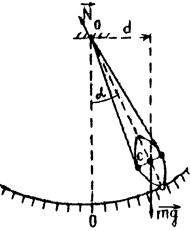
Рис. 9.1

 

Решение данного уравнения можно записать в виде

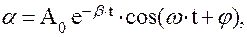(9.8)

где А₀ – амплитуда затухающих колебаний в начальный момент времени;

β – коэффициент затухания;

– циклическая частота затухающих колебаний;

w_o – циклическая частота свободных незатухающих колебаний данной системы;

e – основание натурального логарифма.

Выражение

(9.9)

представляет собой амплитуду затухающих колебаний, значение которой с течением времени будет уменьшаться.

 

Задание 1.Определение периода и частоты колебаний маятника.

 

1. Определить период колебаний T. Для этого по секундомеру замерить время t, за которое маятник совершит 8–13 полных колебаний N. Измерение повторить 3–5 раз. Рассчитать период колебаний по формуле .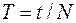

Результаты измерений занести в табл. 9.1.

Таблица 9.1

Измеряемые и расчетные величины для определения периода и частоты физического маятника

  2.По формуле < ω > =определить значение циклической частоты <…

Измеряемые и расчетные величины для определения параметров затухающих колебаний физического маятника

Задание 3. По известному значению периода колебаний и данным (табл. 9.2) построить график затухающих колебаний А = f (T), откладывая значения…  

Контрольные вопросы

 

1. Какой маятник называется физическим?

2. Какие колебания называют затухающими?

3. Какова причина затухания свободных колебаний?

4. Что называется амплитудой затухающих колебаний?

5. Как составляется дифференциальное уравнение затухающих колебаний физического маятника?

6. От каких величин зависит частота затухающих колебаний?

7. Как объяснить физический смысл параметров затухания: коэффициента затухания, логарифмического декремента затухания, добротности, времени релаксации?

 

Литература [5, § 141, 146].

 

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

 

1. Грабовский Р.И. Курс физики / Р.И. Грабовский. – СПб.: Лань, 2002. – 608 с.

2. Савельев И.В. Курс общей физики / И.В. Савельев. – СПб.; М.; Кранодар: Лань, 2005. – 503 с.

3. Трофимова Т.И. Курс физики / Т.И. Трофимова. – М.: Академия, 2006. – 557 с.

ОГЛАВЛЕНИЕ

Введение ........................................................................................................ Общие рекомендации ................................................................................... Классификация ошибок измерения .............................................................. Методика расчета случайных ошибок прямых измерений............................... Лабораторная работа 1. Определение геометрических размеров тела (4 ч) .................................................................................................................... Лабораторная работа 2. Измерение времени и массы (4 ч) ....................... Лабораторная работа 3. Определение массы тела с помощью пружинного маятника (4 ч) ................................................................................... Лабораторная работа 4. Определение коэффициента упругости пружины (4 ч) ........................................................................................................ Лабораторная работа 5. Определение силы земного притяжения с помощью математического маятника (4 ч) .............................................. Лабораторная работа 6. Изучение законов сохранения импульса и энергии при упругом ударе (4 ч) ................................................................. Лабораторная работа 7. Определение момента инерции тела (4 ч) ........... Лабораторная работа 8. Определение момента инерции методом крутильных колебаний (4 ч) ....................................................................... Лабораторная работа 9. Определение параметров затухающих колебаний физического маятника (4 ч) ........................................................... Библиографический список ..........................................................................