рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Физика
- /
- ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Реферат Курсовая Конспект
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ - раздел Физика, ПРАКТИЧЕСКАЯ РАБОТА № 1 УСТАНОВЛЕНИЕ ЗАКОНА ИЗМЕНЕНИЯ СЛУЧАЙНЫХ Испытанием Или Опытом Называют Реализацию Н...
Испытанием или опытом называют реализацию некоторых правил, условий. Например, испытанием будет контроль годности изделий проходными и непроходными калибрами, определение величины размера изделия, обработанного на станке. Явления, получающиеся в результате испытания, называются событиями. Событиями будут: появление бракованного изделия при контроле калибрами, получение определенного размера изделия при его измерении. В теории вероятностей обычно рассматриваются массовые испытания, т. е. испытания, происходящие при неизменных основных условиях неоднократно.
События подразделяются на следующие.
1. Событие называется достоверным, если в результате данного испытания оно обязательно произойдет. Например, появление бракованного экземпляра в партии забракованных изделий будет достоверным событием.
2. Событие называется невозможным, если в результате данного испытания оно произойти не может. Например, появление годного экземпляра в партии негодных изделий будет невозможным событием.
3. Событие называется случайным (или возможным), если в результате данного испытания оно может произойти, но может и не произойти, Например, появление бракованного экземпляра в партии изготовленных изделий при неустановившемся или неизученном технологическом процессе является случайным (или возможным) событием.
4. Два события называются несовместными, если при испытании появление одного из них исключает возможность появления другого. Например, проходимость проходной и непроходной сторон калибра при контроле годной детали есть события несовместные.
5. Два события называются совместными, если при испытании появление одного из них не исключает возможность появления другого. Например, проходимость проходной и непроходной сторон калибра при контроле бракованной детали есть события совместные.
6. События называются единственно возможными, когда при испытании произойдет хотя бы одно из этих событий. Например, при контроле изделий калибрами единственно возможными событиями будут появление или не появление бракованного изделия; для годных изделий единственно возможными событиями являются проходимость через проходной калибр и непроходимость через непроходной калибр.
7. Если при испытании могут появиться несколько возможных событий, и при этом нет основания предполагать, что появление одних возможнее других, то такие события называются равновозможными. Например, партия изделий содержит 10 пронумерованных бракованных изделий. При вынимании из партии у нас нет основания предполагать, что появление того или другого номера бракованного изделия возможнее другого. Появление бракованного изделия с тем или другим номером в данном случае - события равновозможные.
Вероятностью события называется отношение числа случаев, благоприятствующих наступлению данного события, ко всему числу несовместных, единственно возможных и равновозможных событий
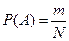 ,
,
где Р (А) - вероятность события А;
m - число случаев, благоприятствующих наступлению события А;
N - число несовместных, единственно возможных и равновозможных событий.
Например, пусть задан допуск на диаметр  . Изделия, выходящие за верхнюю и нижнюю границы допуска, считаются бракованными, а лежащие внутри поля допуска - годными. Положим, что партия, состоящая из N=1000 изделий содержит m1=15 изделий, выходящих за верхнюю границу допуска, и m2=18 изделий, выходящих за нижнюю границу допуска. В этом случае вероятность появления в партии бракованного изделия при испытании будет равна
. Изделия, выходящие за верхнюю и нижнюю границы допуска, считаются бракованными, а лежащие внутри поля допуска - годными. Положим, что партия, состоящая из N=1000 изделий содержит m1=15 изделий, выходящих за верхнюю границу допуска, и m2=18 изделий, выходящих за нижнюю границу допуска. В этом случае вероятность появления в партии бракованного изделия при испытании будет равна
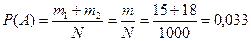
Если m = N, то 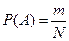 - событие Адостоверно.
- событие Адостоверно.
Если m=0, то Р(А)=0 - событие невозможно.
Случайной величиной называют величину, которая в результате опыта может принимать различные значения. Например, извлечение из партии бракованного изделия есть случайная величина, которая может принимать значение "+" при появлении бракованного изделия, и значение "-" при его не появлении. Величина размера обработанного на станке годного изделия есть также случайная величина, которая может принимать любое значение в пределах заданного поля допуска. Случайные величины обычно обозначают большими буквами, например, Х. Значения случайной величины, которые она принимает в результате опыта, обозначают малыми буквами х1, х2,... хn. При массовых испытаниях каждое из возможных значений случайной величины х1, х2,... хn может встретиться m1, m2,... mn раз. Эти числа называют частотами. Если всего было проведено N испытаний, т.е. , то отношение
, то отношение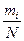 называют частостью или относительной частотой.
называют частостью или относительной частотой.
Совокупность, содержащая все исследуемые изделия, называется генеральной совокупностью. Выбранные из генеральной совокупности N изделий образуют выборку объема N.
Дискретными случайными величинами называют такие, которые могут принимать лишь определенные значения, например: 0,1; 0,2; 0,3 и т. д.
Непрерывными случайными величинами называют такие, которые в некотором интервале могут принимать любое значение.
Число бракованных изделий в различных выборках из генеральной совокупности есть дискретная случайная величина, а размер этих изделий - непрерывная случайная величина.
Дискретная случайная величина задана, если имеется вероятность каждого ее значения (табл. 1).
Таблица 1.
| Х | х1 | х2 | х3 | . . . | хn |
| P (X=xi) | P (х1) | P (х2) | P (х3) | . . . | Р (хn) |
Всякую непрерывную случайную величину можно задать в виде дискретной, если все возможные ее значения разбить на интервалы и задать вероятности появления этих интервалов (из-за ограниченности измерительных средств все замеры непрерывных величин задаются в дискретном виде).
Дадим понятие плотности и интегральной функции распределения случайных величин.
Если Х - случайная величина, а х - некоторое ее значение, то вероятность того, что Х < х равна:
F (x) = P (X < x), (1)
где F (x) - некоторая функция, называемая интегральной функцией распределения (рис. 1). На рис. 1 F(x) - ордината кривой в некоторой точке х. При любом х0 = F(x) = 1.
Плотность вероятности j (х) есть предел отношения вероятности того, что случайная величина Х примет значение, лежащее между х и х + Dх, к величине интервала Dх при Dх®0, т. е.
 (2)
(2)
Функцию j (х) называют также дифференциальным законом распределения.
j(х) и F (х) связаны соотношением
 . (2а)
. (2а)
Будем считать, что случайная величина задана теоретическим законом, если заданы ее интегральный закон или ее плотность вероятности.
Случайная величина задана эмпирическим законом распределения, если для каждого значения случайной величины известна частота встречаемости или частость, полученная из N опытов (табл. 2).

Рис.1
Таблица 2
| Значение Х | х1 | х2 | х3 | . . . | хn |
| Частоты | m1 | m2 | m3 | . . . | mn |
| Частости | m1 N | m2 N | m3 N | . . . | mn N |
При
В пределе частости стремятся к вероятностям соответствующих значений случайной величины.
Всякое теоретическое распределение характеризуется величиной своих основных параметров: математическим ожиданием МХ (центром группирования) и дисперсией DX (величиной рассеивания).
Для дискретной случайной величины (см. табл. 1).
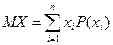 (3)
(3)
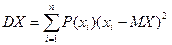 (4)
(4)
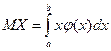 (5)
(5)
 (6)
(6)
Или  (7)
(7)
 (8)
(8)
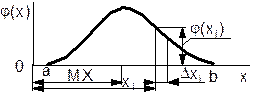
Рис.2




 Формулы (5), (6) применяются для тех случаев, когда случайная величина принимает значения от a до b; формулы (7), (8) - когда X изменяется от - ¥ до ¥.
Формулы (5), (6) применяются для тех случаев, когда случайная величина принимает значения от a до b; формулы (7), (8) - когда X изменяется от - ¥ до ¥.
 называется средним квадратическим отклонением или стандартом.
называется средним квадратическим отклонением или стандартом.
Эмпирическое распределение характеризуется средним значением , равным
, равным
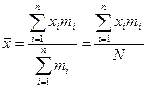 (9)
(9)
или 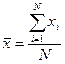 (9a)
(9a)
Среднее значение характеризует центр группирования значений случайной величины. При достаточно большом N
(N ® ¥ ) выборочное значение х стремится по величине к математическому ожиданию, т. е. x » МХ.
Величина рассеивания выборочных значений вокруг их среднего значения характеризуется эмпирической дисперсией S2, равно
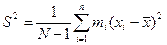 (10)
(10)
Для N ³ 25 вместо формулы (10) пользуются формулой (10а)
 , где
, где 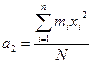 (10а)
(10а)
 называется эмпирическим средним квадратическим отклонением.
называется эмпирическим средним квадратическим отклонением.
При N ® ¥ S2 » DX.
Кроме среднего значения и дисперсии, кривые распределения характеризуются также асимметрией (А) и эксцессом (Е)
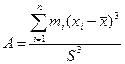 (11)
(11)

Если А = 0, то кривая симметрична. Если А > 0 - кривая имеет положительную асимметрию, а если А < 0 - отрицательную (рис. 3).
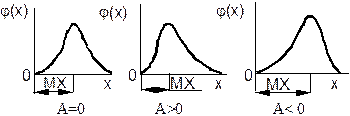
Рис. 3
Эксцесс характеризует крутизну кривой. В качестве кривой с нулевым эксцессом принята кривая нормального распределения, имеющая плотность вероятности
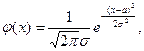 (12)
(12)
где a = MX - математическое ожидание;
s2 - дисперсия.
Если Е > 0, то говорят, что имеется положительный эксцесс, т. е. вершина кривой находится выше кривой нормального распределения. Если Е < 0 - имеется отрицательный эксцесс, и вершина кривой находится ниже вершины кривой нормального распределения (рис. 4).

Рис. 4
Во многих технических приложениях [*], [**], [***] функции распределения характеризуются коэффициентом относительного рассеивания (К), коэффициентом относительной асимметрии (a) и величиной практически предельного поля рассеивания. Дадим определение этих понятий.
Положим, что погрешности отклонений размеров изделий от их номинального значения заданы функцией плотности j (х) и величинами параметров МХ, DX (рис. 5). Примем номинальное значение за начало координат.

Рис. 5
Практически предельным полем рассеивания называется расстояние между такими двумя значениями t1 и t2 случайной величины, при которых площадь, ограниченная кривой, осью абсцисс и отрезком [t1, t2], равна 1 - 2b, где 2b - вероятность риска (брака). Обычно принимают 2b = 0,0027. По определению можно написать
 .
.
На практике обычно t1 и t2 выбирают так, что 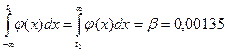
Определенное таким образом практически предельное поле рассеивания принимают за поле допуска, т.е. 2dт = t2 - t1.
Введем обозначения:
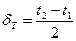 - половина поля допуска,
- половина поля допуска,
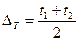 - координата середины поля допуска (рис. 5),
- координата середины поля допуска (рис. 5),
 - коэффициент относительной асимметрии,
- коэффициент относительной асимметрии,
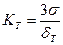 - коэффициент относительного рассеивания, где
- коэффициент относительного рассеивания, где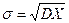 .
.
(индекс “T” при D, d, a, К указывает на теоретическое значение этих коэффициентов. Эти же коэффициенты, определяемые для эмпирических распределений, будут иметь в дальнейшем индекс “э” и обозначаться Dэ, dэ, aэ, Кэ).
В тех случаях, когда целью эксперимента является лишь определение или уточнение значений коэффициентов относительно заданного конструктором поля допуска, не подлежащего пересмотру, коэффициенты aэ и Кэ определяются по формулам: 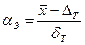 ,
,  .
.
При этом может оказаться, что заданное конструктором поле допуска не соответствует практически предельному полю рассеивания, т. е. вероятность риска (брака) не равна 2b = 0,0027.
____________________________________
* Бородачев Н.А. Анализ качества и точности производства, М., Машгиз, 1961.
** Бородачев Н.А. Основные вопросы теории точности производства, Академиздат, 1950.
*** Вандер Ваден Б.А. Математическая статистика, М. ИЛ, 1960.
Практически предельное поле рассеивания оказывается не равным полю допуска также в тех случаях, когда за величину поля допуска принимается вся зона рассеивания R (величина размаха), равная разности между максимальным и минимальным значениями случайной величины в выборке, т. е. R = xmax - x min.
– Конец работы –
Эта тема принадлежит разделу:
ПРАКТИЧЕСКАЯ РАБОТА № 1 УСТАНОВЛЕНИЕ ЗАКОНА ИЗМЕНЕНИЯ СЛУЧАЙНЫХ
УСТАНОВЛЕНИЕ ЗАКОНА ИЗМЕНЕНИЯ СЛУЧАЙНЫХ... ВЕЛИЧИН ПО РЕЗУЛЬТАТАМ ОПЫТА...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов