СООТНОШЕНИЯ НЕОПРЕДЕЛЕННОСТЕЙ
В координатном представлении
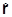 = r,
= r, 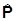 = -iiÑ.
= -iiÑ.
Коммутаторы этих операторов таковы :
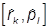 = iidkl
= iidkl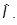
Очевидно, что коммутатор оператора координаты с «чужим» компонентом импульса (скажем, 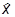 с
с 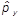 ) равен нулю. Проверим, что
) равен нулю. Проверим, что
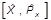 = ii
= ii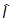 (
( 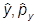 и
и 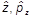 , аналогично ).
, аналогично ).
Имеем:
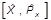 y(x) =
y(x) = 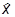
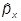 y-
y-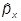
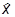 y = x
y = x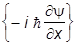 +ii
+ii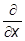 (xy) =
(xy) =
= - ii x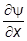 + ii x
+ ii x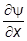 + ii y = ii
+ ii y = ii 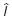 y,
y,
откуда в силу произвольности y и получаем, что надо.
Итак, коммутатор координаты со «своим» импульсом отличен от нуля. Это накладывает ограничения на дисперсии координаты и импульса в заданном состоянии, называемые соотношениями неопределенностей. Проведем общее рассмотрение для наблюдаемых A и B, записывая
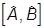 = i
= i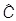 ,
,
где 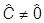 . Операторы
. Операторы 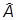 и
и 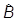 эрмитовы, и множитель i введен для того, чтобы оператор
эрмитовы, и множитель i введен для того, чтобы оператор 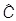 был также эрмитовым (сам коммутатор антиэрмитов). Введем операторы уклонения от среднего значения в заданном состоянии:
был также эрмитовым (сам коммутатор антиэрмитов). Введем операторы уклонения от среднего значения в заданном состоянии:
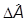 º
º 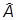 -
-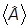
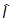 ,
, 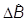 º
º 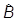 -
-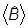
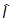 .
.
Они эрмитовы и удовлетворяют тому же коммутационному соотношению:
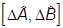 = i
= i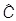 .
.
Дисперсией наблюдаемой A (аналогично B) в состоянии y называется
Dy(A) º (DA)2 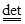
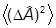 .
.
Задача - получить ограничения на дисперсии наблюдаемых A и B.
Образуем скалярное произведение (D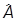 y,D
y,D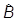 y) и найдем его мнимую часть:
y) и найдем его мнимую часть:
Im(D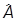 y, D
y, D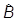 y) = 1/2i{ (D
y) = 1/2i{ (D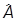 y, D
y, D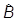 y) - (D
y) - (D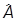 y, D
y, D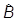 y)* }=
y)* }=
= 1/2i{( D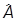 y, D
y, D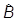 y)-( D
y)-( D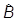 y, D
y, D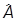 y)} =
y)} =
= 1/2i{( y, D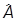 D
D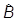 y)-( y, D
y)-( y, D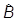 D
D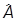 y)} =
y)} =
= 1/2i (y,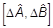 y) = 1/2i(y,
y) = 1/2i(y,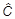 y) = 1/2áCñ.
y) = 1/2áCñ.
Учтем теперь, что модуль мнимой части не больше модуля самого числа, а затем воспользуемся неравенством Коши - Буняковского:
| Im(D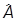 y, D
y, D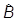 y)| £ | (D
y)| £ | (D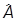 y, D
y, D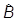 y)| £
y)| £ 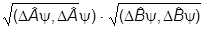 =
=
= 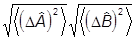 =
= 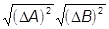 º (DA)(DB).
º (DA)(DB).
Сравнивая с предыдущим, мы и приходим к общему соотношению неопределенностей:
DA×DВ l 1/2UáCñU.
В частности, для координаты и импульса 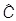 = i
= i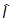 , а потому áCñ = i, и получаем соотношение неопределенностей Гейзенберга:
, а потому áCñ = i, и получаем соотношение неопределенностей Гейзенберга:
DxDpx l i/2.
Ни в одном состоянии дисперсии координаты и импульса не могут обе быть нулями. Значит x и px совместно неизмеримы.