КАРТИНЫ ШРЕДИНГЕРА И ГЕЙЗЕНБЕРГА
Зависимость от времени можно ввести в квантовую механику разными способами. Они называются разными картинами (представлениями).
До сих пор мы пользовались картиной Шредингера, в которой считается, что всю зависимость от времени несут векторы состояния (волновые функции), а в операторы наблюдаемых она может входить лишь в исключительных случаях (например, в гамильтониан системы, находящейся в нестационарных внешних условиях). Основным динамическим уравнением в картине Шредингера является уравнение Шредингера.
ii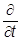 |yш(t)ñ =
|yш(t)ñ = 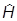 ш |yш(t)ñ.
ш |yш(t)ñ.
Оно позволяет связать вектор состояния |yш(t)ñ в произвольный момент времени t с вектором состояния |yш(t0)ñ, заданным в начальный момент 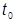 . Ведем оператор эволюции
. Ведем оператор эволюции 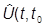 ) определением
) определением
|yш(t)ñ = 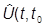 )|yш(t0)ñ.
)|yш(t0)ñ.
Так как нормировка векторов не должна меняться во времени, имеем:
1 = áyш(t0)Uyш(t0) ñ = áyш(t)Uyш(t) ñ = áyш(t0) 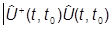 | yш(t0) ñ,
| yш(t0) ñ,
т.е. 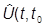 ) должен быть унитарным оператором:
) должен быть унитарным оператором:
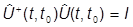 .
.
Если гамильтониан 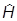 не зависит явно от времени (стационарные внешние условия), то оператор эволюции может быть выписан в явном виде:
не зависит явно от времени (стационарные внешние условия), то оператор эволюции может быть выписан в явном виде:
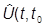 ) =
) = 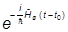
Тогда
|yш(t)ñ = 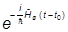 .
.
Дифференцируя это соотношение по времени, найдем::
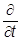 |yш(t)ñ =- i/i×
|yш(t)ñ =- i/i×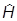 ш
ш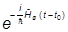 =- i/i×
=- i/i×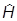 ш |yш(t)ñ
ш |yш(t)ñ 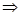 ii
ii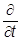 | yш(t)ñ =
| yш(t)ñ = 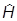 ш |yш(t)ñ,
ш |yш(t)ñ,
т.е. получим уравнение Шредингера, как и должно быть.
Перейдем теперь к картине Гейзенберга, совершая унитарное преобразование
|yг(t)ñ = 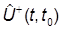 |yш(t)ñ =
|yш(t)ñ = 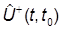
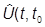 )|yш(t0)ñ =
)|yш(t0)ñ =
= 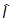 |yш(t0)ñ = |yш(t0)ñ
|yш(t0)ñ = |yш(t0)ñ
т.е.
|yг(t)ñ = |yш(t0)ñ = |yг(t0)ñ º |yгñ.
Таким образом, в картине Гейзенберга векторы состояний не меняются во времени: один и тот же вектор описывает состояние системы во все моменты времени.
Но теперь вся зависимость от времени перекидывается на операторы наблюдаемых, унитарное преобразование которых дает
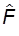 г(t) =
г(t) = 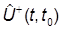
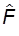 ш
ш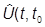 ) .
) .
При унитарном преобразовании средние значения наблюдаемых не меняются. Их в разных картинах можно записать как
áFñ (t) = áyш(t) U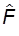 ш |yш(t) ñ =
ш |yш(t) ñ =
= áyгU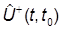
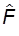 ш
ш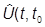 )|yгñ = áyгU
)|yгñ = áyгU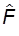 г(t) |yгñ.
г(t) |yгñ.
Таким образом, зависимость от времени средних значений не зависит от выбора картины, а именно она-то и является самой главной.
В картине Гейзенберга уравнения Шредингера нет, так как векторы состояний постоянны. Основные динамические уравнения формулируются для операторов. Чтобы получить их, найдем сначала уравнение, которому подчиняется оператор эволюции и сопряженный ему. Имеем:
|yш(t) ñ = 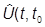 )|yш(t0) ñ.
)|yш(t0) ñ.
Дифференцируем по времени:
ii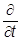 |yш(t) ñ = ii
|yш(t) ñ = ii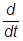
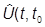 )|yш(t0) ñ.
)|yш(t0) ñ.
С другой стороны, согласно уравнению Шредингера,
ii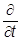 |yш(t) ñ =
|yш(t) ñ = 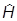 ш |yш(t0) ñ =
ш |yш(t0) ñ = 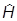 ш
ш 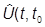 |yш(t0) ñ.
|yш(t0) ñ.
Сравнение дает уравнение
ii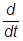
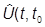 ) =
) = 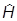 ш
ш 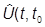 ),
),
к которому нужно добавить очевидное начальное условие
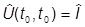 .
.
Переходя к сопряженному уравнению с учетом эрмитовости 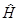 найдем
найдем
- ii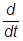
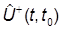 =
= 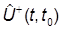
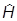 ш
ш
Гамильтониан в КГ имеет вид
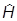 г =
г = 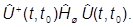
Если
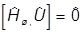 ,
,
то мы выносим 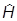 ш налево и пользуемся унитарностью
ш налево и пользуемся унитарностью 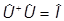 . Тогда получим
. Тогда получим
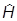 г (t) =
г (t) = 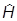 ш º
ш º 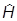 .
.
Это справедливо, в частности, когда 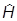 ш не зависит от времени и (см. выше)
ш не зависит от времени и (см. выше)
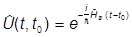 .
.
Очевидно, что в этом случае 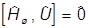 .
.
Теперь, пользуясь уравнениями для 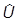 и
и 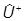 , мы можем получить динамические уравнения для операторов наблюдаемых в картине Гейзенберга:
, мы можем получить динамические уравнения для операторов наблюдаемых в картине Гейзенберга:
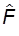 г(t) =
г(t) = 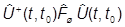 .
.
Дифференцируем по времени:
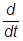
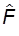 г(t) =
г(t) =
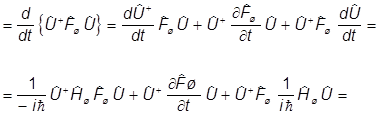
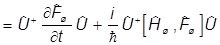 .
.
В итоге получаем уравнения Гейзенберга - динамические уравнения в картине Гейзенберга:
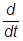
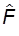 г(t)
г(t) 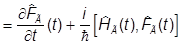 ,
,
где по определению
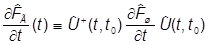 .
.
Картина Шредингера хороша при практической работе (уравнения для векторов состояний в определенном представлении становятся дифференциальными уравнениями для обычных функций - волновых функций). Картина Гейзенберга с этой точки зрения хуже (уравнения для операторов), но она хороша при общих размышлениях. В частности, позволяет с легкостью обсудить законы сохранения.