ОРБИТАЛЬНЫЙ МОМЕНТ ИМПУЛЬСА
Дальше мы намерены перейти к анализу движения частицы в центральном поле. Как и в классической физике, здесь очень важную роль играет момент импульса. Но в квантовой механике бывает два момента импульса - связанный с движением частицы и имеющий классический аналог, и не связанный с движением частицы, собственный момент, не имеющий классического аналога. Первый называется орбитальным, второй - спином. Сейчас будем рассматривать только орбитальный момент импульса.
В классической механике
L= r´p.
Эта формула переносится и в квантовую механику, но для операторов:
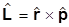
В декартовых координатах в r-представлении компоненты имеют вид:
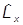 =
=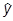
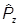 -
- 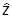
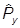 = -i
= -i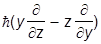
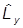 =
=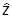
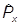 -
-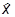
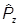 = -i
= -i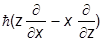
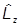 =
=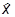
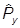 -
-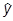
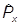 = -i
= -i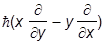 .
.
Это можно записать единообразно:
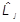 = i
= i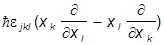 .
.
Здесь ejkl --символ Леви-Чевита: антисимметричен по всем индексам и нормирован условием e123 = +1. Компоненты с разными значками отличны от нуля, а если хотя бы одна пара одинаковых индексов, то равны 0. При этом
e123 = e312 = e231 = +1, e213 = e321 = e132 = -1.
Используя коммутации
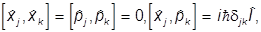
легко показать, что
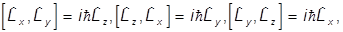
т.е.
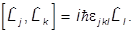
Важную роль играет оператор квадрата момента
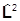 =
=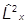 +
+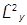 +
+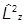 ,
,
который коммутирует с операторами компонентов момента:
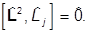
Дальнейший анализ удобно проводить в сферических координатах
x = rcosjsinq, y =rsinjsinq, z =rcosq.
Довольно нудные выкладки по замене переменных дают:
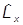 = i
= i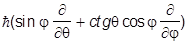
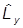 = -i
= -i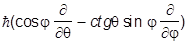
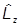 = -i
= -i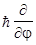 .
.
Особенно важным является последнее соотношение. Проверим его
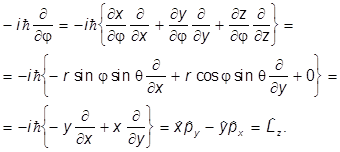
Не менее важен оператор 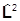 .
.
В сферических координатах он с точностью до множителя совпадает с угловой частью оператора Лапласа:
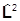 =
= 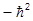 Ñq,j2 = -
Ñq,j2 = -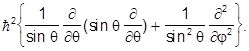
Напомним, что полный оператор Лапласа есть
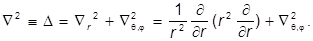
Все операторы момента содержат только q и j, но не r. Поэтому их собственные функции могут содержать любую зависимость от r, которая нас не интересует. Считаем поэтому, что все происходит на сфере единичного радиуса, а потому
y = y(q,j).
Ставим задачу на отыскание общих собственных функций взаимно коммутирующих операторов 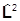 и
и 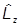 :
:
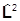 y(q,j) = L2y(q,j)
y(q,j) = L2y(q,j)
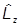 y(q,j) = Lzy(q,j)
y(q,j) = Lzy(q,j)
и вводим обозначения
L2 = l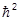 , Lz = m
, Lz = m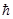 ,
,
так что в явном виде уравнения запишутся как
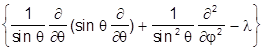 y(q,j) = 0
y(q,j) = 0
-i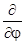 y(q,j) = my(q,j).
y(q,j) = my(q,j).
Решения должны быть: непрерывными, конечными и однозначными. В курсе математической физики доказывается, что решения нашей задачи существуют только при
l = l(l+1), где l = 0,1.2,...
и m =m, где m- целые числа из интервала -l£ m £l.
Таким образом, каждому неотрицательному целому l отвечает 2l+1 независимых решения с разными m.
Они называются сферическими функциями (гармониками) и имеют вид
ylm(q,j) = Ylm(q,j) =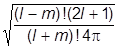 Plm(cosq)eimj,
Plm(cosq)eimj,
присоединенные полиномы (хотя и не полиномы) Лежандра
Plm(z) = (1-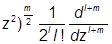 (z2-1)l, m>0.
(z2-1)l, m>0.
и выражаются через обычные полиномы Лежандра:
Plm (z) = (1-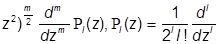 (z2-1)l.
(z2-1)l.
Сферические гармоники образуют ортонормированную систему функций на сфере единичного радиуса:
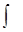 dWY lm* (q,j)Yl’m’(q,j) = dll’dmm’,
dWY lm* (q,j)Yl’m’(q,j) = dll’dmm’,
где
dW = sinqdqdj
есть элемент телесного угла (или элемент площади сферы с R=1). Кроме того, на этой сфере они образуют базис, так что
y(q,j) = 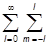 ClmYlm(q,j), Clm =
ClmYlm(q,j), Clm =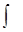 dWY lm* (q,j)y(q,j).
dWY lm* (q,j)y(q,j).
Сферические функции обладают свойством
 Y lm* (q,j) = (-1)m Y lm (q,j).
Y lm* (q,j) = (-1)m Y lm (q,j).
Итак, мы установили, что орбитальный момент квантуется. Квадрат его принимает значения
L2 = 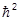 l(l+1), l = 0,1,2,...
l(l+1), l = 0,1,2,...
а проекция на ось z - значения
Lz = 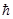 m, -l £ m £ l
m, -l £ m £ l