ДВИЖЕНИЕ В ЦЕНТРАЛЬНОМ ПОЛЕ
Центральное поле - это такое, для которого
V = V(r),r º ïrï.
Гамильтониан
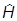 =
= 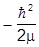 Ñ2 +V(r)
Ñ2 +V(r)
записываем в сферических координатах. Учитывая, что
Ñ2 = Ñr2 +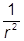 Ñjq2,
Ñjq2,
и вспоминая, что
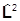 = -
= -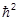 Ñjq2,
Ñjq2,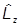 = -i
= -i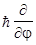 ,
,
получим
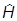 =
= 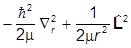 +V(r).
+V(r).
Отсюда видно, что
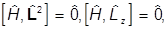
поскольку 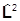 и
и 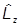 не включают
не включают 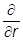 , а потому коммутируют с V(r), и поскольку
, а потому коммутируют с V(r), и поскольку
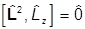 .
.
Таким образом, энергия, квадрат момента импульса и его проекция совместно измеримы. Поэтому они имеют общие собственные функции. Таковые и будем искать. Так как собственные функции 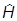 - решения стационарного уравнения Шредингера:
- решения стационарного уравнения Шредингера:
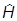 y(r,q,j) = Ey(r,q,j),
y(r,q,j) = Ey(r,q,j),
то ищем решения с определенными L2 и Lz:
y = yE,l,m(r,q,j),
где l характеризует L2, m характеризует Lz.
Но общие собственные функции 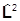 и
и 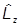 нам известны - при фиксированном r (на сфере) это сферические гармоники Y lm (q,j):
нам известны - при фиксированном r (на сфере) это сферические гармоники Y lm (q,j):
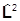 Y lm (q,j) =
Y lm (q,j) = 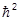 l(l+1) Y lm (q,j),
l(l+1) Y lm (q,j), 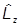 Y lm (q,j) =
Y lm (q,j) = 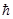 m Y lm (q,j).
m Y lm (q,j).
Поэтому ищем решения в виде:
yE,l,m(r,q,j) = fElm(r) Y lm (q,j).
Подставляем в уравнение
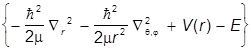 yE,l,m(r,q,j) = 0,
yE,l,m(r,q,j) = 0,
учитывая, что вся угловая зависимость входит только в 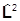 :
:
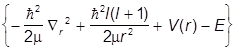 fElm(r) = 0,
fElm(r) = 0,
(на сферическую функцию сократили). В это уравнение m не входит, а потому радиальные функции от m не зависят:
fElm(r) = fEl(r).
Логика, которая приводит к данному результату, такова: задача сферически симметрична, отсюда нет выделенных направлений, отсюда волновые функции стационарных состояний фактически не зависят от проекции момента m (точнее, от m не зависит энергия, а значит радиальная часть волновой функции).
Итак, для радиальной волновой функции получаем уравнение
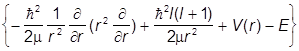 fEl(r) = 0.
fEl(r) = 0.
Удобно сделать замену неизвестной функции, вводя
REl(r) = rfEl(r).
Для функции REl(r) получаем уравнение
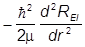 +
+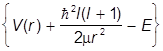 REl = 0.
REl = 0.
По форме оно очень похоже на одномерное уравнение Шредингера
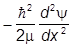 + [V(x) - E]y = 0,
+ [V(x) - E]y = 0,
но есть два существенных отличия:
· теперь задача ставится на полупрямой (0, +¥), а не на всей прямой, и граничное условие нужно задавать не только на бесконечности, но и в точке r=0;
· потенциальная энергия заменяется на эффективную потенциальную энергию
Vэфф(r) = 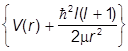 º Vl(r),
º Vl(r),
(сравн. с классической механикой).