МОМЕНТ ИМПУЛЬСА
Мы уже рассмотрели свойства момента импульса одной частицы, который был связан с ее движением в пространстве и определялся как
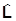 =
= 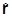 ´
´ 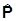
Это есть орбитальный момент. Теперь мы хотим обобщить это понятие, для чего получим его несколько иным способом - из симметрийных соображений.
Рассматриваем систему нескольких частиц с волновой функцией
y(r1,...rN) º y(ra).
Произведем вращение системы координат на угол dj (вектор dj)направлен по оси вращения, а его модуль равен углу поворота). Это означает, что физическая система осталась той же самой, а приборы повернулись на угол dj. Радиусы- векторы изменятся:
r¢a = ra + dra , dra=dj´ra.
Преобразуются и значения y - функции, но так как в «новую» точку ra «придет» «старая» точка ra -dra,то должно быть
y¢(ra) = y(ra-dra).
Разлагая в ряд Тейлора, найдем:
y¢(ra) = y(ra-dra) = y(ra) -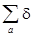 ra
ra 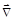 ay(ra) = (
ay(ra) = (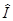 -
-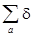 ra
ra 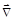 a) y(ra)
a) y(ra)
= (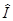 -
-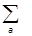 (dj´ra)
(dj´ra)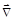 a) y(ra) = (
a) y(ra) = (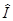 -dj
-dj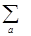 ra
ra 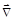 a) y(ra) º
a) y(ra) º
º (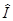 -
-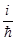 dj
dj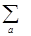 ra ´ (-i
ra ´ (-i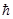
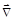 a)) y(ra) = (
a)) y(ra) = (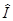 -
- 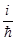 dj
dj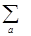
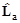 )y(ra).
)y(ra).
Итак,
y¢(ra) = (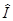 -
-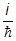 dj
dj 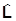 )y(ra), (*),
)y(ra), (*),
где
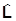 =
=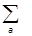
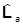 =
=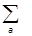
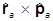 (**)
(**)
В данном случае мы ничего нового не получили. Но важно, что момент импульса можно трактовать двумя способами. Согласно определению (*), оператор 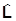 описывает преобразование волновой функции при малом вращении, т.е.
описывает преобразование волновой функции при малом вращении, т.е. 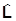 является генератором вращения. Согласно определению (**) оператор
является генератором вращения. Согласно определению (**) оператор 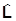 выражается через координаты и импульсы так же, как в классической механике. Еще раз: в данном случае получилось, что это одно и то же. Но в общей ситуации определение (*) может оказаться более общим. Оператор (**) действует только на координаты волновой функции. Но у нее могут быть и другие какие-то переменные, на которые (**) не действует, а (*) - действует.
выражается через координаты и импульсы так же, как в классической механике. Еще раз: в данном случае получилось, что это одно и то же. Но в общей ситуации определение (*) может оказаться более общим. Оператор (**) действует только на координаты волновой функции. Но у нее могут быть и другие какие-то переменные, на которые (**) не действует, а (*) - действует.
И такие дополнительные переменные действительно существуют у многих частиц (прежде всего у электрона). Это - спиновые переменные, являющиеся внутренними, врожденными степенями свободы частицы, никак не связанными с координатами. Обозначая их буквой s, запишем волновую функцию одной частицы как
y = y(r,s),
и в полной аналогии с рассмотренным частным случаем введем по определению оператор полного момента импульса как генератор вращений, т.е. преобразующий волновую функцию по закону
y¢(r,s) = (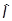 -
- 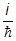 dj
dj )y(r,s).
)y(r,s).
Оператор  можно представить в виде двух слагаемых:
можно представить в виде двух слагаемых:
 =
=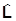 +
+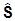 .
.
Оператор 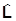 есть рассмотренный ранее оператор орбитального момента, который действует только на координаты. Оператор
есть рассмотренный ранее оператор орбитального момента, который действует только на координаты. Оператор 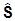 есть новый оператор - оператор спина, который действует только на спиновые переменные s. Оператор спина можно определить как оператор
есть новый оператор - оператор спина, который действует только на спиновые переменные s. Оператор спина можно определить как оператор  ,действующий в системе покоя частицы. Значит это действительно внутренний, врожденный момент импульса частицы.
,действующий в системе покоя частицы. Значит это действительно внутренний, врожденный момент импульса частицы.
Найдем правила коммутации  с операторами других физических величин. Пусть физическая величина F- векторная, и ей соответствует векторный оператор
с операторами других физических величин. Пусть физическая величина F- векторная, и ей соответствует векторный оператор  . Установим закон преобразования среднего значения Fпо произвольному состоянию y. С одной стороны имеем:
. Установим закон преобразования среднего значения Fпо произвольному состоянию y. С одной стороны имеем:
dF ºdá ñy = áy¢ê
ñy = áy¢ê êy¢ñ-áyê
êy¢ñ-áyê êyñ »
êyñ »
áyê(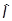 +
+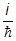 dj
dj )
) (
(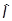 –
– 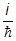 dj
dj )êyñ @
)êyñ @ 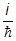 áyê[dj
áyê[dj ,
, ]êyñ.
]êyñ.
С другой стороны, как и для всякой векторной величины,
dF = dj´F = djáyê êyñ = áyêdj´
êyñ = áyêdj´ êyñ.
êyñ.
Сравнение дает
[ ,dj
,dj ] = i
] = i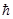 dj´
dj´ .
.
Проектируем на ось 1:
[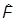 1,dj1
1,dj1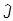 1+dj2
1+dj2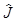 2 + dj3
2 + dj3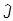 3] = i
3] = i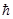 (dj2
(dj2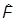 3-dj3
3-dj3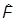 2).
2).
Сравниваем коэффициенты при dj1, а потом при dj2 :
[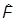 1,
1,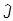 1]=0, [
1]=0, [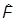 1,
1,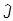 2] = i
2] = i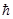
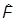 3.
3.
Остальные случаи получаются проектированием на оси 2 и 3, или циклической перестановкой индексов в выписанных соотношениях:
[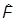 j,
j,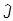 k] = i
k] = i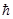 ejkl
ejkl 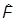 l.
l.
В частности, полагая  =
= ,получим коммутационные соотношения для компонентов самого момента:
,получим коммутационные соотношения для компонентов самого момента:
[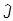 j,
j,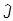 k] = i
k] = i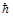 ejkl
ejkl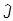 l.
l.
Так как  =
=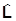 +
+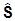 , [
, [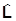 ,
,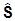 ]=
]=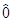 (действуют на разные переменные) и
(действуют на разные переменные) и
[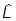 j,
j,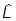 k] = i
k] = i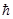 ejkl
ejkl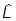 l
l
то для спиновых операторов получаем те же коммутационные соотношения, что и для орбитальных:
[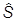 j,
j,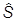 k] = i
k] = i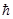 ejkl
ejkl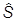 l.
l.
Если оператор F-скалярный, то абсолютно аналогичные рассуждения, основывающиеся на том, что при вращении dF = 0, дают
[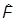 ,
,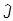 k] =
k] = 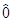 .
.
В частности, для квадратов полного момента и спина получаем
[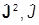 k] =
k] = 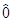 Þ [
Þ [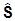 2,
2,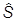 k]=
k]=