Движение частицы в потенциальном ящике конечной глубины
 Рассмотрим поведение частицы в потенциальном ящике конечной глубины. Потенциальная энергия частицы в ящике
Рассмотрим поведение частицы в потенциальном ящике конечной глубины. Потенциальная энергия частицы в ящике  при
при  , вне ящика (
, вне ящика ( )
)  (рис.5.6).
(рис.5.6).
Примером такой ситуации является движение коллективизированных электронов внутри металла (согласно классической электронной теории вне металла потенциальная энергия электрона равна нулю, а внутри металла она отрицательна и равна 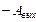 ).
).
 Применим к частице в таком потенциальном ящике уравнение Шредингера (будем считать, что задача одномерная, тогда
Применим к частице в таком потенциальном ящике уравнение Шредингера (будем считать, что задача одномерная, тогда  ) .
) .
В области I  .
.
В области II 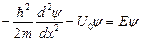 ,
,
или
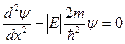 при
при 
 при
при 
(Е<0, т.к. потенциальная энергия 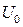 отрицательна и превышает кинетическую, в противном случае частица выйдет из ящика). Нам нужно найти волновые функции
отрицательна и превышает кинетическую, в противном случае частица выйдет из ящика). Нам нужно найти волновые функции 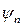 и энергии
и энергии  , которые бы удовлетворяли граничному условию такому, что
, которые бы удовлетворяли граничному условию такому, что 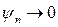 при
при 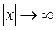 .
.
Из классической теории следует, что 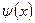 должна обращаться в ноль при
должна обращаться в ноль при  т.к.
т.к. 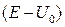 в этой области отрицательна, что соответствует отрицательным значениям кинетической энергии, запрещенным в классической физике, однако в этой области (I) уравнение Шредингера имеет решение:
в этой области отрицательна, что соответствует отрицательным значениям кинетической энергии, запрещенным в классической физике, однако в этой области (I) уравнение Шредингера имеет решение:

где 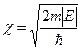 , или
, или 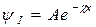 .
.
В области II (при 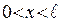 ) решение уравнения Шредингера дает:
) решение уравнения Шредингера дает: 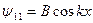 , где
, где  , k имеет смысл волнового числа волны де Бройля. При
, k имеет смысл волнового числа волны де Бройля. При 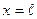
 или
или 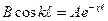 .
.
Поведение  - функции при п=1 показано на рисунке 5.7.
- функции при п=1 показано на рисунке 5.7.  - функция не падает скачком до нуля при
- функция не падает скачком до нуля при 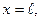 как это было в случае ящика с бесконечно высокими стенками.
как это было в случае ящика с бесконечно высокими стенками.
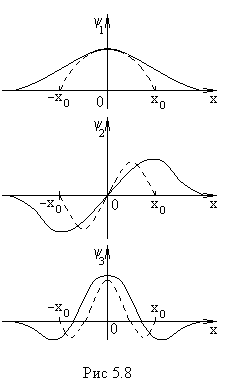
Это означает, что существует вероятность для частицы выйти из ямы, когда ее энергия Е меньше глубины ямы  . На рис.5.8 сплошными линиями изображены стоячие волны низшего порядка, соответствующие энергиям
. На рис.5.8 сплошными линиями изображены стоячие волны низшего порядка, соответствующие энергиям 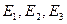 . Штриховые линии - соответствующие волновые функции в потенциальной яме той же ширины, но с бесконечно высокими стенками.
. Штриховые линии - соответствующие волновые функции в потенциальной яме той же ширины, но с бесконечно высокими стенками.
Решение задачи о частице в потенциальной яме имеет практические значения. Короткодействующие ядерные силы, действующие между электроном и протоном, можно представить в виде прямоугольной потенциальной ямы и найти энергию связи.