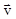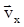Радиус вектор, перемещение, траектория, путь. Вектор скорости, модуль вектора скорости. Уравнение пути
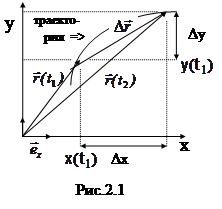
Начнем изучение механики с механики материальной точки. Положение точки удобно задать в прямоугольной системе координат. Система координат должна быть определенным, известным способом связана с телами отсчета. Для простоты будем рассматривать плоское движение, т.е. двумерную систему координат. Положение точки определяется координатами xи y.Вектор проведенный из начала координат в точку называется радиус-вектором точки (рис.2.1). Из рисунка 2.1 видно, что проекции вектора r на оси координат равны:
|

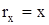 ;
;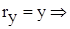
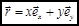 (2.1)
(2.1)
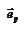 ( В дальнейшем для упрощения орты на чертежах изображать не будем). При движении точка “описывает” некоторую линию она называется траектори-ей. Длина траектории называется длиной пути (или короче - путь). Вектор, соединяющий начальное положение точки ( положение в момент времени
( В дальнейшем для упрощения орты на чертежах изображать не будем). При движении точка “описывает” некоторую линию она называется траектори-ей. Длина траектории называется длиной пути (или короче - путь). Вектор, соединяющий начальное положение точки ( положение в момент времени 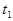 ) и конечное ( в момент времени
) и конечное ( в момент времени 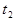 ) называется перемещением. На рисунке 2.1 это вектор D
) называется перемещением. На рисунке 2.1 это вектор D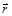 :
:
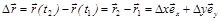
Средним вектором скорости 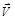 за время
за время  называется вектор равный:
называется вектор равный:
 (2.2)
(2.2)
Мгновенной скоростью называется величина равная
 (2.3)
(2.3)
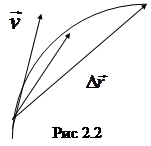
Таким образом, мгновенная скорость равна производной от радиус-вектора по времени. Т.к. при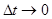 вектор
вектор 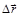 стремится установиться по направлению касательной (рис. (2.2)), то из (2.2) и (2.3) следует, что вектор
стремится установиться по направлению касательной (рис. (2.2)), то из (2.2) и (2.3) следует, что вектор 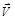 направлен по касательной к траектории.
направлен по касательной к траектории.
Подставим в (2.3) выражение (2.1)
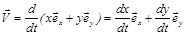 (2.4)
(2.4)
|
Выразим вектор 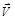 через его проекции
через его проекции 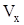 ,
, 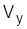 :
:
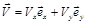 (2.5)
(2.5)
Из сравнения уравнений (2.4) и (2.5) видно, что проекции вектора скорости равны соответствующим производным от координат:
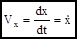 ;
;  (2.6)
(2.6)
Найдем модуль вектора скорости, исходя из (2.3) :

Из рис. (2.2) видно, что модуль вектора D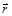 , т.е. его длина, стремиться к длине дуги траектории, которая “ограничивает“ вектор. Следовательно, при
, т.е. его длина, стремиться к длине дуги траектории, которая “ограничивает“ вектор. Следовательно, при 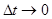
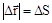 , т.е. равен пути, которую проходит частица за время Dt. Таким образом, получаем:
, т.е. равен пути, которую проходит частица за время Dt. Таким образом, получаем:
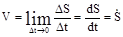 (2.7)
(2.7)
Модуль вектора скорости равен производной от пути по времени. Модуль вектора скорости можно так же найти, зная его проекции
(рис. 2.3).
| |||
| |||




|



 S
S





 за время
за время 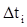
Рис.2.3
Выразим путь ,предполагая, что известна скорость V(t) (рис.2.3). Интервал времени от 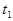 до
до 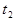 разобьем на малые промежутки
разобьем на малые промежутки 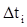 . Тогда из (2.7) следует:
. Тогда из (2.7) следует:
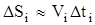
Весь путь S равен : 
Чем меньше все промежутки 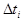 , тем точнее мы найдем путь:
, тем точнее мы найдем путь:
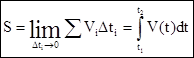 (2.8)
(2.8)
Отметим, что уравнение (2.8) можно получить просто математически из (2.7): dS = V(t) dt , проинтегрируем это равенство, считая, что при 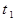 S = 0, а при
S = 0, а при 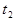 путь равен S:
путь равен S:
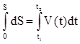 . Т.к.
. Т.к.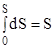 , то получим уравнение (2.8)
, то получим уравнение (2.8)
Из свойств интегралов следует, что путь равен площади под графиком скорости.
Пример. Равномерным движением называется такое движение, при котором модуль скорости V постоянен (не меняется). Если V = const , то в интеграле (2.8) V можно вынести за знак интеграла:
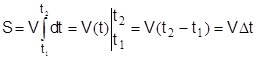
( если 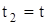 , а
, а  ).
).