Закон Дальтона.
Рассмотрим газовую смесь, состоящую из n-компонентов. Обозначим 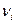 - количество молей i-той константы смеси,
- количество молей i-той константы смеси,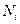 - число молей i-той константы.
- число молей i-той константы.
Давление, которое оказывал бы какой-либо из газов (констант) в отсутствии всех остальных компонентов называется парциальным давлением этого газа.
Согласно определению парциальное давление i-той константы этого газа равно: 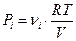 .
.
Тогда суммы парциальных давлений газов, входящих в смесь равна соответственно 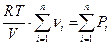 . (*)
. (*)
С другой стороны, согласно уравнению состояния идеального газа 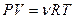 , где
, где
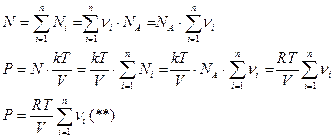
Сопоставляя (*) и (**)
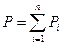
Давление смеси газов равно сумме парциальных давлений газовых компонент, входящих в смесь – закон Дальтона.
§23. Барометрическая формула.
Распределение Больцмана
Рассмотрим каким образом ведёт себя идеальный газ в поле силы тяжести Земли. Выделим для этого мысленно в газе вертикальный столб с площадью поперечного сечения S.
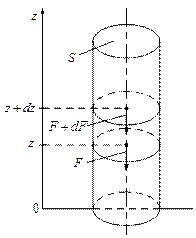
| Выделим из этого столба бесконечно тонкий слой dz.
Силу, с которой газ, находящийся выше, давит на нижнее основание слоя на высоте z обозначим за F, на высоте  за за  . Приращение силы . Приращение силы 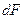 равно весу газа внутри слоя, взятому с обратным знаком, т.к. с высотой величина давления силы уменьшается. равно весу газа внутри слоя, взятому с обратным знаком, т.к. с высотой величина давления силы уменьшается. 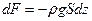
|
Тогда приращение давления 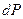 , вызванное действием силы тяжести, будет
, вызванное действием силы тяжести, будет  . Из уравнения Клапейрона-Менделеева
. Из уравнения Клапейрона-Менделеева  выразим плотность
выразим плотность 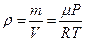 , тогда
, тогда 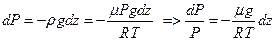 , положим
, положим 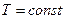
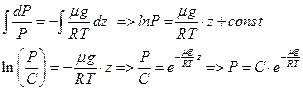
Обозначим давление при z=0 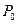
 - данное выражение называется барометрической формулой и показывает зависимость давления идеального газа от высоты при постоянной температуре газа.
- данное выражение называется барометрической формулой и показывает зависимость давления идеального газа от высоты при постоянной температуре газа.
Используя соотношение, что  , запишем барометрическую формулу для концентрации.
, запишем барометрическую формулу для концентрации.
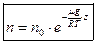 , где
, где 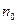 - концентрация у поверхности Земли.
- концентрация у поверхности Земли.
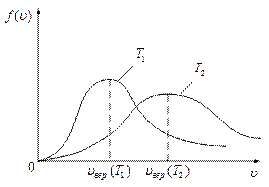
Изобразим эту зависимость графически для двух газов, имеющих одинаковую концентрацию молекул 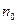 у поверхности Земли, но разные молекулярные массы
у поверхности Земли, но разные молекулярные массы 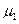 и
и 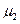 .
.
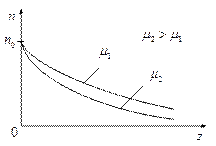
| Эта зависимость показывает, что газ являющийся смесью газов с увеличением высоты обогащается более лёгкими компонентами. |
Такое утверждение справедливо и для нашей воздушной атмосферы. Верхние слои атмосферы обеднены кислородом и обогащены водородом, и в горах трудно дышать из-за нехватки кислорода, а не из-за перепада давления.
Барометрическую формулу можно использовать для расчёта высоты полёта летательных аппаратов, измеряя давление на борту и зная его у поверхности Земли, вводя поправку на изменение температуры. Предназначенный для этой цели барометр, проградуированный в значениях высоты, называется альтиметр.
Учитывая, что 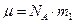 , а
, а 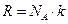 барометрическую формулу для концентрации можно записать
барометрическую формулу для концентрации можно записать
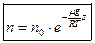 .
.
Однако, учитывая что  , где П - потенциальная энергия молекулы в поле силы тяжести Земли, то можно записать барометрическую формулу так (
, где П - потенциальная энергия молекулы в поле силы тяжести Земли, то можно записать барометрическую формулу так (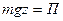 )
)
 (***)
(***)
Больцман показал, что записанная формула (***) справедлива в случае потенциального силового поля любой природы для совокупности любых одинаковых частиц, находящихся в состоянии хаотического теплового движения при постоянной температуре. В связи с этим зависимость концентрации частиц от их потенциальной энергии называется функция распределения Больцмана (распределение по координатам).
В общем случае потенциальная энергия частицы является функцией трёх её координат, в силу чего и концентрация является функцией координат:
 ,
,
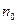 - концентрация в точках, где
- концентрация в точках, где 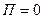 .
.
В заключении отметим, что число частиц 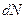 в элементарном объёме пространства
в элементарном объёме пространства 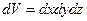 в близи точки с координатами
в близи точки с координатами 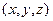 равно
равно
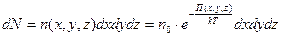 .
.
§24. Распределение Максвелла
Это распределение молекул газа по скоростям. Рассуждение не строгое на основе аналогий.
Распределение Больцмана даёт возможность определить концентрацию молекул газа в зависимости от их потенциальной энергии, однако логично предположить, что подобное распределение молекул и для кинетической энергии поступательного движения молекул газа.
Но если потенциальная энергия есть функция координат молекулы, то её кинетическая энергия (есть функция координат скорости 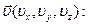
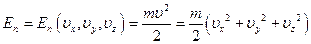
В силу этого величина концентрации является функцией координат вектора скорости 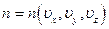 , то есть речь идёт о концентрации молекул в пространстве скоростей.
, то есть речь идёт о концентрации молекул в пространстве скоростей.
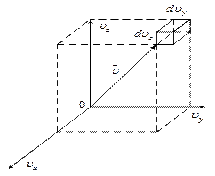
| Пространство скоростей задаётся тремя взаимно ортогональными осями 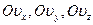 , имеющими общую точку О. Положение молекулы в любой момент времени в ней определяется координатами , имеющими общую точку О. Положение молекулы в любой момент времени в ней определяется координатами 
|
вектора скорости в данный момент времени, то есть вектор электронов в пространстве скоростей выполняет роль радиус-вектора в обычном пространстве.


Элементарный объём пространства скоростей 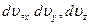 , тогда число частиц в этом объёме
, тогда число частиц в этом объёме
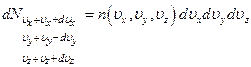

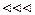
По аналогии с распределением Больцмана можно предположить:

Определим постоянную С, учитывая, что общее число молекул газа во всём пространстве скоростей равно N.
Суммирование всех молекул сводится к интегрированию по всему пространству скоростей
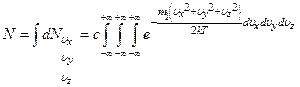
Такое интегрирование с учётом того, что 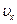 не зависит от
не зависит от  и
и  , сводится к перемножению трёх интегралов
, сводится к перемножению трёх интегралов

Все три интеграла равны друг другу. Достаточно определить один из них.
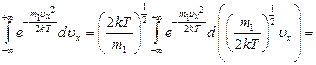
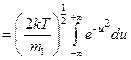 - интеграл Пуассона
- интеграл Пуассона
 , получаем
, получаем
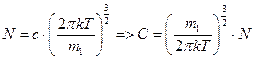
Таким образом, число молекул в элементарном объёме пространства скоростей будет равно
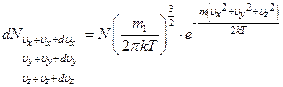


Или концентрация в пространстве скоростей равна

Если концентрацию в пространстве скоростей умножить на элементарный объём шарового слоя радиуса  толщиной
толщиной 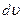 , в пределах такого слоя величину концентрации можно считать постоянной, то мы получим число молекул, лежащих внутри такого слоя.
, в пределах такого слоя величину концентрации можно считать постоянной, то мы получим число молекул, лежащих внутри такого слоя.
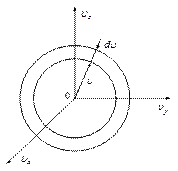
| dN - число молекул, модуль скорости которых лежит в интервале от  до до 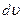 . Объём такого шарового слоя очевидно равен . Объём такого шарового слоя очевидно равен  . .
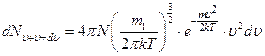
|
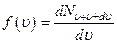 - функция распределения Максвелла.
- функция распределения Максвелла.

§25. График функции распределения Максвелла. Расчёт наиболее вероятной средней арифметической и средней квадратичной скоростей с помощью функции распределения Максвелла
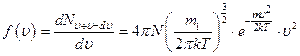
Сначала выясним, что при 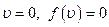 , а при
, а при  .
.
Найдём экстремум этой положительной функции.
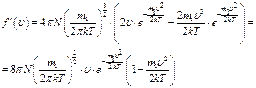
В области  функция имеет единственный экстремум, являющийся максимумом в силу положительности функции
функция имеет единственный экстремум, являющийся максимумом в силу положительности функции 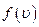 . Значение скорости, при которой он наблюдается, называется наиболее вероятной скоростью
. Значение скорости, при которой он наблюдается, называется наиболее вероятной скоростью
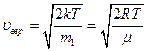
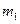 - масса одной молекулы.
- масса одной молекулы.
С ростом температуры 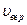 увеличивается, а
увеличивается, а 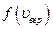 - уменьшается.
- уменьшается.
Построим с учётом сказанного график функции 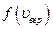 :
:  и
и 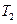 (
(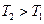 ).
).
Площадь под этой кривой равна 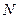 , а
, а  - площадь под кривой в интервале этих скоростей.
- площадь под кривой в интервале этих скоростей.
Используя функцию распределения Максвелла, можно определить среднее значение модуля скорости молекул газа - 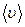 , которое есть среднее арифметическое скоростей молекул.
, которое есть среднее арифметическое скоростей молекул.
Для того, чтобы понять, как это можно сделать, обратимся сначала к случаю дискретного распределения некоторых частиц по скорости.
Пусть 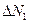 - число частиц, обладающих скоростью
- число частиц, обладающих скоростью 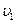 ,
, 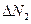 - число частиц, обладающих скоростью
- число частиц, обладающих скоростью 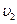 ,
,  -
-  . Тогда среднее арифметическое абсолютного значения скорости частиц равно:
. Тогда среднее арифметическое абсолютного значения скорости частиц равно:
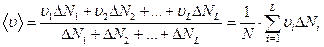 .
.
В случае непрерывного распределения молекул газа по скоростям (т.е. в случае очень большого количества частиц) сумма в предыдущем выражении заменяется интегралом.
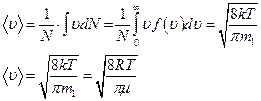
Аналогично, можно найти среднее значение квадрата скорости молекул газа
 .
.
Учитывая это, получим что
 .
.
Этим результатом мы воспользовались ранее при выводе уравнения идеального газа (т.е. логически следовало бы выводить сначала распределение Максвелла, а следом уравнение состояния идеального газа).
Величина, равная 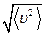 , равна
, равна 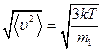 и именуется средней квадратичной скоростью.
и именуется средней квадратичной скоростью.

На графике функции распределения Максвелла отметим эти скорости.

§26. Внутренняя энергия идеального газа.
Закон равнораспределения газа
по степеням свободы молекулы
Под внутренней энергией тела понимают сумму всех видов энергии, заключённой в теле, без учёта энергии взаимодействия и движение тела как целого, т.е. энергия взаимодействия тела с другими телами, а также кинетическая энергия, соответствующая движению всего тела, не входят в понятие внутренняя энергия.
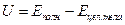 - внутренняя энергия тела.
- внутренняя энергия тела.
Внутренняя энергия: 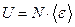 , где
, где 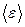 - средняя энергия одной молекулы, N - общее число молекул в газе.
- средняя энергия одной молекулы, N - общее число молекул в газе.
В общем случае молекулы участвуют в поступательном, вращательном и колебательном движениях.

Опр.
Числом степеней свободы молекулы называется минимальное число независимых величин, необходимых для однозначного определения (задания) положения молекулы в пространстве.
1) Положение материальной точки в пространстве определяется значением трёх её координат 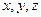 , таким образом число степеней свободы материальной точки как и одноатомной молекулы равно трём.
, таким образом число степеней свободы материальной точки как и одноатомной молекулы равно трём.
2) В двухатомной молекуле, атомы которой не перемещаются друг относительно друга, число степеней свободы – 5: 3 координаты её центра масс и 2 угла поворота вокруг двух взаимно перпендикулярных осей.
3) У абсолютно твёрдого тела как у трёх- и более атомных молекул, атомы которых не лежат вдоль одной прямой линии, будет 6 степеней свободы: 3 координаты центра масс и 3 угла поворота вокруг взаимно перпендикулярных осей.
При поступательном движении молекулы изменяются только 3 декартовых координаты её центра масс, поэтому говорят, что 3 степени свободы, связанные с движение центра масс молекулы являются поступательными; изменение параметров, связанных с вращением молекулы называется вращательными степенями свободы (у двухатомной молекулы - 2; у многоатомной нелинейной - 3).
Но если атомы в молекуле связаны друг с другом нежёстко, то говорят, что существуют наравне с поступательными и вращательными ещё и колебательные степени свободы.
4) Если 2 атома в молекуле связаны упруго, то они связаны тремя координатами центра масс, двумя углами поворота вокруг взаимно перпендикулярных осей (двумя вращательными степенями свободы) и расстоянием между атомами, которое может меняться, и является колебательной степенью свободы.
5) N-атомная нелинейная молекула с упругими связями обладает:
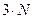 степенями свободы, т.к. каждый атом обладает тремя степенями свободы: число поступательных –3, вращательных -2, колебательных –
степенями свободы, т.к. каждый атом обладает тремя степенями свободы: число поступательных –3, вращательных -2, колебательных –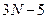 .
.
6) N-атомная линейная молекула с упругими связями обладает 3N степенями свободы: поступательных-3, вращательных 3, колебательных: 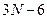 .
.
На каждую из поступательных степеней свободы приходится в среднем одинаковая кинетическая энергия, равная 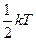 (на все 3 степени свободы приходится
(на все 3 степени свободы приходится  )
)
Закон:
Согласно закону равнораспределения на каждую степень свободы молекулы (поступательную, вращательную, колебательную) в среднем приходится одинаковая кинетическая энергия, равная 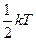 .
.
На колебательную степень свободы кинетической энергии приходится ещё и в среднем такое же количество потенциальной энергии (наподобие сжатой пружины, суммарная энергия которой состоит из равных средней кинетической и потенциальной энергий).
Колебательная степень свободы молекулы таким образом обладает по сравнению с поступательной и вращательной степенями свободы удвоенной энергетической ёмкостью.
Из закона равнораспределения кинетической энергии по степеням свободы вытекает, что средняя энергия одной молекулы определяется формулой:
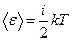 , где
, где 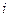 - называемое числом степеней свободы есть сумма
- называемое числом степеней свободы есть сумма  .
.
Тогда:  ;
;
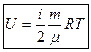 .
.
§27. Работа газа при изменении его объёма.
Первое начало термодинамики