Квадратные, треугольные, диагональные, симметрические матрицы. Единичная матрица.
Занятие 1. Матрицы. Операции над матрицами.
1.1. Операции с матрицами: равенство матриц; умножение матрицы на число; сложение матриц; перемножение матриц. Основные свойства операций сложения и умножения матриц.
1.2. Транспонирование матрицы.
1.3. Квадратные, треугольные, диагональные, симметрические матрицы. Единичная матрица.
1.4. Возведение квадратной матрицы в натуральную степень.
Сначала вспомним определение матрицы. Матрица – прямоугольная таблица чисел, содержащая 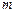 строк и
строк и  столбцов, записанная в круглых скобках или двойных прямых чертах.
столбцов, записанная в круглых скобках или двойных прямых чертах.
Пример 1.
1)  - матрица размером
- матрица размером 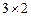 , содержащая 3 строки и 2 столбца.
, содержащая 3 строки и 2 столбца.
2) 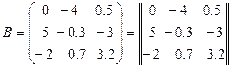 - матрица размером
- матрица размером 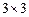 .
.
3)  - матрица размером
- матрица размером  . Матрицу с одним столбцом часто называют вектор-столбцом.
. Матрицу с одним столбцом часто называют вектор-столбцом.
4) 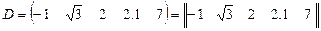 - матрица размером
- матрица размером  . Матрицу с одной строкой также называют вектор-строкой.
. Матрицу с одной строкой также называют вектор-строкой.
Элементы матрицы 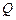 обозначаются
обозначаются 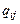 , где первый индекс
, где первый индекс 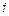 означает номер строки,
означает номер строки,  - номер столбца, на пересечении которых стоит соответствующий элемент. Так в примере 1 для матриц
- номер столбца, на пересечении которых стоит соответствующий элемент. Так в примере 1 для матриц 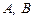 имеем
имеем
 , где
, где 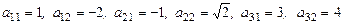 .
.
 , где
, где  .
.
1.1. Операции над матрицами.
1.1.1. Равенство матриц. Матрица  равна матрице
равна матрице  , если у обеих матриц одинаковые размеры и
, если у обеих матриц одинаковые размеры и  , т.е. совпадают соответствующие элементы этих матриц для всех возможных наборов индексов
, т.е. совпадают соответствующие элементы этих матриц для всех возможных наборов индексов 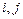 .
.
Пример 2.
1)  .
.
2) 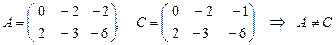 , т.к.
, т.к. 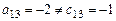 .
.
3) 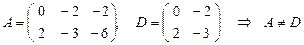 , т.к. матрицы
, т.к. матрицы  имеют различные размеры.
имеют различные размеры.
1.1.2. Умножение матрицы на число
на число  происходит по правилу:
происходит по правилу:
 , где
, где 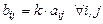 .
.
Пример 3.
1)  .
.
2) 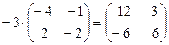 .
.
1.1.3. Сложение матриц  и
и  возможно только для матриц с одинаковыми размерами и производится по правилу:
возможно только для матриц с одинаковыми размерами и производится по правилу:  , где
, где 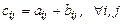 .
.
Пример 4.
1)  .
.
2)  .
.
Операции сложения матриц и умножение матриц на число обладают следующими свойствами:
 - свойство коммутативности сложения матриц;
- свойство коммутативности сложения матриц;
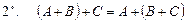 - свойство ассоциативности сложения матриц;
- свойство ассоциативности сложения матриц;
 - первый закон дистрибутивности;
- первый закон дистрибутивности;
 - второй закон дистрибутивности.
- второй закон дистрибутивности.
1.1.4. Нахождение разности 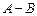 матриц
матриц 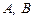 определяется с помощью рассмотренных выше операций умножения матрицы на число и сложения матриц:
определяется с помощью рассмотренных выше операций умножения матрицы на число и сложения матриц: 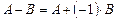 . Аналогично,
. Аналогично, 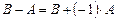 .
.
Пример 5.
1)  .
.
2)  .
.
1.1.5. Перемножение матриц.Матрицу  можно умножить слева на матрицу
можно умножить слева на матрицу  (или матрицу
(или матрицу  можно умножить справа на матрицу
можно умножить справа на матрицу  ) и, тем самым, найти произведение
) и, тем самым, найти произведение  только тогда, когда число столбцов левой матрицы
только тогда, когда число столбцов левой матрицы  равно числу строк правой матрицы
равно числу строк правой матрицы  . Если под матрицами написать их размеры, то
. Если под матрицами написать их размеры, то
 , (1)
, (1)
где
 . (2)
. (2)
Формула (1) показывает, какие размеры будет иметь матрица 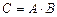 , а формула (2) определяет правило, по которому находятся элементы матрицы
, а формула (2) определяет правило, по которому находятся элементы матрицы  . Говорят также, что элемент
. Говорят также, что элемент 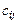 матрицы
матрицы 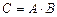 есть результат «скалярного произведения»
есть результат «скалярного произведения» 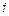 -й строки матрицы
-й строки матрицы  на
на  -й столбец матрицы
-й столбец матрицы  .
.
Пример 6.Найти  и
и  , если
, если  .
.
1)  .
.
 (скалярному произведению 1-й строки матрицы
(скалярному произведению 1-й строки матрицы  на 1-й столбец матрицы
на 1-й столбец матрицы )=
)=
= ,
,
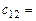 (скалярному произведению 1-й строки матрицы
(скалярному произведению 1-й строки матрицы  на 2-й столбец матрицы
на 2-й столбец матрицы )=
)=
= ,
,
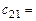 (скалярному произведению 2-й строки матрицы
(скалярному произведению 2-й строки матрицы  на 1-й столбец матрицы
на 1-й столбец матрицы )=
)=
=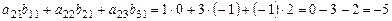 ,
,
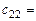 (скалярному произведению 2-й строки матрицы
(скалярному произведению 2-й строки матрицы  на 2-й столбец матрицы
на 2-й столбец матрицы )=
)=
=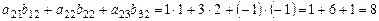 .
.
Следовательно,  .
.
2)
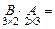
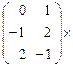

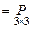
 (скалярному произведению 1-й строки матрицы
(скалярному произведению 1-й строки матрицы  на 1-й столбец матрицы
на 1-й столбец матрицы  )=
)=
= ,
,
 (скалярному произведению 1-й строки матрицы
(скалярному произведению 1-й строки матрицы  на 2-й столбец матрицы
на 2-й столбец матрицы  )=
)=
=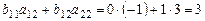 ,
,
 (скалярному произведению 1-й строки матрицы
(скалярному произведению 1-й строки матрицы  на 3-й столбец матрицы
на 3-й столбец матрицы  )=
)=
= ,
,
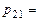 (скалярному произведению 2-й строки матрицы
(скалярному произведению 2-й строки матрицы  на 1-й столбец матрицы
на 1-й столбец матрицы  )=
)=
= ,
,
 (скалярному произведению 2-й строки матрицы
(скалярному произведению 2-й строки матрицы  на 2-й столбец матрицы
на 2-й столбец матрицы  )=
)=
=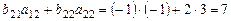 ,
,
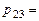 (скалярному произведению 2-й строки матрицы
(скалярному произведению 2-й строки матрицы  на 3-й столбец матрицы
на 3-й столбец матрицы  )=
)=
=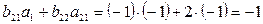 ,
,
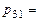 (скалярному произведению 3-й строки матрицы
(скалярному произведению 3-й строки матрицы  на 1-й столбец матрицы
на 1-й столбец матрицы  )=
)=
=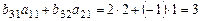 ,
,
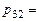 (скалярному произведению 3-й строки матрицы
(скалярному произведению 3-й строки матрицы  на 2-й столбец матрицы
на 2-й столбец матрицы  )=
)=
= ,
,
 (скалярному произведению 3-й строки матрицы
(скалярному произведению 3-й строки матрицы  на 3-й столбец матрицы
на 3-й столбец матрицы  )=
)=
=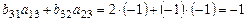 .
.
Следовательно,  .
.
Операции умножения матриц и сложения матриц имеют следующие свойства:
 - свойство коммутативности умножения матриц в общем случае
- свойство коммутативности умножения матриц в общем случае
не выполняется(это видно уже из примера 6);
 - свойство ассоциативности умножения матриц;
- свойство ассоциативности умножения матриц;
 - первый закон дистрибутивности;
- первый закон дистрибутивности;
 - второй закон дистрибутивности.
- второй закон дистрибутивности.
1.2. Транспонирование матрицы. Транспонирование матрицы  обозначается
обозначается 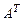 и означает операцию переписывания строк (столбцов) матрицы
и означает операцию переписывания строк (столбцов) матрицы  в виде соответствующих столбцов (строк).
в виде соответствующих столбцов (строк).
Пример 7.
1) 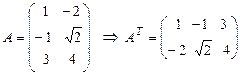 .
.
2)  .
.
3)  .
.
Отметим, что 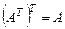 .
.
1.3. Квадратные, треугольные, диагональные, симметричные матрицы. Единичная матрица.
Матрица называется квадратной, если число строк и столбцов в ней одинаково.
Примеры квадратных матриц:
1)  - матрица с размерами
- матрица с размерами 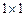 - квадратная матрица 1-го порядка;
- квадратная матрица 1-го порядка;
2)  - матрица с размерами
- матрица с размерами 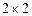 - квадратная матрица 2-го порядка;
- квадратная матрица 2-го порядка;
3)  - квадратная матрица 3-го порядка.
- квадратная матрица 3-го порядка.
Элементы 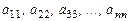 квадратной матрицы
квадратной матрицы 
 -го порядка образуют главную диагональэтой матрицы. Квадратная матрица называется треугольной, если под ее главной диагональю (или над ее главной диагональю) все элементы равны нулю.
-го порядка образуют главную диагональэтой матрицы. Квадратная матрица называется треугольной, если под ее главной диагональю (или над ее главной диагональю) все элементы равны нулю.
Примеры треугольных матриц:
 ,
,  - верхне-треугольные матрицы 2-го и 3-го порядка соответственно;
- верхне-треугольные матрицы 2-го и 3-го порядка соответственно;
 - нижне-треугольные матрицы 3-го и 4-го порядка соответственно.
- нижне-треугольные матрицы 3-го и 4-го порядка соответственно.
Квадратная матрица  называется диагональной,если все элементы
называется диагональной,если все элементы 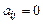 при
при  .
.
Примеры диагональных матриц:
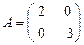 ,
,  ,
,  - диагональные матрицы 2-го, 3-го и 4–го порядка соответственно.
- диагональные матрицы 2-го, 3-го и 4–го порядка соответственно.
Для диагональных матриц 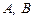 выполнен закон коммутативности умножения матриц
выполнен закон коммутативности умножения матриц  .
.
Квадратная матрица 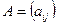 называется симметрической, если
называется симметрической, если 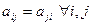 или другими словами
или другими словами 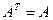 .
.
Например,
 ,
,  симметрические матрицы.
симметрические матрицы.
Единичными матрицами называются диагональные матрицы, у которых все диагональные элементы равны единице. Эти матрицы обычно обозначаются буквой 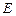 .
.
Примеры единичных матриц:
 ,
,  ,
, 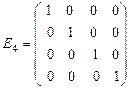 - единичные матрицы 2-го, 3-го и 4–го порядка соответственно. Эти матрицы получили такое название в связи с тем, что для любой матрицы
- единичные матрицы 2-го, 3-го и 4–го порядка соответственно. Эти матрицы получили такое название в связи с тем, что для любой матрицы  размера
размера  выполнены равенства
выполнены равенства  и
и 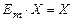 . Если же
. Если же  - квадратная матрица порядка
- квадратная матрица порядка  , то
, то  .
.
Пример 8.Проверить, что  .
.
1)  .
.

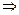
 .
.
2) 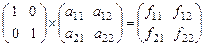 .
.

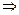
 .
.
1.4. Возведение квадратной матрицы в натуральную степень.
По определению,  .
.
Пример 9.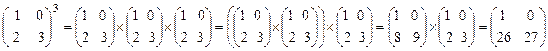 .
.
Домашнее задание.
1. Для заданных матриц 
найти 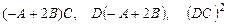 .
.