Понятие предела функции

Понятие предела является фундаментальным в математическом анализе. С его помощью вводятся понятия производной, интеграла, непрерывности и т.д.

Пусть функция f(x) определена в некоторой окрестности X точки a, кроме, быть может, самой точки a.

Определение 1(определение по Коши): Число b называется пределом функции f(x) при х®а, если для любого числа ε > 0, которое может быть сколь угодно малым, существует окрестность точки а, в которой при всех допустимых значениях x ≠ a выполняется |f(x) – b| < ε.

Точка а – точка прикосновения множества D (допустимых значений x), т.е. точка, в любой окрестности которой находятся значения x, кроме, быть может, самой точки a.

Другая формулировка определения предела: Число b называется пределом функции f(x) в точке а (при х®а), если для любого сколь угодно малого ε > 0 существует такое зависящее от ε число δ(ε)>0, что при всех х ≠ a, удовлетворяющих условию 0 < |х – а| < δ, выполняется неравенство |f(x) – b| < ε.

Запись определения предела с помощью логических символов (кванторов):

Здесь: - символ равносильности; символ 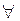- вместо фразы «для любого», - «найдется (существует)», : - «такое, что».

Геометрический смысл предела функции в точке a (рис.1).

Рис.1

Построим график функции у = f(x), точки х = а, у = b (рис.1). Возьмем произвольное сколь угодно малое число ε > 0 и построим на оси OY ε-окрестность относительно числа b: (b-ε; b+ε) и проведем прямые у = b + ε, у = b – ε. Число b будет пределом функции f(x) при х®а, если на оси ОХ найдется такая δ-окрестность точки а (a-δ; a+δ), при попадании в которую значений аргумента х часть графика функции f(x) попадает внутрь полосы, ограниченной ε-окрестностью числа b.

При уменьшении числа ε интервал (b-ε; b+ε) будет стягиваться к числу b. Соответствующий ему интервал (a-δ; a+δ) будет стягиваться к числу a. Это и доказывает, что .

Дадим в общих словах понятие предела функции непрерывного аргумента у=f(х) в точке a.

Пределом функции f(х) называется число b, к которому она стремится при стремлении аргумента x к числу a, если значения f(х) сколь угодно близко приближаются к числу b, когда значения переменной x сколь угодно близко приближаются к числу a.

Обозначение предела: .

В этом определении рассматриваются значения x, сколь угодно близкие к числу a, но не совпадающие с a. Это означает, что точка a имеет δ-окрестность малой величины такую, что 0<|х-а|<δ.

Проиллюстрируем понятие предела функции на примере.

Пример 1. Рассмотрим функцию f(х)=х². Нужно узнать, к чему стремится (не равна!) функция при x → 2.

Запишем предел: и посмотрим на график (рис.2). Проведем параллельно 0Y линию через точку 2 на оси 0X. Она пересекает график в точке М(2; 4). Опустив из этой точки на ось 0Y перпендикуляр, получим значение 4. К этому числу и стремится функция f(х)=х² при x → 2. Заметим, что для нахождения предела необходимо просто подставить в функцию f(х)=х² значение 2 и ответ будет таким же.

Рис.2

Пример 2. Доказать, что .

Решение. Функция f(x)=2х+1 определена всюду (на всей числовой оси), включая точку a=1, в которой f(1)=3.

Согласно определению |f(x)-b|<ε, рассмотрим для любого ε > 0 неравенство |(2х+1) - 3| < ε (здесь b=3).

Оно эквивалентно неравенству |2(х - 1)| < ε или |х - 1| < ε/2.

Таким образом, для любого ε > 0 существует такое число δ=ε/2 (для ε = 0,1 δ=0,05; для ε = 0,01 δ=0,005 и т.д.), что для всех х ≠ 1 и удовлетворяющих условию |х - 1| < δ=ε/2 будет справедливо неравенство |f(x) - 3| = |(2х+1) - 3| < ε. Это и означает, что .

Пример 3. Доказать, что .

Решение. Функция f(x)=х+1 определена всюду, включая точку a=2, в которой f(2)=3.

Согласно определению |f(x)-b|<ε, рассмотрим неравенство

|(х+1) - 3| < ε или |х - 2| < ε. Таким образом, для любого ε > 0 можно взять δ=ε. Тогда для всех х, удовлетворяющих неравенству |х - 2| < δ, будет справедливо неравенство |(х+1) - 3| = < ε. Это и означает, что .