рефераты конспекты курсовые дипломные лекции шпоры
Реферат Курсовая Конспект
Принцип замены эквивалентных
Принцип замены эквивалентных - Лекция, раздел Механика, РАЗДЕЛ 1. Дифференциальное исчисление Если Функции α(Х) И β(Х) Являются Бесконечно Малыми П...
Если функции α(х) и β(х) являются бесконечно малыми при х®а, и если α(х) ~ γ(х), β(х) ~ η(х), то 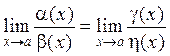 .
.
Пример 5. Вычислить предел, используя принцип замены эквивалентных:
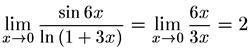 .
.
Пример 6. Найти  .
.
Решение. Заменим ax – 1 ~ x · lna. Тогда  .
.
Определение 3. Если отношение 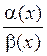 двух бесконечно малых величин само бесконечно мало (
двух бесконечно малых величин само бесконечно мало (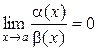 ), то α(х) называется величиной более высокого порядка малости, чем β(х), а β(х) – величиной более низкого порядка малости, чем α(х).
), то α(х) называется величиной более высокого порядка малости, чем β(х), а β(х) – величиной более низкого порядка малости, чем α(х).
В этом случае записывают: 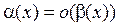 , где символ «о» (символ Ландау) называется «о»-малое.
, где символ «о» (символ Ландау) называется «о»-малое.
Из определения предела для 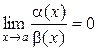 следует, что
следует, что 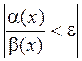 в некоторой δ-окрестности точки а, или
в некоторой δ-окрестности точки а, или 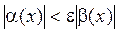 . Говорят, что α(х) имеет более низкий порядок роста, чем β(х). Тогда запишем последнее выражение в виде
. Говорят, что α(х) имеет более низкий порядок роста, чем β(х). Тогда запишем последнее выражение в виде 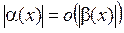 . Рассматривая функцию α(х) как бесконечно малую более высого порядка по сравнению с β(х) при х → а, можем пренебречь знаками обеих функций: изменение знака не приводит к изменению порядка функции. Поэтому модули можно снять, и тогда:
. Рассматривая функцию α(х) как бесконечно малую более высого порядка по сравнению с β(х) при х → а, можем пренебречь знаками обеих функций: изменение знака не приводит к изменению порядка функции. Поэтому модули можно снять, и тогда: 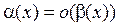 .
.
Пример 7.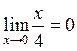 , поэтому х = о(4) при х → 0.
, поэтому х = о(4) при х → 0.
Свойства символа «о»-малое
1.  .
.
2. 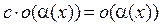 , где с = const ≠ 0.
, где с = const ≠ 0.
3. Если 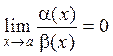 , то
, то  .
.
4. 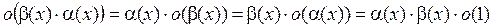 .
.
5. Если 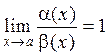 , то
, то 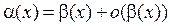 . Последняя запись означает, что к функции β(х) прибавляется некоторая другая функция, о которой известно только то, что она является бесконечно малой более высокого порядка по сравнению с β(х).
. Последняя запись означает, что к функции β(х) прибавляется некоторая другая функция, о которой известно только то, что она является бесконечно малой более высокого порядка по сравнению с β(х).
Если две различные функции α(х) и β(х) удалось представить в виде
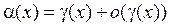 ,
,
 ,
,
то это не означает, что α(х) = β(х), так как под видом о(γ(х)) в этих двух случаях могут скрываться разные бесконечно малые функции.
С использованием символа «о» запись для эквивалентных можно представить в виде асимптотического равенства, например:
sin(x) = x + o(x) при х → 0,
(1 + х)p – 1 = px + o(x) при х → 0.
Пример 6. Докажем последнее асимптотическое равенство, т.е. надо показать, что 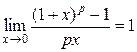 .
.
Решение. Положим (1 + х)p – 1 = y. Очевидно, что y → 0 при х → 0.
Тогда (1 + х)p = y + 1,
откуда
p·ln(1 + х) = ln(y + 1).
Поэтому
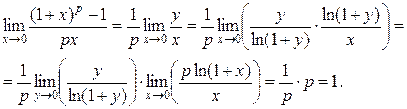
– Конец работы –
Эта тема принадлежит разделу:
РАЗДЕЛ 1. Дифференциальное исчисление
Лекции и Предел функции Понятие предела функции Пусть функция... Свойства бесконечно больших величин... Произведение бесконечно большой величины на функцию имеющую ненулевой предел бесконечно большая величина...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Принцип замены эквивалентных
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов