Непрерывность функции. Точки разрыва функции

В понятии предела при х → х₀ считается, что х ≠ х₀. Если же функция существует в этой точке х₀, то это обстоятельство в определении предела не учитывается.

Теперь рассмотрим случай, когда f(х₀) существует, причем .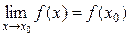

Итак, пусть функция у = f(x) определена в точке х = х₀. Тогда говорят, что функция непрерывна, если для точек х, близких к точке х₀, значения f(x) и f(х₀) также близки друг к другу. Смысл утверждения «если х близко к х₀, то f(x) близко к f(х₀)» можно записать с помощью символов: «если х → х₀, то f(x) → f(х₀)».

Определение 1. Функция f(x) называется непрерывной в точке х = х₀, если предел этой функции при х → х₀ совпадает со значением функции в этой точке: .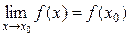

Таким образом, функция f(x) является непрерывной в точке х₀, если выполняются три условия:

1) f(x) существует в точке х₀;

2) f(x) имеет предел в точке х₀;

3).

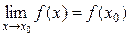Определение непрерывности функции позволяет менять местами символы предела lim и функции f. Действительно, так как , то для непрерывной в точке x = х₀ функции можно записать: .

Это дает основание сформулировать следующее правило: Если функция f(x) непрерывна в точке х₀, то при вычислении предела функции при х → х₀ надо вместо х в выражение f(x) подставить х₀. Полученное число и является пределом функции f(x) в точке х = х₀.

Можно также сказать, что функция у=f(x) является непрерывной в точке х=х₀, если в этой точке отсутствует разрыв функции. Рассмотрим несколько случаев.

1) Функция у=f(x) имеет односторонние пределы: конечный предел справа =f(х₀+0) и конечный предел слева = f(х₀ – 0). Допустим, что эти пределы равны, но значение функции в точке х = х₀ не существует (эта точка на кривой у=f(x) «выколота»), т.е. f(х₀ + 0) = f(х₀ – 0) ≠ f(х₀). Говорят, что функция в точке x = x₀ имеет устранимый разрыв (можно эту точку в кривую «вставить») (рис.1).

Рис.1

 

Определение 2. Точка x = x₀ – точка устранимого разрыва, если предел функции f(x) в этой точке существует, но функция в ней либо не определена, либо значение f(х₀) функции в точке x₀ не равно пределу функции в этой точке: .

Подобный разрыв можно устранить, если дополнить разрывную функцию до непрерывности так:

Пример 1. Функция f(x) = 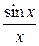в точке x = 0 не является непрерывной, так как нарушено 1-е условие непрерывности – существование f(0), в самой точке x=0 эта функция не определена. Однако f(x) имеет предел, равный единице: 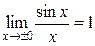. Поэтому точка x = 0 – точка устранимого разрыва. Этот разрыв можно устранить, если доопределить функцию в этой точке значением предела в ней, т.е. ввести новую функцию

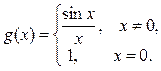
Эта функция g(x) является непрерывной на всей числовой прямой.

Пример 2. Исследовать непрерывность функции в точке x = 0 (рис.2). В точке x = 0 эта функция не определена, значит, функция не является непрерывной. Точка x = 0 – точка устранимого разрыва, так как .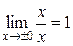

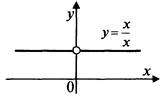
Рис.2

Пример 3. В точке x = 0 функция y = |sign x| не является непрерывной (рис.3). Первые два условия непрерывности выполнены, поскольку

f(0) = |sign(0)| = 0,

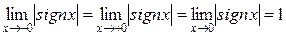, (x = 0 – точка устранимого разрыва).

но нарушено 3-е условие: .

Рис.3

2) Пусть конечные пределы функции у = f(x) в точке x = x₀ и справа, и слева существуют, но они не равны, т.е. f(х₀ + 0) ≠ f(х₀ – 0). Функция в этой точке делает «скачок» (рис.4). Точка x=x₀ в этом случае называется точкой неустранимого разрыва 1-го рода.

Рис.4

Определение 3.Точка x = x₀ – точка разрыва 1-го рода функции f(x), если в этой точке функция имеет конечные, но не равные друг другу левый и правый пределы:

Пример 4.f(x) = sign x = (лат. signum – знак). Функция задана на всей числовой оси (-∞, ∞), а область ее значений состоит из трех чисел: -1, 0, 1 (рис.5). Стрелки означают, что полупрямые не достигают точек на оси ординат, так как при x = 0 значение функции определено по другому соответствию: f(0) = 0. То есть 1-е условие непрерывности соблюдается.

Рис.5

2-е условие непрерывности нарушено – в самой точке x = 0 не существует 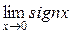, хотя функция имеет конечные левый и правый пределы:

Сама же точка x = 0 является точкой разрыва 1-го рода функции sign x, поскольку пределы слева и справа не равны друг другу.

3) Определение 4. Точка x = x₀ называется точкой разрыва 2-го рода функции f(x), если в этой точке функция не имеет, по крайней мере, одного из односторонних пределов или хотя бы один из них бесконечен (рис.6).

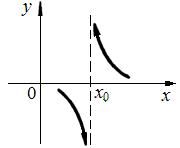
Рис.6

Пример 5. Для функции f(x) = 1/х точка x = 0 – точка разрыва 2-го рода, поскольку .

Пример 6. Для функции f(x) = sin(1/х) точка x = 0 – точка разрыва 2-го рода, так как ни левого, ни правого предела функции в этой точке не существует.

Итак, точка x = x₀ является точкой непрерывности функции у=f(x), если существуют конечные пределы справа и слева, и эти пределы равны значению функции в этой точке, т.е.

f(х₀ + 0) = f(х₀ – 0) = f(x₀).

Если эти равенства не выполняются или хотя бы один из односторонних пределов не существует, то точка x = x₀ – точка разрыва функции, причем:

1) если существуют односторонние пределы, но

f(х₀ + 0) = f(х₀ – 0) ≠ f(x₀) или f(x) в точке x₀ не определена, то x₀ – точка устранимого разрыва или

f(х₀ + 0) ≠ f(х₀ – 0) = f(x₀), то x₀ – точка разрыва 1-го рода.

2) если хотя бы один из пределов f(х₀ + 0) или f(х₀ – 0) не существует или бесконечен, то точка x₀ – точка разрыва 2-го рода.

Замечание 1. График непрерывной функции в точке рисуется при прохождении этой точки без отрыва ручки от листа бумаги.

Замечание 2. На языке (ε – δ) определение непрерывности повторяет определение предела, за исключением поведения функции в точке х₀.

Определение 5. Функция f(x) называется непрерывной в точке х₀, если для любого числа ε > 0 существует такое число δ(ε) > 0, что для всех х из промежутка |х – х₀| < δ выполняется неравенство |f(x) – f(x₀)| < ε.

В кванторах это определение выглядит так:

.

Для доказательства непрерывности функции f(x) в точке х₀ воспользуемся определением передела и 3-м условием непрерывности .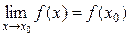

Обозначим х – х₀ = Δx. Тогда условие непрерывности можно переписать:

.

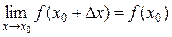По определению предела |f(x₀ + Δx) – f(x₀)| < ε.

Обозначим f(x₀ + Δx) – f(x₀) = α(х). Тогда |α(х)| < ε, а это означает, что α(х) есть бесконечно малая функция, т.е. .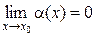

Следовательно, доказательством непрерывности функции f(x) в точке х₀ может служить равенство нулю предела

.

Отсюда сформулируем определение непрерывности на языке приращений.

Дадим значению аргумента х₀ произвольное приращение Δх = х – х₀. Тогда функция f(x) получит приращение Δу, определяемое как разность наращенного и исходного значений функции: Δу = f(х₀ + Δх) – f(x₀) = f(x) – f(x₀) (рис.7).

Рис.7

Определение 6. Функция f(x) – непрерывная в точке x = x₀, если она определена в этой точке, и бесконечно малому приращению аргумента Δх→0 соответствует бесконечно малое приращение функции Δу→0:

Определения 1 и 5 эквивалентны, поскольку фразы «если х → х₀, то f(x)→f(х₀)» и «если Δх = (x – x₀) → 0, то Δу = (f(x) – f(x₀)) → 0» равнозначны.

Определение 7. Функция f(x) – непрерывная на промежутке X, если она непрерывна в каждой точке этого промежутка.

Функция f(x) называется непрерывной на отрезке [а, b], если она непрерывна в каждой точке этого отрезка.

Теорема 1. Основные элементарные функции непрерывны в каждой точке своей области определения.

Поэтому можно считать, что для каждой основной элементарной функции ее область непрерывности совпадает с её областью определения D(f).

Пример 6. Показать, что функция у = х² непрерывна в любой точке х₀ числовой оси.

Решение: Составим разность f(х₀ + Δх) – f(x₀) = (х₀ + Δх)² – x₀² и и возьмем её предел при Δх → 0:

Значит, функция у = х² непрерывна в любой точке х₀.

Теорема 2. Все элементарные функции непрерывны в областях их определения.

Пример 7. Доказать непрерывность функции у = sin х на всей области определения.

Решение. Составим разность sin (х + Δх) – sin х,

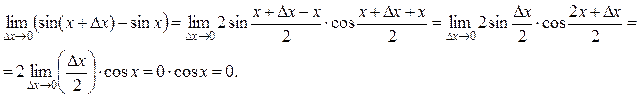
Это означает, что функция у = sin х непрерывна в любой точке х числовой оси.

Отсюда сформулируем правило: Если функция f(x) элементарна, и точка x₀ принадлежит области определения этой функции, то при вычислении предела функции при х → х₀ надо вместо х в выражение f(x) подставить х₀. Полученное число и является пределом функции f(x) в точке х = х₀:

Если f(x) – элементарна и х₀ є D(f), то .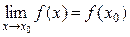

Замечание. Это правило верно лишь для элементарных функций. Непрерывность функции в любой точке области определения не гарантируется для неэлементарных функций. Так, функция у = [х], хотя и определена на всей числовой прямой, разрывна во всех целых точках. Другая неэлементарная функция – функция Дирихле, определенная на всей числовой прямой, имеет разрыв в каждой точке.