рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Механика
- /
- Теоретическая и прикладная механика
Реферат Курсовая Конспект
Теоретическая и прикладная механика
Теоретическая и прикладная механика - раздел Механика, Министерство Образования И Науки Российской Федерации Федеральное Го...
Министерство образования и науки Российской Федерации
Федеральное государственное автономное образовательное учреждение
высшего профессионального образования
«Российский государственный профессионально-педагогический университет»
Машиностроительный институт
Кафедра механики
Задания и методические указания
для выполнения контрольных работ
по дисциплине «Теоретическая и прикладная механика»
для студентов всех форм обучения специальности
050501.65 Профессиональное обучение (машиностроение и
технологическое оборудование)
специализаций 030503.19, 030504.19, 030510.19, 030503.09
и по дисциплине «Техническая механика»
для студентов всех форм обучения специальности
050501.65 Профессиональное обучение (машиностроение и
технологическое оборудование)
специализации 030501.15
Екатеринбург
Задания и методические указания для выполнения контрольных работ по дисциплине «Теоретическая и прикладная механика» и по дисциплине
«Техническая механика» (ГОС-2000). Екатеринбург: ФГАОУ ВПО «Рос. гос. проф.-пед. университет, 2012. - 67 с.
Составители: доц., канд. техн. наук Е. Д. Колегова;
доц., канд. техн. наук М.Ю. Туев;
доц., канд. техн. наук Н.Н.Эльяш
Одобрены на заседании кафедры механики. Протокол от 26 января 2012 г., № 5
Зав. кафедрой О.С. Лехов
Рекомендовано к печати методической комиссией Машиностроительного института РГППУ. Протокол от 15 февраля 2012 г., № 6
Председатель методической
комиссии МаИ РГППУ А.В. Песков
Ó ФГАОУ ВПО «Российский
государственный
профессионально –
педагогический
университет», 2012 Е. Д. Колегова, М.Ю. Туев, Н.Н.Эльяш

Введение
Механика – это область науки, цель которой – изучение движения и напряженного состояния элементов машин, строительных конструкций, сплошных сред и т. п. под действием приложенных к ним сил. Механику принято делить на теоретическую и прикладную. В теоретической механике устанавливаются общие закономерности изучаемых объектов вне связи с их конкретным практическим приложением. Под термином «прикладная механика» понимают область механики, посвященную изучению движения и напряженного состояния реальных технических объектов – конструкций, машин, робототехнических систем и т. п. – с учетом основных закономерностей, установленных в теоретической механике. Дисциплина «Техническая механика» имеет четко выраженную инженерную направленность, при которой классические положения механики изучаются в контексте профиля подготовки специалистов. Как «Теоретическая и прикладная механика», так и «Техническая механика» - это комплексные дисциплины, которые включают в себя в том или ином объеме основные положения курсов «Теоретическая механика», «Сопротивление материалов», «Теория механизмов и машин», «Детали машин». Учебная программа предусматривает изучение таких вопросов, как общие законы равновесия и движения материальных тел; основные методы расчета на прочность, жесткость и устойчивость отдельных деталей и узлов машин; устройство, область применения и основы проектирования деталей машин общего назначения.
Чтобы хорошо усвоить дисциплину, нужно не только глубоко изучить учебный материал, но и получить твердые навыки в решении задач. Для этого необходимо самостоятельно решить достаточно большое их количество по всем разделам курса из соответствующих сборников и выполнить ряд специальных заданий.
Задания к контрольным работам содержат 11 задач и состоят из двух частей. Первая часть заданий включает 6 задач, в том числе две задачи по разделу «Статика», две – по разделу «Кинематика» и две – по разделу «Динамика». Здесь же приведены примеры выполнения заданий.
Задачи по разделу «Сопротивление материалов» и примеры их выполнения содержатся во второй части.
В зависимости от специализации студента и от срока обучения ниже приведена таблица выполнения контрольных заданий по семестрам.
При изучении материала курса по учебнику нужно прежде всего уяснить суть каждого рассматриваемого в нем вопроса. Главное – это понять изложенное в учебнике, а отнюдь не заучить.
Осваивать учебный материал рекомендуется по главам (параграфам) учебника. Сначала следует прочитать весь материал темы, не задерживаясь особенно на фрагментах, которые показались не совсем понятными (часто ответы на возникающие вопросы можно найти в последующем материале). Затем надо вернуться к местам, вызвавшим затруднения, и внимательно разобраться в том, что было неясно. Особое внимание при повторном чтении необходимо обратить на формулировки соответствующих определений, теорем и т. п. (они обычно бывают набраны в учебнике курсивом или разрядкой); в точных формулировках, как правило, существенно каждое слово, и очень полезно понять, почему данное положение сформулировано именно так. Однако не требуется заучивать формулировки; важно понять их смысл.
Перед тем как приступить к решению задач надо сначала обязательно разобраться в решениях аналогичных задач, которые приводятся в учебнике, и при этом особое внимание обратить на методические рекомендации по их решению. Расчеты следует производить с помощью калькулятора. После нахождения искомых величин нужно проставить их размерность.
Для успешного выполнения контрольных работ необходимо знать следующие правила:
1. Нельзя приступать к выполнению контрольных работ, не изучив соответствующий раздел и не разобрав примеры решения каждой задачи. В этом случае при выполнении контрольных работ у студента возникнут затруднения.
2. Контрольные работы имеют индивидуальный характер: расчетные схемы и числовые данные для каждой задачи выбираются в соответствии с учебным шифром (тремя последними цифрами номера зачетной книжки студента). По цифрам шифра определяются строки, а позиции, которые занимают цифры в шифре, указывают столбцы в таблице с данными. Исходные данные для вариантов задачи находятся на пересечении соответствующих строк и столбцов.
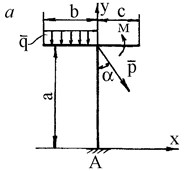
Например, учебному шифру 386 в табл. 1 (задача 1) соответствуют следующие данные: сила Р=15 кН, момент М=8 кН×м, интенсивность распределенной нагрузки q=6 кН/м, расстояния а=4 м, b=3 м, с=3 м, схема № 6 (рис. 1), угол α=30°, исследуемая реакция – МА.
3. Выбор контрольных заданий, выполняемых студентами, осуществляется по таблице в зависимости от специализации. Так, например, студенты специализации 030501.09 при сроке обучения 5 лет 4 месяца выполняют все задачи, отмеченные галочками; студенты специализации 030510.19, тоже обучающиеся 5 лет 4 месяца, выполняют задачи 1, 2, 8, 9.
4. Контрольные работы следует выполнять ручкой с синей или черной пастой четким почерком, рисунки – карандашом, с применением чертежного инструмента. Возможно оформление работ на компьютере. Необходимо оставлять поля 40 мм с левой стороны страницы для замечаний рецензента, а после решения каждой задачи – 1–2 чистые страницы для указаний рецензента. На обложке тетради должны быть четко написаны: название контрольной работы, дисциплины; фамилия, имя, отчество студента; наименование факультета и специальности; учебный шифр студента; дата отсылки работы; точный почтовый адрес.
| Специализация | Срок обучения | Семестры | Задачи | ||||||||||
| 030501.09 – Технология и технологический менеджмент в литейном производстве | 5 лет, 4 месяца | 4,4,5,5 | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ |
| 3,5 года | 3,3,4 | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | |
| 030503.19 Электротехника, электротехнологии и технологический менеджмент | 5 лет, 4 месяца | √ | √ | ─ | √ | ─ | √ | √ | √ | ─ | ─ | ─ | |
| 3,5 года | √ | √ | ─ | √ | ─ | √ | √ | √ | ─ | ─ | ─ | ||
| 030504.19 Электроэнергетика, энергоаудит, энергосбережение | 5 лет, 4 месяца | √ | √ | ─ | √ | ─ | √ | √ | √ | ─ | ─ | ─ | |
| 3,5 года | √ | √ | ─ | √ | ─ | √ | √ | √ | ─ | ─ | ─ | ||
| 030510.19 Профессионально-педагогические технологии | 5 лет, 4 месяца | 3,4 | √ | √ | ─ | √ | ─ | √ | √ | √ | √ | ─ | ─ |
| 3,5 года | √ | √ | ─ | ─ | ─ | ─ | ─ | √ | √ | ─ | ─ | ||
| 030501.15 Эксплуатация и ремонт автомобильного транспорта | 5 лет, 4 месяца | 4,5,5 | √ | √ | ─ | √ | √ | ─ | √ | √ | √ | √ | √ |
| 3,5 года | √ | √ | ─ | ─ | ─ | ─ | ─ | √ | √ | ─ | ─ |
Таблица выбора контрольных заданий в зависимости от специализации
5. Перед решением задачи необходимо указать номер задачи и записать, что в задаче дано и что требуется определить (текст задачи можно не переписывать). Далее следует выполнить эскиз с учетом условий решаемого варианта задачи: все углы, действующие силы, количество тел и их расположение на рисунке должны соответствовать данным условиям. Эскиз должен быть аккуратным и наглядным, его размеры должны быть такими, чтобы можно было ясно показать векторы всех сил, скоростей, ускорений и т. д., а также координатные оси.
6. Решение каждой задачи должно сопровождаться краткими пояснениями и четкими эскизами. Следует избегать многословных пояснений и пересказа учебника. Необходимо указывать размерность всех величин и подчеркивать окончательные результаты. Во всех случаях в числе целесообразно учитывать не более трех значащих цифр, так как излишняя точность ведет к непроизводительной трате времени.
7. Работы, выполненные с нарушением данных правил, не проверяются и не засчитываются.
8. При чтении текста каждой задачи следует учесть, что большинство рисунков дано без соблюдения масштаба. На рисунках к задачам все линии, параллельные строкам, считаются горизонтальными, а перпендикулярные строкам – вертикальными (это в тексте задач специально не оговаривается). Также без оговорок принято, что все нити (веревки, тросы) являются нерастяжимыми и невесомыми; нити, перекинутые через блок, по блоку не скользят; катки и колеса (в кинематике и динамике) катятся по плоскостям без скольжения. Все связи, если не сделано других оговорок, считаются идеальными. Когда тела на рисунке пронумерованы, то в тексте задач и в таблицах P1,  1, r1 и т. п. означают вес или размеры тела 1, а P2,
1, r1 и т. п. означают вес или размеры тела 1, а P2,  2, r2 – вес и размеры тела 2 и т. д.
2, r2 – вес и размеры тела 2 и т. д.
9. По получении из университета контрольной работы требуется исправить в ней все отмеченные ошибки и выполнить все указания преподавателя. Если работа не зачтена, следует в кратчайший срок исправить выявленные ошибки и представить ее вторично на проверку. Все исправления как в зачтенной, так и в незачтенной контрольной работе следует поместить в этой же тетради после рецензии преподавателя. Отдельно от работы исправления не рассматриваются.
10. При сдаче зачета и экзамена по курсу необходимо представлять зачтенные по данному разделу курса контрольные работы.
КОНТРОЛЬНАЯ РАБОТА ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ
Статика
1) изобразить тело, равновесие которого исследуется, на чертеже; 2) приложить к нему все активные (заданные) силы; 3) определить виды связей, наложенных на рассматриваемое тело, и, используя принцип освобождаемости от связей,…Пример решения задачи 1
Условие. Определить реакции опор для того способа закрепления бруса (рис. 2), при котором реакция – момент МА в заделке – имеет наименьшее значение.
Дано: Р = 5 кН, М = 10 кН×м, q = 2 кН/м, a = 60°, а = 4 м, b = 2 м, с = 1 м.
| 
| 
|
Рис. 2
Решение. Рассмотрим систему уравновешивающихся сил, приложенных к конструкции. Равномерно распределенную нагрузку интенсивностью  заменим равнодействующей:
заменим равнодействующей:
Q = q×в = 4 кН.
Выбираем оси координат, изображая их на чертеже (рис. 3).
Действие связей на конструкцию заменяем их реакциями (см. рис. 3):
в схеме а: RAx, RAy, MA; в схеме б: 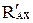 ,
, 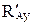 ,
, 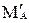 ; в схеме в:
; в схеме в: 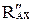 ,
,  ,
,  .
.

Рис. 3
Для решения задачи на равновесие тела, находящегося под действием плоской системы сил, используются в общем случае три уравнения равновесия. Для определения наименьшего значения момента МА найдем его величину для всех трех схем, не определяя пока остальных реакций, т. е. используем одно уравнение равновесия.
Силу Р разложим на две составляющие (Рx = Р×sin60°, Рy= P×cos60°) и найдем момент этой силы как сумму моментов ее составляющих.
Для схемы а
 ,
,
откуда
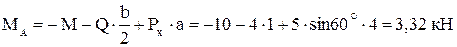 .
.
Для схемы б рациональнее составить уравнение равновесия относительно точки D – точки пересечения неизвестных реакций 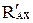 и RС:
и RС:

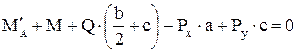 .
.
Вычисления дают
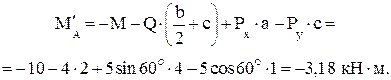
Для схемы в составим уравнение равновесия моментов относительно точки Е, где пересекаются линии действия неизвестных реакций RВ и 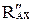 :
:

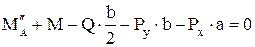 ,
,
откуда

Таким образом, наименьшее по модулю значение момента MA получается при закреплении бруса по схеме б. Определим остальные опорные реакции для этой схемы, используя для этого оставшиеся два уравнения равновесия:
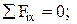
 , откуда
, откуда 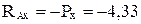 кН.
кН.
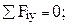
 , откуда
, откуда  кН.
кН.
Знак «минус» у найденной реакции 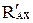 означает, что истинное направление этой реакции противоположно выбранному.
означает, что истинное направление этой реакции противоположно выбранному.
Проверим правильность решения задачи, для чего составим уравнение равновесия моментов относительно, например, точки К:

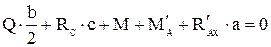 .
.
Подставим в это уравнение найденные значения  и
и 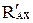 :
:
4×1+6,5×1+10 – 3,18 – 4,33×4 = 0.
Следовательно, задача решена верно.
Результаты расчета сводим в таблицу (табл. 2).
Таблица 2
| Схема (рис. 3) | Момент MA (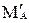 , ,  ), кН×м ), кН×м
| Силы, кН | |
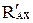
| RC | ||
| а | 3,32 | – | – |
| б | 3,18 | 4,33 | 6,50 |
| в | 16,32 | – | – |
Задача 2. Тема «Пространственная система сил»
Задача 2 – на равновесие твердого тела (вала), находящегося под действием системы сил, произвольно расположенных в пространстве. При решении данной задачи для определения искомых величин необходимо составить шесть уравнений равновесия [2, с. 86-89].
В случае, когда из общей схемы трудно определить момент силы относительно оси, рекомендуется изобразить на вспомогательной схеме проекцию рассматриваемого тела (вместе с силой) на плоскость, перпендикулярную данной оси. Если же при вычислении момента силы относительно оси возникают затруднения в определении проекции силы на соответствующую плоскость или плеча этой проекции, следует разложить силу на составляющие и воспользоваться теоремой Вариньона.
Исходные данные для различных вариантов приведены в табл. 3.
Условия:
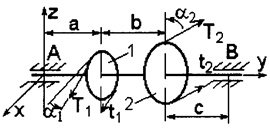
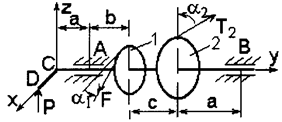
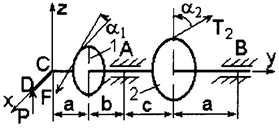
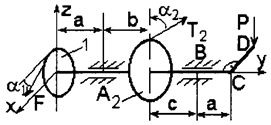
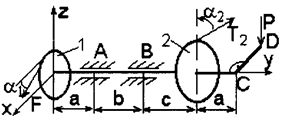
1. На горизонтальный вал, который может вращаться в подшипниках А и В, насажены шкив 1 радиусом r1 = 12 см и шкив 2 радиусом r2 = 16 см. Ветви ремней каждого шкива параллельны между собой и образуют соответственно углы α1 с горизонталью и α2 с вертикалью (рис. 4, схемы 1 – 3). Пренебрегая весом шкива и вала, найти натяжение ведущей и ведомой ветвей ремня, а также реакции подшипников при равновесии вала. Натяжение ведущей ветви ремня принять вдвое больше натяжения ведомой (T1 = 2t1; T2 = 2t2).
2. На горизонтальный вал насажены колесо 1 радиусом r1 = 20 см, колесо 2 радиусом r2 = 30 см и прикреплен перпендикулярно оси вала (параллельно оси х) рычаг СD длиной  = 20 см. К одному колесу приложена сила F, образующая с горизонталью угол α1, а к другому – сила Т2, образующая с вертикалью угол α2; к рычагу приложена вертикальная сила Р (рис. 4, схемы 4 – 7). Пренебрегая весом вала, колес и рычага, определить силу Р, при которой вал находится в равновесии, а также реакции подшипников А и В.
= 20 см. К одному колесу приложена сила F, образующая с горизонталью угол α1, а к другому – сила Т2, образующая с вертикалью угол α2; к рычагу приложена вертикальная сила Р (рис. 4, схемы 4 – 7). Пренебрегая весом вала, колес и рычага, определить силу Р, при которой вал находится в равновесии, а также реакции подшипников А и В.
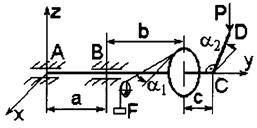
3. На горизонтальный вал насажено колесо радиусом r1 = 15 см и прикреплен перпендикулярно оси вала рычаг СD длиной  = 20 см, образующий с горизонтальной плоскостью угол α2. Веревка, намотанная на колесо и натягиваемая грузом F, сходит с колеса по касательной, наклоненной под углом α1 к горизонту (рис. 4, схемы 8 – 10). Пренебрегая весом вала, колеса и рычага и трением в блоке, определить вертикальную силу Р, при которой вал находится в равновесии, а также реакции подшипников А и В.
= 20 см, образующий с горизонтальной плоскостью угол α2. Веревка, намотанная на колесо и натягиваемая грузом F, сходит с колеса по касательной, наклоненной под углом α1 к горизонту (рис. 4, схемы 8 – 10). Пренебрегая весом вала, колеса и рычага и трением в блоке, определить вертикальную силу Р, при которой вал находится в равновесии, а также реакции подшипников А и В.
Таблица 3
| Цифра шифра | 1-я цифра шифра | 2-я цифра шифра | 3-я цифра шифра | ||||||
| Номер условия | Номер схемы (рис. 4) | Расстояния, м | Силы, Н | Углы, град. | |||||
| a | b | c | F | T2 | α1 | α2 | |||
| 1,0 | 1,1 | 1,0 | |||||||
| 1,2 | 1,3 | 1,2 | |||||||
| 1,4 | 1,5 | 1,4 | |||||||
| 1,6 | 1,7 | 1,6 | |||||||
| 1,8 | 1,9 | 1,8 | |||||||
| 1,0 | 1,1 | 1,0 | |||||||
| 1,2 | 1,3 | 1,2 | |||||||
| 1,4 | 1,5 | 1,4 | |||||||
| 1,6 | 1,7 | 1,6 | |||||||
| 1,8 | 1,0 | 1,6 |
| 
| ||

| 
| ||
| 
| ||
| 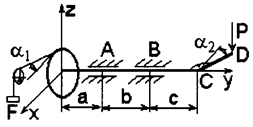
| ||

| 
|
Рис. 4. Схемы к задаче 2
Пример решения задачи 2
Условие. На горизонтальный вал насажено колесо радиусом r1 = 12 см и прикреплен перпендикулярно оси вала рычаг СD длиной  = 20 см, образующий с горизонтальной плоскостью угол α2=45°. Веревка, намотанная на колесо и натягиваемая грузом F=0,5 кН, сходит с колеса по касательной, наклоненной под углом α1=30° к горизонту. Пренебрегая весом вала, колеса, рычага и трением в блоке, определить вертикальную силу Р, при которой вал находится в равновесии, а также реакции подшипников А и В, если a = 1,8 м, b = 1,0 м, c = 1,6 м (см.рис. 4, схема 10).
= 20 см, образующий с горизонтальной плоскостью угол α2=45°. Веревка, намотанная на колесо и натягиваемая грузом F=0,5 кН, сходит с колеса по касательной, наклоненной под углом α1=30° к горизонту. Пренебрегая весом вала, колеса, рычага и трением в блоке, определить вертикальную силу Р, при которой вал находится в равновесии, а также реакции подшипников А и В, если a = 1,8 м, b = 1,0 м, c = 1,6 м (см.рис. 4, схема 10).
Решение. К валу кроме силы Р, действующей на рычаг СD, приложена реакция веревки (сила натяжения) T, численно равная силе тяжести груза F, так как, по условию задачи, трения в блоке нет (рис. 5, а). Направлена эта реакция вдоль веревки в ту сторону, куда веревка тянет блок. Реакции подшипников RA и RB, расположенные в плоскостях, перпендикулярных оси Аy, разложим на взаимно перпендикулярные составляющие RAx, RAz, RBx и RBz. Направление составляющих выбирается произвольно.
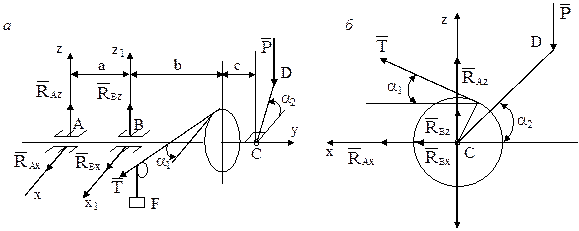
Рис. 5
Составим уравнения равновесия для вала, находящегося под действием произвольной пространственной системы сил, пять из которых – RAx, RAz, RBx, RBz и Р, – неизвестны по модулю. Для этого необходимо сделать вид с положительного направления координатных осей, например с оси Ay (рис. 5, б).
 (1)
(1)
 (2)
(2)
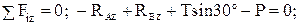 (3)
(3)
 (4)
(4)
 (5)
(5)
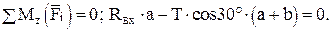 (6)
(6)
Из последнего соотношения найдем
 Н.
Н.
Из соотношения (5) определим

Из соотношения (4) вычислим
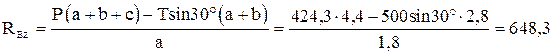 Н.
Н.
Из соотношения (3) найдем
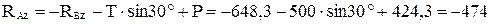 Н.
Н.
Из соотношения (1) выводим
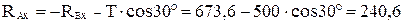 Н.
Н.
Знак «минус» перед значениями реакций RAz и RBx показывает, что эти реакции направлены противоположно указанным на рисунке.
Условие равновесия (2) обращается в тождество, так как проекции на ось y всех сил рассматриваемой системы равны нулю.
Для проверки правильности решения составим дополнительные контрольные уравнения равновесия моментов относительно осей x1 и z1 , проходящих через точку В:

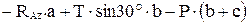 ;
;
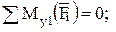
 .
.
Подставив значения найденных реакций в эти уравнения, получим:
474×1,8+500×0,5×1,0–424,3×2,6 = 0;
240,6×1,8–500×cos30°×1,0 = 0.
Контрольные уравнения обращаются в тождества, что свидетельствует о правильности полученных ответов.
Модули реакций подшипников:
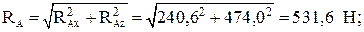

Результаты расчета сводим в таблицу (табл. 4).
Таблица 4
| Силы, Н | ||||||
| P | RAx | RAz | RA | RBx | RBz | RB |
| 240,6 | – 474 | 531,6 | – 673,6 | 648,3 | 934,9 |
Кинематика
Задача 3 посвящена определению скоростей и ускорений точек твердого тела при поступательном и вращательном движениях [1, 117-120,125-126]. Условие. Движение груза должно описываться уравнением x=C2t2+C1t+C0,Пример решения задачи 3
Условие. Найти уравнение движения груза, а также скорости и ускорения груза и точки М (рис. 7) в момент времени t = t1 , если R2 = 80 см, r2 = 50 см, R3 = 40 см, х0 = 6 см, v0 = 10 см/с, х2 = 256 см, t1 = 3 с, t2 = 5 с, r3 = R3 /2 = 20 см.
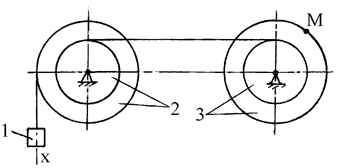
Рис. 7
Решение:
1. Уравнение движения груза 1 имеет вид
х = C2t2 + C1t + С0. (1)
Коэффициенты С0, С1 и С2 могут быть определены из следующих условий:
при t0 = 0 х0= 6 см,  0 = v0 = 10 см/с; (2)
0 = v0 = 10 см/с; (2)
при t2 = 5с х2 = 256 см. (3)
Скорость груза 1
v =  = 2 С2t + С1. (4)
= 2 С2t + С1. (4)
Подставляя (2) и (3) в выражения (1) и (4), находим коэффициенты
С0= 6 см, С1= 10 см/с, С2= 8 см/с2.
Таким образом, уравнение движения груза 1 имеет вид
x=8t2+10t+6. (5)
Скорость груза 1
v =  = 16t + 10. (6)
= 16t + 10. (6)
Ускорение груза 1
a = 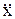 = 16 см / с2.
= 16 см / с2.
2. Для определения скорости и ускорения точки М запишем уравнения, связывающие скорость груза v и угловые скорости колес 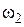 и
и 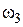 .
.
В соответствии со схемой механизма

откуда

или, с учетом (6) после подстановки данных,
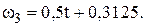
Угловое ускорение колеса 3
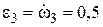 рад /с2.
рад /с2.
Скорость точки М, ее вращательное  , центростремительное
, центростремительное  и полное ам ускорения определяются по формулам
и полное ам ускорения определяются по формулам

 ;
;

 .
.
Результаты вычислений для заданного момента времени t1= 3 с приведены в табл. 6.
Таблица 6
| v, см / с | а, см /с2 |  , рад / с , рад / с
| 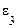 , рад / с2 , рад / с2
| vм, см /с |  , см /с2 , см /с2
|  , см /с2 , см /с2
|
| 1,81 | 0,5 | 72,5 | 20,0 | 131,4 |
Скорости и ускорения тела 1 и точки М показаны на рис. 8.
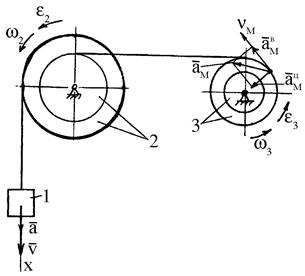
Рис. 8
Задача 4. Тема «Плоское движение твердого тела»
Поскольку задача 4 относится к теме «Плоское движение твердого тела» [1, 127-130, 132], скорость ползуна для данного положения механизма можно вычислить с помощью мгновенного центра скоростей шатуна. Для этого необходимо знать скорость какой-нибудь точки шатуна (например точки А) и направление скорости ползуна.
Ускорение ползуна в данный момент времени можно найти с помощью векторной формулы распределения ускорений точек плоской фигуры, спроектировав ее на два взаимно перпендикулярных направления. В качестве полюса удобно принять точку А.
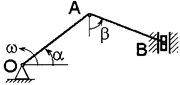
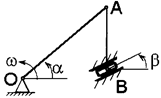
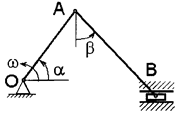
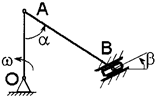
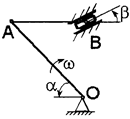
Условие. Кривошип ОА длиной R вращается вокруг неподвижной оси О с постоянной угловой скоростью w и приводит в движение шатун АВ длиной  и ползун В. Для заданного положения механизма найти скорости и ускорения ползуна В и точки С, а также угловую скорость и угловое ускорение звена, которому эта точка принадлежит.
и ползун В. Для заданного положения механизма найти скорости и ускорения ползуна В и точки С, а также угловую скорость и угловое ускорение звена, которому эта точка принадлежит.
Схемы механизмов приведены на рис. 9, а необходимые для расчета данные – в табл. 7.

| 
| ||
| 
| ||
| 
| ||

| 
| ||

| 
|
Рис. 9. Схемы к задаче 4
Таблица 7
| Цифра шифра | 1-я цифра шифра | 2-я цифра шифра | 3-я цифра шифра | ||||
| R, см |  , cм , cм
| a, град | b, град | w, c-1 | Номер схемы (рис. 9) | АС | |
| 0,2 (АВ) | |||||||
| 0,3 (АВ) | |||||||
| 0,4 (АВ) | |||||||
| 0,5 (АВ) | |||||||
| 0,6 (АВ) | |||||||
| 0,7 (АВ) | |||||||
| 0,6 (АВ) | |||||||
| 0,5 (АВ) | |||||||
| 0,4 (АВ) | |||||||
| 0,3 (АВ) |
Примечание. Если при заданных значениях углов окажется, что шатун АВ перпендикулярен направляющим ползуна (см. рис. 9, схемы 1, 6), то значение угла b следует принять равным 15°.
Пример решения задачи 4
Условие. Кривошип ОА длиной R=64 см вращается вокруг неподвижной оси О с постоянной угловой скоростью w=1 рад /с и приводит в движение шатун АВ длиной 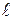 =80 см и ползун В. Для положения механизма, заданного значениями углов a=60°, b=45,° найти скорости и ускорения ползуна В и точки С, а также угловое ускорение звена, которому эта точка принадлежит (АС=0,5 АВ). Схема механизма приведена на рис. 10, а.
=80 см и ползун В. Для положения механизма, заданного значениями углов a=60°, b=45,° найти скорости и ускорения ползуна В и точки С, а также угловое ускорение звена, которому эта точка принадлежит (АС=0,5 АВ). Схема механизма приведена на рис. 10, а.
Решение:
1. Определим скорость точки А кривошипа как вращательную вокруг неподвижной точки О по соотношению  . Скорость точки А перпендикулярна кривошипу ОА. Для определения скорости точки В найдем положение мгновенного центра скоростейРАВ шатуна АВ, для чего покажем направление скоростей точек А и В (скорость ползуна В имеет вектор по направляющим n – n), а затем из точек А и В восстановим перпендикуляры к скоростям vA и vB. Мгновенный центр скоростей РАВ шатуна АВ находится на пересечении этих перпендикуляров (рис. 10, б).
. Скорость точки А перпендикулярна кривошипу ОА. Для определения скорости точки В найдем положение мгновенного центра скоростейРАВ шатуна АВ, для чего покажем направление скоростей точек А и В (скорость ползуна В имеет вектор по направляющим n – n), а затем из точек А и В восстановим перпендикуляры к скоростям vA и vB. Мгновенный центр скоростей РАВ шатуна АВ находится на пересечении этих перпендикуляров (рис. 10, б).

Рис. 10
Рассмотрим движение шатуна в данный момент времени как вращательное относительно оси, проходящей через мгновенный центр скоростей РАВ перпендикулярно неподвижной плоскости, по отношению к которой происходит плоское движение. Угловая скорость шатуна АВ в этом случае определяется из соотношения
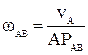 .
.
Модули скоростей точек В и С как вращательные – из соотношений 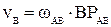 ;
;
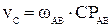 .
.
Расстояния АРАВ, BPАВ и СРАВ определим путем рассмотрения треугольников АВРАВ и АСРАВ, применив теоремы синусов и косинусов. Для заданного положения механизма получим
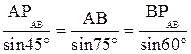 ,
,
откуда


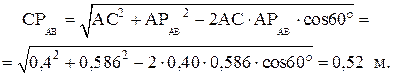
Подставив найденные значения расстояний в соответствующие формулы, получим
 ;
;
 ;
;
 .
.
Вектор  направлен перпендикулярно отрезку СРAB в сторону, соответствующую направлению вращения звена АВ.
направлен перпендикулярно отрезку СРAB в сторону, соответствующую направлению вращения звена АВ.
Направления скоростей показаны на рис. 10, б.
2. Для определения ускорений точек B, С и углового ускорения звена АВ воспользуемся векторным равенством, выбрав за полюс точку А, ускорение которой известно по величине и направлению:
 , (1)
, (1)
где  – ускорение ползуна В;
– ускорение ползуна В;  – ускорение точки А, выбранной за полюс;
– ускорение точки А, выбранной за полюс;  – центростремительное (осестремительное, нормальное) ускорение точки В при ее вращении вокруг полюса А;
– центростремительное (осестремительное, нормальное) ускорение точки В при ее вращении вокруг полюса А;  – вращательное (касательное) ускорение точки В при ее вращении вокруг полюса А.
– вращательное (касательное) ускорение точки В при ее вращении вокруг полюса А.
Ускорение точки А кривошипа в общем случае складывается из центростремительной  и вращательной составляющих
и вращательной составляющих  . Поскольку по условию кривошип ОА вращается равномерно, то
. Поскольку по условию кривошип ОА вращается равномерно, то  и ускорение точки А состоит только из центростремительной составляющей, модуль которой определяется по формуле
и ускорение точки А состоит только из центростремительной составляющей, модуль которой определяется по формуле
 .
.
Вектор ускорения точки А направлен к центру вращения звена О (рис. 10, в).
Центростремительное ускорение точки В определяется по формуле
 .
.
Вектор  направлен от точки В к полюсу – точке А.
направлен от точки В к полюсу – точке А.
Что касается ускорения точки В –  и вращательного ускорения
и вращательного ускорения  , то известны только линии действия этих векторов:
, то известны только линии действия этих векторов:  – по направляющей, расположенной под углом b к звену АВ;
– по направляющей, расположенной под углом b к звену АВ;  – перпендикулярно звену АВ.
– перпендикулярно звену АВ.
Зададимся произвольно их направлениями по указанным линиям (см. рис. 10, в) и спроектируем уравнение (1) на оси координат. Знак в ответе покажет, соответствует ли истинное направление вектора принятому при расчете.
Выбрав направления осей х и у, как показано на рис. 10, в, получаем
 ; (2)
; (2)
 . (3)
. (3)
Из уравнения (2) находим
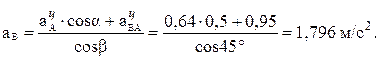
Направление ускорения  показано на рис. 10, в.
показано на рис. 10, в.
Из уравнения (3) получаем
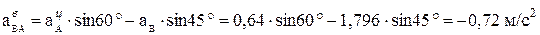 .
.
Знак «минус» показывает, что истинное направление  противоположно показанному на рис. 10, в.
противоположно показанному на рис. 10, в.
Ускорение  и все его составляющие с учетом их истинных направлений представлены на рис. 10, г.
и все его составляющие с учетом их истинных направлений представлены на рис. 10, г.
Угловое ускорение шатуна АВ с учетом того, что здесь  – алгебраическая величина, определяется по формуле
– алгебраическая величина, определяется по формуле
 .
.
Вычисляя, находим
 .
.
Направление ускорения  относительно полюса А определяет направление углового ускорения
относительно полюса А определяет направление углового ускорения 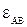 . Здесь под направлением углового ускорения понимается направление дуговой стрелки, которое при ускоренном вращении звена совпадает с направлением его вращения, а при замедленном – противоположно ему. В данном случае угловое ускорение совпадает с направлением вращения шатуна.
. Здесь под направлением углового ускорения понимается направление дуговой стрелки, которое при ускоренном вращении звена совпадает с направлением его вращения, а при замедленном – противоположно ему. В данном случае угловое ускорение совпадает с направлением вращения шатуна.
3. Для определения ускорения точки С воспользуемся векторным уравнением
 . (4)
. (4)
Вращательное и центростремительное ускорения точки С во вращательном движении звена АВ вокруг полюса А определяются следующим образом:
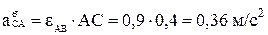 ;
;
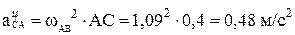 .
.
Вектор 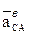 перпендикулярен вектору
перпендикулярен вектору 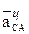 и направлен соответственно угловому ускорению
и направлен соответственно угловому ускорению 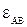 (см. рис. 10, в).
(см. рис. 10, в).
Ускорение точки С находим, проектируя уравнение (4) на оси координат (см. рис. 10, в):
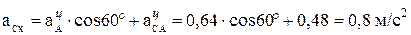 ;
;
 .
.
Полное ускорение точки С

Динамика
Задача 5 является прямой задачей динамики точки: по известным (заданным) силам и начальным условиям движения требуется определить движение точки,… Условия: 1. Тяжелая материальная точка М брошена под углом a к горизонту со скоростью v0. В начальный момент времени точка…Пример решения задачи 5
Условие. Груз весом Р движется вверх по шероховатой наклонной плоскости, составляющей угол a = 30°с горизонтом. Коэффициент трения скольжения груза о плоскость f = 0,1. В начальный момент груз находился в положении М0 на расстоянии a = 8 м от начала координат и имел скорость v0=25 м/с. Определить уравнение движения груза в заданной системе координат (рис. 12).

Рис. 12
Решение:
1. Пусть тело в произвольный момент времени t занимает положение М на наклонной плоскости. Освободим тело от связи (наклонной плоскости), заменив ее действие нормальной составляющей реакции N и силой трения Fтр. Таким образом, к телу приложена система трех сил Р, N, Fтр, под действием которых совершается движение по шероховатой наклонной плоскости.
2. Примем тело за материальную точку. Проектируя основное уравнение динамики точки

на оси декартовых координат Оx и Оy (ось Оx совпадает с направлением движения точки), получим два дифференциальных уравнения:
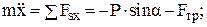 (1)
(1)
 (2)
(2)
Здесь m – масса точки;  – проекции ускорения точки на соответствующие оси.
– проекции ускорения точки на соответствующие оси.
Так как тело движется прямолинейно вдоль оси Оx, то проекция ускорения на ось Оy равна нулю. Следовательно, уравнение (2) примет вид
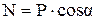 . (3)
. (3)
По закону Кулона, сила трения определяется выражением
Fтр = f × N
или, с учетом (3),
Fтр=f·P·cosa.
Подставляя выражение для Fтр в уравнение (1), получим
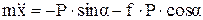 .
.
Поскольку
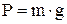 ,
,
где 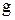 – ускорение свободного падения тела (g=9,81 м/с2), то после очевидных преобразований получим следующее дифференциальное уравнение второго порядка:
– ускорение свободного падения тела (g=9,81 м/с2), то после очевидных преобразований получим следующее дифференциальное уравнение второго порядка:
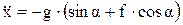 .
.
Для понижения порядка уравнения произведем замену

(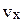 – проекция скорости тела на ось Ох), получим дифференциальное уравнение первого порядка с разделяющимися переменными:
– проекция скорости тела на ось Ох), получим дифференциальное уравнение первого порядка с разделяющимися переменными:
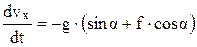 .
.
Разделив переменные, проинтегрируем дифференциальное уравнение с учетом того, что при t=0 vx=v0 = 25 м/с:

 (4)
(4)
Проинтегрируем дифференциальное уравнение (4) еще раз, сделав замену  и учитывая, что при t=0 x=x0=a:
и учитывая, что при t=0 x=x0=a:

 (5)
(5)
Подставив в полученное выражение (4) значения заданных величин, окончательно получим следующее уравнение движения груза:

Задача 6. Тема «Применение теоремы об изменении
кинетической энергии»
Данная задача посвящена исследованию движения механической системы с помощью теоремы об изменении кинетической энергии в интегральной форме. Решение подобных задач рекомендуется осуществлять в такой последовательности:
1) изобразить систему в произвольный момент времени; показать на чертеже все действующие на систему силы (заданные и реакции связей);
2) записать теорему об изменении кинетической энергии механической системы в интегральной форме;
3) подсчитать кинетическую энергию системы в начальном и конечном положениях, выразив ее через скорость звена, движение которого требуется определить (или задано);
4) подсчитать сумму работ внешних и внутренних сил на искомых (или заданных) перемещениях точек системы, выразив их через перемещение того звена, движение которого определяется (или задано);
5) подставить полученные значения кинетической энергии и работ в формулу теоремы и найти искомую величину.
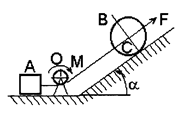
Условие. Однородный каток В весом Q и радиусом R соединен гибкой невесомой и нерастяжимой нитью с грузом А весом Р (рис. 13). Нить переброшена через невесомый блок О радиусом r. К оси С катка (см. рис. 13, схемы 1 – 5), или к грузу А (см. рис. 13, схемы 6 – 8), или к свободному концу нити (см. рис. 13, схемы 9,10) приложена сила F, линейно зависящая от величины перемещения S.

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
|
Рис. 13. Схемы к задаче 6
Каток катится без проскальзывания; коэффициент трения скольжения груза о плоскость равен f, момент сил сопротивления в подшипнике блока – М. Определить скорость груза А, когда он переместится на величину S. В начальный момент система находилась в покое.
Исходные данные для решения задачи приведены в табл. 9.
Таблица 9
| Цифра шифра | 1-я цифра шифра | 2-я цифра шифра | 3-я цифра шифра | ||||||
| r, см | S, м | M, Н м | Силы, кН | Номер схемы (рис. 13) | a, град | f | |||
| P | Q | F | |||||||
| 2,1 | 1,1 | 3,1 | 8,1+0,5S | 0,06 | |||||
| 2,2 | 1,2 | 3,2 | 8,2+0,4S | 0,07 | |||||
| 2,3 | 1,3 | 3,3 | 8,3+0,3S | 0,08 | |||||
| 2,4 | 1,4 | 3,4 | 8,4+0,2S | 0,09 | |||||
| 2,5 | 1,5 | 3,5 | 8,5+0,1S | 0,10 | |||||
| 2,6 | 1,6 | 3,6 | 8,6+0,5S | 0,06 | |||||
| 2,7 | 1,7 | 3,7 | 8,7+0,4S | 0,07 | |||||
| 2,8 | 1,8 | 3,8 | 8,8+0,3S | 0,08 | |||||
| 2,9 | 1,9 | 3,9 | 8,9+0,2S | 0,09 | |||||
| 3,0 | 2,0 | 4,0 | 9,0+0,1S | 0,10 |
Пример решения задачи 6
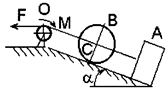
Условие. Однородный каток В весом Q=3,5 кН и радиусом R помещен на гладкую плоскость, составляющую с горизонтом угол a=300, соединен гибкой невесомой и нерастяжимой нитью с грузом А, вес которого Р=1,5 кН (рис. 14). Груз А перемещается по шероховатой плоскости, наклоненной к горизонту под углом a=300. Нить переброшена через невесомый блок О радиусом r=20 см. К оси с катка В приложена сила F, линейно зависящая от величины перемещения s: F=8,5+0,2×s (кН). Каток катится без скольжения; коэффициент трения скольжения груза о плоскость f=0,1, момент сил сопротивления в подшипнике блока М=200 Н×м. Определить скорость груза А, когда он переместится на величину s=2,5 м. В начальный момент система находилась в покое.
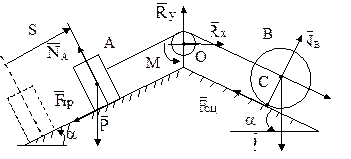
Рис. 14
Решение:
1. Изобразим механическую систему, состоящую из катка В, блока О, груза А и нити, в промежуточный момент времени. Система действующих на нее сил включает активные силы Q, P, F, момент трения М в блоке О и реакции связей NA, NB, Fсц, Fтр, Rx, Ry.
2. Запишем формулу, выражающую теорему об изменении кинетической энергии механической системы в конечной (интегральной) форме:
 (1)
(1)
где T1, T0 – кинетическая энергия механической системы соответственно в конечный и начальный моменты времени; 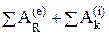 – суммы работ соответственно всех внешних и внутренних сил, действующих в данной системе.
– суммы работ соответственно всех внешних и внутренних сил, действующих в данной системе.
Рассматриваемая механическая система состоит из абсолютно твердых тел, соединенных идеальной нитью. Для таких систем с идеальными связями сумма работ всех внутренних сил равна нулю, т. е.
 (2)
(2)
3. Найдем кинетическую энергию механической системы в начальном и конечном положениях.
По условию задачи система в начальный момент времени находилась в покое; следовательно, ее кинетическая энергия в этот момент равна нулю (T0=0).
Кинетическую энергию груза А, движущегося поступательно, вычислим как
 ,
,
где 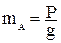 – масса груза А;
– масса груза А;  – скорость груза.
– скорость груза.
Кинетическая энергия катка В, совершающего плоское движение, определяется как
 ,
,
где  – масса катка В; vC – скорость центра масс С катка,
– масса катка В; vC – скорость центра масс С катка, 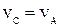 ;
;  – момент инерции катка относительно оси z, проходящей через его центр масс; wВ – угловая скорость катка,
– момент инерции катка относительно оси z, проходящей через его центр масс; wВ – угловая скорость катка,  .
.
Кинетическая энергия системы равна сумме кинетических энергий всех тел, входящих в нее:
 (3)
(3)
4. Найдем сумму работ всех внешних сил системы на соответствующих перемещениях точек их приложения:
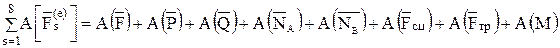 .
.
Работы сил  и
и 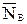 равны нулю, так как направления этих сил составляют прямой угол с направлениями перемещений точек их приложения.
равны нулю, так как направления этих сил составляют прямой угол с направлениями перемещений точек их приложения.
Работа силы сцепления Fсц равна нулю, поскольку приложена к точке катка, совпадающей в данный момент времени с мгновенным центром скоростей (каток движется без проскальзывания).
Работы реакций Rx и Rу равны нулю, так как эти силы приложены к неподвижным точкам. Работы сил F, Р, Q, Fтр и пары сил с моментом М определим следующим образом:
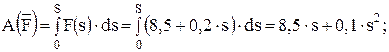

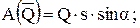
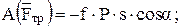
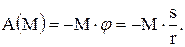
После суммирования получим
 . (4)
. (4)
Подставляя выражения (2) – (4) в формулу (1), получим
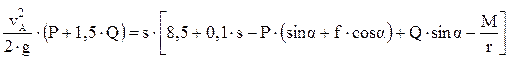 .
.
Отсюда искомая скорость груза А, в момент, когда он переместится на расстояние 2,5 м, определяется как
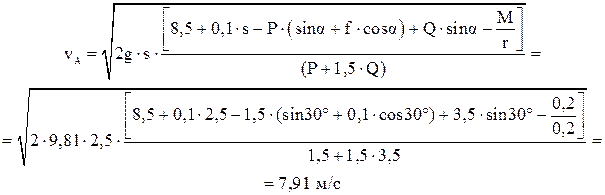
КОНТРОЛЬНАЯ РАБОТА ПО СОПРОТИВЛЕНИЮ МАТЕРИАЛОВ
Условие. Произвести расчет стержня постоянного сечения (рис. 1) на прочность и жесткость. Материал стержня – сталь с допускаемым напряжением… 1) вычислить продольные силы на участках стержня и построить эпюру продольных… 2) определить размеры поперечного сечения (сторону квадрата или диаметр);Пример решения задачи 7
Условие. Произвести расчет цилиндрического стержня переменного поперечного сечения (рис. 2, в) на прочность и жесткость. Материал стержня – сталь с допускаемым напряжением [σс] = [σр] = 210 МПа и модулем Юнга Е = 2,1·105 МПа. На стержень действуют силы F1 = 500 кН; F2 = 900 кН; F3 = 1500 кН; размеры участков: 1 = 0,6 м;
1 = 0,6 м;  2 = 0,4 м;
2 = 0,4 м;  3 = 1,0 м. Построить эпюры продольных сил N, нормальных напряжений σ и продольных перемещений δ. Определить диаметр стержня, исходя из условия равнопрочности всех его участков.
3 = 1,0 м. Построить эпюры продольных сил N, нормальных напряжений σ и продольных перемещений δ. Определить диаметр стержня, исходя из условия равнопрочности всех его участков.
Решение. Составим уравнение равновесия сил на ось у:
Σ Fy = 0;
Σ Fy = – RАy + F1 – F2 + F3 = 0,
откуда
RАy = F1 – F2 + F3 = 500 – 900 + 1500 = 1100 кН.
Для определения внутренней продольной силы в различных сечениях выделим участки нагружения стержня. Сечения, разделяющие намеченные три участка, проходят через точки приложения сил и перпендикулярны оси их приложения.
Разрежем мысленно стержень по сечениям I – I, II – II, III – III. Из условия равновесия стержня ниже сечения I – I получим, что внутренняя продольная сила NI ‑ I = F1 = 500 кН (растяжение).
Из условия равновесия стержня ниже сечений II – II и III – III получим
NII ‑ II = F1 – F2 = 500 – 900 = – 400 кН;
NIII – III = F1 – F2 + F3 = 500 – 900 + 1500 = 1100 кН.
Отрицательное значение NII – II свидетельствует о деформации сжатия на этом участке, положительное значение NIII – III – о растяжении.
Выбрав масштаб, построим эпюру продольных сил (рис. 2, б). При этом растягивающую силу считаем положительной, а сжимающую – отрицательной.
Из условия равнопрочности всех участков стержня определим площади и диаметры поперечных сечений.
На участке между сечениями А – А и В – В
А1 = N1 / [σр] = 5 · 105 / 210 · 106 = 2,4 · 10–3 м2,
откуда диаметр стержня
d1 = 0,055 м.
На участке между сечениями В – В и С – С
А2 = N2 / [σс] = 4 · 105 / 210 · 106 = 1,9 ·10–3 м2,
откуда диаметр стержня
d2 = 0,049 м.
На участке между сечениями С – С и D – D
А3= N3 / [σр] = 1,1 · 106 / 210 · 106 = 5,2 · 10–3 м2,
откуда диаметр стержня
d3= 0,082 м.
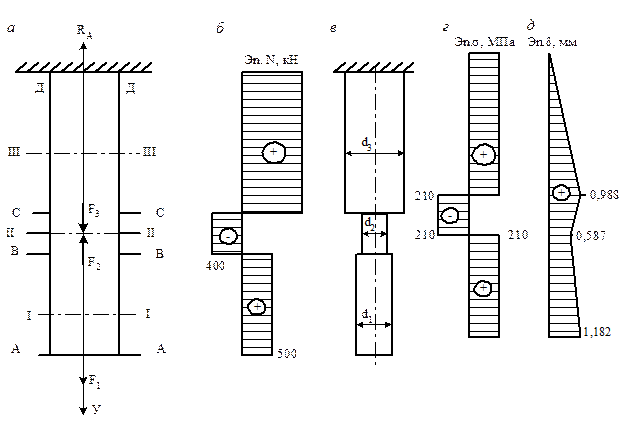
Рис. 2
Для вычисления перемещений определим деформации каждого из трех участков. Для этого преобразуем зависимость, выражающую закон Гука:
ε = σ/Ε,
где ε = Δ /
/  0 = (
0 = ( 1 –
1 –  0) /
0) /  0 – относительное удлинение стержня; Δ
0 – относительное удлинение стержня; Δ – абсолютное удлинение стержня;
– абсолютное удлинение стержня;  0 – длина стержня до деформации;
0 – длина стержня до деформации;  1 – длина стержня после деформации; σ = N / A – напряжение; Е – модуль Юнга.
1 – длина стержня после деформации; σ = N / A – напряжение; Е – модуль Юнга.
Подставив значения ε и σ, получим
Δ /
/  0 = N / ЕA,
0 = N / ЕA,
откуда
Δ = N ·
= N ·  0 / ЕA.
0 / ЕA.
Деформацию соответствующих участков находим как
Δ 1 = N1
1 = N1  01 / ЕA1 = 5·105 · 0,6 / 2,1 · 105 · 106·2,4 · 10–3 =5,95·10–4 м =0,595 мм;
01 / ЕA1 = 5·105 · 0,6 / 2,1 · 105 · 106·2,4 · 10–3 =5,95·10–4 м =0,595 мм;
Δ 2 = N2
2 = N2 02/ ЕA2= 4 · 105· 0,4 / 2,1 · 105 · 106 · 1,9 · 10–3 = – 4,01 · 10–4 м = – 0,401 мм;
02/ ЕA2= 4 · 105· 0,4 / 2,1 · 105 · 106 · 1,9 · 10–3 = – 4,01 · 10–4 м = – 0,401 мм;
Δ 3= N3
3= N3 03/ ЕA1 = 1,1·106·1 / 2,1·105·106·5,3·10–3 = 9,88·10 –4 м =0,988 мм.
03/ ЕA1 = 1,1·106·1 / 2,1·105·106·5,3·10–3 = 9,88·10 –4 м =0,988 мм.
Перемещение любого сечения стержня равно сумме деформаций участков, расположенных между сечением и опорой.
Перемещение сечения
D – D δD – D = 0.
Перемещение сечения С – С обусловлено деформацией участков, расположенных между D – D и C – C:
δС – С = Δ  3 = 0,988 мм.
3 = 0,988 мм.
Перемещение сечения В – В обусловлено деформацией двух участков, расположенных между D – D и C – C, а также между С – С и В – В.
Тогда
δВ – В = Δ  3 + Δ
3 + Δ  2 = 0,988 – 0,401 = 0,587 мм.
2 = 0,988 – 0,401 = 0,587 мм.
Из аналогичных рассуждений определим перемещение сечения А – А:
δА – А = Δ  3 + Δ
3 + Δ  2 + Δ
2 + Δ  1 = 1,182 мм.
1 = 1,182 мм.
В выбранном масштабе откладываем на эпюре (рис. 2, д) значения δС – С, δВ – В и δА – А и соединяем полученные точки прямыми линиями, так как при действии сосредоточенных внешних сил перемещения линейно зависят от абсциссы сечения. В результате получаем эпюру перемещений δ.
Задача 8. Тема «Кручение»
Условие. К стальному ступенчатому валу, имеющему сплошное цилиндрическое поперечное сечение, приложены четыре крутящих момента (рис. 3). Левый конец вала жестко закреплен в опоре, а правый – свободен. Требуется:
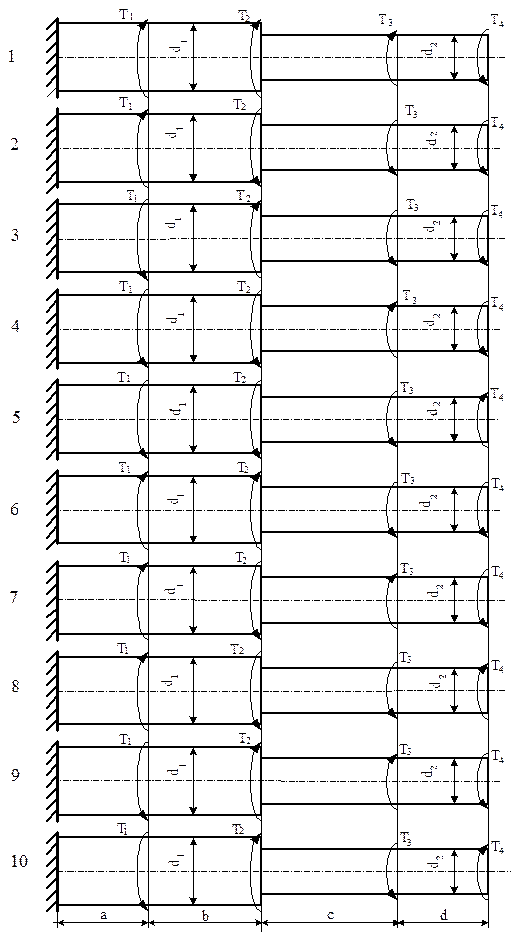
Рис. 3. Схемы валов к задаче 8
1) построить эпюру крутящих моментов Tк по длине вала;
2) при заданном значении допускаемого напряжения на кручение [τк] определить диаметры d1 и d2 вала из расчета на прочность (полученные результаты округлить).
Исходные цифровые данные приведены в табл. 2.
Таблица 2
| Цифра шифра | 1-я цифра шифра | 2-я цифра шифра | 3-я цифра шифра | ||||||
| Крутящие моменты, кНм | Расстояния, м | [τк], МПа | Номер схемы (рис. 3) | ||||||
| Т1 | Т2 | Т3 | Т4 | a | b | c | |||
| 5,1 | 2,1 | 1,1 | 0,1 | 1,0 | 1,0 | 1,0 | |||
| 5,2 | 2,2 | 1,2 | 0,2 | 1,1 | 1,1 | 1,1 | |||
| 5,3 | 2,3 | 1,3 | 0,3 | 1,2 | 1,2 | 1,2 | |||
| 5,4 | 2,4 | 1,4 | 0,4 | 1,3 | 1,3 | 1,3 | |||
| 5,5 | 2,5 | 1,5 | 0,5 | 1,4 | 1,4 | 1,4 | |||
| 5,6 | 2,6 | 1,6 | 0,6 | 1,5 | 1,5 | 1,5 | |||
| 5,7 | 2,7 | 1,7 | 0,7 | 1,6 | 1,6 | 1,6 | |||
| 5,8 | 2,8 | 1,8 | 0,8 | 1,7 | 1,7 | 1,7 | |||
| 5,9 | 2,9 | 1,9 | 0,9 | 1,8 | 1,8 | 1,8 | |||
| 6,0 | 3,0 | 2,0 | 1,0 | 1,9 | 1,9 | 1,9 |
Пример решения задачи 8
Условие. Рассмотрим решение задачи № 8 по варианту, соответствующему шифру зачетной книжки 000. По табл. 2 принимаем: схему 10; Т1 = 6,0 кНм; Т2 = 3,0 кНм; Т3 = 2,0 кНм; Т4 = 1,0 кНм; а = 1,9 м; b = 1,9 м; с = 1,9 м; [τ] = 50 МПа.
Решение. Для построения эпюры крутящих моментов разобьем вал на участки, границами которых являются характерные сечения (характерные сечения – сечения, в которых приложены внешние крутящие моменты, а также сечения, в которых изменяются поперечные размеры сечения вала).
Примем следующее правило знаков для внутреннего крутящего момента. Внутренний крутящий момент в сечении считается положительным, когда внешний момент вращает отсеченную часть вала против часовой стрелки (при взгляде на отсеченную часть со стороны сечения). Если же внешний момент вращает отсеченную часть по часовой стрелке (при взгляде со стороны сечения), то крутящий момент в сечении будем считать отрицательным.
Величина крутящего момента в данном сечении равна алгебраической сумме внешних вращающих моментов, приложенных к отсеченной части.
Используя метод сечений, определим значения внутренних крутящих моментов на участках вала, разделенных характерными сечениями.
I участок:
ТкI = Т4 = 1,0 кНм;
II участок:
ТкII = Т4 – Т3 = 1,0–2,0 = – 1,0 кНм;
III участок:
ТкIII = Т4 – Т3 + Т2 = 1,0–2,0 + 3,0 = 2,0 кНм;
IV участок:
ТкIV = Т4 – Т3 + Т2 – Т1 = 1,0–2,0 + 3,0 = 2,0 кНм.
Построим эпюру внутренних крутящих моментов Тк (рис. 4).
Определим из условия прочности при кручении диаметры вала:
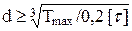 .
.
По условию задачи диаметры вала на участках I и II равны. Из анализа эпюры Тк видно, что крутящие моменты, действующие на этих участках, равны по абсолютной величине. Поэтому Тmax = 1 кНм. Тогда
 .
.
Полученное значение диаметра округляем до ближайшего (в сторону увеличения) из ряда диаметров по ГОСТ 6963–69. Принимаем d1= d2=48 мм.
Диаметры вала на участках III и IV по условию задачи одинаковы; Тmax = 4,0 кНм.
Тогда, поскольку на четвертом участке действует момент больший, чем на третьем,
 .
.
Принимаем d1 = 75 мм.

Рис. 4
Задача 9. Тема «Поперечный изгиб»
Условие. Для заданной схемы балки (рис. 5) требуется:
1) записать уравнение в общем виде для определения поперечных сил Q и изгибающих моментов Ми на каждом участке балки;
2) построить эпюры поперечных сил Q и изгибающего момента Mи;
3) найти максимальный изгибающий момент Мmax и подобрать по ГОСТу стальную балку двутаврового поперечного сечения.

| 
|
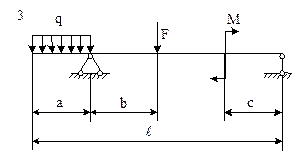
| 
|
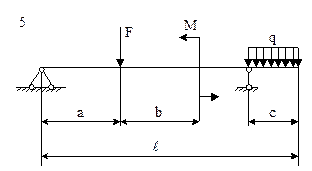
| 
|
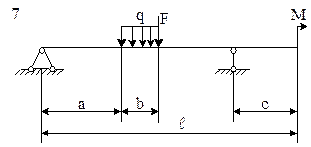
| 
|
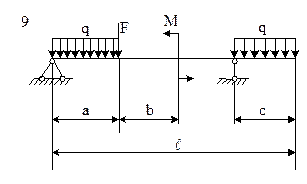
| 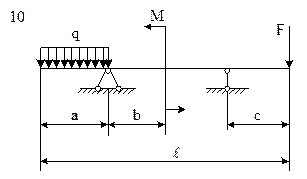
|
Рис. 5. Схемы к задаче 9
Допускаемое напряжение на изгиб принять равным [σи]=150 МПа.
Исходные цифровые данные представлены в табл. 3.
Таблица 3
| Цифра шифра | 1-я цифра шифра | 2-я цифра шифра | 3-я цифра шифра | |||||
| а, м | b, м | с, м |  , м , м
| М, кНм | F, кН | q, кН/м | Номер схемы (рис. 5) | |
| 2.0 | 3,2 | 1,8 | ||||||
| 2,2 | 3,4 | 1,9 | ||||||
| 2.4 | 3,6 | 2,0 | ||||||
| 2,6 | 3,8 | 2,1 | ||||||
| 2,8 | 4,0 | 2,2 | ||||||
| 3,0 | 4,2 | 2,3 | ||||||
| 3,2 | 4,4 | 2,4 | ||||||
| 3,4 | 4,6 | 2,5 | ||||||
| 3,6 | 4,8 | 2,6 | ||||||
| 3,8 | 5,0 | 2,7 |
Пример решения задачи 9
Данная задача относится к теме «Поперечный изгиб». Задачи подобного типа возникают достаточно часто при расчете различных конструкций.
Прежде всего необходимо усвоить понятия «поперечная сила (Q)» и «изгибающий момент (M)» и научиться строить эпюры Q и M.
Поперечная сила Q в поперечном сечении балки численно равна алгебраической сумме проекций на плоскость сечения всех внешних сил, действующих по одну сторону от сечения.
Изгибающий момент М в поперечном сечении балки численно равен алгебраической сумме моментов (вычисленных относительно центра тяжести сечения) внешних сил, действующих по одну сторону от данного сечения.
Поперечная сила в сечении балки mn (рис. 6, а) считается положительной, если равнодействующая внешних сил слева от сечения направлена снизу вверх, а справа – сверху вниз, и отрицательной – в противном случае (рис. 6, б).

Рис. 6
Условие. Изгибающий момент М будем считать положительным, если в рассматриваемом сечении балка изгибается выпуклостью вниз (рис. 7, а), и отрицательным, если она изгибается выпуклостью вверх (рис. 7, б)
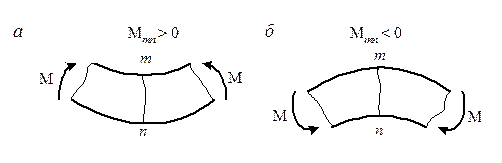
Рис. 7
Решение. Рассмотрим решение задачи № 9 по варианту, соответствующему шифру 000. По табл. 3 принимаем: схему 10; а = 3,8 м; b = 5,0 м; с = 2,7 м;  = 14,0 м; М = 11,0 кНм; F = 11 кН; q =13 кН/м.
= 14,0 м; М = 11,0 кНм; F = 11 кН; q =13 кН/м.
Определим опорные реакции RА и RВ (рис. 8, а):
Σ МА ( i) = 0;
i) = 0;
q·a·a/2 + M – RB·( – a – c) – F·(
– a – c) – F·( – a) = 0,
– a) = 0,
откуда
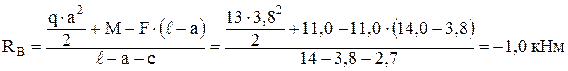 .
.
Знак «минус» означает, что направление реакции RВ выбрано неверно. Реакция RВ направлена вверх.

Рис. 8
Для определения реакции RA составим уравнение равновесия моментов относительно точки В:
Σ МВ ( i) = 0;
i) = 0;
q·a · ( – c – a/2) – RA · (
– c – a/2) – RA · ( – a – c) + M – F · c = 0;
– a – c) + M – F · c = 0;
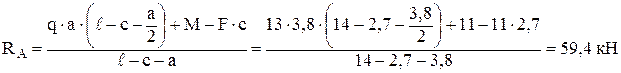 .
.
Проверим правильность определения реакций опор, для чего спроектируем все силы на ось y:
Σ Fy ( i) = 0;
i) = 0;
– q · a + RA – RB – F = – 13 · 3,8 + 59,4 – (–1) – 11 = 0.
Определим значения поперечных сил Q изгибающих моментов М на каждом участке балки, применяя метод сечений.
I участок:
QyI = – q · z.
Это уравнение прямой, поэтому достаточно вычислить значение поперечной силы в начале и конце участка, чтобы определить на эпюре Q ее значение в любой точке при 0 < z < a:
QyI|z=0 = 0;
QyI|z=a = − q · a =− 13 · 3,8 = − 49,4 кН;
МxI = − q · z · z/2;
МxI|z=0 = 0;
МxI|z=a = − q · a ·a / 2 = − 13 ·3,8 · 1,9 = − 93,9 кНм.
II участок:
QyII = − q · a + RA;
QyII|z=a= QyII|z=a+b= − 49,4 + 59,4 = 10 кН;
МxII = − q · a · (z − a /2) + RA · (z −a);
МxII|z=a = − q · a2 / 2 = − 13 · 3,82 /2 = − 93,9 кНм;
МxII|z=a+b = −q · a · (а/2 + b) + RA · b = − 13 · 3,8 · (3,8 / 2 + 5) =
= 59,4 · 5 = 43,9 кНм.
III участок:
QyIII = − q · a + RA;
QyIII|z=a+b= QyIII|z= −c = − 49,4 + 59,4 = 10 кН;
−c = − 49,4 + 59,4 = 10 кН;
МxIII = − q · a · (z − a /2) + RA · (z −a) − M;
МxIII|z=a+b = − q · a · (а/2 + b) + RA · b − M =
= − 13 · 3,8 · (3,8 / 2 + 5) =59,4 · 5 − 11= − 54,9 кНм;
МxIII|z= −c = − q · a · (
−c = − q · a · ( − c − a/2) + RA · (
− c − a/2) + RA · ( − c − a) − M =
− c − a) − M =
= − 13 · 3,8 · (14− 2,7 − 3,8/2) + 59,4· (14 − 2,7 − 3,8) − 11= − 29,7 кНм.
IV участок:
QуIV = − q∙a + RA – RB = − 49,4 + 59,4 + 1 = 11 кН;
МxIV = − q∙a· (z – a/2) + RA (z – a) – M – RB∙ (z –  + c);
+ c);
MxIV |z = – c = − q∙a∙ (
– c = − q∙a∙ ( − c − a/2) + RA∙ (
− c − a/2) + RA∙ ( − c – a) − M =
− c – a) − M =
= − 13 · 3,8 ∙ (14,0 − 2,7 − 3,8/2) + 59,4 (14 − 2,7−3,8) − 11 = − 29,7 кНм;
МxIV|z =  = − q∙a∙ (
= − q∙a∙ ( − a/2) + RA (
− a/2) + RA ( − a) − M − RB c =
− a) − M − RB c =
= − 13 · 3,8 (14 − 3,8/2) + 59,4 (14 – 3,8) − 11 + 1 · 2,7 = 0.
Построим эпюру Q (рис. 8, б). Следует обратить внимание на уравнение, согласно которому изменяется Q. На первом участке это уравнение прямой, проходящей через начало координат. При значении z = a Q принимает наибольшее значение. В точке А поперечная сила скачкообразно возрастает на величину RA и затем, как следует из уравнений для QУII и QУIII, остается неизменной до точки В, где скачкообразно возрастает на величину RB. На протяжении IV участка поперечная сила остается постоянной.
Аналогичный анализ уравнений изменения изгибающего момента на всех участках следует провести и при построении эпюры М (рис. 8, в). На участке I величина момента изменяется по параболе, причем выпуклость ее направлена вверх. Значения моментов на концах этого участка вычисляются при значениях z, равных соответственно 0 и а. На участках II – IV зависимость момента от координат точки на оси z линейная. В точке приложения сосредоточенного момента на эпюре М возникает скачок, равный его величине.
В целом при построении эпюр необходимо обратить внимание на следующую зависимость. На тех участках балки, где изгибающий момент изменяется по параболе (кривая 2-го порядка), поперечная сила изменяется по линейному закону, т. е. эпюра − наклонная прямая (линия первого порядка). Там же, где Ми изменяется по линейному закону (т. е. эпюра Ми – наклонная прямая), а поперечная сила Q постоянна, эпюра – горизонтальная прямая (линия нулевого порядка). Вообще порядок уравнения, описывающего закон изменения Q, на единицу ниже порядка уравнения, выражающего закон изменения Ми.
Как следует из эпюры Ми, опасное сечение будет расположено на опоре А, где действует максимальный изгибающий момент Мmax = 93,9 кНм.
Из условия прочности при изгибе
 σ =
σ =  ≤ [σ]
≤ [σ]
определим необходимый момент сопротивления балки:
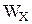 =
=  =
=  = 0, 626 · 10–3 м3= 626 см3.
= 0, 626 · 10–3 м3= 626 см3.
Согласно ГОСТ 8239 – 72 подбираем двутавр с моментом сопротивления Wx, ближайшим к вычисленному (приложение). Таковым является двутавр № 36, у которого Wx = 743 см3.
Вычислим максимальное нормальное напряжение в рассчитываемой балке:
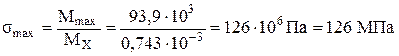 ,
,
что меньше допускаемого напряжения [σ] = 150 МПа.
При расчете консольно закрепленной балки (задача 10) можно использовать вышеизложенную методику решения задачи.
Задача 10. Тема «Поперечный изгиб»
Условие. Произвести расчет на прочность консольной балки (рис. 9). Материал балки – сталь с допускаемым напряжением при изгибе [σи]=200 МПа.
Требуется:
1) построить эпюры поперечных сил и изгибающих моментов;
2) определить размеры поперечного сечения балки: для круглого сечения –диаметр; для прямоугольного – значения сторон, считая, что отношение высоты сечения к его ширине равно двум.
Исходные цифровые данные представлены в табл. 4.

Рис. 9. Схемы к задаче 10
Таблица 4
| Цифра шифра | 1-я цифра шифра | 2-я цифра шифра | 3-я цифра шифра | |||
| F, кН | М, кНм | q, кНм | а, м | b, м | Номер схемы (рис. 9) | |
| 5,1 | 1,1 | 1,1 | ||||
| 5,6 | 0,6 | 0,6 | ||||
| 5,2 | 1,2 | 1,2 | ||||
| 5,7 | 0,7 | 0,7 | ||||
| 5,3 | 1,3 | 1,3 | ||||
| 5,8 | 0,8 | 0,8 | ||||
| 5,4 | 1,4 | 1,4 | ||||
| 5,9 | 0,9 | 0,9 | ||||
| 5,5 | 1,5 | 1,5 | ||||
| 6,0 | 1,0 | 1,0 |
Задача 11. Тема «Сложное сопротивление»
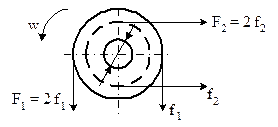
Условие. На валу закреплены три шкива: ведомый и два ведущих (рис. 10). Шкив диаметром D1, приводимый в движение вертикально расположенной ременной передачей, вращается с угловой скоростью ω и передает мощность Р1. Два других шкива имеют одинаковый диаметр D2 и передают вращательное движение посредством горизонтально расположенных ременных передач. Мощность, передаваемая каждым из ведущих шкивов, Р2 = 0,5 Р1. При расчете принять, что натяжение ведущих ветвей ремней в два раза больше, чем ведомых. Требуется:
1) определить моменты, приложенные к шкивам;
2) построить эпюру крутящих моментов Т;
3) найти реакции в опорах вала;
4) построить эпюры изгибающих моментов от горизонтальных и вертикальных сил;

| 
| ||
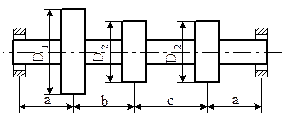
| 
| ||
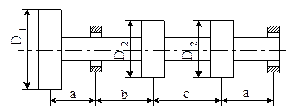
| 
| ||

| 
| ||
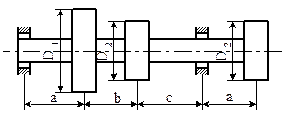
| 
| ||
|
Рис. 10. Схемы к задаче 11
5) найти опасное сечение и определить величину максимального эквивалентного момента (по третьей теории прочности);
6) найти диаметр вала d из условия, что [σ] =160 МПа.
Исходные цифровые данные представлены в табл. 5.
Таблица 5
| Цифра шифра | 1-я цифра шифра | 2-я цифра шифра | 3-я цифра шифра | |||||
| а, м | b, м | с, м | D1, м | D2, м | Р1, квт | ω, рад/с | Номер схемы (рис. 10) | |
| 1,1 | 1,0 | 0,9 | 0,6 | 0,2 | ||||
| 1,2 | 1,1 | 0,8 | 0,7 | 0,3 | ||||
| 1,3 | 1,2 | 0,7 | 0,8 | 0,4 | ||||
| 0,4 | 1,3 | 0,6 | 0,9 | 0,5 | ||||
| 0,5 | 0,4 | 0,5 | 1,0 | 0,6 | ||||
| 0,6 | 0,5 | 0,4 | 1,1 | 0,7 | ||||
| 0,7 | 0,6 | 1,0 | 1,2 | 0,8 | ||||
| 0,8 | 0,7 | 1,1 | 1,3 | 0,9 | ||||
| 0,9 | 0,8 | 1,2 | 0,4 | 1,0 | ||||
| 1,0 | 0,9 | 1,3 | 0,5 | 0,3 |
Пример решения задачи 11
Настоящая задача относится к задачам на расчет вала, испытывающего одновременно изгиб и кручение. Подобные задачи часто возникают при расчете различных передач (ременных, зубчатых, фрикционных).
Условие. Рассмотрим решение задачи по варианту, соответствующему шифру 000. По табл. 5 принимаем: схему 10 (см. рис. 10, 11, а); Р1 = 100 кВт; ω = 100 рад/с; а = 1 м; b = 0,9 м; с = 1,3; D1 = 0,5 м; D2 = 0,3 м; [σ] = 160 МПа.
Решение. Определим крутящие моменты, действующие на шкивы:
Т1 = Р1 /ω = 105 / 100 = 103 Нм = 1,0 кНм;
Т2 = Р2 /ω = 5 · 104 /100 = 5 · 102 Нм = 0,5 кНм.
По полученным значениям построим эпюру крутящих моментов Т по длине вала (рис. 11, б).
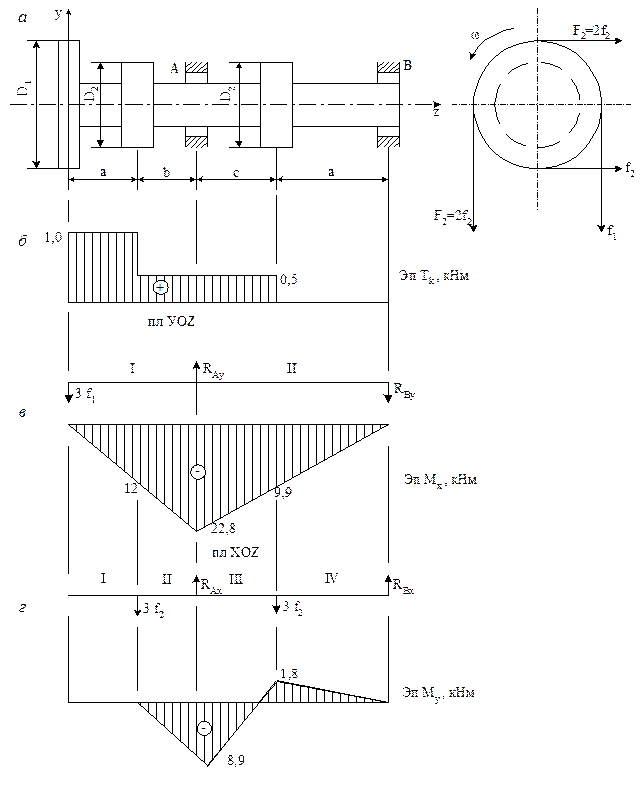
Рис. 11
Определим силы, воспринимаемые валом в результате действия натяжения ремней в вертикальной плоскости:
Т1 = (F1 − f1) D1/2 = (2f1 − f1) D1/2,
откуда
f1 = 2T1/D1 = 2·103/0,5 = 4·103 Н = 4 кН.
Определим реакции в опорах в вертикальной плоскости YOZ:
∑МА ( i) = 0;
i) = 0;
3f1∙ (a+b) − RBу ∙ (а + с) = 0;
RBу = 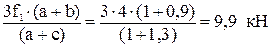 ;
;
∑МB ( i) = 0;
i) = 0;
3f1∙ (2a + b + c) − RAy ∙ (а + с) = 0;
RАy =  =
=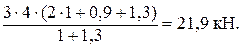
Проверка:
∑Fу = 0;
− 3 f1 + RАy − RВy = − 3 ·4 + 21,9 − 9,9 = 0.
Составим уравнения для определения изгибающих моментов на участках вала. Вал разделим на два участка. Наличие двух ведущих шкивов не учитываем, так как на них действуют силы в горизонтальной плоскости.
МхI = − 3f1 · z;
МхI|z = 0 = 0;
МxI|z = a + b = − 3f1 ∙ (a + b) = − 3 · 4∙ (1 + 0,9) = − 22,8 кНм.
МxII = − 3f1 · z + RАy = (z − (a +b));
МxII|z = a + b = − 3f1 · (a + b) = − 22,8 кНм;
МxII|z = 2a + b + c = − 3f1∙ (2a + b + c) + RAy · (2а + b + c − (a + b)) =
= − 3 · 4∙ (2 · 1 + 0,9 + 1,3) + 21,9 (1 + 1,3) = 0.
Определим силы, воспринимаемые валом в результате действия натяжения ремней в горизонтальной плоскости:
Т2 = (F2 − f2) ·  = (2f2 − f2) ·
= (2f2 − f2) ·  ;
;
f2 =  =
= 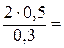 3,3 кН.
3,3 кН.
Определим реакции в опорах в горизонтальной плоскости XOZ:
∑MA (Fi) = 0; 3f2 · b – 3f2 · c + RBx· (a + c) = 0;
RBx = 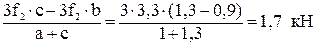 ;
;
∑MB ( i) = 0;
i) = 0;
3f2 (a + b + c) − RAx (a + c) + 3∙f2∙a = 0;
RAx = 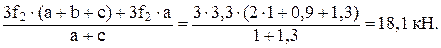
Проверка:
∑Fx = 0;
− 3f2 + RAx − 3f2 + RBx = − 3 · 3,3 + 1,7−3 · 3,3 + 18,1 = 0.
Составим уравнения для определения изгибающих моментов от горизонтально направленных сил. Вал разобьем на четыре участка.
MyI = 0;
МyII = − 3f2· (z − a);
MyII|z = a = 0;
МyII|z = a + b = − 3f2·b = − 3 · 3,3 · 0,9 = − 8,9 кНм;
МУIII = − 3f2 · (z − a) + RAx· (z − (a + b));
МyIII|z = a + b + c = − 3f2· (b + c) + RBx ·c = − 3 · 3,3· (0,9 + 1,3)·18,1·1,3 = 1,8 кНм;
МУIV = − 3f2 · (z − a) + RAx · (z − (a + b)) − 3f2 · (z – (a + b + c));
МyIV|z = 2a + b + c = − 3f2· (a + b + c) + RAx· (a + c) − 3f2 ·a =
= − 3 · 3,3 · (1 + 0,9 + 1,3) + 18,1· (1 + 1,3) − 3 · 3,3 · 1 = 0.
По результатам вычислений моментов в вертикальной и горизонтальной плоскостях построим эпюры МX и МУ.
По эпюрам Мx и Мy вычислим значения суммарных изгибающих моментов, используя равенство
М =  .
.
Вычислим значение суммарного изгибающего момента на границах участков:
М|z=0 = 0;
М|z = a = 12 кНм;
М|z = a + b = 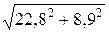 = 24,5 кНм;
= 24,5 кНм;
М|z = a + b + c = 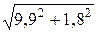 = 10 кНм;
= 10 кНм;
М|z = 2a + b + c = 0.
Как следует из совместного рассмотрения эпюр Т и М, опасное сечение вала расположено на опоре А. Вычислим эквивалентный момент, соответствующий этому сечению:
МА экв = 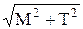 =
= 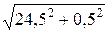 = 24,5 кНм.
= 24,5 кНм.
Из условия прочности
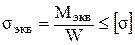
определим момент сопротивления сечения вала:
W = 
Зная, что момент сопротивления W при изгибе круглого сечения равен 0,1d3, определим диаметр вала:
d = 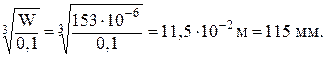
В соответствии с ГОСТ 6936–69 принимаем окончательно d = 120 мм.
 |
ЛИТЕРАТУРА
Основная:
1. Тарг С.М. Краткий курс теоретической механики: Учеб. для втузов.-19-е изд., стер.-М.: Высш.шк., 2009.- 416 с.: ил.
2. Сопротивление материалов: учеб.пособие/З.А.Наседкина, А.В.Песков, А.В. Шитиков.Екатеринбург: Изд-во ГОУ ВПО «Рос.гос.проф.-пед.ун-т», 2008, 135 с.
3. Колегова Е.Д., Наседкина З.А. Сборник задач по курсу «Сопротивление материалов». Екатеринбург: изд-во Рос.гос.проф-пед.ун-та, 2005.107 с.
Дополнительная:
1. Никитин Е.М. Теоретическая механика для техникумов.- 12-е изд., испр.- М.: Наука. Гл.ред.физ.-мат.лит., 1988.- 336 с.
2. Эрдеди А.А. и др. Техническая механика: Учеб. для техникумов / - 2-е изд. перераб.- М., Высш. школа, 1980.- 446 с., ил.
3. Ицкович Г.М., Минин Л.С.,Винокуров А.И. Руководство к решению задач по сопротивлению материалов: Учеб. пособие для вузов/ Под ред. Л.С. Минина.- 3-е изд., перераб. и доп.- М.: Высш. шк., 2001.- 592 с.: ил.
Задания и методические указания
для выполнения контрольных работ по дисциплине
«Теоретическая и прикладная механика»
и по дисциплине «Техническая механика»
(ГОС-2000).
Подписано в печать . Формат 60х84/16. Бумага для множ. аппаратов. Печать плоская. Усл. печ. л. ____ . Уч.- изд. л.___ . Тираж____ экз. Заказ____
ФГАОУ ВПО «Российский государственный профессионально-педагогический университет, Екатеринбург, ул. Машиностроителей, 11.
 |
Ризограф ФГАОУ ВПО РГППУ. Екатеринбург, ул. Машиностроителей, 11.
– Конец работы –
Используемые теги: Теоретическая, кладная, Механика0.073
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Теоретическая и прикладная механика
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов