Понятие о логике высказываний

Современная символическая логика для анализа дедуктивных рассуждений стро ит особые логические системы; одна из них называется логикой высказыванийилипропозициональной логикой,другая — логикой предикатов.Рассмотрим кратко принципы построения логики высказываний.

Логика высказываний — это логическая система, которая анализирует процессы рассуждения, опираясь на истинностные характеристики логических связок и отвлекаясь от внутренней структуры суждений.

Язык логики высказываний включает: алфавит, определение правильно выстроенных выражении, интерпретацию.

Алфавитidi ики Bbn - k . названий состоит изследующих символов.

Символы ,пя |!ыск<1)|,|»аний. р,q , r ... (пропозициональные переменные).
СИМВОЛЫ ДЛЯ .101 ИЧССМ1Х СВЯЗОК:

л — конъюнкция (союз ««»);

v — дизъюнкция (союз «или»);

—> — импликация (союз «если—, то...»);

= — эквивалентность (союз «если и только если..., то...»);

1 — отрицание («неверно, что...»). 3) Технические знаки (,) — скобки.

Допустимые в логике высказываний выражения, называемые правильно построенными формулами, или сокращенно ППФ,вводятся следующим определением:

Всякая пропозициональная переменная — р, q, г... — является ППФ.
Если А и В— ППФ(А и В — символы метаязыка для любых формул), то" выражения — А л В, А v В, А—>В, А = В,1А— также являются ППФ.
Все другие выражения, помимо предусмотренных п. 1 и 2, не являются ППФязыка логики высказываний.

Логика высказываний может строиться табличным методомили как исчисление,т.е. как система, позволяющая получать по правилам вывода из одних формул другие.

Табличное построение предполагает семантические определения пропозициональных связок в виде матриц, показывающих зависимость истинного значения сложных формул от значений их составляющих простых формул. Если А и В простые формулы, то истинное значение построенных с помощью логических связок формул может быть представлено матричным способом — в виде таблицы (см. рис. 36).

Среди правильно построенных формул в зависимости от их истинностного значения различаюттождественно истинные, тождественно ложныеивыполнимые формулы.

Тождественно истинныминазывают формулы, принимающие значения истины при любых— истинных или ложных—значениях составляющих их пропозициональных переменных. Такие формулы представляют собой законы логики.

Тождественно ложныминазывают формулы, принимающие значение ложности при любых — истинных или ложных — значениях пропозициональный переменных.

Выполненныминазывают формулы, которые могут принимать значения истинности или ложности в зависимости от наборов значений составляющих их пропозициональных переменных.

Табличное построение предполагает определение логических отношений между формулами. Существенное значение для анализа рассуждений имеет отношение логического следования (символ |—). которое определяется следующим образом. Из Ai ,..., An как посылок логически следует В как заключение, если при истинности каждого Ai, ..., An истинным является и В. В языке-объекте отношение следования адекватно выражается импликацией. Значит, если Ai,..., Ап г-В> то формула, представляющая собой импликацию вида (Ai л ai л ... л An ) —> В,должна быть тождественной истинной.

Табличное носгроение логики высказываний позволяет определять логические отношения между высказываниями (см. гл. V § 4) и проверять правильность умозаключений, используя приведенный выше критерий. В качестве примера предлагаем провести табличным способом проверку правильности рассуждения формулы (р —> q ) )- (1 q —> 1 p ). Заменив знак логическою следования между посылкой и заключением па импликацию и построив таблицу для полученной формулы, видим, что она является тождественно истинной. Значит, рассуждение является правильным.

Если в рассуждении содержится более трех переменных, то строить полную таблицу для проверки его правильности затруднительно и тогда используют сокращенный метод проверки, рассуждая от противного. Поскольку при правильном рассуждении формула вида (Ai л ... л An ) —> В должна быть тождественно истинной, посмотрим, не может ли она при каком-то наборе значений неременных оказаться ложной. Допустим, что может. Если из этого допущения получим какое-нибудь противоречие, то такое допущение будет неверным, а проверяемое рассуждение — правильным. Если же из допущения не получаем противоречия, то обнаружим набор значений переменных, при котором формула ложна, т.е. тот набор, который опровергает проверяемое рассуждение.

Логика высказываний как исчисление— это прежде всего так называемая система натурального вывода(СНВ).Аппаратом в ней служат правила вывода, каждое из которых является какой-нибудь элементарной формой умозаключения. Переходя по этим правилам от посылок или некоторых допущений к новым формулам, постепенно доходят до заключения. Вывод из посылок осуществлен, если удалось элиминировать все сделанные допущения. Таким образом, поавыводом формулы В(заключения) из формулAi,..., А„ (посылок) имеется в виду последовательность формул, каждая из которых является либо посылкой, либо допущением, либо получается по правилам вывода из предыдущих, и последняя формула этой последовательности есть формула В, а все допущения при этом элиминированы.

Правила СНВ позволяют оперировагь со всеми связками, имеющимися в алфавите языка. Они делятся на правила введения(в) и правила исключения(и) связок.

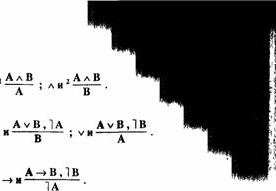
НА ' А •