Скатывание тел с наклонной плоскости - раздел Механика, Курс общей физики (лекции) Раздел I Физические основы механики С Тем, Чтобы Проиллюстрировать Применение Законов Динамики Твёрдого Тела, Реш...
С тем, чтобы проиллюстрировать применение законов динамики твёрдого тела, решим задачу о скатывании цилиндра с наклонной плоскости (рис. 10.5).
Сплошной цилиндр массы m и радиуса R скатывается без проскальзывания с наклонной плоскости. Угол наклона плоскости — a, а высота Н (Н » R). Начальная скорость цилиндра равна нулю. Определим время скатывания — Т и скорость центра масс цилиндра у основания наклонной плоскости.
При качении цилиндра на него действуют три силы: сила тяжести 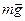 , упругая сила реакции опоры
, упругая сила реакции опоры  и сила трения покоя
и сила трения покоя 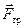 (ведь качение без проскальзывания!).
(ведь качение без проскальзывания!).
Представим это движение суммой двух движений: поступательного со скоростью VC, с которой движется ось цилиндра, и вращательного вокруг оси цилиндра с угловой скоростью w.
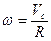 . (10.9)
. (10.9)

Рис. 10.5
Эта связь скоростей поступательного и вращательного движений следует из условия «движение без проскальзывания».
Продифференцировав уравнение (10.9) по времени, получим соотношение углового и линейного ускорений цилиндра:
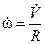 , то есть
, то есть 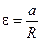 .
.
Воспользовавшись теоремой о движении точки центра масс, опишем поступательное движение цилиндра:
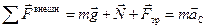 . (10.10)
. (10.10)
Для описания вращения воспользуемся основным уравнением динамики вращательного движения:
MC = IC × e. (10.11)
Спроецировав уравнение (10.10) на направления осей x и y, получим два скалярных уравнения:
x: mgSina – Fтр = maC; (10.12)
y: N – mgсosa = 0. (10.13)
Обратимся теперь к уравнению (10.11). Из трёх названных сил момент относительно оси цилиндра создаёт только сила трения:
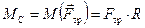 .
.
Момент инерции сплошного цилиндра относительно его оси равен (см. лекцию №9):
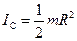 .
.
Учитывая всё это, уравнение (10.11) перепишем так:
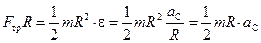 . (10.14)
. (10.14)
Решая совместно уравнения (10.12) и (10.14), получим следующие значения неизвестных величин:
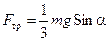 ; (10.15)
; (10.15)
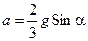 . (10.16)
. (10.16)
Из уравнения (10.15) следует, что с увеличением угла наклона a должна возрастать и сила трения покоя Fтр. Но, как известно, её рост ограничен предельным значением:
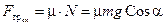 . (10.17)
. (10.17)
Так как сила трения покоя (10.15) не может превышать предельного значения (10.17), то должно выполняться неравенство:
⅓mgSina ≤ mmgCosa.
Отсюда следует, что скатывание будет происходить без проскальзывания до тех пор, пока угол a не превзойдёт значения aпред:
aпред = arctg3m.
Здесь m — коэффициент трения цилиндра по плоскости.
Линейное ускорение цилиндра (10.16) величина неизменная, следовательно, поступательное движение цилиндра равноускоренное. При таком движении без начальной скорости цилиндр достигнет основания наклонной плоскости за время:
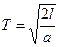 .
.
Здесь: l = 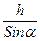 — длина плоскости;
— длина плоскости;
a =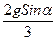 , (см.10.16).
, (см.10.16).
Значит, время скатывания:
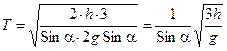 . (10.18)
. (10.18)
Вычислим конечную скорость поступательного движения оси цилиндра:
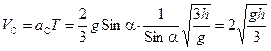 . (10.19)
. (10.19)
Заметим, что эту задачу можно решить проще, воспользовавшись законом сохранения механической энергии.
В системе, правда, присутствует сила трения, но её работа равна нулю, поскольку точка приложения этой силы в процессе спуска остаётся неподвижной: ведь движение происходит без проскальзывания. Раз нет работы силы трения, механическая энергия системы не меняется.
Рассмотрим энергию цилиндра в начальный момент — на высоте h и в конце спуска. Полная энергия цилиндра в этих положениях одинакова:
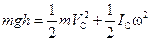 .
.
Вспомним, что 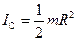 и
и 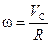 . Тогда уравнение закона сохранения энергии можно переписать так:
. Тогда уравнение закона сохранения энергии можно переписать так:
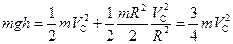 .
.
Отсюда легко найдём конечную скорость цилиндра:
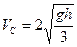 ,
,
которая блестяще подтверждает полученный нами ранее результат (10.19).
Лекция 11 «Элементы механики жидкости»
План лекции
1. Давление жидкости. Законы гидростатики.
2. Стационарное течение жидкости. Уравнение неразрывности потока.
3. Основной закон динамики для идеальной жидкости. Уравнение Бернулли.
4. Применение уравнения Бернулли для решения задач гидродинамики.
4.1. Истечение жидкости из сосуда.
4.2. Манометрический расходомер.
Все темы данного раздела:
Москва, 2003
Лекция 1 «Кинематика материальной точки»
План лекции.
1. Введение. Физика — основа современного естествознания.
1.1. Из истории меха
Из истории механики
Скорость движения
Систему координат выберем так, чтобы одна из осей (например, х) совпала с прямолинейной траекторией движения. При таком выборе две другие координаты частицы М меняться не будут y
Ускорение
В общем случае прямолинейного движения скорость материальной точки может меняться во времени: V = V(t).
Пусть в момент времени t1 скорость была V
Равномерное движение
Равномерным называется движение частицы, если её координата является линейной функцией времени
x(t) = A + B t. (1.9)
Здесь А и В — постоянные величины.
Равнопеременное движение
Равнопеременным называется движение материальной точки, если её координата является квадратичной функцией времени
х = А +В t + С t2. (1.13)
Раскрое
Сложение (вычитание) векторов
(2.1)
Сложение векторов производится по правилу параллелограмма (рис. 2.
Скалярное произведение двух векторов.
По определению скалярным произведением векторов и
Векторное произведение
Результатом векторного произведения векторов и
Производная вектора
Пусть вектор меняется по известному закону со временем.
Скорость движения
Зададим криволинейное движение частицы М зависимостью её радиус-вектора от времени (рис. 2.7):
Ускорение. Нормальное и тангенциальное ускорение. Радиус кривизны траектории
Движение по криволинейной траектории всегда происходит с переменной скоростью. Пусть
Движение материальной точки по окружности
Положение частицы М, движущейся по окружности радиуса R, можно задать в любой момент времени углом поворота её радиус-вектора j = j(t) (рис. 2.14). Угол j отсчитывается от наперёд выб
Первый закон Ньютона
Существуют системы отсчёта, в которых свободные частицы движутся прямолинейно и равномерно, либо остаются в состоянии покоя.
Свободными называются тела, не испытывающие действия со стороны
Второй закон Ньютона. Сила
Введя понятие «импульс тела», можно так сформулировать первый закон Ньютона: если на тело не действуют никакие другие тела, его импульс остаётся постоянным.
Значит, изменение импуль
Третий закон Ньютона
Действие одного тела на другое носит характер взаимодействия, в котором возникают две силы: действия
Силы в природе
Всё многообразие сил в природе можно свести к четырём типам взаимодействий: 1) гравитационному, 2) электромагнитному, 3) ядерному сильному и 4) ядерному слабому.
Два первых взаимодействия
Сухое трение
Приложим «небольшую» силу к телу, лежащему на горизонтальной поверхности. «Небольшую» — то есть, недостаточную для начала движения. Тело будет оставаться в покое, потому что кроме приложенной нами
Вязкое трение
Сила вязкого трения действует на тело, движущееся в вязкой среде (жидкой или газообразной). Она зависит от формы и размеров тела, скорости его движения, а также от физических свойств среды: в частн
Упругие силы. Закон Гука
Упругими называются силы, возникающие при упругих деформациях тел.
Рассмотрим зависимость деформации металлического стержня или струны от величины внешней растягивающей силы F (рис.
Закон сохранения импульса
Импульс тела — вектор, равный произведению массы этого тела на его скорость:
Теория о движении центра масс
Рассмотрим движение системы «n» взаимодействующих частиц.
Центром масс системы называется точка, радиус-вектор которой отвечает следующему условию
Движение тел переменной массы. Реактивное движение
До сих пор мы считали, что масса тел в процессе их движения не меняется. Но так обстоит дело не всегда.
Рассмотрим, например, движение ракеты — классический пример тела, масса которого уме
Работа и кинетическая энергия
По определению, элементарной работой силы на бесконечно малом перемещении
Консервативные и неконсервативные силы
Консервативными называются силы, работа которых не зависит от формы траектории, а определяется только положением её начальной и конечной точек.
К классу консервативных относятся, например,
Потенциальная энергия
Состояние механической системы характеризуют потенциальной энергией, если на систему действуют только консервативные силы.
Рассмотрим два состояния системы: потенциальную энергию в одном и
Механическая энергия. Закон сохранения механической энергии
На прошлой лекции было введено понятие потенциальной энергии системы.
По определению разность потенциальных энергий системы в двух состояниях равна работе, совершаемой консервативными сила
Работа неконсервативных сил
Рассмотрим систему n материальных частиц.
Пусть при их взаимодействии друг с другом возникают только консервативные силы
Силы и потенциальная энергия
Эту лекцию мы начали с вычисления потенциальной энергии упруго деформированной пружины. Зная характер силы, возникающей при деформации пружины — закон Гука — мы смогли вычислить её энергию.
Момент силы и момент импульса относительно неподвижного центра и неподвижной оси
Рассмотрим движение материальной точки m под действием силы . Положение это
Уравнение моментов для материальной точки и системы материальных точек
Рассмотрим систему двух взаимодействующих частиц (рис. 8.4). На этом рисунке и
Закон сохранения момента импульса
Анализируя уравнение моментов относительно произвольного центра и неподвижной оси, мы говорили уже об условиях, при которых момент импульса системы не будет меняться во времени.
Сформулиру
Модель твердого тела в механике. Поступательное и вращательное движение твердого тела
Все тела под действием приложенных сил деформируются, то есть в большей или меньшей степени меняют свою форму и размеры. Если эти деформации незначительны и не оказывают влияния на движение тела, т
Основное уравнение динамики вращательного движения вокруг неподвижной оси
При вращении твёрдого тела относительно неподвижной оси, все точки тела движутся по плоским круговым траекториям. Выделим частицу mi тела, вращающегося вокруг оси z (рис. 9
Теорема Гюйгенса-Штейнера
Момент инерции тела относительно произвольной оси (I) равен сумме момента инерции Ic относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тел
Полная система уравнений, описывающая произвольное движение твердого тела. Условия его равновесия и покоя
Как уже отмечалось, произвольное движение твердого тела может быть представлено совокупностью двух простых движений: поступательного и вращательного. Причем деление произвольного движения на состав
Энергия движущегося тела
2.1. Кинетическая энергия твёрдого тела, вращающегося вокруг неподвижной оси
В твёрдом теле, вращающемся с угловой скоростью w относительно неподвижной оси z, выдел
Кинетическая энергия тела при плоском движении
Любое движение твёрдого тела может быть представлено суперпозицией двух движений — поступательного и вращательного.
Представим плоское движение тела суммой поступательного со скоростью
Давление жидкости. Законы гидростатики
Твёрдые тела обладают упругостью объёма и формы. Это означает, что упругие силы сопротивления препятствуют любым изменениям объёма и формы твёрдого тела.
Особенности молекулярного строения
Стационарное течение жидкости. Уравнение неразрывности
Параметры текущей жидкости — скорость, плотность, давление и другие — в общем случае являются функциями времени и положения точки в потоке. Если они не зависят от времени, то есть остаются постоянн
Основной закон динамики для идеальной жидкости. Уравнение Бернулли
При течении жидкости между её отдельными частицами возникают силы вязкого сопротивления. В газах эти силы сравнительно невелики, и ими можно пренебречь. Однако и во многих случаях течения жидкости
Уравнение Бернулли
Рассмотрим стационарное течение идеальной жидкости. Выделим в потоке трубку тока, а в ней — объём, ограниченный стенками трубки и двумя сечениями S1 и S2 (рис. 1
Истечение жидкости из сосуда
Вычислим скорость истечения жидкости через отверстие в сосуде (рис. 11.7). Выделим в толще жидкости трубку тока. При этом не важна конфигурация этой трубки, важно, что одно её сечение расположено н
Манометрический расходомер
Вычислим секундный расход жидкости, протекающей по горизонтальной трубе. Для этого вмонтируем в трубопровод расходомер в виде локального сужения трубы (рис. 11.8).
Периодические процессы. Гармонические колебания
Периодическими называются процессы, в точности повторяющиеся через равные промежутки времени: смена дня и ночи, движение поршня в цилиндре двигателя, колебание маятника часов, переменный ток и т.д.
Собственные незатухающие колебания
Классифицируя колебания, их делят, прежде всего, на собственные и вынужденные. Представить себе собственные колебания осциллятора очень просто: отведите из положения равновесия обычны
Пружинный осциллятор
Пружинный маятник — это грузик массой m, прикреплённый к пружине жесткостью k. Грузик может двигаться вдоль оси x по горизонтальной поверхности без трения (рис. 12.4). Начало отсчета
Математический маятник
Математический маятник — это идеализированная система, представляющая собой материальную точку на невесомой и нерастяжимой нити. Хорошим приближением к этой модели является маленький тяжелый шарик
Собственные колебания физического маятника
Физическим маятником можно назвать любое твердое тело, совершающее колебания под действием силы тяжести вокруг неподвижной точки или оси. Возьмём в качестве такого маятника однородный тонкий стерже
Сложение гармонических колебаний. Метод векторных диаграмм
Гармоническое колебание x = a Cos (wt + a) геометрически может быть представлено проекцией на произвольное направление x вектора
Энергия гармонического осциллятора
Собственные незатухающие колебания возникают в системе при выполнении двух условий: во-первых, при смещении из положения равновесия должна возникать возвращающая сила, пропорциональная смещению (уп
Собственные затухающие колебания
До сих пор мы рассматривали колебательные процессы в системах, где действовала одна единственная сила — упругая или квазиупругая («как упругая»). Уравнение такого движения записывается просто:
Вынужденные колебания. Резонанс. Амплитуда и фаза вынужденных колебаний
Рассмотрим колебания, которые поддерживаются в системе внешней гармонической силой F = F0Coswt. Такие колебания называются вынужденными.
Обратимся вновь к п
Постулаты специальной теории относительности. Преобразования Лоренца
В релятивистской механике, также как и в классической, предполагается, что время однородно, а пространство однородно и изотропно.
Фундаментом специальной теории относительности являются дв
Основное уравнение релятивистской динамики
Экспериментально установлено, что в области релятивистских скоростей становится заметной зависимость массы частицы от скорости
Закон эквивалентности массы и энергии
В соответствии с законом Эйнштейна полная энергия системы пропорциональна её релятивистской массе:
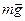 , упругая сила реакции опоры
, упругая сила реакции опоры  и сила трения покоя
и сила трения покоя 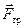 (ведь качение без проскальзывания!).
(ведь качение без проскальзывания!).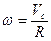 . (10.9)
. (10.9)
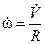 , то есть
, то есть 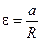 .
.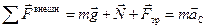 . (10.10)
. (10.10)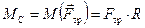 .
.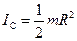 .
.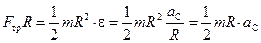 . (10.14)
. (10.14)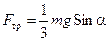 ; (10.15)
; (10.15)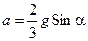 . (10.16)
. (10.16)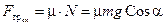 . (10.17)
. (10.17)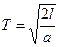 .
.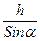 — длина плоскости;
— длина плоскости;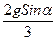 , (см.10.16).
, (см.10.16).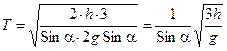 . (10.18)
. (10.18)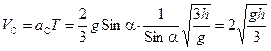 . (10.19)
. (10.19)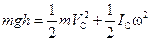 .
.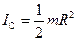 и
и 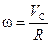 . Тогда уравнение закона сохранения энергии можно переписать так:
. Тогда уравнение закона сохранения энергии можно переписать так: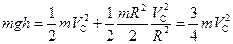 .
.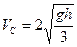 ,
,






Новости и инфо для студентов