Некоторые соотношения, полезные при вычислении момента инерции

1. Теорема Штейнера. Момент инерции I относительно произвольной оси равен сумме момента инерции 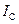относительно оси, параллельной данной и проходящей через центр масс С тела, и произведения массы тела на квадрат расстояния а между осями: .

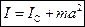Например: для диска относительно оси, проходящей через край с учётом полученного выше соотношения: .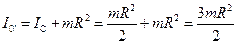

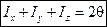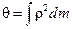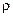2. Сума моментов инерции тела относительно 3-х взаимно перпендикулярных осей, пересекающихся в одной точке = удвоенному моменту инерции этого тела относительно той же точки : , , где – расстояние от участка с массой 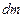до точки.

Например: для сферы массы m, радиуса R: 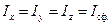, 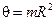(расстояние от любой точки до центра одинаково); тогда , откуда .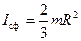

3. Для плоской фигуры, лежащей в плоскости xy: 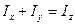(следствие из 2).

Например: для кольца массы m, радиуса R: 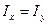, а 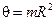(расстояние от любой точки до центра одинаково); ,

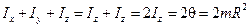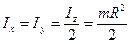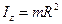, (такое значение 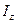может быть получено из более простых рассуждений, таких же, как для ).

Для диска: .

Моменты инерции некоторых однородных тел простой формы относительно оси, проходящей через центр масс (некоторые соотношения выведены выше):

· Тонкий стержень длины 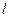(ось перпендикулярна стержню)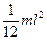

· Сплошной цилиндр (диск) радиуса R (ось совпадает с осью симметрии)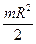

· Тонкий диск радиусом R (ось совпадает с диаметром)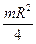

· Шар радиуса R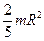

· Сфера радиуса R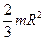

Кинетическая энергия твердого тела при плоском движении:

.

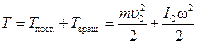Решение задач на вращение твердого тела вокруг неподвижной оси аналогично по форме решению задач на поступательное движение (движение точки) при замене в формулах линейных величин на угловые: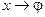

.

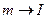
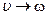
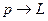
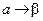
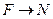Поступательное движение		Вращательное движение
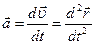
	Скорость и перемещение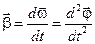
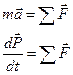
	Основное уравнение динамики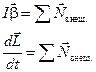
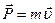
	Импульс, момент инерции
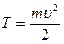
	Кинетическая энергия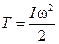
	Работа внешних сил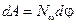

Механические колебания