МАТРИЦА ПЛОТНОСТИ

 

Если нет полной информации о системе, то она не имеет волновой функции и описывается матрицей плотности, введенной Л.Д. Ландау и Дж. фон Нейманом в 1927 г.

Чистое и смешанное состояния. Чистое состояние описывается волновой функцией. Для смешанного состояния известна лишь вероятность того, что состояние описывается одной из возможных волновых функций . Между этими функциями не определены фазовые соотношения и отсутствует интерференция. Например, если параметр системы измерен не точно, то состояние смешанное и является вероятностью i-ого значения параметра. Так, если в атоме водорода положение протона не фиксировано, то электрон находится в смешанном состоянии. Если протон неподвижен или его движение упорядочено, то состояние электрона чистое. Чистое состояние разлагается по ортонормированному базису с коэффициентами, которые могут регулярно изменяться. Если коэффициенты изменяются беспорядочно, то состояние смешанное. Чистое состояние переходит в смешанное в процессе декогеренциисистемы, когда она взаимодействует с объектом, испытывающим хаотические изменения, например, с макроскопическим телом. Декогеренция ускоряется с увеличением размеров квантовой системы. Система в чистом состоянии должна быть изолирована от окружающих тел и хаотически меняющихся полей путем охлаждения, вакуумирования и экранирования. Уменьшение декогеренции необходимо для квантового компьютера и квантовой криптографии. Смешанное состояние описывается матрицей плотности, чистое состояние – как волновой функцией, так и матрицей плотности.

 

Матрица плотности чистого состояния. Состояние 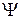разлагаем по собственным функциям 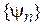некоторого эрмитового оператора

 

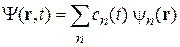
и описываем набором коэффициентов 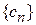. Для среднего значения величины a получаем

, (2.76)

где

– матричный элемент оператора между состояниями и .

Определяем матрицу плотности r с элементами

 

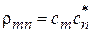, (2.77)

тогда

, (2.78)

где

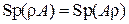– шпур (от нем. die Spur – «след») – сумма диагональных элементов матрицы;

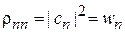является вероятностью обнаружения состояния в состоянии .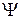

При 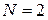получаем

,

,

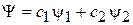где

;

 

;

 

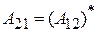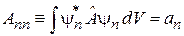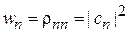– вероятность результата .

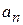Наличие интерференционного слагаемого 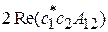означает, что y₁ и y₂ в составе чистого состояния взаимно согласованы по фазе, т. е. когерентные. Их интерференция влияет на результат.

 

Матрица плотности смешанного состояния. Для смешанного состояния коэффициенты разложения зависят от не полностью определенного параметра состояния j. В (2.76) появляется дополнительное усреднение по j

,

 

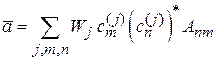где 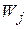– вероятность j-ого значения. Определяем матрицу плотности в виде среднего по j

 

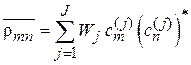, (2.79)

тогда (2.78) сохраняет форму

 

.

Диагональный элемент

дает вероятность состояния ;

является вероятностью состояния в компоненте j смешанного состояния.

Недиагональные элементы (2.79) характеризуют корреляцию состояний m и n.

При , получаем

 

.

 

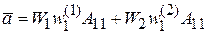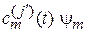Интерференционный член отсутствует, поэтому волновые функции компонент и смешанного состоянияне когерентные.

 

Свойства матрицы плотности:

 

Условие нормировки

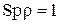. (2.80)

 

Условие эрмитовости

. (2.81)

 

 

Признак чистого состояния

. (2.82)

 

При нарушении (2.82) состояние смешанное.

 

Уравнение фон Неймана

 

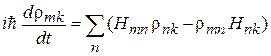(2.83)

 

является аналогом уравнения Шредингера для смешанного состояния.