рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Механика
- /
- МЕХАНИКА И ТЕРМОДИНАМИКА
Реферат Курсовая Конспект
МЕХАНИКА И ТЕРМОДИНАМИКА
МЕХАНИКА И ТЕРМОДИНАМИКА - раздел Механика, Министерство Образования И Науки Российской Федерации ...
Министерство образования и науки Российской Федерации
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––
53 № 3248
М 55
МЕХАНИКА И ТЕРМОДИНАМИКА
Методические указания
по физике для студентов I курса всех факультетов НовосибирскОГЛАВЛЕНИЕ
ВВЕДЕНИЕ.......................................................................................................................... 4
Лабораторная работа № 0. ОПРЕДЕЛЕНИЕ ОБЪЕМА ТЕЛА
ЦИЛИНДРИЧЕСКОЙ ФОРМЫ........................................................................ 26
Лабораторная работа № 1. ИЗМЕРЕНИЕ СКОРОСТИ ПУЛИ
С ПОМОЩЬЮ БАЛЛИСТИЧЕСКОГО МАЯТНИКА................................ 30
Лабораторная работа № 3. ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ
МАЯТНИКА ОБЕРБЕКА.................................................................................. 38
Лабораторная работа № 4 ОПРЕДЕЛЕНИЕ МОМЕНТА
ИНЕРЦИИ ТЕЛА.................................................................................................. 45
Лабораторная работа № 5. ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛА
МЕТОДОМ КОЛЕБАНИЙ................................................................................ 58
Лабораторная работа № 6. ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ АДИАБАТЫ
МЕТОДОМ КЛЕМАНА И ДЕЗОРМА............................................................ 64
Введение
В лабораторном практикуме Вы постоянно будете иметь дело с измерениями физических величин. Необходимо уметь правильно обрабатывать и представлять результаты этих измерений. Цель данного раздела – сообщить основные сведения, касающиеся особенностей физических измерений, обработки и представления результатов. Для более полной и детальной информации следует обращаться к специальной литературе, например [1–5].
В.1. Погрешности измерений физических величин
Под измерением понимается операция, в результате которой определяется, во сколько раз интересующая нас величина больше или меньше величины той же природы, принятой за единицу.Таким образом, измерение является актом сравнения: расстояние сравнивается с единицей расстояния, время – с единицей времени, ток – с единицей тока и т. д. Единицы измерения при этом должны быть предварительно определены. В лабораторном практикуме необходимо придерживаться международной системы единиц СИ.
Часто одну и ту же величину можно измерить разными способами. Например, высоту здания можно измерить с помощью:
1) рулетки;
2) секундомера, определив время свободного падения небольшого по размерам металлического шарика;
3) рулетки, угломера и лазера, определив расстояние от здания
до лазера и угол, под которым лазерный луч направлен на вершину здания;
4) и т. д.
Анализируя подобные ситуации, можно прийти к следующему выводу.
Измерения бывают прямыми и косвенными. В случае прямого измерения значение искомой величины непосредственно определяется с помощью прибора, шкала которого проградуирована в единицах измерения этой величины. В случае косвенного измерения значение величины вычисляется по формуле, которая связывает искомую величину с другими, измеренными прямо или косвенно.
Очевидно, в нашем примере первое измерение высоты является прямым, а второе и третье – косвенными.
Измерение можно проводить как однократно, так и многократно, пытаясь воспроизвести одни и те же условия.
Если мы произведем многократные измерения высоты здания последовательно каждым из трех способов, то сравнение результатов измерений между собой приведет нас к очень интересным и важным выводам:
1. Результаты измерений первым способом могут отличаться от результатов измерений вторым способом, а последние, в свою очередь, от результатов измерений третьим способом и т. п.
Разные способы измерения одной и той же величины могут давать разные ее значения.
Результаты многократных измерений с помощью одного и того же способа тоже могут отличаться друг от друга. Многократные измерения одной и той же величины одним и тем же способом могут дать разные ее значения.
Проанализируем сложившуюся ситуацию.
Сначала выясним, почему разные способы измерения одной и той же высоты привели к разным результатам.
На первый взгляд, первый способ – самый надежный. Мы прикладываем ленту рулетки к поверхности здания и определяем искомую высоту. Более внимательный анализ показывает, что это не совсем так. Оказывается, здание построено с небольшим наклоном, а стена в том месте, где производятся замеры, имеет определенную кривизну – она выпуклая, причем в сторону улицы. Это означает, что мы измеряли не высоту здания, а длину стены, связанную с высотой.
Второй способ представляет собой косвенное измерение. Измерив время падения шарика, мы рассчитываем высоту по известной формуле для свободного падения: h = gt2/2. На этот раз измерение действительно касается высоты. Но мы забыли о том, что шарик движется в воз-духе и, следовательно, испытывает сопротивление среды. Поэтому рассчитанная по формуле величина также не является истинным значением высоты здания.
Третье измерение, как и второе, является косвенным. Высота определяется из геометрических соображений: в прямоугольном треугольнике длина противолежащего катета равна произведению длины прилежащего катета на тангенс угла. В нашем случае высота играет роль одного катета, а расстояние от лазера до здания – роль другого. На этот раз нас подвело предположение об идеально горизонтальной поверхности, на которой стоит здание. Результат – опять измерена величина, не являющаяся высотой, но теперь по другой причине.
Итак, в каждом способе измерения присутствуют какие-то постоянные факторы (в каждом случае свои, причем их может быть несколько), которые приводят к появлению систематической погрешности измерения данным способом. Каждый раз при измерении значения одной и той же величины в одних и тех же условиях систематическая погрешность имеет одно и то же значение. Если эти факторы учесть, введя соответствующие поправки, то можно приблизиться к реальному значению измеряемой величины, и тогда результаты измерений разными способами (с учетом поправок на систематическую погрешность) могут оказаться довольно близкими. Таким образом,
в принципе систематические погрешности могут быть учтены и даже исключены, хотя осуществление этого на практике может оказаться довольно непростой задачей.
Теперь попытаемся выяснить, почему многократные измерения одной и той же высоты одним и тем же способом (включая один и тот же комплект приборов) могут приводить к отличающимся друг от друга значениям. Это связано с целым рядом факторов, действующих случайным образом. В рассмотренном примере могут быть небольшие механические колебания почвы, здания и приборов, тепловые воздействия, связанные с изменением линейных размеров стены и используемых приборов, и т. п. Наконец, есть еще человеческий фактор, связанный с восприятием происходящих процессов и реакцией на это восприятие. В результате при повторных измерениях одной и той же величины могут получаться различные ее значения, связанные со случайными погрешностями. От измерения к измерению случайная погрешность может изменять как свой знак, так и свою величину. В силу случайного характера воздействий заранее предсказать величину такой погрешности невозможно.
Наш анализ вызывает закономерные вопросы:
1. Что такое «истинное» значение измеряемой величины?
2. Как представлять результаты измерений с учетом погреш-ностей?
Поскольку эти вопросы касаются не только рассмотренного примера, но и любых других измерений, мы перейдем к обобщениям и выработке общих рекомендаций.
Приведенный конкретный пример продемонстрировал общее свойство, характерное для любых измерений, – любое измерение сопровождается погрешностями.
Это свойство, в конечном счете, обусловлено тем, что всякое измерение предполагает определенную взаимосвязанную цепочку участников процедуры измерения: наблюдатель – измерительный прибор – анализируемый объект – «внешняя среда».
Элементы этой цепочки связаны огромным количеством взаимодействий и движений. В процессе измерения анализируемый объект, измерительный прибор и наблюдатель могут быть подвержены различным влияниям (в том числе и взаимным), что и сказывается на результате измерений.
Безусловно, если уменьшать влияния, не имеющие непосредственного отношения к процедуре измерения, и стараться учитывать неустранимые влияния, то точность наших измерений будет возрастать. Но абсолютно точное измерение невозможно принципиально. И это во многом связано с природой самих измеряемых величин.
Если мы, например, захотим абсолютно точно измерить длину металлического стержня, то обнаружим наличие принципиально неустранимых (хотя и очень малых) колебаний кристаллической решетки. Никакой абсолютно точной «истинной» длины у стержня нет. Она постоянно случайным образом изменяется, отклоняясь в ту или иную сторону от некоторого наиболее часто встречающегося значения. Вот это значение мы можем принять за «истинное» значение длины и в дальнейшем оперировать именно им, говоря о длине стержня, или используя эту величину для каких-либо расчетов, например для определения объема стержня.
Такого рода ситуация обнаруживается во множестве других измерений. Сами измеряемые величины случайным образом могут изменяться, что обусловлено, как уже сказано выше, физической природой этих величин. Таким образом, мы сталкиваемся с принципиальной неустранимостью случайных факторов. Их можно свести к минимуму, но окончательно избавиться от них нельзя. Следовательно, представляя результаты измерений, мы должны давать информацию, касающуюся нашей оценки «истинного» значения величины
с учетом случайных погрешностей измерения (при условии, что систематическая погрешность исключена или учтена в виде соответствующей поправки). Понятно, что наиболее полно такая информация может быть представлена по результатам многократных измерений.
В.2. Обработка и представление результатов
многократных измерений
Допустим, что мы n раз измерили значение некоторой величины x. Вследствие случайных факторов получается совокупность n различных значений одной и той же величины x. Эта совокупность значений получила название конечной выборки. Пусть максимальное измеренное значение равно xmax, минимальное – xmin. Представим результаты измерений в графической форме. Для этого предварительно проведем некоторую их обработку. Разобьем полный интервал изменения величины x на m более мелких интервалов и введем величину интервала
Dx = (xmax – xmin)/m. Для каждого такого интервала определим количество измерений Dn, для которых значение величины x попадает в рассматриваемый интервал. Определим величину у = (Dn/n)/Dx и построим график зависимости y(x). Величина Dn/n в этом отношении определяет долю от общего числа измерений, приходящуюся на выбранный интервал. Пример возможного такого графика приведен на рис. В.1.

Рис. В .1. Гистограмма результатов измерений величины x
График представляет собой столбчатую диаграмму, которая называется гистограммой. Гистограмма достаточно наглядно демонстрирует, как распределены значения результатов измерений: одни значения величины x в процессе измерений получались довольно редко, другие – более часто, а какие-то – очень часто. На некоторый интервал Dx приходится максимальное значение величины y.
Из опыта следует, что при увеличении числа измерений гистограмма будет принимать простую и вполне определенную форму, которая для множества различных экспериментов оказывается универсальной. Если совершить предельный переход: n ® ¥, Dx ® 0, то гистограмма превратится в непрерывную кривую, которая описывает функция следующего вида:
f(x) = A exp{–(x – x0) 2/2s 2}. (В.1)
Эта зависимость получила название функции распределения Гаусса, или закона нормального распределения Гаусса. Ее график изображен на рис. В.2. Изображенная непрерывная кривая является, таким образом, предельным,или, как его еще называют, генеральным распределением.

Рис. В.2. Функция распределения Гаусса
Предельное распределение – это теоретическая идеализация, к которой никогда нельзя абсолютно точно приблизиться в эксперименте. Чем больше количество измерений, тем ближе гистограмма к предельному распределению. Теоретическая идеализация, хотя и недостижима, очень важна: она демонстрирует предельные возможности распределения результатов в данном эксперименте. Если бы могли получить в эксперименте предельное распределение, то информация, содержащаяся в нем, была максимально возможной и полной.
Следует подчеркнуть, что не все предельные распределения имеют вид нормального распределения Гаусса. Но такое распределение чаще всего будет соответствовать Вашим экспериментальным данным. По этой причине мы рассматриваем именно это распределение. Возможно, в дальнейшем Вы познакомитесь и с другими распределениями.
Нормальное (генеральное) распределение характеризуется двумя параметрами:
1) генеральным средним значением x0 ;
2) генеральным отклонениемs.
Генеральное среднее представляет собой то значение x, на которое приходится максимум функции распределения Гаусса. Значения случайной величины x распределены относительно x0 симметрично (кривая нормального распределения имеет ось симметрии, проходящую через координату x0).
Генеральное отклонение представляет собой меру ширины кривой нормального распределения. Чем меньше значение s, тем быстрее уменьшается значение функции Гаусса по мере удаления значения x от величины генерального среднего, тем уже кривая нормального распределения, меньше разброс значений измеряемой величины и, следовательно, точнее измерение.
Функция распределения Гаусса позволяет рассчитать долю из-
мерений, приходящуюся на интересующий интервал значений вели-
чины x:
 , (В.2)
, (В.2)
где x1 – нижняя граница выбранного интервала значений величины х;
x2 – верхняя граница выбранного интервала значений величины х.
Функция распределения Гаусса (В.1) удовлетворяет условию нормировки:
 .
.
Поэтому (В.2) можно интерпретировать как вероятность P того, что «истинное» значение измеряемой величины окажется в интересующем нас интервале. Из геометрического смысла интеграла следует, что площадь под кривой нормального распределения в пределах выбранного интервала (см. рис. В.2), отнесенная к полной площади под всей кривой, должна давать величину этой вероятности и, соответственно, значение Δn/n.
Используя вероятностный смысл функции Гаусса, можно показать, что среднее значение измеряемой величины, определяемое как

в случае нормального распределения совпадает с x0, т. е.  . Поэтому величина x0 и получила название среднего значения генерального (нормального) распределения,илигенерального среднего.
. Поэтому величина x0 и получила название среднего значения генерального (нормального) распределения,илигенерального среднего.
Аналогично можно показать, что значение s совпадает с величиной стандартного, илисреднеквадратичного, отклонения, квадрат которого для нормального распределения определяется выражением
(x –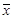 )2 f dx. Поэтому s называется среднеквадратичным (стандартным) отклонением генерального (нормального) распределения,или генеральным отклонением. Среднеквадратичноеотклонение характеризует среднюю меру разброса (отклонения) случайной величины x от среднего значения
)2 f dx. Поэтому s называется среднеквадратичным (стандартным) отклонением генерального (нормального) распределения,или генеральным отклонением. Среднеквадратичноеотклонение характеризует среднюю меру разброса (отклонения) случайной величины x от среднего значения 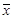 . Обратите внимание: сначала суммируются (интегрируются) значения величины (x –
. Обратите внимание: сначала суммируются (интегрируются) значения величины (x – 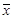 )2 – квадраты всех отклонений от среднего. Квадратный корень из этой суммы и дает величину среднеквадратичного отклонения (с определением связано название величины). Если бы суммировались сами отклонения, т. е. величины
)2 – квадраты всех отклонений от среднего. Квадратный корень из этой суммы и дает величину среднеквадратичного отклонения (с определением связано название величины). Если бы суммировались сами отклонения, т. е. величины
(x – 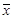 ), то в силу симметрии нормального распределения Гаусса результат был бы равен нулю. Это обусловлено тем, что отрицательные и положительные по знаку отклонения являются равновероятными. По этой причине вкачестве средней меры отклонения случайной величины от среднего используется именно среднеквадратичное отклонение.
), то в силу симметрии нормального распределения Гаусса результат был бы равен нулю. Это обусловлено тем, что отрицательные и положительные по знаку отклонения являются равновероятными. По этой причине вкачестве средней меры отклонения случайной величины от среднего используется именно среднеквадратичное отклонение.
Возьмем интервал (x0– Δx, x0+ Δx), границы которого симметричны по отношению к генеральному среднему. Пользуясь (В.2), для нормального распределения можно определить вероятность P попадания «истинного» значения измеряемой величины в этот интервал. Если вероятность определена, то интервал называется доверительным интервалом измерения, а вероятность – доверительной вероятностью, или надежностью измерения. Надежность измерения выражается или в долях единицы или в процентах и зависит от величины выбранного интервала.
Если задан доверительный интервал с указанием величины надежности (вероятности P), то информация о результатах измерения считается представленной с учетом случайных погрешностей измерения. Величина Δx, характеризующая ширину доверительного интервала, называется доверительной погрешностью.
В качестве доверительного интервала для нормального распределения чаще всего используется интервал (x0– s, x0+ s), связанный со стандартным отклонением. Величина доверительной вероятности для такого интервала составляет приблизительно 68,3 %.
Если взять Δx = 2s, то P = 95,5 %. При Δx = 3s величина P = 99,7 %. Последнее, например, означает, что вероятность обнаружить результат измерения величины x за пределами интервала (x0 – 3s, x0 + 3s) составляет всего 0,3 %. Можно считать, что «истинное» значение измеряемой величины практически находится в этом интервале.
От функции распределения Гаусса, которая является теоретической предельной идеализацией, вернемся теперь к нашему реальному распределению (см. рис. В.1), в котором количество измерений n представляет собой конечную величину. Как в этом случае определяется доверительный интервал и представляются результаты измерений?
Аналогом величины x0выступает величина выборочного среднего значения (среднеарифметического для конечной выборки)
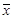 =
= 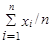 . (В.3)
. (В.3)
Аналогом величины s является величина выборочного среднеквадратичного отклонения
Sx = . (В.4)
. (В.4)
Чтобы получить оценку доверительного интервала для конечного числа измерений, приходится вводить величину tS– коэффициент Стьюдента (псевдоним английского математика В.С. Госсета). Только введение этого коэффициента позволяет найти доверительную вероятность для заданного интервала значений или определить интервал для заданной величины вероятности. Последняя из этих двух операций более простая, поэтому мы будем поступать именно так. Значения коэффициента Стьюдента для различных значений n и P даны
в табл. В.1.
Т а б л и ц а В.1
Значения коэффициента Стьюдента
Задав необходимое значение надежности измерения (вероятнос- ти P), находим по… Величину доверительной погрешности измерения находим по формулеВ.3. Приборная погрешность
Измерительные приборы вносят свой вклад в погрешность измерения, зависящий от точности прибора. Соответствующую величину принято называть приборной… Для определения приборной погрешности, связанной со случайными факторами, мы… 1. Если прибор имеет класс точности (его величина указывается в паспорте и (или) на шкале прибора), то приборная…Цель работы
В пункте формулируется цель конкретной лабораторной работы.
Таблица измерительных приборов
В таблице приводятся основные сведения об используемыхизмерительных приборах.
| На- зва- ние | Фаб- ричный номер | Сис- тема | Класс точ-ности | Предел измере-ний | Цена деле-ния | Довери-тельная погреш-ность |
Исходные данные и рабочие формулы
В пункте приводятся данные из паспорта экспериментальной установки, константы, необходимые для вычислений, и формулы, по которым будут вычисляться величины и их погрешности в данной лабораторной работе.
Электрическая схема установки
Этот пункт приводится только в том случае, если измерения связаны с электрической схемой.
Таблица измерений
В пункте приводится таблица, в которую заносятся результаты прямых и косвенных измерений.
6. Расчет
В пункте приводится по одному примеру расчета каждой величины и ее погрешности. Для этого показывается подстановка конкретных значений в рабочую формулу и записывается полученный при этом результат вычислений.
Результаты
Приводятся окончательные результаты измерений: полученное среднее значение с погрешностью, таблица результатов или график.
Вывод
В пункте приводится вывод, полученный в процессе анализа результатов эксперимента. Вывод должен касаться сравнения теоретических предсказаний с экспериментальными данными, характерных значений полученных величин и их погрешностей, возможных факторов, определяющих систематические погрешности измерений.
Литература
Приводится список литературы, использованной в процессе подготовки и при выполнении лабораторной работы.
В.7. Приложение к протоколу
Как было сказано выше, протокол является формой представления результатов лабораторных измерений с их последующей математической обработкой.
Для ряда лабораторных работ требуется до выполнения измерений получить ожидаемые теоретические результаты. Это позволяет студентам, во-первых, лучше разобраться с тем кругом физических понятий и законов, которые будут изучаться в лабораторной работе, и, следовательно, осознанно проводить опыты, и, во-вторых, сравнив ожидаемые теоретические результаты с результатами, полученными в ходе эксперимента, сделать обоснованное заключение о применимости использованной теории.
Задание по теоретическому расчету студенты выполняют в процессе подготовки к лабораторной работе. Явившись на занятие, студент обязан показать преподавателю полученные теоретические результаты вместе с заготовкой протокола. Это – необходимое условие допуска к выполнению экспериментов.
Одновременно с протоколом, содержащим результаты опытов, студент сдает теоретические результаты, оформленные как приложение к протоколу.
Обычно студенческая бригада, выполняющая лабораторную работу на одной установке, состоит из 2-3 человек. Рекомендуется каждому члену бригады присвоить один из номеров 1, 2, 3, распределив фамилии студентов по алфавиту. Каждый член бригады получает индивидуальное теоретическое задание в соответствии со своим номером, содержание которого приведено в описании лабораторной работы.
Лабораторная работа № 0
Определение объема тела
цилиндрической формы
Цель работы – на достаточно простом примере научиться проводить измерения физической величины, обрабатывать и представлять результаты прямых и косвенных измерений.
Объем цилиндра рассчитывается по формуле
V = π d2 h/4 , (*)
где d – диаметр основания и h – высота цилиндра.
Следовательно, объем тела цилиндрической формы можно определить из косвенного измерения, произведя прямые измерения диаметра и высоты.
Обработка и представление результатов
прямых измерений
Так как у реального цилиндрического тела значения d и h, измеренных в разных местах и направлениях, могут оказаться разными, то следует произвести многократные измерения диаметра и высоты для нескольких сечений цилиндра. Если результаты многократных измерений получатся разными, то следует произвести их статистическую обработку в соответствии с п. В.2. Предстоит определить средние значения d и h, среднеквадратичные отклонения Sd и Sh, доверительные погрешности Dd и Dh (доверительную вероятность следует выбирать близкую к 100 %).
В качестве измерительного прибора в данной работе Вы будете использовать линейку или штангенциркуль. Прибор позволит Вам измерить диаметр и высоту цилиндра. Приборная погрешность δ линейки и штангенциркуля определяется ценой деления. Приступая к измерениям, Вам необходимо определить цену деления измерительного прибора.
Доверительные погрешности Dd и Dh , полученные в результате статистической обработки, следует сравнить с приборной погрешностью δ. Если, например, большим оказывается значение dd , то результат многократных прямых измерений диаметра представляется в виде
d ± Dd ( n = ... , P = ... ) .
Если выполняется условие δ > Dd , то результат представляется в виде
d ± δ .
В последнем случае считается, что все имеющиеся случайные погрешности перекрываются погрешностью прибора. Именно в такой ситуации можно ограничиваться однократным измерением.
Обработка и представление результатов
косвенного измерения
Возможны два варианта обработки и представления результатов косвенного измерения объема.
I. По результатам многократных измерений d и h производятся многократные вычисления значений объема V. После этого производятся статистическая обработка и представление результатов в соответствии с п. В.2 в форме
V ± ∆V ( n = ... , P = ... ) .
II. Производится оценка среднего значения V путем подстановки средних значений d и h в формулу для вычисления объема. Оценка погрешности DV производится в соответствии с формулой (В.7), учитывающей связь погрешностей прямых и косвенных измерений. Результат представляется в форме
V ± DV .
Строго говоря, варианты в общем случае дают разные результаты как для средних значений, так и для погрешностей величин, определяемых с помощью косвенных измерений. Но если погрешности существенно меньше самих величин, то результаты оказываются достаточно близкими.
На практике чаще используется второй вариант, позволяющий сэкономить время на многократных вычислениях. А в том случае, когда прямые измерения являются однократными, это единственно возможный подход. Поэтому именно второй вариант представления результатов косвенных измерений Вам предстоит использовать в этой и в последующих лабораторных работах.
Задание к работе
1. Используя формулы (В.7) и (*), получите формулу для определения погрешности DV. Учтите, что при вычислении объема по формуле (*) число π округляется и, следовательно, характеризуется некоторой погрешностью округления.
2. Определите цену деления и приборную погрешность измерительного прибора.
3. Подготовьте протокол:
– оформите титульный лист;
– укажите цель работы в п. 1 протокола;
– начертите и заполните таблицу измерительных приборов в п. 2;
– запишите рабочие формулы в п. 3 (формула для определения средних значений величин, формула для определения среднеквадратичного отклонения, формула для определения доверительной погрешности, формула для определения объема, выведенная Вами формула для определения DV – погрешности косвенного измерения объема);
– п. 4 отсутствует;
– в п. 5 начертите две таблицы (см. табл. В.2) для обработки результатов многократных (n = 5) измерений диаметра и высоты цилиндра.
4. Произведите пятикратные измерения диаметра и высоты цилиндра в разных сечениях тела. Результаты измерений занесите в таблицы.
5. Произведите статистическую обработку результатов измерений. Определите средние значения диаметра и высоты, а также соответствующие им доверительные погрешности. Сравните доверительные погрешности с приборной погрешностью измерительного прибора.
6. Приведите оценку среднего значение объема цилиндра и соответствующей ему погрешности.
7. В п. 6 протокола продемонстрируйте, как проводились расчеты средних величин и их погрешностей.
8. В п. 7 протокола приведите окончательные результаты прямых и косвенных измерений в стандартной форме.
9. Проанализируйте полученные результаты, сделайте вывод и запишите его в п. 8 протокола.
Список литературы
1. Агекян Т.А. Основы теории ошибок для астрономов и физиков. – М: Наука, 1972.
2. Кассандрова О.Н., Лебедев В.В. Обработка результатов измерений. – М: Наука, 1970.
3. Сквайрс Дж. Практическая физика / Пер. с англ. – М.: Мир,
1971.
4. Тейлор Дж. Введение в теорию ошибок / Пер. с англ. – М.: Мир, 1985.
5. Худсон Д. Статистика для физиков / Пер. с англ. – М.: Мир, 1967.
Лабораторная работа № 1
Измерение скорости пули
с помощью баллистического маятника
Цель работы – с помощью баллистического маятника определить скорость пуль с различными массами. Рабочую формулу для экспериментального определения скорости пули и теоретическую зависимость скорости пули от ее массы получить исходя из законов сохранения импульса и энергии.
Описание установки
Баллистический маятник представляет собой массивный цилиндр М, заполненный пластилином. В цилиндр в горизонтальном направлении производят выстрел пулей массы 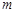 из пружинного пистолета Р, неподвижно закрепленного вблизи маятника (рис. 1.1). Пуля проникает в пластилин, застревает в нем и дальше продолжает двигаться вместе с маятником (абсолютно неупругий удар). Маятник закреплен так, чтобы в процессе отклонения он совершал поступательное движение. Максимальное отклонение маятника от его положения равновесия фиксируется механизмом N.
из пружинного пистолета Р, неподвижно закрепленного вблизи маятника (рис. 1.1). Пуля проникает в пластилин, застревает в нем и дальше продолжает двигаться вместе с маятником (абсолютно неупругий удар). Маятник закреплен так, чтобы в процессе отклонения он совершал поступательное движение. Максимальное отклонение маятника от его положения равновесия фиксируется механизмом N.

Рис. 1.1
Методика эксперимента, вывод формул
1. Вывод формулы зависимости скорости пули от ее массы. Выбрав пулю массы  , зарядим пистолет, сжав его пружину. При этом
, зарядим пистолет, сжав его пружину. При этом
в пружине будет запасена потенциальная энергия
 , (1.1)
, (1.1)
где 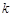 – коэффициент упругости пружины,
– коэффициент упругости пружины,  – деформация пружины.
– деформация пружины.
Предположим, что вся энергия сжатой пружины при выстреле полностью превращается в кинетическую энергию пули. Это означает, что мы пренебрегаем потерями энергии на преодоление трения между пулей и стволом пистолета и на сообщение кинетической энергии самой пружине. Учтем, кроме того, что геометрические размеры всех пуль одинаковы, а значит, одинакова деформация пружины для любой пули и, следовательно, одинакова запасаемая пружиной потенциальная энергия. Тогда из закона сохранения механической энергии следует, что пули различных масс 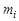 , вылетая из пружинного пистолета, должны иметь одинаковые кинетические энергии
, вылетая из пружинного пистолета, должны иметь одинаковые кинетические энергии
 , (1.2)
, (1.2)
где 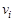 – скорость i-й пули после выстрела.
– скорость i-й пули после выстрела.
Из (1.2) получаем зависимость скорости пули после выстрела от ее массы
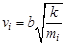 . (1.3)
. (1.3)
Поскольку величины  и
и 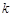 для всех пуль одинаковы, то график ожидаемой зависимости скорости пули
для всех пуль одинаковы, то график ожидаемой зависимости скорости пули 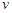 от
от  должен согласно формуле (1.3) представлять собой прямую линию, проходящую через начало координат.
должен согласно формуле (1.3) представлять собой прямую линию, проходящую через начало координат.
2. Вывод рабочей формулы. Пролетев небольшое расстояние между пистолетом и маятником, пуля входит в пластилин, заполняющий цилиндр, и за счет вязкого трения быстро теряет скорость. При этом часть механической энергии пули расходуется на неупругую деформацию и превращается во внутреннюю энергию пластилина и пули, т. е. пластилин и пуля нагреваются. Такой удар пули и маятника, в результате которого они начинают двигаться как единое целое, называется абсолютно неупругим. Механическая энергия в процессе такого удара не сохраняется (убывает).
Процесс удара – кратковременный. Если масса маятника достаточно велика по сравнению с массой пули ( ), то за время удара он в силу своей инерционности не успевает выйти из положения равновесия. Это позволяет считать систему маятник–пуля в момент удара замкнутой в горизонтальном направлении, так как сила тяжести и сила натяжения подвеса направлены вертикально при вертикальном положении маятника. Для замкнутой системы можно применить закон сохранения импульса
), то за время удара он в силу своей инерционности не успевает выйти из положения равновесия. Это позволяет считать систему маятник–пуля в момент удара замкнутой в горизонтальном направлении, так как сила тяжести и сила натяжения подвеса направлены вертикально при вертикальном положении маятника. Для замкнутой системы можно применить закон сохранения импульса
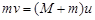 , (1.4)
, (1.4)
где 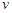 – скорость пули до удара (при этом скорость маятника равна нулю);
– скорость пули до удара (при этом скорость маятника равна нулю);  – скорость, приобретенная системой маятник–пуля сразу после удара.
– скорость, приобретенная системой маятник–пуля сразу после удара.
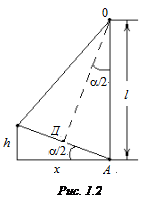 Маятник вместе с пулей, получив за счет неупругого удара импульс, отклоняется от положения равновесия на угол
Маятник вместе с пулей, получив за счет неупругого удара импульс, отклоняется от положения равновесия на угол 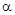 . В процессе отклонения на маятник действуют сила тяжести (вниз) и сила упругости подвеса (перпендикулярно направлению мгновенной скорости маятника). Если пренебречь потерями энергии на трение в подвесе и на сопротивление воздуха, то работу при отклонении маятника совершает только гравитационная сила. Это позволяет воспользоваться законом сохранения механической энергии
. В процессе отклонения на маятник действуют сила тяжести (вниз) и сила упругости подвеса (перпендикулярно направлению мгновенной скорости маятника). Если пренебречь потерями энергии на трение в подвесе и на сопротивление воздуха, то работу при отклонении маятника совершает только гравитационная сила. Это позволяет воспользоваться законом сохранения механической энергии
 , (1.5)
, (1.5)
где  – наибольшая высота, на которую поднимается маятник (рис. 1.2). Слева в формуле (1.5) стоит кинетическая энергия при поступательном движении маятника сразу после удара (в этой точке потенциальную энергию принимаем равной нулю), а справа – потенциальная энергия системы в момент ее остановки на высоте
– наибольшая высота, на которую поднимается маятник (рис. 1.2). Слева в формуле (1.5) стоит кинетическая энергия при поступательном движении маятника сразу после удара (в этой точке потенциальную энергию принимаем равной нулю), а справа – потенциальная энергия системы в момент ее остановки на высоте 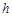 .
.
Выразим высоту 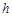 через соответствующее горизонтальное смещение маятника
через соответствующее горизонтальное смещение маятника 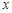 , которое удобнее измерять. Предположим, что угол отклонения маятника от положения равновесия
, которое удобнее измерять. Предположим, что угол отклонения маятника от положения равновесия 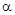 мал. Из рис. 1.2 видно, что
мал. Из рис. 1.2 видно, что
 , (1.6)
, (1.6)
где  – длина нити подвеса.
– длина нити подвеса.
Из (1.6) получаем
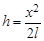 . (1.7)
. (1.7)
Уравнения (1.4), (1.5) и (1.7) образуют систему, решая которую получим скорость пули 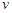 перед ударом
перед ударом
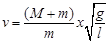 . (1.8)
. (1.8)
По выражению (1.8), осуществив прямые измерения смещения маятника 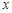 и зная значения остальных величин, входящих в эту рабочую формулу, определим скорость пули
и зная значения остальных величин, входящих в эту рабочую формулу, определим скорость пули 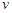 путем косвенных измерений. Измерив скорости
путем косвенных измерений. Измерив скорости 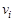 для пуль с разными массами
для пуль с разными массами  можно, следовательно, убедиться в справедливости теоретической зависимости (1.3).
можно, следовательно, убедиться в справедливости теоретической зависимости (1.3).
3. Вывод формулы для определения погрешности косвенных измерений скорости 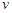 . Методика оценки истинных значений и погрешности при прямых и косвенных измерениях изложена в [1].
. Методика оценки истинных значений и погрешности при прямых и косвенных измерениях изложена в [1].
Проведя прямые многократные измерения смещения маятника 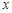 для одной и той же пули (см. задание к работе) можно (см. [1]) оценить истинное значение
для одной и той же пули (см. задание к работе) можно (см. [1]) оценить истинное значение 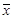 и доверительную погрешность
и доверительную погрешность 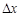 этой величины, записав результат в виде
этой величины, записав результат в виде 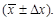 Истинные значения остальных аргументов рабочей формулы (1.8) и их доверительные погрешности определены заранее и указаны в таблице исходных данных, помещенной около установки, и в Приложении. Подставляя истинные значения аргументов в рабочую формулу (1.8), получаем оценку истинного значения скорости пули
Истинные значения остальных аргументов рабочей формулы (1.8) и их доверительные погрешности определены заранее и указаны в таблице исходных данных, помещенной около установки, и в Приложении. Подставляя истинные значения аргументов в рабочую формулу (1.8), получаем оценку истинного значения скорости пули
 , (1.9)
, (1.9)
где черта означает оценку истинного значения.
Теперь (см. [1]) можно оценить доверительную абсолютную погрешность этой величины. В формуле (1.8) пять аргументов (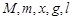 ), каждый из которых определен с некоторой погрешностью. Следовательно, формула для определения абсолютной погрешности скорости пули имеет вид
), каждый из которых определен с некоторой погрешностью. Следовательно, формула для определения абсолютной погрешности скорости пули имеет вид
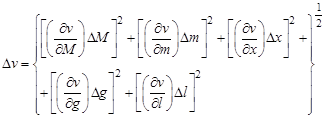 . (1.10)
. (1.10)
Пользуясь формулой (1.8), вычислим частные производные от скорости по каждому из аргументов. В результате получим следующее выражение
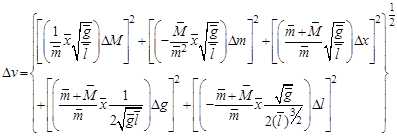 . (1.11)
. (1.11)
В формулу (1.11) входит пять квадратичных членов, каждый из которых определяет вклад погрешности одного из пяти аргументов формулы (1.8) в погрешность величины  . Прежде чем применять формулу (1.11), следует отдельно вычислить (приближенно) каждый из пяти квадратичных членов, чтобы сравнить их друг с другом. Сравнение покажет, точность определения каких аргументов мало влияет на абсолютную погрешность скорости. Эти члены из формулы (1.11) надо исключить, и только после этого, применив (1.11), получить оценку погрешности скорости
. Прежде чем применять формулу (1.11), следует отдельно вычислить (приближенно) каждый из пяти квадратичных членов, чтобы сравнить их друг с другом. Сравнение покажет, точность определения каких аргументов мало влияет на абсолютную погрешность скорости. Эти члены из формулы (1.11) надо исключить, и только после этого, применив (1.11), получить оценку погрешности скорости 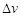 . Численные результаты, полученные с помощью формул (1.9) и (1.11), записываются в виде
. Численные результаты, полученные с помощью формул (1.9) и (1.11), записываются в виде
 м/с. (1.12)
м/с. (1.12)
Задание к работе
1. Сделайте заготовку протокола к лабораторной работе.
2. Получите допуск к выполнению лабораторной работы у преподавателя.
3. Соблюдая правила техники безопасности, зарядите пружинный пистолет пулей с наибольшей массой.
4. Подготовьте устройство  к измерению горизонтального смещения маятника. Запишите численное значение начальной координаты
к измерению горизонтального смещения маятника. Запишите численное значение начальной координаты 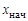 маятника по линейке отсчетного устройства
маятника по линейке отсчетного устройства  .
.
5. Осуществите первый выстрел пулей с наибольшей массой, нажав спусковую кнопку пистолета. Запишите численное значение конечной координаты  , определив его по линейке отсчетного устройства
, определив его по линейке отсчетного устройства  . Вычислите смещение маятника при первом опыте:
. Вычислите смещение маятника при первом опыте:
 .
.
Запишите величину 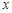 в таблицу измерений.
в таблицу измерений.
6. Проведите опыт с той же пулей пять раз, чтобы в дальнейшем провести статистическую обработку этих прямых измерений.
7. Проведите однократные измерения смещения маятника для пуль с другой массой (п. 3–5).
8. Проведите статистическую обработку прямых многократных измерений смещения маятника для первой пули согласно методике, описанной в [1]. Результаты внесите в таблицу измерений.
9. По формуле (1.9) получите оценку истинного значения скорости пули  , для которой были проведены многократные измерения. Результат внесите в таблицу измерений. Рекомендуется для получения скорости пули использовать результаты индивидуального задания для членов бригады, выполняющих лабораторную работу на одной установке.
, для которой были проведены многократные измерения. Результат внесите в таблицу измерений. Рекомендуется для получения скорости пули использовать результаты индивидуального задания для членов бригады, выполняющих лабораторную работу на одной установке.
10. Получите оценку абсолютной погрешности косвенных измерений скорости этой пули (формула (1.11)). Прежде чем применять формулу (1.11), следует отдельно вычислить (приближенно) каждый из пяти квадратичных членов, чтобы сравнить их друг с другом. Сравнение покажет, от каких аргументов сильнее всего зависит величина погрешности 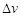 , а какие члены формулы (1.11) можно не учитывать. Результат внесите в таблицу измерений.
, а какие члены формулы (1.11) можно не учитывать. Результат внесите в таблицу измерений.
11. Вычислите скорости пуль с другой массой (формула (1.9)). Погрешность для этих однократно проведенных опытов оценивать не надо. При этом также (см. п. 9) рекомендуется использовать результаты индивидуального задания.
12. Учитывая, что для проведенных опытов должна выполняться зависимость (1.3), постройте оси графика этой зависимости в координатах  для диапазона численных значений, соответствующего используемым в опытах массам пуль и полученным для них скоростям.
для диапазона численных значений, соответствующего используемым в опытах массам пуль и полученным для них скоростям.
13. Нанесите на этот график точки, соответствующие полученным в опытах значениям скорости для каждой пули. Учитывайте, лежат ли экспериментальные точки на одной прямой.
14. Укажите на этом графике для каждой экспериментальной точки диапазон, внутри которого лежит истинное значение скорости, то есть графически укажите найденную погрешность. При этом считайте, что погрешность, найденная для скорости только одной пули, является такой же для скоростей остальных пуль.
15. Сделайте выводы.
Контрольные вопросы
1. Сформулируйте цель данной лабораторной работы.
2. Какой закон сохранения позволяет получить зависимость скорости пули, выпущенной из пружинного пистолета, от ее массы? Какие предположения при этом делаются?
3. Выполняется ли закон сохранения механической энергии системы маятник–пуля при ударе?
4. В какой момент опыта выполняется закон сохранения импульса для системы маятник–пуля?
5. Начиная с какого момента опыта можно использовать закон сохранения механической энергии для системы маятник–пуля?
6. Как рассчитать долю кинетической энергии пули, которая расходуется на неупругую деформацию при ударе?
7. Запишите систему уравнений для получения скорости пули через горизонтальное смещение маятника после удара. Решив систему, получите рабочую формулу.
8. Где при выводе рабочей формулы используется тот факт, что маятник движется поступательно?
9. Как изменится смещение маятника, если изменить его массу?
10. Как изменится смещение маятника, если изменить длину подвеса?
11. Какие величины в опыте определяются путем прямых, а какие путем косвенных измерений?
12. Как оценить истинные значения при прямых и как – при косвенных измерениях?
13. Как оценить доверительную погрешность при прямых и как – при косвенных измерениях? Какой смысл этой погрешности, почему результат измерений записывают в виде  ?
?
14. Какой смысл, строить график зависимости скорости пули от ее массы в координатах  ?
?
Индивидуальные задания для членов бригады,
выполняющих лабораторную работу на одной установке
| Номер члена бригады | Индивидуальное задание |
| Постройте график зависимости скорости пули v перед ударом от горизонтального смещения маятника x для пули массой m1 (формула (1.8)). Рекомендуемый диапазон изменения величины x от 0 до 10 см. Численные значения массы маятника M, массы пули m1, длины подвеса l возьмите в таблице исходных данных, помещенной в Приложении или около лабораторной установки, на которой Вам предстоит выполнять опыты | |
| Выполните задание, аналогичное заданию для первого номера, но для пули массой m2 | |
| Выполните задание, аналогичное заданию для первого номера, но для пули массой m3 |
Литература
Введение к настоящим методическим указаниям.
Лабораторная работа № 3
Определение момента инерции
маятника Обербека
Цели работы:1) определить экспериментальным путем момент инерции маятника с учетом действия тормозящего момента сил сопротивления; 2) исследовать экспериментальную зависимость момента инерции маятника от расстояния грузов, закрепленных на стержнях маятника, до оси вращения и сравнить с теоретической зависимостью; 3) рассчитать момент инерции маятника Обербека на основе уравнения динамики поступательного движения груза, прикрепленного к нити, наматываемой на шкив маятника, и уравнения вращательного движения маятника.
Описание установки
 Маятник Обербека представляет собой крестовину, состоящую из четырех стержней с нанесенными на них делениями, прикрепленных к барабану с осью (рис. 3.1). На стержни надеваются одинаковые грузы массой
Маятник Обербека представляет собой крестовину, состоящую из четырех стержней с нанесенными на них делениями, прикрепленных к барабану с осью (рис. 3.1). На стержни надеваются одинаковые грузы массой  , которые могут быть закреплены на расстоянии
, которые могут быть закреплены на расстоянии  от оси вращения. На барабане имеется два шкива с различными диаметрами
от оси вращения. На барабане имеется два шкива с различными диаметрами 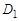 и
и  . На шкив наматывается нить, к свободному концу которой прикрепляется груз массой
. На шкив наматывается нить, к свободному концу которой прикрепляется груз массой 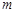 . Под действием груза нить разматывается и приводит маятник во вращательное движение, которое предполагается равноускоренным. Время движения груза
. Под действием груза нить разматывается и приводит маятник во вращательное движение, которое предполагается равноускоренным. Время движения груза  измеряется электронным секундомером, включение которого производится кнопкой «Пуск», а остановка происходит по сигналу фотодатчика. Груз опускается на расстояние x, измеряемое вертикально закрепленной линейкой. Установка имеет электромеханическое тормозное устройство, управление которым осуществляется по сигналу фотодатчика.
измеряется электронным секундомером, включение которого производится кнопкой «Пуск», а остановка происходит по сигналу фотодатчика. Груз опускается на расстояние x, измеряемое вертикально закрепленной линейкой. Установка имеет электромеханическое тормозное устройство, управление которым осуществляется по сигналу фотодатчика.
Расчет момента инерции маятника Обербека
и момента сил сопротивления
Для расчета движения механической системы маятник–груз применим уравнение динамики поступательного движения для груза, закрепленного на нити, и уравнение динамики вращательного движения для маятника.
Груз массой 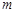 движется с ускорением
движется с ускорением 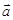 под действием результирующей сил тяжести
под действием результирующей сил тяжести 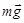 и силы натяжения нити
и силы натяжения нити  (рис. 3.2). Запишем для груза второй закон Ньютона в проекции на направление движения
(рис. 3.2). Запишем для груза второй закон Ньютона в проекции на направление движения
 (3.1)
(3.1)
 Сила натяжения передается нитью от груза к шкиву вращающегося маятника. Если предположить, что нить невесомая, то на шкив маятника действует сила
Сила натяжения передается нитью от груза к шкиву вращающегося маятника. Если предположить, что нить невесомая, то на шкив маятника действует сила 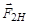 , равная по величине
, равная по величине  и противоположная ей по направлению (следствие третьего закона Ньютона:
и противоположная ей по направлению (следствие третьего закона Ньютона:  ). Сила натяжения создает вращательный момент
). Сила натяжения создает вращательный момент 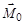 относительно горизонтальной оси O, направленный вдоль этой оси «от нас» и приводящий в движение маятник Обербека. Величина этого момента равна
относительно горизонтальной оси O, направленный вдоль этой оси «от нас» и приводящий в движение маятник Обербека. Величина этого момента равна  , где
, где 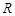 – радиус шкива, на который намотана нить,
– радиус шкива, на который намотана нить,  , где
, где  – диаметр шкива.
– диаметр шкива.
Момент силы сопротивления относительно оси вращения  направлен «к нам», т. е. в противоположную по отношению к вращательному моменту сторону.
направлен «к нам», т. е. в противоположную по отношению к вращательному моменту сторону.
Запишем для маятника основной закон динамики вращательного движения
 ,
,
где  – результирующий момент сил;
– результирующий момент сил; 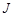 – момент инерции маятника;
– момент инерции маятника; 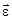 – угловое ускорение.
– угловое ускорение.
В скалярной форме это уравнение имеет вид (записаны проекции векторов моментов сил и углового ускорения на ось вращения О,направление которой выбрано «от нас»)
 . (3.2)
. (3.2)
Используя кинематическую связь линейного и углового ускоре-
ния 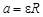 , а также уравнение движения груза при нулевой начальной
, а также уравнение движения груза при нулевой начальной
скорости 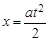 , выразим
, выразим 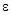 через измеряемые величины
через измеряемые величины 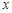 и
и 
 . (3.3)
. (3.3)
Решим систему уравнений (3.1) и (3.2), для чего умножим (3.1) на 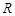 и прибавим к (3.2)
и прибавим к (3.2)
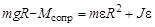 .
.
Выражаем момент инерции маятника Обербека
 . (3.4)
. (3.4)
Все величины, кроме 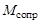 , входящие в это уравнение, известны. Поставим задачу экспериментального определения
, входящие в это уравнение, известны. Поставим задачу экспериментального определения 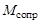 .
.
Пусть J – момент инерции маятника Обербека без грузов. Из (3.4) следует, что
 . (3.5)
. (3.5)
В условиях эксперимента 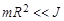 , что позволяет считать зависимость e(m) линейной.
, что позволяет считать зависимость e(m) линейной.
Эту зависимость можно использовать для экспериментальной оценки величины 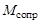 . Действительно, если полученную экспериментально зависимость
. Действительно, если полученную экспериментально зависимость  экстраполировать до пересечения с осью абсцисс, т. е. до точки
экстраполировать до пересечения с осью абсцисс, т. е. до точки  на этой оси, для которой выполняется (см. 3.5) равенство
на этой оси, для которой выполняется (см. 3.5) равенство  , то это позволит определить
, то это позволит определить 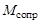 как
как
 . (3.6)
. (3.6)
Для определения момента инерции маятника J воспользуемся (3.4), где величина 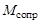 предварительно определена из измерений e(m) и формулы (3.6). Подставив выражение e из (3.3) и
предварительно определена из измерений e(m) и формулы (3.6). Подставив выражение e из (3.3) и 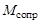 из (3.6) в (3.4), получим рабочую формулу для определения момента инерции маятника
из (3.6) в (3.4), получим рабочую формулу для определения момента инерции маятника
 .
.
Для используемого в работе маятника Обербека справедливо неравенство  . Учитывая это, получаем
. Учитывая это, получаем
 .
.
Для расчетов удобно представить момент инерции в виде
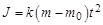 , (3.7)
, (3.7)
где 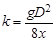 .
.
Для определения момента инерции маятника необходимо измерить время  опускания груза массой
опускания груза массой 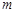 на расстояние
на расстояние 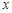 .
.
Зависимость момента инерции маятника
от расстояния грузов до оси вращения
Момент инерции маятника Обербека может быть представлен как сумма моментов инерции барабана со стержнями ( ) и моментов инерции четырех грузов массой
) и моментов инерции четырех грузов массой  , закрепленных на расстояниях r от оси вращения (
, закрепленных на расстояниях r от оси вращения ( ). Если размеры этих грузиков малы по сравнению с
). Если размеры этих грузиков малы по сравнению с  , то их можно считать материальными точками. Для материальной точки момент инерции равен
, то их можно считать материальными точками. Для материальной точки момент инерции равен 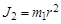 . Тогда момент инерции маятника
. Тогда момент инерции маятника
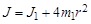 . (3.8)
. (3.8)
Эту зависимость момента инерции от расстояния грузов до оси вращения предполагается проверить, используя результаты опытов, полученные по формуле (3.7).
Значение  можно взять из данных эксперимента для определения момента инерции маятника Обербека без грузов, считая, что момент сил сопротивления остается постоянным.
можно взять из данных эксперимента для определения момента инерции маятника Обербека без грузов, считая, что момент сил сопротивления остается постоянным.
Задание к работе
1. Приступив к работе, снимите грузы  со стержней, если они там находятся.
со стержней, если они там находятся.
2. Заранее выберите отметку (например, от 30 до 50 см), от которой начнется движение груза  .
.
3. Вращая маятник рукой, намотайте нить на шкив большего диаметра. Следите, чтобы груз  достиг выбранного положения.
достиг выбранного положения.
4. Включите электронный секундомер.
5. Проведите первый опыт, используя в качестве груза, тянущего нить, только одну подставку массой  без подгрузков. Предварительно нажатием кнопки «Режим» установите режим №1 (светится индикатор «Реж.1»). Затем нажмите кнопку «Пуск». При этом отключится тормозное устройство, удерживающее маятник, и одновременно включится секундомер. При включенном режиме №1 секундомер в момент прохождения грузом нижней точки автоматически остановится, причем одновременно сработает тормозное устройство. Внесите результаты первого опыта в таблицу измерений.
без подгрузков. Предварительно нажатием кнопки «Режим» установите режим №1 (светится индикатор «Реж.1»). Затем нажмите кнопку «Пуск». При этом отключится тормозное устройство, удерживающее маятник, и одновременно включится секундомер. При включенном режиме №1 секундомер в момент прохождения грузом нижней точки автоматически остановится, причем одновременно сработает тормозное устройство. Внесите результаты первого опыта в таблицу измерений.
6. Проведите по одному опыту, поместив на подставку сначала один, а затем сразу два подгрузка. Результаты внесите в таблицу измерений. По формуле (3.3) рассчитайте величину углового ускорения 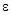 для соответствующих значений
для соответствующих значений 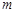 .
.
7. Постройте зависимость e(m). Определите из графика по точке его пересечения с осью абсцисс значение m0, при котором e = 0. Рассчитайте по формуле (3.6) величину момента сил сопротивления 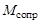 .
.
8. Проведите прямые пятикратные измерения времени опускания груза для заданного расстояния x.
9. Рассчитайте среднее время t и определите доверительную по-грешность измерения  при доверительной вероятности Р = 90 %,
при доверительной вероятности Р = 90 %,
n = 5 (см. Введение).
10. Вычислите по формуле (3.7) среднее значение момента инерции барабана со стержнями 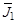 .
.
11. Определите доверительную погрешность косвенных измерений этого момента инерции  (см. Введение) и запишите результаты в виде
(см. Введение) и запишите результаты в виде 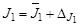 .
.
12. Закрепив грузы m1 на стержнях маятника на равном расстоянии r от оси вращения, определите это расстояние, учитывая деления, нанесенные на стержни, и указанные около установки и в Приложении исходные данные.
13. Проведите однократные измерения времени  опускания груза массой m (выберите одно значение) для одной высоты падения при трех различных расстояниях r от оси вращения.
опускания груза массой m (выберите одно значение) для одной высоты падения при трех различных расстояниях r от оси вращения.
14. Вычислите моменты инерции маятника с грузами на стержнях по формуле (3.7) при различных расстояниях r. При этом, как показали предварительные опыты, можно с допустимой точностью использовать в качестве величины m0 ее значение, найденное ранее для крестовины без грузов на спицах. Сравните полученные данные со значениями момента инерции, вычисленными по формуле (3.8) для соответствующих значений r. Результаты вычислений занесите в таблицу измерений.
15. Постройте на одном рисунке графики экспериментально полученной и теоретически ожидаемой зависимости момента инерции маятника от 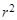 . Нанесите на график точки, соответствующие результатам, полученным при выполнении индивидуальных заданий. Проанализируйте возможные причины их несовпадения.
. Нанесите на график точки, соответствующие результатам, полученным при выполнении индивидуальных заданий. Проанализируйте возможные причины их несовпадения.
Контрольные вопросы
1. Какова цель данной работы?
2. Что такое момент инерции? Каков его физический смысл.
3. Как можно изменить момент инерции маятника Обербека?
4. Как из уравнений динамики поступательного и вращательного движений вывести рабочую формулу (3.7)?
5. В каком случае движение маятника является равноускоренным?
6. Как измерить расстояние от оси вращения до центров грузиков, закрепленных на стержнях?
7. Каким образом в данной работе подтверждается линейная за-
висимость момента инерции от квадрата расстояния тел до оси вра-
щения?
Индивидуальные задания для членов бригады,
выполняющих лабораторную работу на одной установке
| Номер члена бригады | Индивидуальное задание |
| Рассчитайте момент инерции маятника Обербека, состоящего из барабана и четырех спиц (без грузов, закрепленных на спицах). Численные значения масс и размеры барабана и спиц возьмите в таблице исходных данных, помещенной в Приложении или лабораторной установки, на которой Вам предстоит выполнять опыты | |
| Рассчитайте момент инерции маятника Обербека с грузами, закрепленными на одинаковых расстояниях на всех четырех спицах. Расстояние от поверхности барабана до грузов, за- крепленных на спицах, возьмите максимально возможным (грузы – на самом конце спиц). Численные значения масс и размеров барабана, спиц и грузов возьмите в таблице исходных данных, помещенной в Приложении или около лабораторной установки, на которой Вам предстоит выполнять опыты | |
| Выполните задание аналогичное заданию для второго номе- ра, но расстояние от поверхности барабана до грузов, закре-пленных на спицах, возьмите равным половине длины спи- цы (грузы – на середине спиц) |
Литература
Савельев И.В. Курс общей физики. – М.: Наука, 1982. – Т. 1 (и последующие издания этого курса).
Лабораторная работа № 4
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛА
Цели работы: 1) оценить момент тормозящей силы, действующий на тело в процессе вращения; 2) определить момент инерции тела с учетом момента тормозящей силы; 3) произвести расчет моментов, пользуясь энергетическими соотношениями.
Описание установки
Установка представляет собой тело со шкивом радиусом r, которое вращается в шарикоподшипниках. На шкив намотана нить, один конец которой прикреплен к шкиву, а другой – к подставке массой 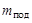 . На подставку могут помещаться подгрузки массой
. На подставку могут помещаться подгрузки массой 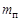 . Груз под действием силы тяжести может опускаться, приводя во вращение тело. После того как груз от отметки h0 опустится на полную длину нити до отметки h1
. Груз под действием силы тяжести может опускаться, приводя во вращение тело. После того как груз от отметки h0 опустится на полную длину нити до отметки h1
(рис. 4.1), тело, вращаясь по инерции, поднимет груз снова на некоторую высоту до отметки h2.

Рис. 4.1
В процессе движения часть механической энергии системы тело–груз расходуется на работу против тормозящей силы и, следовательно, превращается во внутреннюю энергию системы и окружающего воздуха, которые нагреваются. Из этого следует, что тело поднимет груз на высоту, меньшую начальной, т. е. отметка h2 всегда будет расположена ниже отметки h0. Тормозящая сила складывается из силы трения в подшипниках и из силы трения о воздух при движении тела и груза.
Вывод формулы для косвенных измерений момента
Тормозящей силы
Для оценки момента тормозящей силы воспользуемся энергетическими соотношениями. Поскольку силы трения являются диссипативными, то работа тормозящей… , (4.1)Вывод формулы для косвенных измерений
Момента инерции тела с учетом момента тормозящей силы
Рассмотрим систему тело–груз в начальный момент времени, когда груз находится на отметке , а в качестве конечного выберем тот момент времени, когда… Для выбранных начального и конечного состояний получимПолучение формул для определения погрешностей
Косвенных измерений момента тормозящей силы
И момента инерции тела
Методика получения оценок истинных значений величин и погрешностей при прямых и косвенных измерениях описана в [1]. При выполнении данной… Выполнив прямые многократные измерения величин и (см. задание к работе) и… Подставляя в рабочую формулу (4.6) истинные значения всех аргументов, получаем оценку истинного значения момента…Задание к работе
1. Заготовьте таблицу для прямых пятикратных измерений длины 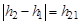 и времени
и времени 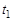 с последующей статистической обработкой полученных результатов.
с последующей статистической обработкой полученных результатов.
2. Заранее выберите отметку  от которой начнется движение груза
от которой начнется движение груза 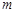 (рекомендуемое значение 50 см).
(рекомендуемое значение 50 см).
3. Вращая тело рукой, размотайте нить на полную длину и заранее определите численное значение отметки  . Обычно можно считать
. Обычно можно считать 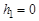 . Внесите длину
. Внесите длину 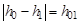 в таблицу. Оцените погрешность измерения этой длины как систематическую погрешность измерительной линейки.
в таблицу. Оцените погрешность измерения этой длины как систематическую погрешность измерительной линейки.
4. Включите электронный секундомер.
5. Вращая тело рукой, намотайте нить на шкив так, чтобы груз занял положение, соответствующее выбранной Вами начальной отметке 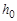 .
.
6. Проведите первый опыт, используя в качестве груза, тянущего нить, только одну подставку массой 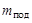 без подгрузков. Предварительно нажатием кнопки «Режим» установите режим №2 (светится индикатор «Реж.2»). Затем нажмите кнопку «Пуск». При этом отключится тормозное устройство, удерживающее тело, и одновременно включится секундомер. При включенном режиме №2 секундомер в момент прохождения грузом отметки
без подгрузков. Предварительно нажатием кнопки «Режим» установите режим №2 (светится индикатор «Реж.2»). Затем нажмите кнопку «Пуск». При этом отключится тормозное устройство, удерживающее тело, и одновременно включится секундомер. При включенном режиме №2 секундомер в момент прохождения грузом отметки  автоматически остановится, но тор-мозная система при этом не остановит движения, позволив грузу подняться до отметки
автоматически остановится, но тор-мозная система при этом не остановит движения, позволив грузу подняться до отметки 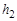 . Дождитесь момента, когда груз поднимется до отметки
. Дождитесь момента, когда груз поднимется до отметки 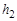 , и зафиксируйте ее численное значение. Внесите результаты первого опыта в таблицу измерений (ими будут
, и зафиксируйте ее численное значение. Внесите результаты первого опыта в таблицу измерений (ими будут 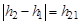 и
и 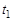 ).
).
7. Пятикратно повторите этот опыт, не меняя массу груза, что необходимо для определения случайной погрешности прямых измерений.
8. Проведите по одному опыту, поместив на подставку сначала один, а затем сразу два подгрузка. Результаты внесите в таблицу измерений.
9. Проведите статистическую обработку пятикратно проведенных прямых измерений величин 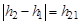 и
и 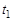 (п. 6,7), пользуясь методикой, изложенной в [1]. Получите оценку истинных значений и доверительных погрешностей для этих величин. Результаты вычислений внесите в таблицу.
(п. 6,7), пользуясь методикой, изложенной в [1]. Получите оценку истинных значений и доверительных погрешностей для этих величин. Результаты вычислений внесите в таблицу.
10. Проведите оценку истинного значения момента тормозящей силы  , пользуясь формулой (4.13).
, пользуясь формулой (4.13).
11. Проведите численную оценку квадратичных членов формулы (4.14) и, отбросив малые, оцените погрешность косвенных измерений момента тормозящей силы 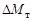 .
.
12. Проведите оценку истинного значения момента инерции тела 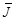 , пользуясь формулой (4.15).
, пользуясь формулой (4.15).
13. Проведите численную оценку квадратичных членов формулы (4.16) и, отбросив малые, оцените погрешность косвенных измерений момента инерции тела  .
.
14. С помощью формулы (4.6) или (4.13) проведите расчет моментов тормозящей силы для однократных опытов с другими грузами
(см. п. 8). Погрешности измерений для этих опытов вычислять не надо. Обратите внимание на закономерное изменение момента тормозящей силы с ростом массы груза.
15. С помощью формулы (4.12) или (4.15) проведите расчет момента инерции тела для однократных опытов с другими грузами (см. п. 8). Погрешности измерений для этих опытов вычислять не надо. Наблюдается ли закономерное изменение момента инерции с ростом массы груза?
Контрольные вопросы
1. Какая часть системы совершает в процессе опыта поступательное, а какая – вращательное движение?
2. Почему для описания вращательного движения удобней пользоваться угловыми кинематическими характеристиками, а для поступательного – линейными?
3. Что такое момент силы? Какие силы и моменты сил действуют на тело во время его движения?
4. Какие силы создают момент тормозящей силы? Можно ли указать точку приложения этих сил?
5. Как определить работу момента силы?
6. Сохраняется ли механическая энергия системы тело–груз в процессе опыта?
7. Как можно оценить момент тормозящей силы, пользуясь энергетическими соотношениями? Какие упрощающие предположения при этом делаются?
8. Изменяется ли момент тормозящей силы при увеличении массы груза, как и почему?
9. Что такое момент инерции тела, какое свойство тела он характеризует?
10. Как найти кинетическую энергию при поступательном и при вращательном движении?
11. Как можно определить момент инерции тела, пользуясь энергетическими соотношениями.
12. Зависит ли момент инерции тела от массы груза, закрепленного на конце нити?
13. Выведите формулу кинетической энергии тела, совершающего вращательное движение вокруг неподвижной оси.
14. Выведите рабочую формулу для оценки момента тормозящей силы.
15. Выведите рабочую формулу для момента инерции тела с учетом и без учета момента тормозящей силы. Примените эти формулы, чтобы ответить на вопрос, имеет ли смысл учет момента тормозящей силы в проделанных опытах.
Индивидуальные задания для членов бригады,
выполняющих лабораторную работу на одной установке
| Номер члена бригады | Индивидуальное задание |
Постройте, пользуясь формулой (4.6), график зависимости
момента тормозящей силы 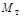 от величины h2. При расчете считайте величины h0 и h1, входящие в формулу, равными
h0 = 50 см, от величины h2. При расчете считайте величины h0 и h1, входящие в формулу, равными
h0 = 50 см, 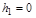 см. Численные значения радиуса шкива возьмите в таблице исходных данных, помещенной в Приложении и около лабораторной установки, на которой Вам предстоит выполнять опыты. Массу m считайте равной
массе подставки см. Численные значения радиуса шкива возьмите в таблице исходных данных, помещенной в Приложении и около лабораторной установки, на которой Вам предстоит выполнять опыты. Массу m считайте равной
массе подставки  (без подгрузков) (без подгрузков)
| |
Выполните задание, аналогичное заданию для первого но-
мера, но для массы m, равной сумме масс подставки и одно-
го подгрузка, 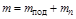
| |
Выполните задание, аналогичное заданию для первого но-
мера, но для массы m, равной сумме масс подставки и двух
подгрузков, 
|
Литература
1. Введение к настоящим методическим указаниям.
2. Савельев И.В. Курс общей физики. – М.: Наука, 1982. – Т. 1
(и последующие издания этого курса).
Лабораторная работа № 5
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛА
МЕТОДОМ КОЛЕБАНИЙ
Цель работы –определение момента инерции маятника с применением уравнения колебаний и исследование зависимости момента инерции от расстояния до условно выбранной точки А.
Описание установки
Установка представляет собой физический маятник, т. е. твердое тело, совершающее колебания под действием силы тяжести вокруг горизонтальной оси, не проходящей через его центр масс.
Физический маятник в данной работе состоит из барабана массой m1 с осью вращения О, стержня массой m2 и двух грузов с одинаковыми массами m3, которые можно закрепить в нужном положении на стержне (рис. 5.1).

а б
Рис. 5.1
Расчет момента инерции маятника
Пока сила тяжести Р, приложенная в центре масс С, направлена вдоль оси стержня (рис. 5.1, а), система находится в равновесии. Если отклонить стержень на некоторый малый угол 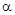 (рис. 5.1, б), то центр масс С поднимается на небольшую высоту и тело приобретает запас потенциальной энергии. На маятник относительно оси О, направление которой выбираем «к нам», будет при этом действовать момент силы тяжести, проекция которого на эту ось равна
(рис. 5.1, б), то центр масс С поднимается на небольшую высоту и тело приобретает запас потенциальной энергии. На маятник относительно оси О, направление которой выбираем «к нам», будет при этом действовать момент силы тяжести, проекция которого на эту ось равна
 , (5.1)
, (5.1)
где  ; L – расстояние между осью вращения О и центром масс С.
; L – расстояние между осью вращения О и центром масс С.
Вращающий момент М, создаваемый силой Р, при малых углах 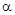 равен
равен
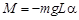 .
.
Он вызывает ускорение при вращательном движении маятника. Связь между этим ускорением и моментом сил дается основным уравнением динамики вращательного движения
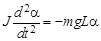 , (5.2)
, (5.2)
где J – момент инерции маятника относительно оси О.
Обозначим
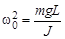 . (5.3)
. (5.3)
Тогда из уравнения (5.2) получим
 . (5.4)
. (5.4)
Уравнение (5.4) описывает колебательный процесс с циклической частотой 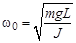 .
.
Период колебаний, следовательно, равен
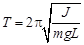 . (5.5)
. (5.5)
Из формулы (5.5) выразим момент инерции
 . (5.6)
. (5.6)
Если положение центра масс системы не изменяется, то величина L постоянна и в формулу (5.6) можно ввести постоянный коэффициент
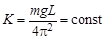 . (5.7)
. (5.7)
Измеряя время t, в течение которого происходит n полных колебаний, найдем период  . Подставляя T и K в (5.6), получаем рабочую формулу
. Подставляя T и K в (5.6), получаем рабочую формулу
 . (5.8)
. (5.8)
С помощью формулы (5.8) производятся косвенные измерения момента инерции физического маятника относительно оси О.
С другой стороны, момент инерции J зависит от положения грузов  на стержне. Переместим грузы
на стержне. Переместим грузы  по стержню так, чтобы они располагались симметрично относительно некоторой точки А. Эта математическая точка выбрана произвольно вблизи середины стержня. Центр масс системы при этом сохраняет свое местоположение. Будем считать размеры грузов
по стержню так, чтобы они располагались симметрично относительно некоторой точки А. Эта математическая точка выбрана произвольно вблизи середины стержня. Центр масс системы при этом сохраняет свое местоположение. Будем считать размеры грузов  малыми по сравнению с
малыми по сравнению с  и
и  (см. рис. 5.1). Тогда их можно рассматривать как материальные точки. В этом случае момент инерции системы определяется выражением
(см. рис. 5.1). Тогда их можно рассматривать как материальные точки. В этом случае момент инерции системы определяется выражением
 , (5.9)
, (5.9)
где  – момент инерции системы без грузов; x – расстояние груза
– момент инерции системы без грузов; x – расстояние груза  до точки А; l – расстояние точки А до оси вращения маятника О.
до точки А; l – расстояние точки А до оси вращения маятника О.
Преобразуя формулу (5.9), получаем
 , (5.10)
, (5.10)
где  – момент инерции маятника при положении грузов
– момент инерции маятника при положении грузов  в точке А.
в точке А.
Зависимость (5.10) будем проверять, получая величины J и JA экспериментально с помощью формулы (5.8).
Задание к работе
1. При подготовке к лабораторной работе получите расчетную формулу для погрешности косвенных измерений DJ момента инерции (см. Введение). Учтите, что момент инерции определяется с помощью рабочей формулы (5.8). Для упрощения вычислений можно считать, что коэффициент K в этой формуле измерен точно: DK = 0.
2. Подготовьте эскиз табл. 1 для статистической обработки прямых пятикратных измерений времени t (образец см. Введение табл. В.1).
3. Подготовьте эскиз табл. 2 для исследования зависимости J от x2.
4. Включите электронный секундомер. Нажатием кнопки «Режим» установите режим №3 (светится индикатор «Реж.3»), при этом отключится тормозное устройство, удерживающее тело.
5. Приступая к работе, поместите оба груза  в точке А (ее положение указано в таблице исходных данных, помещенной в Приложении и около лабораторной установки, на которой Вам предстоит работать).
в точке А (ее положение указано в таблице исходных данных, помещенной в Приложении и около лабораторной установки, на которой Вам предстоит работать).
6. Отклоните маятник рукой на небольшой угол  , и в момент отпускания маятника включите секундомер нажатием кнопки «Пуск». Отсчитав 10 полных колебаний маятника, остановите секундомер нажатием кнопки «Стоп». Запишите полученное время в таблицу измерений.
, и в момент отпускания маятника включите секундомер нажатием кнопки «Пуск». Отсчитав 10 полных колебаний маятника, остановите секундомер нажатием кнопки «Стоп». Запишите полученное время в таблицу измерений.
7. Проведите пятикратные измерения времени t десяти полных колебаний физического маятника, не меняя положение грузов.
8. Рассчитайте среднее время 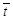 и определите доверительную погрешность измерения Dt.
и определите доверительную погрешность измерения Dt.
9. Используя рабочую формулу (5.8), определите значение момента инерции JA, а по формуле, полученной в п. 1 этого задания, определите погрешность измерения этой величины DJ. Результат запишите в виде 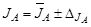 и занесите в табл. 2 для значения
и занесите в табл. 2 для значения  .
.
10. Раздвиньте грузы  симметрично относительно точки А на расстояние
симметрично относительно точки А на расстояние  (см. рис. 5.1). Рекомендуется расстояние
(см. рис. 5.1). Рекомендуется расстояние  взять равным тому значению, которое использовалось в индивидуальном задании. Проведите однократные измерения времени t десяти полных колебаний физического маятника.
взять равным тому значению, которое использовалось в индивидуальном задании. Проведите однократные измерения времени t десяти полных колебаний физического маятника.
11. Повторите опыт п. 7 при пяти различных расстояниях x.
12. Определите момент инерции маятника с помощью формулы (5.8) при различных расстояниях x. Результаты занесите в табл. 2.
13. Постройте график зависимости момента инерции маятника
от x2, пользуясь табл. 2. Нанесите на этот же график ожидаемую за-
висимость (5.10). Проведите сравнение и анализ полученных резуль-
татов.
Контрольные вопросы
1. В чем состоит цель данной работы?
2. Что такое момент инерции тела? В чем его физический смысл?
3. Сформулируйте и примените к данной работе основной закон динамики вращательного движения.
4. Что такое центр масс системы?
5. Почему местоположение центра масс маятника не меняется при изменении положения грузов  ?
?
6. Найдите момент инерции системы относительно центра масс, задав или измерив нужные для этого величины.
7. Сформулируйте закон сохранения энергии и запишите его применительно к физическому маятнику.
8. Как получить рабочую формулу (5.8) и зависимость (5.10)?
9. Как получить формулу для расчета погрешности косвенных измерений момента инерции?
10. Как формулируется теорема Штейнера? Как можно применить ее к исследуемой системе?
11. Почему предлагается построить график зависимости момента инерции от квадрата величины x?
12. Что такое момент силы  , угловая скорость
, угловая скорость  , угловое ускорение
, угловое ускорение 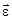 , угловое перемещение
, угловое перемещение 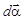 , как направлены эти векторы?
, как направлены эти векторы?
Индивидуальные задания для членов бригады,
выполняющих лабораторную работу на одной установке
| Номер члена бригады | Индивидуальное задание |
| Рассчитайте момент инерции маятника, состоящего из барабана и спицы с грузами, закрепленными на спице вплотную в точке А. Численные значения масс, размеров барабана и спицы возьмите в таблице исходных данных, помещенной в Приложении или около лабораторной установки, на которой Вам предстоит выполнять опыты | |
Рассчитайте момент инерции маятника, состоящего из барабана и спицы с грузами, закрепленными на спице на расстоянии  от точки А. Численные значения масс, размеров барабана и спицы возьмите в таблице исходных данных, помещенной в Приложении или около лабораторной установки, на которой Вам предстоит выполнять опыты от точки А. Численные значения масс, размеров барабана и спицы возьмите в таблице исходных данных, помещенной в Приложении или около лабораторной установки, на которой Вам предстоит выполнять опыты
| |
Выполните задание, аналогичное заданию для второго номера, но с другим значением расстояния 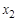 от точки А от точки А
|
Литература
Савельев И.В. Курс общей физики. – М.: Наука, 1982. – Т. 1 (и последующие издания этого курса).
Лабораторная работа № 6
ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ АДИАБАТЫ
МЕТОДОМ КЛЕМАНА И ДЕЗОРМА
Цель работы –изучение равновесных термодинамических процессов и теплоемкости идеальных газов, измерение показателя адиабаты классическим методом Клемана и Дезорма.
Равновесные и квазиравновесные тепловые процессы
Система молекул с постоянным количеством вещества n в объе-
ме V находится в «состоянии теплового равновесия», если во всех
микроскопически малых частях ее объема достаточно длительное время и давление Р, и температура Т одинаковы, т. е. являются параметрами состояния системы в целом. Состояние теплового равновесия может поддерживаться только в такой системе, через «границы» которой исключается перенос вещества и энергии. Такая система называется термодинамически изолированной [1].
В неизолированных системах тепловое равновесие отсутствует и наблюдается тот или иной тепловой процесс. Будучи изолированной, такая система за некоторое время спонтанно, благодаря тепловому движению молекул, придет в состояние равновесия [1]. Переход системы из неравновесного в равновесное состояние называют процессом релаксации и характеризуют временем релаксации. Так, неравномерность давления в изолированной системе на расстоянии 10 см исчезает весьма быстро – за 10–4–10–5 с, так как выравнивание давления происходит со скоростью звука (при 0 °С в воздухе скорость звука равна
330 м/с). Выравнивание температуры определяется теплопроводностью системы и протекает медленно. Время температурной релаксации идеальных газов имеет порядок t = 103 – 104 с на участке 10 см.
Все тепловые процессы являются, строго говоря, непрерывной последовательностью неравновесных состояний системы. Но если они протекают медленно по отношению ко времени релаксации (t >> t), то допустимо считать их непрерывной последовательностью равновесных состояний, так как, изменяясь постепенно, параметры состояния вследствие успевающей завершиться релаксации остаются практически одинаковыми во всех частях объема системы. Такие процессы называют равновесными. Они могут быть графически изображены на диаграмме состояний. Поскольку определяющим для системы является время температурной релаксации, то всякий равновесный процесс –принципиально очень медленный (t ® ¥). Такими, например, являют-
ся протекающие в условиях изменения температуры изобарический
(Р = const) и изохорический (V = const) процессы, если они осуществляются как равновесные.
Изотермический процесс протекает при постоянной температуре системы и принципиально является равновесным. На первый взгляд, при таком процессе нет необходимости учитывать время температурной релаксации. Однако и этот процесс должен проводиться очень медленно, чтобы осуществляемый теплообмен системы с внешней средой не приводил к изменению ее температуры. Как угодно малое приращение внутренней энергии dU системы, возникающее за счет подведения малого количества теплоты dQ ® dU, с учетом времени температурной релаксации полностью должно успеть перейти в работу системы dU®dA. Только в этом случае можно считать, что изотермический процесс выполняется: dQ ® dA, dU ® 0, dT ® 0 и T = const. Изотермический процесс – медленный принципиально. В идеале его определяют как бесконечно медленный. Реально тепловые процессы, включая изобарический и изохорический, проводят более или менее быстро, не обеспечивая полной температурой релаксации. В ряде случаев их можно рассматривать как равновесные только приближенно. Процессы, которые в определенных условиях с некоторым приближением можно рассматривать как равновесные, называют квазиравновесными. Такие процессы легче реализуются в системах с малым объемом, когда уменьшается время температурной релаксации, а также при сравнительно небольшом диапазоне изменения параметров состояния системы за время процесса.
Квазиравновесный адиабатный процесс
Адиабатный процесс проводится в системе с постоянным количест-вом вещества v при отсутствии теплообмена с внешней средой (dQ = 0). Для этого система должна быть термодинамически изолирована. При адиабатном процессе температура системы изменяется. Поэтому равновесный адиабатный процесс должен протекать настолько медленно, чтобы его длительность была много больше времени температурной релаксации системы, т. е. t >>  . Отсюда следует часто трудно выполнимое, жесткое требование к качеству тепловой изоляции системы.
. Отсюда следует часто трудно выполнимое, жесткое требование к качеству тепловой изоляции системы.
Чтобы избежать этого затруднения, на практике адиабатный процесс проводят как квазиравновесный: объем системы изменяют настолько быстро, чтобы за время длительности процесса можно было пренебречь теплообменом системы с внешней средой, т. е. dQ ® 0. Ясно, что температурная релаксация системы за такой интервал времени не завершается, и неравномерность температуры в разных частях объема не позволяет считать такой адиабатный процесс равновесным. Однако, выбирая объем системы достаточно малым и проводя процесс при незначительном изменении давления, объема и температуры системы, можно считать его квазиравновесным.
Адиабатный процесс в системе идеального газа с постоянным числом одинаковых молекул аналитически записывается либо уравнением (6.1), либо уравнением (6.2)
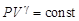 , (6.1)
, (6.1)
 , (6.2)
, (6.2)
где показатель адиабаты g определяется только «числом степеней свободы» i [1] молекулы газа и равен отношению теплоемкостей газа при постоянном давлении СP (изобарический процесс) и при постоянном объеме СV (изохорический процесс)
 , (6.3)
, (6.3)
 . (6.4)
. (6.4)
Рассмотрим относительное изменение параметров состояния системы, удовлетворяющее условию проведения квазиравновесного адиабатного процесса.
Задавшись приращениями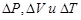 давления, объема и температуры, из формул (6.1) и (6.2) получим соответственно уравнения
давления, объема и температуры, из формул (6.1) и (6.2) получим соответственно уравнения


из которых следует, что относительные изменения объема и темпе-
ратуры зависят от относительного изменения давления следующим образом:
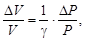

Для одно-, двух- и трехатомных молекул число степеней свободы соответственно равно i = 3, i = 5, i = 6. Пусть i = 5 и g = 1,4.
Условие квазиравновесия требует, чтобы приращения параметров состояния системы были малы. Особенно это относится к температуре. Пусть 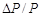 = 0,01, тогда
= 0,01, тогда  V /V= 0,007 и
V /V= 0,007 и  Т/Т = 0,003. Проведем количественную оценку приращения параметров.
Т/Т = 0,003. Проведем количественную оценку приращения параметров.
В качестве наименьшего давления в системе примем атмосферное дав-ление Р = 1,01×105 Па. Тогда приращение давления 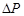 = 1,01×103 Па =
= 1,01×103 Па =
= 103 мм вод. ст. Оно может быть измерено непосредственно U-об-разным жидкостным манометром, один вход которого соединен c системой, а второй, открытый – непосредственно с внешней средой.
Если в исходном состоянии система имеет комнатную температуру, например Т = 300 К, то по окончании адиабатного процесса расширения температура уменьшится на  Т = 1К (или на 1 °С). Столь незначительное уменьшение температуры позволяет считать ее приблизительно постоянной. Следовательно, адиабатный быстропротекающий процесс в этих условиях вполне можно рассматривать как квазиравновесный.
Т = 1К (или на 1 °С). Столь незначительное уменьшение температуры позволяет считать ее приблизительно постоянной. Следовательно, адиабатный быстропротекающий процесс в этих условиях вполне можно рассматривать как квазиравновесный.
Метод измерения показателя адиабаты
Технически более просто осуществляется адиабатный процесс расширения газа из равновесного состояния 1, при котором температура системы Т1 равна температуре То окружающей внешней среды,
а давление Р1 = Ро +  Р1 превышает значение атмосферного давле-
Р1 превышает значение атмосферного давле-
ния Ро. По окончании адиабатного процесса в квазиравновесном состоянии 2 температура будет Т2 = То –  Т, а давление в системе Р2 = Ро.
Т, а давление в системе Р2 = Ро.
Для эксперимента необходима система, способная спонтанно увеличить свой объем при неизменном количестве вещества в нем. Такая система не может быть ограничена стенками какого-либо сосуда, имеющего постоянный объем. В то же время избыточное давление в системе можно обеспечить только тогда, когда она заключена в таком сосуде. Для устранения этого противоречия выберем систему молекул внутри сосуда, но занимающую при избыточном давлении Р1 только небольшую часть V1 объема сосуда, как показано на рис. 6.1, где выделенная система условно ограничена круговой линией.

Рис. 6.1
В исходное равновесное состояние 1 система приходит после предварительного сжатия (подкачка газа может быть осуществлена насосом) и последующей релаксации (в течение нескольких минут), когда в условиях теплового равновесия с внешней средой весь газ в сосуде будет иметь температуру Т1 = То и установившееся давление Р1.
В процессе быстрого адиабатного расширения системы, производимого резким соединением через открывающийся клапан К полости сосуда с внешней средой, теплообменом газа в сосуде и, тем более, в выделенной системе, можно пренебречь (dQ ® 0). Внутренняя энергия системы уменьшается на величину расходуемую на работу А расширения системы: DU® А. На диаграмме (рис. 6.2) адиабатный процесс перехода из состояния 1 в состояние 2 показан графически.
расходуемую на работу А расширения системы: DU® А. На диаграмме (рис. 6.2) адиабатный процесс перехода из состояния 1 в состояние 2 показан графически.
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
| |
|
|
|
|

Рис. 6.2
Из уравнения (6.1) адиабатного процесса для состояний 1 и 2 следует равенство 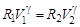 , но так как Р2 = Ро, то можно записать, что
, но так как Р2 = Ро, то можно записать, что 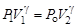 . Отсюда найдем, что показатель адиабаты
. Отсюда найдем, что показатель адиабаты
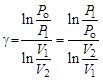 . (6.5)
. (6.5)
В формуле (6.5)
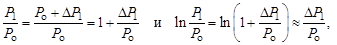
так как
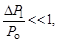
а отношение объемов V2 /V1 остается неизменным.
Особенностъ метода Клемана и Дезорма состоит в том, что после адиабатного процесса из состояния 2 система, сохраняя постоянный объем, изохорически в течение некоторого времени переходит в равновесное состояние 3 (см. рис. 6.1), при котором в условиях теплового равновесия с внешней средой она приобретает температуруТо этой среды: V3 = V2, Т3 = То и Р3 > Р0. Таким образом, состояния 1 и 3 являются изотермическими (Т1 = То и Т3 = То), т. е. принадлежат некоторой теоретической изотерме (на рис. 6.2 – пунктирная линия РV = const). Поэтому для этих состояний можно записать равенство Р1V1 = Р3V3, либо, учитывая, что V3 = V2, равенство Р1V1 = Р3V2. Отсюда следует, что в формуле (6.3) неизвестное отношение объемов можно заменить отношением давлений

где  – приращение давления при изохорическом процессе. Учитывая, что
– приращение давления при изохорическом процессе. Учитывая, что 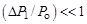 и
и  получаем
получаем
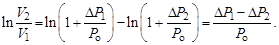
Подставив найденные выражения для логарифмов в формулу (6.5) запишем в окончательном виде уравнение, позволяющее производить измерение показателя адиабаты по методу Клемана и Дезорма,
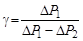 .
.
Измерения с помощью формулы (6.6) – косвенные. Однако при обработке результатов измерений их следует рассматривать как прямые, в каждом эксперименте вычисляя значение g1, g2 ,…gi,…gn, а затем находя среднее значение 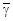 и погрешность Dg. Эта особенность объясняется невоспроизводимостью от опыта к опыту исходного состояния 1 (Р1, V1, Т1) системы, которое образуется спонтанно из неравновесного состояния 0, в значительной мере зависящего от способа и режима нагнетания воздуха в сосуд.
и погрешность Dg. Эта особенность объясняется невоспроизводимостью от опыта к опыту исходного состояния 1 (Р1, V1, Т1) системы, которое образуется спонтанно из неравновесного состояния 0, в значительной мере зависящего от способа и режима нагнетания воздуха в сосуд.
Экспериментальная установка

Рис. 6.3
Установка, изображенная на рис. 6.3, содержит стеклянный со-
суд 1 с пробкой 2, в которой установлены подпружинный клапан 3,
а также соединительные трубки жидкостного U-образного манометра 4 и ручного насоса 5, который сообщается с сосудом через вентиль 6. Схема установки показананарис. 6.3. Необходимо соблюдать следующий порядок работы:
1) открыть вентиль 6;
2) насосом 5 малыми порциями накачать воздух в сосуд 1, создав давление, при котором в открытом колене манометра 4 уровень жидкости устанавливается вблизи верхнего деления шкалы. Следить, чтобы жидкость из трубки манометра не вылилась наружу;
3) закрыть вентиль 6;
4) в течение 2–3 мин дать системе придти в состояние равновесия (исходное состояние 1) при температуре внешней среды; измерить приращение давления DР1 по шкале манометра 4;
5) резким нажатием клапана 3 осуществить быстрое адиабатическое расширение системы; в момент выравнивания уровней жидкости в обоих коленах манометра клапан 3 отпустить;
6) в течение 2–3 мин осуществить изохорический процесс, по окончании которого система приходит в состояние 3 равновесия при температуре внешней среды, а давление Р3 стабилизируется. Измерить приращение давления DР2 по шкале манометра 4;
7) с помощью формулы (6.6) вычислить значение показателя адиабаты.
Задание к работе
1. Тщательно изучить равновесные и квазиравновесные тепловые процессы, включая адиабатный процесс, а также понятие о степенях свободы молекул, вопросы теплоемкости идеальных газов, первое начало термодинамики.
2. Изучить метод Клемана и Дезорма, применяемый для измерения показателя адиабаты.
3. Провести 10–15-кратное измерение показателя адиабаты с помощью формулы (6.6), определяя приращения давления DР1 и DР2 и вычисляя g.
4. Вычислить среднее значение показателя адиабатыи, при доверительной вероятности Р = 90 %, случайную погрешность измерений, считая их прямыми (см. Введение).
5. Найти теоретическое значение показателя адиабаты для двухатомного газа и сравнить его с экспериментально полученным значением.
Контрольные вопросы
1. Дайте определение термодинамически изолированной системы.
2. Какие состояния системы называют равновесными?
3. Что такое процесс релаксации системы, время релаксации системы?
4. Какие процессы называют равновесными и квазиравновесными?
5. Дайте определение всех изопроцессов и адиабатного процесса, напишите уравнения этих процессов, приведите их графическое изображение на диаграмме состояний.
6. Охарактеризуйте изопроцессы и адиабатный процесс с точки зренияих равновесности.
7. Что называют степенями свободы молекул и чему равно их число для одно-, двух- и трехатомных молекул?
8. Дайте определения теплоемкости, удельной и молярной теплоемкостей системы. Чему равны молярные теплоемкости идеального газа при изобарическом и изохорическом процессах? Как эти теплоемкости связаны друг с другом?
9. Изложите сущность метода Клемана и Дезорма для измерения показателя адиабаты.
10. Что называется показателем адиабаты, чем он определяетсяи как связан с теплоемкостями идеального газа при изобарическом и изохорическом процессах?
Литература
Савельев И.В. Курс общей физики. – М.: Наука, 1982. – T. 12
(и последующие издания этого курса).
Приложение
Исходные данные для лаборатории,
расположенной в IV корпусе НГТУ,
Ауд. № 205
Лабораторная работа № 1 Определение скорости пулиЛабораторная работа № 3
Определение момента инерции маятника Обербека
Масса грузов для спиц вместе с винтом (4 шт.) mгр.сп = (58 ± 1) г Масса груза подставки mпод = (42.2 ± 0.2) г Масса каждого подгрузка (2 шт.) mп = (15.8 ± 0.3) гДиаметр малого шкива d = (25.0 ± 0.1) мм
Ускорение свободного падения g = (9.80 ± 0.05) м/с2
Исходные данные для лаборатории,
расположенной в IV корпусе НГТУ,
Ауд. № 234
Лабораторная работа № 5
Определение момента инерции методом колебаний
Расстояние от оси вращения до центра масс физического маятника L = (45 ± 2) мм Рекомендуемое расстояние от оси вращенияМетодические указания
Редактор Н. В. Городник– Конец работы –
Используемые теги: Механика, термодинамика0.069
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: МЕХАНИКА И ТЕРМОДИНАМИКА
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов