рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Механика
- /
- МЕХАНИКА
Реферат Курсовая Конспект
МЕХАНИКА
МЕХАНИКА - раздел Механика, Министерство Образования И Науки Российской Федерации Федеральное Аг...
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
«Оренбургский государственный университет»
Кафедра радиофизики и электроники
Э.К.Гадаева
МЕХАНИКА
Методические указания к лабораторным работамГадаева, Э.К.
Гадаева; Оренбургский гос. ун-т. – Оренбург: ОГУ, 2010.- 153 с. Методические указания содержат основные понятия и методы, используемых при обработке результатов экспериментальных…Содержание
1 Лабораторная работа №1. Законы Ньютона...…………………………………..5
1.1 Теоретическая часть……………………………………………………………5
1.2 Экспериментальная часть………………………………………………………9
1.3 Контрольные вопросы……………………………………………………..…..16
1.4 Рекомендуемая литература……………………………………………………16
2 Лабораторная работа №2. Законы сохранения импульса и механической энергии…………………………………………………………...……………...………17
2.1 Теоретическая часть…………………………………………………..……….17
2.2 Экспериментальная часть…………………………………………………..…21
2.3 Контрольные вопросы…………………………………………….………..….26
2.4 Рекомендуемая литература……………………………………………………26
3 Лабораторная работа №3. Маятники……………….………………….……….27
3.1 Теоретическая часть………………………………………………………...…27
3.2 Экспериментальная часть……………………………………………………..31
3.3 Контрольные вопросы………………………………………….………….…..36
3.4 Рекомендуемая литература……………………………………………………37
4 Лабораторная работа №4. Основное уравнение динамики вращательного движения………..………………..………………………………………..……..……..38
4.1 Теоретическая часть…………………….…………………………...…………38
4.2 Экспериментальная часть…………………………………………………...…42
4.3 Контрольные вопросы……………………………………………….……..….50
4.4 Рекомендуемая литература……………………………………………...…….50
5 Лабораторная работа №5. Теорема Гюйгенса-Штейнера……………….……..51
5.1 Теоретическая часть……………………………………….………….……..…51
5.2 Экспериментальная часть…………………………………………………...…59
5.3 Контрольные вопросы……………………………………………………….…62
5.4 Рекомендуемая литература…………………………………………………….62
6 Лабораторная работа №6. Определение момента инерции колеса…………....63
6.1 Теоретическая часть………………………………………………………...….63
6.2 Экспериментальная часть……………………………………………………...71
6.3 Контрольные вопросы………………………………………………………….73
6.4 Рекомендуемая литература…………………………………………………….73
7 Лабораторная работа №7. Закон сохранения момента количества движения……………………………………………………………………………….......74
7.1 Теоретическая часть……………………………………………………………74
7.2 Экспериментальная часть………………………………………………….…..78
7.3 Контрольные вопросы……………………………………………………….…87
7.4 Рекомендуемая литература…………………………………………………….88
8 Лабораторная работа №8. Изучение деформации растяжения и сжатия……..89
8.1 Теоретическая часть……………………………………………………………89
8.2 Экспериментальная часть………………………………………………….…..99
8.3 Контрольные вопросы………………………………………………………...105
8.4 Рекомендуемая литература…………………………………………………...105
9 Лабораторная работа №9. Изучение деформации кручения и сдвига…….…106
9.1 Теоретическая часть…………………………………………………………..106
9.2 Экспериментальная часть…………………………………………………….111
9.3 Контрольные вопросы…………………………………………………..….…116
9.4 Рекомендуемая литература…………………………………………………...116
10 Лабораторная работа №10. Коэффициент качения…………………….……117
10.1 Теоретическая часть……………………….…………………………….…..117
10.2 Экспериментальная часть……………………………………………….…..122
10.3 Контрольные вопросы……………………………………….………………125
10.4 Рекомендуемая литература………………………………………………….125
11 Лабораторная работа №11. Тензор инерции твердого тела…...……………126
11.1 Теоретическая часть………………………………………………………....126
11.2 Экспериментальная часть………………………………………………..….133
11.3 Контрольные вопросы…………………………………………………….…138
11.4 Рекомендуемая литература………………………………………………….138
12 Лабораторная работа №12. Свободные и вынужденные колебания…….…139
12.1 Теоретическая часть……………………………………………….………...139
12.2 Экспериментальная часть………………………………………….………..144
12.3 Контрольные вопросы……………………………………………….………152
12.4 Рекомендуемая литература………………………………………………….152
Приложение А…………………………………………………………….…..…...153
Лабораторная работа №1. Законы Ньютона
Цель работы: 1) изучение законов равноускоренного движения.
2) изучение законов динамики поступательного движения.
3) проверка второго закона Ньютона с помощью машины Атвуда.
Теоретическая часть
В кинематике, где речь идет лишь об описании движений и не затрагивается вопрос о причинах, вызывающих эти движения, никакой принципиальной разницы между различными системами отсчета нет, и все они в этом отношении равноправны. Иначе обстоит дело в динамике: законы механики в разных системах отсчета имеют, вообще говоря, различный вид и может оказаться, что в произвольной системе отсчета законы даже совсем простых явлений будут весьма сложными.
Можно предположить, что существует такая система отсчета, в которой ускорение материальной точки целиком обусловлено только взаимодействием ее с другими телами. Свободная материальной точка, не подверженная действию никаких других тел, движется относительно такой системы отсчета прямолинейно и равномерно, или, как говорят, по инерции. Такую систему отсчета называют инерциальной.
Существование инерциальных систем отсчета подтверждается опытом. Первоначальными опытами было установлено, что такой системой отсчета является Земля. Последующие более точные опыты (например, опыт Фуко) показали, что эта система отсчета не совсем инерциальная[1], а именно: были обнаружены ускорения, существование которых нельзя объяснить действием каких-либо определенных тел. В то же время наблюдения над ускорениями планет показали инерциальность гелиоцентрической системы отсчета, связанной с центром Солнца и «неподвижными» звездами.
Любая другая система отсчета, движущаяся равномерно и прямолинейно относительно гелиоцентрической системы, является также инерциальной. Системы отсчета, движущиеся с ускорением относительно инерциальных систем, называют неинерциальными.
Для инерциальных систем отсчета справедлив принцип относительности, согласно которому все инерциальные системы по своим механическим свойствам эквивалентны друг другу. Во всех инерциальных системах отсчета свойства пространства и времени одинаковы. Данное утверждение составляет содержание принципа относительности Галилея – одного из важнейших принципов ньютоновской механики.
В качестве первого закона движения Ньютон принял закон инерции:
Тело (материальная точка), не подверженное внешним воздействиям, либо находится в покое, либо движется прямолинейно и равномерно, т.е. по инерции.
Одной из важнейших характеристик силы является ее материальное происхождение. Все силы, встречающиеся в природе, известные в настоящее время,… Электромагнитные и гравитационные силы, напротив, являются силами… Опыт показывает, что всякое тело «оказывает сопротивление» при любых попытках изменить его скорость – как по модулю,…Произведение массы материальной точки на ее ускорение равно действующей на нее силе.
Уравнение (1.1) называют уравнением движения материальной точки. На всякую материальную точку зачастую действует несколько сил, поэтому в уравнении… Уравнение движения можно представить и в следующем виде:Экспериментальная часть
Описание экспериментальной установки
Экспериментальная установка, получившая название «машина Атвуда», представляет собой вращающийся с максимально малым трением легкий блок, через который перекинута тонкая нить с грузами массой  и
и  (рисунок 1.2). На каждый груз действуют две силы — сила тяжести и сила натяжения нити, под действием этих сил грузы и начинают свое движение. Меняя массы грузов, можно получать различные ускорения.
(рисунок 1.2). На каждый груз действуют две силы — сила тяжести и сила натяжения нити, под действием этих сил грузы и начинают свое движение. Меняя массы грузов, можно получать различные ускорения.

Рисунок 1.2 - Схема машины Атвуда
При дальнейшем анализе мы предполагаем, что нить невесома и нерастяжима, сопротивление в оси блока отсутствует, масса блока равна нулю, сопротивление воздуха отсутствует.
Выберем систему координат так, как показано на рисунке 1.2. Уравнения движения каждого груза в этой системе координат имеют вид
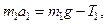 (1.5)
(1.5)
- (1.6)
(1.6)
В связи с тем, что нить нерастяжима (x1+x2 = l = const), ускорения обоих грузов равны по величине и противоположны по направлению, поэтому уравнение кинематической связи можно записать в виде
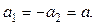 (1.7)
(1.7)
Из предположений, сделанных ранее, следует также, что натяжения нитей одинаковы, то есть
 (1.8)
(1.8)
Пусть  , тогда, решая полученную систему уравнений, получаем значение ускорения:
, тогда, решая полученную систему уравнений, получаем значение ускорения:
 (1.9)
(1.9)
и величину силы натяжения нити:
 (1.10)
(1.10)
Ускорение тел системы всегда меньше ускорения свободного падения и меняется при изменении соотношения между массами обоих грузов.
Для выбранной системы тел можно учесть влияние массы блока и силы трения в его оси. Система уравнений в этом случае дополняется уравнением вращательного движения блока и уравнением кинематической связи между угловым ускорением блока и ускорением одного из грузов. Очевидно, что силы натяжения нитей слева и справа от блока будут отличаться. Окончательно система уравнений имеет вид:
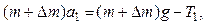 (1.11)
(1.11)
 (1.12)
(1.12)
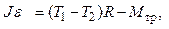 (1.13)
(1.13)
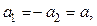 (1.14)
(1.14)
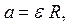 (1.15)
(1.15)
где  — момент инерции блока,
— момент инерции блока,
m0 и R — его масса и радиус,
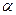 — коэффициент, зависящий от распределения массы (от формы блока),
— коэффициент, зависящий от распределения массы (от формы блока),
 — угловое ускорение блока,
— угловое ускорение блока,
Mтр — момент сил трения в оси.
Решая систему уравнений (1.11)–(1.15), получаем значение ускорения
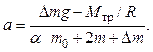 (1.16)
(1.16)
Очевидно, что ненулевые значения силы трения в оси и массы блока уменьшают величину ускорения по сравнению с идеальным случаем.
Машина Атвуда, используемая в данной лабораторной работе, состоит из прикрепленной к основанию вертикальной стойки, на которую нанесена шкала (рисунок 1.3). На верхнем конце стойки имеется легкий блок, способный вращаться с малым трением. Через блок перекинута легкая нить, к концам которой прикреплены два одинаковых груза 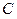 и
и  . На груз
. На груз 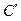 можно помещать добавочные грузы в виде тонких пластин (перегрузки), в результате этого система грузов начинает двигаться с некоторым ускорением. Меняя массу перегрузка, можно менять ускорение системы. После того, как груз
можно помещать добавочные грузы в виде тонких пластин (перегрузки), в результате этого система грузов начинает двигаться с некоторым ускорением. Меняя массу перегрузка, можно менять ускорение системы. После того, как груз  с перегрузком проходит некоторое расстояние
с перегрузком проходит некоторое расстояние  , перегрузок снимается с помощью кронштейна
, перегрузок снимается с помощью кронштейна  . После этого грузы начинают двигаться равномерно. На стойке укреплены два фотоэлектрических датчика, соединенные с таймером. При этом верхний фотодатчик соединен с кронштейном G. Фотодатчики могут крепиться на стойке в разных положениях. Система грузов удерживается в состоянии покоя специальной фрикционной муфтой, управляемой с помощью электромагнита.
. После этого грузы начинают двигаться равномерно. На стойке укреплены два фотоэлектрических датчика, соединенные с таймером. При этом верхний фотодатчик соединен с кронштейном G. Фотодатчики могут крепиться на стойке в разных положениях. Система грузов удерживается в состоянии покоя специальной фрикционной муфтой, управляемой с помощью электромагнита.
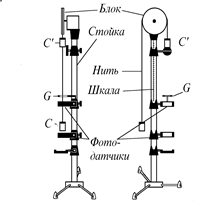
Рисунок 1.3 - Схема экспериментальной установки
Для измерения времени равномерного движения установка снабжена таймером. При нажатии на клавишу "сброс" происходит обнуление табло таймера. В исходном состоянии систему следует затормозить, включив электромагнит фрикционной муфты с помощью выносного выключателя. При выключении электромагнита происходит освобождение системы, грузы приходят в движение. После этого нужно нажать кнопку "пуск" таймера для подготовки его к измерению. Во время прохождения телом  верхнего фотодатчика таймер запускается, он начинает отсчитывать время. Импульс от нижнего фотоэлектрического датчика останавливает работу таймера, результат высвечивается на табло.
верхнего фотодатчика таймер запускается, он начинает отсчитывать время. Импульс от нижнего фотоэлектрического датчика останавливает работу таймера, результат высвечивается на табло.
Перед выполнением эксперимента следует убедиться, что груз  может свободно опускаться, не касаясь кронштейна G и фотодатчиков. В противном случае при помощи винтов, крепящих кронштейн и фотодатчики, следует провести необходимые регулировки.
может свободно опускаться, не касаясь кронштейна G и фотодатчиков. В противном случае при помощи винтов, крепящих кронштейн и фотодатчики, следует провести необходимые регулировки.
Проведение эксперимента
Упражнение 1. Анализ закона движения и определение ускорения
Исходя из анализа движения системы тел, можно предположить, что реальное движение тел на участке L1 будет равнопеременным. В этом случае закон движения, т.е. зависимость координаты тела от времени, будет иметь вид

где  — координата, от которой груз
— координата, от которой груз 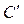 начинает свое движение. Учитывая, что при равнопеременном движении скорость меняется по закону
начинает свое движение. Учитывая, что при равнопеременном движении скорость меняется по закону
 ,
,
получаем
 (1.17)
(1.17)
где  — скорость груза
— скорость груза  в момент снятия перегрузка и включения таймера,
в момент снятия перегрузка и включения таймера,  — координата верхнего фотодатчика. Если в системе отсутствуют силы трения, то с этой же скоростью тело
— координата верхнего фотодатчика. Если в системе отсутствуют силы трения, то с этой же скоростью тело 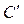 будет проходить расстояние между фотодатчиками после снятия с него перегрузка, т. е.
будет проходить расстояние между фотодатчиками после снятия с него перегрузка, т. е.
 , (1.18)
, (1.18)
где 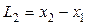 — расстояние между двумя фотодатчиками (x2 — координата нижнего фотодатчика),
— расстояние между двумя фотодатчиками (x2 — координата нижнего фотодатчика),
t2 — время движения на этом участке пути.
Измерения
2 Во время прохождения телом верхнего фотодатчика таймер запускается, он начинает отсчитывать время. Импульс от нижнего фотоэлектрического датчика… Систему тел приводят в движение, для чего выключают электромагнит фрикционной… Таблица 1.1 № опыта L1, 10-2 м t2, с v1, м/с v12, (м/с)2 …Измерения
2 Поместите на груз один из перегрузков, имеющихся в вашем распоряжении. 3 Определите 3–5 раз время t2 прохождения промежутка . Результаты измерений… Проведите аналогичные измерения, положив на груз два, а затем три перегрузка. Результаты измерений также внесите в…Обработка результатов
где — число измерений. 2 Вычислить выборочное стандартное отклонение среднего арифметического значенияОсновные итоги работы
На основании выполнения работы должно быть показано, что движение системы тел под действием постоянной силы является равноускоренным, показано выполнение 2-го закона Ньютона. Должны быть проанализированы систематические погрешности при проведении эксперимента (по указанию преподавателя).
Контрольные вопросы
1 Что такое инерциальные и неинерциальные системы отсчета? Сформулируйте I-й закон Ньютона.
2 Что такое масса, каковы способы ее измерения?
3 Что такое сила, как ее измерить?
4 Сформулируйте II-й закон Ньютона.
5 Сформулируйте III-й закон Ньютона.
6 Охарактеризуйте гравитационное фундаментальное взаимодействие.
7 Охарактеризуйте электромагнитное фундаментальное взаимодействие.
8 Дайте определение, формулу, покажите точку приложения силы тяжести, упругой силы, силы трения.
9 Выведите формулу для веса тела 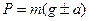 .
.
10 Покажите применение алгоритма решения задач по динамике для случая, предложенного преподавателем (например, движение связанных тел, перекинутых через блок, и движущихся по наклонным плоскостям с разными углами наклона к горизонту).
11 Границы применимости классической механики.
12 Сформулируйте условия, при которых получены основные соотношения задачи. Как эти условия влияют на вид решаемой системы уравнений?
Рекомендуемая литература
1.4.1 Иродов, И.Е. Механика. Основные законы механики / И.Е.Иродов. - М.: Бином, 2009. – 310 с. - ISBN 978-5-9963-0063-1.
1.4.2 Савельев, И.В. Курс общей физики: в 5 кн. / И.В.Савельев. – М.: АСТРЕЛЬ: АСТ, 2005. – Кн. 1: Механика. – 336 с. - ISBN 5-271-01034-1.
1.4.3 Сивухин, Д.В. Общий курс физики: в 3 т. / Д.В.Сивухин. - М.: Физматлит, 2002. – Т. 1: Механика. – 560 с. - ISBN 5-89155-078-4.
1.4.4 Трофимова, Т.И. Физика в таблицах и формулах / Т.И. Трофимова. – М.: Академия, 2006. – 448 с. - ISBN 5-7695-2277-1.
Лабораторная работа №2. Законы сохранения импульса и механической энергии
Цель работы:1) изучение закона сохранения импульса и механической энергии.
2) использование законов сохранения движения для решения практических задач механики.
Теоретическая часть
Тела, образующие механическую систему, могут взаимодействовать как между собой, так и с телами, не принадлежащими данной системе. В соответствии с этим силы, действующие на тела системы, можно подразделить на внутренние и внешние. Внутренними мы будем называть силы, с которыми на данное тело воздействуют остальные тела системы, внешними – силы, обусловленные воздействием тел, не принадлежащих системе. В случае, если внешние силы отсутствуют, система называется замкнутой.
Для замкнутых систем существуют такие функции координат и скоростей образующих систему частиц, которые сохраняют при движении постоянные значения. Эти функции носят название интегралов движения.
Для системы из N частиц, между которыми нет жестких связей, можно образовать 6N-1 интегралов движения. Однако интерес представляют только те из них, которые обладают свойством аддитивности. Это свойство заключается в том, что значение интеграла движения для системы, состоящей из частей, взаимодействием которых можно пренебречь, равно сумме значений для каждой из частей в отдельности. Аддитивных интегралов движения имеется три. Один из них называется энергией, второй – импульсом, третий – моментом импульса.
Итак, для замкнутых систем имеют место три закона сохранения – закон сохранения энергии, закон сохранения импульса и закон сохранения момента импульса. Эти законы тесно связаны с основными свойствами пространства и времени.
Законы сохранения представляют собой мощное орудие исследования. Часто точное решение уравнений движения оказывается крайне сложным. В этих случаях с помощью законов сохранения можно и без решения уравнений движения получить ряд важных данных о протекании механических явлений. Законы не зависят от характера действующих сил. Поэтому с их помощью можно получить ряд важных сведений о поведении механических систем даже в тех случаях, когда силы оказываются неизвестными. Подчеркнем, что законы сохранения энергии, импульса и момента импульса являются точными законами, строго выполняющимися также и в релятивистской области.
Импульс частицы. Закон сохранения импульса. По определению импульс частицы
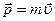 ,
,
где  и
и  - ее масса и скорость. Воспользовавшись понятием импульса, запишем основное уравнение динамики в иной форме:
- ее масса и скорость. Воспользовавшись понятием импульса, запишем основное уравнение динамики в иной форме:
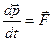 , (2.1)
, (2.1)
т.е. производная импульса материальной точки по времени равна действующей на нее силе. В частности, если  , то
, то  .
.
Уравнение (2.1) позволяет найти приращение импульса частицы за любой промежуток времени, если известна зависимость силы 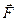 от времени. Проинтегрировав это выражение по времени, найдем приращение импульса частицы за конечный промежуток времени
от времени. Проинтегрировав это выражение по времени, найдем приращение импульса частицы за конечный промежуток времени  :
:
 . (2.2)
. (2.2)
Величину, стоящую в правой части этого уравнения, называют импульсом силы. Таким образом, приращение импульса частицы за любой промежуток времени зависит не только от значения силы, но и от продолжительности ее действия, или, другими словами, равно импульсу силы за это время. В частности, если 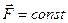 , то вектор
, то вектор 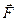 можно вынести из-под интеграла и тогда
можно вынести из-под интеграла и тогда  .
.
Рассмотрим произвольную систему частиц. В общем случае частицы этой системы могут взаимодействовать как между собой, так и с телами, не входящими в данную систему. Импульс системы есть векторная сумма импульсов ее отдельных частиц:
 , (2.3)
, (2.3)
где 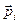 - импульс
- импульс  -й частицы.
-й частицы.
Продифференцируем выражение (2.3) по времени:
 .
.
Согласно (2.1),
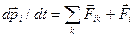 ,
,
где  - силы, действующие на
- силы, действующие на  -ю частицу со стороны других частиц системы (внутренние силы);
-ю частицу со стороны других частиц системы (внутренние силы);
 - сила, действующая на эту же частицу со стороны других тел, не входящих в рассматриваемую систему (внешние силы). Подставив последнее выражение в предыдущее, получим
- сила, действующая на эту же частицу со стороны других тел, не входящих в рассматриваемую систему (внешние силы). Подставив последнее выражение в предыдущее, получим
 .
.
Двойная сумма справа – это сумма всех внутренних сил. В соответствии с третьим законом Ньютона силы взаимодействия между частицами системы попарно одинаковы по модулю и противоположны по направлению. Поэтому результирующая сила в каждой паре взаимодействия равна нулю, а значит, равна нулю и векторная сумма всех внутренних сил. В результате последнее выражение принимает следующий вид:
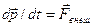 , (2.4)
, (2.4)
где 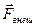 - результирующая всех внешних сил,
- результирующая всех внешних сил, 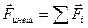 .
.
Согласно выражению (2.4), импульс системы может изменяться под действием только внешних сил. Внутренние силы не могут изменить импульс системы. Отсюда непосредственно вытекает закон сохранения импульса:
импульс замкнутой системы частиц остается постоянным, т.е. не меняется со временем:
 . (2.5)
. (2.5)
При этом импульсы отдельных частиц или частей замкнутой системы могут меняться со временем. Однако эти изменения всегда происходят так, что приращение импульса одной части системы равно убыли импульса оставшейся части системы.
Механическая энергия. Рассмотрим систему, состоящую из одной частицы, и напишем ее уравнение движения:
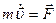 . (2.6)
. (2.6)
Умножив уравнение (2.6) на перемещение частицы  , получим
, получим
 (2.7)
(2.7)
Произведя такую замену в (2.6), придем к соотношению

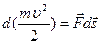 . (2.8)
. (2.8)
Если система замкнута, т.е. 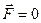 , то
, то  , а сама величина
, а сама величина
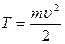 (2.9)
(2.9)
остается постоянной. Эта величина называется кинетической энергией частицы. В случае изолированной частицы кинетическая энергия является интегралом движения.
Величина, стоящая в правой части выражения (2.8) называется работой, совершаемой силой 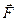 на пути
на пути 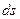 :
:
 . (2.10)
. (2.10)
Скалярное произведение (2.10) можно представить в виде произведения проекции силы на направление перемещения  и элементарного пути
и элементарного пути 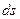 :
:
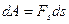 .
.
Проинтегрируем выражение (2.8) вдоль некоторой траектории от точки 1 до точки 2:
 .
.
Левая часть представляет собой разность значений кинетической энергии в точках 2 и 1, т.е. приращение кинетической энергии на пути 1-2:
 ,
,
а правая – работа силы 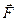 на пути 1-2.
на пути 1-2.
Итак, работа результирующей всех сил, действующих на частицу, идет на приращение кинетической энергии частицы:
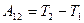 . (2.11)
. (2.11)
Если в каждой точке пространства на помещенную туда частицу действует сила, то частица находится в поле сил, например, частица может находиться в поле сил тяжести или в поле сил сопротивления. Поле, остающееся постоянным во времени, называют стационарным. Отметим, что поле стационарное в одной системе отсчета может быть нестационарно в другой системе отсчета. Работа, которую совершают силы поля при перемещении частицы из точки 1 в точку 2, зависит, вообще говоря, от пути между этими точками. Вместе с тем имеются стационарные силовые поля, в которых работа, совершаемая над частицей силами поля, не зависит от пути между точками 1 и 2. Такие силы называют консервативными, например, сила тяжести. Или, иначе, работа консервативной силы по замкнутому пути равна нулю. К числу неконсервативных сил относят, например, силы трения и сопротивления.
То обстоятельство, что работа консервативных сил в случае стационарного поля зависит только от начального и конечного положений частицы, дает возможность ввести важное понятие потенциальной энергии.
Представим себе стационарное поле консервативных сил, в котором будем перемещать частицу из разных точек  в некоторую фиксированную точку
в некоторую фиксированную точку  . Значит, работа сил поля будет некоторой функцией радиус-вектора
. Значит, работа сил поля будет некоторой функцией радиус-вектора  точки
точки  :
:
 (2.12)
(2.12)
Функцию  называют потенциальной энергией частицы в данном поле.
называют потенциальной энергией частицы в данном поле.
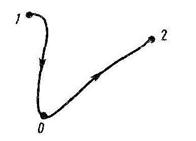 Найдем работу сил поля при перемещении частицы из точки 1 в точку 2 (рисунок 2.1). Так как работа не зависит от пути, выберем путь, проходящий через точку
Найдем работу сил поля при перемещении частицы из точки 1 в точку 2 (рисунок 2.1). Так как работа не зависит от пути, выберем путь, проходящий через точку  . Тогда работа на пути 1
. Тогда работа на пути 1 2 может быть представлена в виде
2 может быть представлена в виде
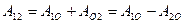 ,
,
или с учетом (11)
Рисунок 2.1  . (2.13)
. (2.13)
Таким образом, работа сил поля на пути 1-2 равна убыли потенциальной энергии частицы в данном поле. Отметим, что потенциальная энергия – функция, определяемая с точностью до прибавления некоторой произвольной постоянной, что несущественно, так как в формулы входит только разность значений  в двух положениях частицы.
в двух положениях частицы.
Потенциальная энергия частицы в поле упругой силы имеет вид  ; в гравитационном (кулоновском) поле материальной точки -
; в гравитационном (кулоновском) поле материальной точки -  ; в однородном поле сил тяжести -
; в однородном поле сил тяжести - 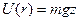 .
.
Закон сохранения механической энергии Согласно выражению (2.11) результирующая 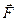 всех сил, действующих на частицу, может быть представлена как сумма:
всех сил, действующих на частицу, может быть представлена как сумма:
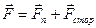 ,
,
где  - консервативная сила, действующая на частицу со стороны силового поля, в котором она находится,
- консервативная сила, действующая на частицу со стороны силового поля, в котором она находится,
 - сторонние силы, не имеющие отношения к данному полю. Работа всех этих сил идет на приращение кинетической энергии частицы:
- сторонние силы, не имеющие отношения к данному полю. Работа всех этих сил идет на приращение кинетической энергии частицы:
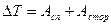 ,
,
где 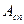 - работа сил поля,
- работа сил поля,  - работа сторонних сил. Согласно (2.13), работа сил поля равна убыли потенциальной энергии частицы:
- работа сторонних сил. Согласно (2.13), работа сил поля равна убыли потенциальной энергии частицы: 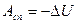 . Получим следующее выражение:
. Получим следующее выражение:
 .
.
Работа сторонних сил идет на приращение величины – суммы кинетической и потенциальной энергий – полной механической энергии частицы в поле:
 .
.
Если 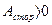 , то полная механическая энергия частицы увеличивается, если
, то полная механическая энергия частицы увеличивается, если 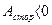 , то уменьшается.
, то уменьшается.
Если сторонние силы отсутствуют или таковы, что не совершают работы в течение интересующего нас времени, то полная механическая энергия частицы в стационарном поле консервативных сил остается постоянной за это время:
 .
.
Экспериментальная часть
Описание экспериментальной установки
 Идея экспериментальной части данной лабораторной работы заключается в использовании законов сохранения движения для решения конкретной практической задачи механики – определение скорости пули.
Идея экспериментальной части данной лабораторной работы заключается в использовании законов сохранения движения для решения конкретной практической задачи механики – определение скорости пули.
Принципиальная схема баллистического маятника показана на рисунке 2.2. Будем предполагать, что движение пули и тела маятника происходит в одной (вертикальной) плоскости. Точкой  обозначена горизонтальная ось, вокруг которой происходит движение маятника. Точка
обозначена горизонтальная ось, вокруг которой происходит движение маятника. Точка 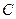 — центр масс тела маятника, имеющего цилиндрическую форму. Для простоты рассмотрения будем считать, что пуля застревает в теле маятника таким образом, что ее центр масс находится на прямой ОС. Размерами пули будем пренебрегать. Существенной особенностью баллистического маятника является то, что время действия силы со стороны пули на маятник (время удара) мало по сравнению с периодом колебания маятника. Такие кратковременные силы, имеющие конечный импульс силы, называются ударными силами, а процесс взаимодействия пули и маятника — ударным процессом. Ударный характер взаимодействия приводит к тому, что к концу удара маятник, приобретя некоторую скорость, практически не успевает отклониться на какую-либо заметную величину.
— центр масс тела маятника, имеющего цилиндрическую форму. Для простоты рассмотрения будем считать, что пуля застревает в теле маятника таким образом, что ее центр масс находится на прямой ОС. Размерами пули будем пренебрегать. Существенной особенностью баллистического маятника является то, что время действия силы со стороны пули на маятник (время удара) мало по сравнению с периодом колебания маятника. Такие кратковременные силы, имеющие конечный импульс силы, называются ударными силами, а процесс взаимодействия пули и маятника — ударным процессом. Ударный характер взаимодействия приводит к тому, что к концу удара маятник, приобретя некоторую скорость, практически не успевает отклониться на какую-либо заметную величину.
При малых временах соударения ударные силы достигают больших значений, так как за малое время действия изменяют импульс тела на заметную величину. Если за время удара на нити не действуют такие большие ударные силы, то для анализа движения цилиндра сразу после удара достаточно учесть лишь силу, действующую со стороны пули. Движение цилиндра при этом можно будет представить, как вращение вокруг мгновенной оси. Но для того, чтобы не возникали ударные силы натяжения нити, необходимо, чтобы такое движение не приводило к изменению длины нитей. А это означает, что мгновенная ось должна совпадать с осью маятника (точка  , рисунок 2.2). Точку пересечения линии действия ударной силы с прямой
, рисунок 2.2). Точку пересечения линии действия ударной силы с прямой в этом случае называют центром удара, а сам удар — центральным ударом.
в этом случае называют центром удара, а сам удар — центральным ударом.
В случае центрального удара натяжения нитей в процессе соударения меняются, так как возникают центростремительные ускорения элементов цилиндра. Однако эти изменения натяжений имеют конечные значения при стремлении времени удара к нулю, поэтому их в процессе соударения можно не учитывать. Если же удар не центральный, то возникают такие ударные натяжения, которые необходимо учитывать при соударении. При этом помимо основного движения возникают высокочастотные колебания, которые довольно быстро затухают.
Обозначим расстояние от точки  до центра масс
до центра масс 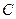 через
через  , а расстояние от точки
, а расстояние от точки  до центра удара — через
до центра удара — через  . Силу, действующую со стороны пули на цилиндр, обозначим через
. Силу, действующую со стороны пули на цилиндр, обозначим через  , момент инерции цилиндра относительно оси, проходящей через центр масс перпендикулярно вертикальной плоскости симметрии,— через
, момент инерции цилиндра относительно оси, проходящей через центр масс перпендикулярно вертикальной плоскости симметрии,— через 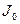 , скорость центра масс цилиндра обозначим через
, скорость центра масс цилиндра обозначим через  , а угловую скорость цилиндра — через
, а угловую скорость цилиндра — через 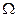 . Пусть удар начинается в момент
. Пусть удар начинается в момент  и заканчивается в момент
и заканчивается в момент  . Учитывая лишь ударную силу
. Учитывая лишь ударную силу  , получим изменение импульса и момента импульса цилиндра относительно оси, проходящей через его центр масс.
, получим изменение импульса и момента импульса цилиндра относительно оси, проходящей через его центр масс.
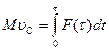 , (2.14)
, (2.14)
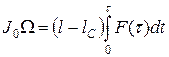 . (2.15)
. (2.15)
В случае центрального удара мгновенная ось совпадает c осью маятника, поэтому
 . (2.16)
. (2.16)
Разделим (2.15) на (2.14) и, учитывая (2.16), получим
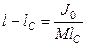 (2.17)
(2.17)
Соотношение (2.17) определяет положение центра удара. Он расположен на расстоянии  от оси
от оси  , т. е. несколько ниже центра масс С.
, т. е. несколько ниже центра масс С.
Рассмотрим изменение импульса пули в результате соударения. Обозначим силу, действующую со стороны цилиндра на пулю, через  , а скорость пули сразу после удара через
, а скорость пули сразу после удара через  . Изменение импульса будет определяться импульсом силы
. Изменение импульса будет определяться импульсом силы
 . (2.18)
. (2.18)
Учитывая третий закон Ньютона 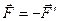 , из сравнения (2.14) и (2.18) получаем соотношение
, из сравнения (2.14) и (2.18) получаем соотношение
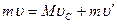 (2.19)
(2.19)
Соотношение (2.19) имеет вид закона сохранения импульса, к которому мы пришли, так как не учитывали действия всех сил, кроме сил  и
и  . Этому соотношению можно придать вид закона сохранения момента импульса. Для этого умножим левую и правую части (2.19) на
. Этому соотношению можно придать вид закона сохранения момента импульса. Для этого умножим левую и правую части (2.19) на  . Учитывая (2.16), (2.17), кинематическое соотношение
. Учитывая (2.16), (2.17), кинематическое соотношение  и вводя момент инерции цилиндра относительно оси
и вводя момент инерции цилиндра относительно оси  :
:
 (2.20)
(2.20)
получим
 . (2.21)
. (2.21)
Заметим, что если бы вместо нитей были жесткие тонкие невесомые стержни с осью в точке  , то соотношение (2.21) выполнялось бы и для нецентрального удара. Но в случае нецентрального удара возникали бы ударные силы, действующие на стержни и, в конечном счете, на ось.
, то соотношение (2.21) выполнялось бы и для нецентрального удара. Но в случае нецентрального удара возникали бы ударные силы, действующие на стержни и, в конечном счете, на ось.
Соотношение (2.19) можно также записать в виде
 (2.22)
(2.22)
После завершения удара маятник будет совершать колебания. При этом максимальное отклонение от положения равновесия пусть будет определяться углом 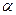 . Если можно пренебречь потерями энергии за четверть периода, то потенциальная энергия маятника в момент остановки будет равна кинетической энергии маятника сразу после удара:
. Если можно пренебречь потерями энергии за четверть периода, то потенциальная энергия маятника в момент остановки будет равна кинетической энергии маятника сразу после удара:
 , (2.23)
, (2.23)
где 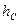 равно изменению высоты центра масс цилиндра при отклонении маятника на угол
равно изменению высоты центра масс цилиндра при отклонении маятника на угол 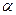 , то есть
, то есть
 (2.24)
(2.24)
Аналогичная формула получается для изменения высоты центра масс пули 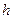 .
.
Учитывая соотношение, связывающее период малых колебаний 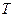 с моментом инерции
с моментом инерции 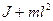
 (2.25)
(2.25)
можно вместо момента инерции 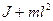 ввести период
ввести период 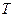 . При этом получим из (2.23) с учетом (2.24)
. При этом получим из (2.23) с учетом (2.24)
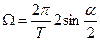 (2.26)
(2.26)
При малых отклонениях 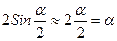 и (2.26) переходит в соотношение, связывающее амплитудные значения скорости
и (2.26) переходит в соотношение, связывающее амплитудные значения скорости 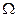 и отклонения
и отклонения 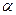 .
.
Из соотношения (2.22) с учетом (2.26) получим
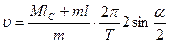 (2.27)
(2.27)
Если  , т. е. размеры цилиндра малы по сравнению с длиной нити, то
, т. е. размеры цилиндра малы по сравнению с длиной нити, то 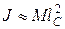 . При этом различием между
. При этом различием между  и
и  в (2.25) можно пренебречь. Вместо (2.25) в таком случае получим
в (2.25) можно пренебречь. Вместо (2.25) в таком случае получим
 (2.28)
(2.28)
Из (2.27) с учетом (2.28), пренебрегая различием между  и
и  , получим
, получим
 (2.29)
(2.29)
Формула (2.29) является окончательной формулой, которая используется в данной работе для определения скорости пули.
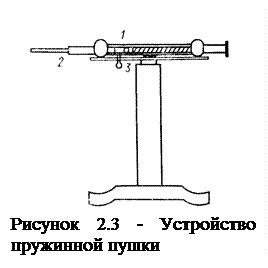
Установка для определения скорости пули состоит из баллистического маятника, шкалы для отсчета отклонений маятника (рисунок 2.2), пружинной пушки (рисунок 2.3) и набора пуль.
 Баллистический маятник представляет собой цилиндр, частично заполненный пластилином и подвешенный в горизонтальном положении на длинных и легких нитях (рисунок 2.2). Масса цилиндра с пластилином равна
Баллистический маятник представляет собой цилиндр, частично заполненный пластилином и подвешенный в горизонтальном положении на длинных и легких нитях (рисунок 2.2). Масса цилиндра с пластилином равна  . В маятник в горизонтальном направлении стреляют из пружинной пушки пулей, имеющей массу
. В маятник в горизонтальном направлении стреляют из пружинной пушки пулей, имеющей массу  и скорость
и скорость  . Пуля входит в пластилин и сообщает маятнику некоторую скорость, в результате чего маятник отклоняется в процессе колебания на некоторый угол, который может быть измерен.
. Пуля входит в пластилин и сообщает маятнику некоторую скорость, в результате чего маятник отклоняется в процессе колебания на некоторый угол, который может быть измерен.
Для того чтобы подготовить пистолет к выстрелу, отводят рычаг 1 (рисунок 2.3) в крайнее положение, сжимая пружину. Вставляют пулю в дуло пистолета 2 и задвигают ее шомполом до конца. Убедившись в том, что пуля, вылетевшая из пистолета, может попасть лишь в маятник, производят выстрел. Для этого курок 3 отводят вертикально вниз. Делают отсчет отклонения маятника, по шкале.
Проведение эксперимента
Прежде всего необходимо убедиться в том, что ось цилиндра в положении равновесия горизонтальна, а вертикальная плоскость, проходящая через ось цилиндра, является плоскостью симметрии. Если эти условия не выполнены, то необходимо подрегулировать длину нитей.
Шкалу, предназначенную для определения отклонения маятника, устанавливают параллельно отсчетной рамке маятника на расстоянии примерно 5-6 мм от нее. Угол отклонения маятника 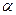 определяется по смещению
определяется по смещению  нити отсчетной рамки в горизонтальном направлении, исходя из условия
нити отсчетной рамки в горизонтальном направлении, исходя из условия
 (2.30)
(2.30)
где 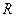 — расстояние от оси маятника до горизонтальной линии шкалы, вдоль которой измеряется смещение нити рамки. При малых углах можно считать, что
— расстояние от оси маятника до горизонтальной линии шкалы, вдоль которой измеряется смещение нити рамки. При малых углах можно считать, что 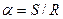 .
.
Измерения
1 Определить массу пули с помощью весов. Результаты занести в таблицу 2.1.
2 Произвести выстрелы последовательно с каждой из трех пуль. Результаты отсчета отклонений маятника записать в таблицу 2.1. Для каждой пули необходимо произвести не менее пяти выстрелов и соответственно этому не менее пяти отсчетов отклонения маятника.
Таблица 2.1
| пуля | № опыта | S | <S>,sS | a, 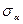
| υ, 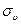
|
| m1= | |||||
| … | |||||
| …… |
Обработка результатов
1 Определить среднее значение отклонения <S> и стандартное отклонение от среднего sS.
2 По формуле (2.30) для каждой пули найти величину 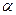 и ее стандартное отклонение. Данные занести в таблицу 2.1.
и ее стандартное отклонение. Данные занести в таблицу 2.1.
3 По формуле (2.29) вычислить значение скорости пули и ее стандартное отклонение. Используемые в (2.29) масса цилиндра и расстояние от оси О до центра масс цилиндра даются преподавателем.
Основные итоги работы
В результате выполнения работы должны быть определены скорости пуль (не менее трех) разной массы.
Контрольные вопросы
1 С какими свойствами пространства и времени связаны законы сохранения импульса, механической энергии и момента импульса?
2 Импульс частицы и системы частиц: определение, формула, направление, единицы измерения.
3 Сформулируйте закон сохранения импульса.
4 Механическая работа: определение, формула, единицы измерения. Физический и геометрический смысл механической работы силы.
5 Получите связь между работой результирующей всех сил и приращением кинетической энергии.
6 Механическая мощность: определение, формула, единицы измерения. Что такое «лошадиная сила»?
7 Какие силы называют консервативными? Докажите, что сила тяжести – консервативная сила и работа силы тяжести не зависит от формы траектории, а зависит от начального и конечного положения тела или частицы.
8 Покажите, что работа консервативной силы по замкнутому пути равна нулю.
9 Пользуясь выражением (2.12), получите потенциальную энергию частицы в поле упругой силы, в однородном поле сил тяжести и в гравитационном поле материальной точки.
10 Сформулируйте закон сохранения механической энергии.
11 Получите расчетную формулу для вычисления скорости пули методом баллистического маятника.
Рекомендуемая литература
2.4.1 Иродов, И.Е. Механика. Основные законы механики / И.Е.Иродов. - М.: Бином, 2009. – 310 с. - ISBN 978-5-9963-0063-1.
2.4.2 Савельев, И.В. Курс общей физики: в 5 кн. / И.В.Савельев. – М.: АСТРЕЛЬ: АСТ, 2005. – Кн. 1: Механика. – 336 с. - ISBN 5-271-01034-1.
2.4.3 Сивухин, Д.В. Общий курс физики: в 3 т. / Д.В.Сивухин. - М.: Физматлит, 2002. – Т. 1: Механика. – 560 с. - ISBN 5-89155-078-4.
2.4.4 Трофимова, Т.И. Физика в таблицах и формулах / Т.И. Трофимова. – М.: Академия, 2006. – 448 с. - ISBN 5-7695-2277-1.
Лабораторная работа №3. Маятники
Цель работы:1) изучение кинематики и динамики гармонического колебательного движения.
2) изучение физического маятника.
3) измерение ускорения свободного падения  при помощи оборотного маятника (метод Бесселя).
при помощи оборотного маятника (метод Бесселя).
Теоретическая часть
Колебаниями называются процессы, отличающиеся той или иной степенью повторяемости. Таким свойством повторяемости обладают, например, качания маятника часов, колебания струны или ножек камертона, напряжение между обкладками конденсатора в контуре радиоприемника и т.п.
В зависимости от физической природы повторяющегося процесса различают колебания: механические, электромагнитные, электромеханические и т.д. В данной работе рассматриваются механические колебания.
Колебания широко распространены в природе и технике. Во многих случаях они играют отрицательную роль. Колебания моста, возникающие из-за толчков, сообщаемых ему колесами поезда при прохождении через стыки рельсов, колебания (вибрации) корпуса корабля, вызванные вращением гребного винта – все эти процессы могут привести к катастрофическим последствиям. В подобных случаях задача заключается в том, чтобы предотвратить возникновение колебаний или во всяком случае воспрепятствовать тому, чтобы колебания достигли опасных размеров.
Вместе с тем колебательные процессы лежат в самой основе различных отраслей техники. Так, например, на колебательных процессах основана вся радиотехника.
В зависимости от характера воздействия на систему различают свободные (или собственные) колебания, вынужденные колебания, автоколебания и параметрические колебания.
Свободными, или собственными, называются такие колебания, которые происходят в системе, предоставленной самой себе после того, как ей был сообщен толчок или она была выведена из положения равновесия. Примером могут служить колебания шарика, подвешенного на нити. Для того, чтобы вызвать колебания, можно либо толкнуть шарик, либо, отведя в сторону, отпустить его.
Вынужденными называются такие колебания, в процессе которых колеблющаяся система подвергается воздействию внешней периодически изменяющейся силы. Примером служат колебания моста, возникающие при прохождении по нему людей, шагающих в ногу.
Автоколебания, как и вынужденные колебания, сопровождаются воздействием на колеблющуюся систему внешних сил, однако моменты времени, когда осуществляются эти воздействия, задаются самой колеблющейся системой – система сама управляет внешним воздействием. Примером автоколебательной системы являются часы, в которых маятник получает толчки за счет энергии поднятой гири или закрученной пружины, причем эти толчки происходят в моменты прохождения маятника через среднее положение. При параметрических колебаниях за счет внешнего воздействия происходит периодическое изменение какого-либо параметра системы, например, длины нити, к которой подвешен шарик, совершающий колебания.
Важнейшим среди колебательных движений является так называемое простое или гармоническое колебательное движение. Гармоническими называют колебания, в которых интересующая нас величина 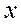 (например, линейное или угловое смещение из положения равновесия) изменяется со временем
(например, линейное или угловое смещение из положения равновесия) изменяется со временем  по закону
по закону
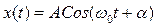 , (3.1)
, (3.1)
где  – амплитуда,
– амплитуда,  - фаза,
- фаза, 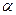 – начальная фаза,
– начальная фаза,  – циклическая (круговая) частота колебаний. Эта частота связана с периодом
– циклическая (круговая) частота колебаний. Эта частота связана с периодом 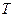 (время одного полного колебания) и линейной частотой (число колебаний в единицу времени)
(время одного полного колебания) и линейной частотой (число колебаний в единицу времени)  как
как
 . (3.2)
. (3.2)
Обратим внимание на различие наименований циклической и линейной частот:  .
.
Продифференцировав (1) по времени, найдем скорость и ускорение:
 (3.3), (3.4)
(3.3), (3.4)
Из этих выражений видно, что скорость и ускорение также изменяются по гармоническому закону с амплитудами  и
и 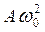 соответственно. При этом скорость опережает смещение
соответственно. При этом скорость опережает смещение 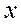 по фазе на
по фазе на  , а ускорение – на
, а ускорение – на  , т.е. в противофазе со смещением. На рисунке 3.1 приведены графики зависимостей
, т.е. в противофазе со смещением. На рисунке 3.1 приведены графики зависимостей 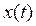 ,
, 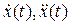 для случая
для случая 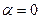 .
.
 Сопоставив (3.1) и (3.4), видим, что
Сопоставив (3.1) и (3.4), видим, что 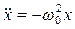 , или
, или
 . (3.5)
. (3.5)
Это дифференциальное уравнение второго порядка называют уравнением гармонического осциллятора. Его решение[2] содержит две произвольные постоянные:  и
и 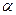 .
.
Рисунок 3.1
Для каждого конкретного колебания они определяются начальными условиями – смещением  и скоростью
и скоростью 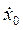 в начальный момент
в начальный момент  :
:
 (3.6)
(3.6)
Отсюда находим искомые постоянные:
 (3.7)
(3.7)
Обычно рассматривают только значения 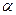 в интервале (-π, +π). Уравнение для
в интервале (-π, +π). Уравнение для 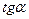 удовлетворяется двумя значениями
удовлетворяется двумя значениями 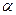 в этом интервале. Из этих значений следует взять то, при котором получаются правильные знаки у
в этом интервале. Из этих значений следует взять то, при котором получаются правильные знаки у 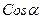 и
и 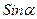 в (3.6).
в (3.6).
Простейшей колебательной системой является маятник, например, математический, пружинный или физический. Маятник – это твердое тело, совершающее под действием приложенных к нему сил, колебания около неподвижной точки или оси.
Математический маятник – система из упругой и нерастяжимой нити длиной l и тела массой m, размеры которого малы по сравнению с длиной нити (рисунок 3.2).

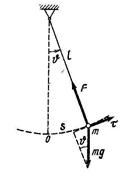
Рисунок 3.2 - Математический маятник Рисунок 3.3 - Пружинный маятник
 Имея в виду, что
Имея в виду, что 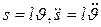 и что проекция силы натяжения
и что проекция силы натяжения 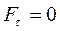 , запишем:
, запишем: 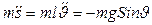 , или
, или
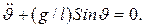
Из сопоставления с (3.5) видим, что это уравнение, вообще говоря, не является уравнением гармонического осциллятора, поскольку в нем вместо смещения  стоит
стоит  . Однако при малых колебаниях,
. Однако при малых колебаниях,
Рисунок 3.4 Физический маятник
когда  , уравнение совпадает с (3.5):
, уравнение совпадает с (3.5):
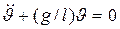 ,
,
Откуда следует, что частота  и период
и период 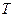 математического маятника, совершающего малые колебания, равны
математического маятника, совершающего малые колебания, равны
 (3.8)
(3.8)
Пружинный маятник – система из пружины жесткостью 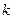 и твердого тела массой
и твердого тела массой 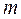 (рисунок 3.3). Пусть грузик массы
(рисунок 3.3). Пусть грузик массы  , подвешенный на невесомой пружине жесткости
, подвешенный на невесомой пружине жесткости 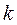 , совершает вертикальные колебания. Возьмем начало О оси
, совершает вертикальные колебания. Возьмем начало О оси 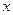 в положении равновесия, где
в положении равновесия, где 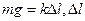 – растяжение пружины в этом положении. Тогда, согласно основному уравнению динамики,
– растяжение пружины в этом положении. Тогда, согласно основному уравнению динамики,  , или
, или

Из сопоставления с (3.5) видим, что это уравнение гармонического осциллятора, колеблющегося около положения равновесия с частотой  и периодом
и периодом 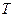 , равными
, равными
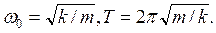 (3.9)
(3.9)
Физическим маятником называется твердое тело, которое может качаться вокруг неподвижной горизонтальной оси, жестко связанной с телом. Рассмотрим колебания под действием силы тяжести (рисунок 3.4). Выберем положительное направление отсчета угла 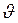 против часовой стрелки (ось
против часовой стрелки (ось 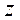 направлена к нам). Тогда проекция момента силы тяжести на ось
направлена к нам). Тогда проекция момента силы тяжести на ось  запишется как
запишется как  и уравнение динамики вращательного движения твердого тела примет вид
и уравнение динамики вращательного движения твердого тела примет вид
 ,
,
где 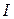 - момент инерции тела относительно оси
- момент инерции тела относительно оси  ,
,
 - расстояние между осью
- расстояние между осью  (точка
(точка  ) и центром масс
) и центром масс 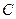 . При малых колебаниях
. При малых колебаниях 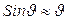 . При этом условии предыдущее уравнение можно записать так:
. При этом условии предыдущее уравнение можно записать так:
 .
.
Колебания будут гармоническими с частотой  и периодом
и периодом 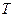 , равными
, равными
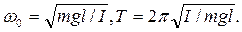 (3.10)
(3.10)
Такую же частоту и период имеет математический маятник длины
 ,
,
которую называют приведенной длиной физического маятника.
Точку  (рисунок 3.4), которая находится на прямой, проходящей через точку подвеса
(рисунок 3.4), которая находится на прямой, проходящей через точку подвеса  и центр масс
и центр масс 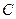 , и отстоит от точки
, и отстоит от точки  на расстоянии
на расстоянии  , называют центром качания физического маятника. Центр качания
, называют центром качания физического маятника. Центр качания  обладает замечательным свойством: если маятник перевернуть и заставить совершать малые колебания вокруг оси
обладает замечательным свойством: если маятник перевернуть и заставить совершать малые колебания вокруг оси  , то период колебаний не изменится. На этом свойстве основано определение ускорения свободного падения с помощью оборотного маятника: экспериментально устанавливают положения двух «сопряженных» точек (осей)
, то период колебаний не изменится. На этом свойстве основано определение ускорения свободного падения с помощью оборотного маятника: экспериментально устанавливают положения двух «сопряженных» точек (осей) 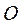 и
и  , малые колебания вокруг которых происходят с одинаковой частотой. Это значит, что расстояние
, малые колебания вокруг которых происходят с одинаковой частотой. Это значит, что расстояние 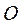
 =
= . Определив
. Определив  и
и  , из формулы
, из формулы  находим
находим  . Что и предлагается сделать в экспериментальной части работы.
. Что и предлагается сделать в экспериментальной части работы.
Рассмотренные примеры относятся к свободным колебаниям без трения. Можно утверждать, что свободные колебания любого осциллятора в отсутствие трения будут гармоническими, если действующая в нем сила (или момент силы) является квазиупругой, т.е. силой, направленной к положению равновесия и зависящей от смещения из этого положения линейно. Именно квазиупругий характер силы (или момента силы) служит и критерием малых колебаний. Кроме того, частота и период свободных колебаний без трения зависят только от свойств самого осциллятора в отличие от амплитуды и начальной фазы, которые определяются начальными условиями.
Энергия гармонического осциллятора. Рассмотрим этот вопрос на примере материальной точки массы  , колеблющейся под действием квазиупругой силы
, колеблющейся под действием квазиупругой силы 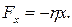 Потенциальная и кинетическая энергии частицы имеют в данном случае такой вид:
Потенциальная и кинетическая энергии частицы имеют в данном случае такой вид:
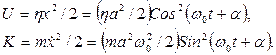 (3.11)
(3.11)
Из этих соотношений видно, что значения  и
и 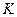 сдвинуты друг относительно друга по фазе на
сдвинуты друг относительно друга по фазе на  : когда
: когда  максимальна,
максимальна, 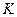 минимальна, и наоборот. При этом полная энергия сохраняется:
минимальна, и наоборот. При этом полная энергия сохраняется:
 (3.12)
(3.12)
где учтено, что 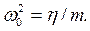 Принимая во внимание (3.12), формулы (3.11) можно переписать так:
Принимая во внимание (3.12), формулы (3.11) можно переписать так:

Графики зависимостей 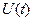 и
и 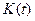 даны на рисунке 3.5. Из рисунка видно, что в процессе колебаний происходит переход потенциальной энергии в кинетическую и обратно. Это иллюстрирует и рисунок 3.6.
даны на рисунке 3.5. Из рисунка видно, что в процессе колебаний происходит переход потенциальной энергии в кинетическую и обратно. Это иллюстрирует и рисунок 3.6.

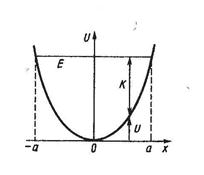
Рисунок 3.5 Рисунок 3.6
Экспериментальная часть
Измерение периода колебаний любого физического маятника позволяет в принципе определить ускорение свободного падения g в любой точке земного шара. Эти методы определения g известны и используются в гравиметрии. Маятниковые гравиметрические приборы удобны для определения вариаций g, т.е. нахождения отношений значений g в различных точках поля тяготения, однако их точность уступает другим типам гравиметров. Часто маятниковые приборы используются для решения более сложной задачи — определения абсолютного значения g. В этом случае измерения проводятся таким образом, чтобы исключать из окончательных формул величину момента инерции маятника.
Если амплитуда колебаний маятника мала, например, не более 3–4°, то период колебаний определяется формулой (3.10):
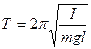 .
.
Используя теорему Гюйгенса–Штейнера
 ,
,
где  — момент инерции маятника относительно оси, проходящей через центр масс и параллельной оси подвеса, представим выражение (3.10) для периода колебаний маятника в следующем виде:
— момент инерции маятника относительно оси, проходящей через центр масс и параллельной оси подвеса, представим выражение (3.10) для периода колебаний маятника в следующем виде:
 .
.
Предположим, что мы определили периоды колебаний маятника, подвешивая его в двух разных точках, находящихся на расстояниях 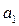 и
и  от центра масс. Из уравнений
от центра масс. Из уравнений
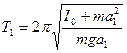 ,
, 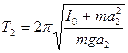
получаем

откуда
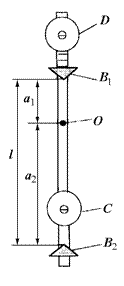
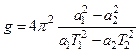 .
.
Используя несложные преобразования, для величины g можно также получить формулу, данную Бесселем:
 , (3.13)
, (3.13)
где 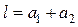 .
.
Если периоды равны между собой (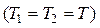 [3]), то
[3]), то
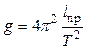 , (3.14)
, (3.14)
Рисунок 3.7 - Устройство где  - приведенная длина маятника.
- приведенная длина маятника.
оборотного маятника
Описание экспериментальной установки
В данной работе используется оборотный маятник, изображенный на рисунке 3.7. На металлическом стержне опорные призмы B1 и B2 жестко закреплены и не перемещаются. Расстояние между ними l фиксировано и его значение либо задано, либо измеряется в начале эксперимента.
Также фиксировано и положение чечевицы C. Вторая чечевица D находится на конце стержня (не между призмами) и может перемещаться по нему, причем ее положение определяется по шкале сквозь прозрачный глазок на чечевице (расстояние между рисками шкалы на стержне 10 мм). Центр масс[4] маятника на схеме обозначен точкой О.
Период колебаний определяется секундомером. Для более точного определения периода колебаний, секундомером измеряется время не одного, а двадцати (или сотни) периодов колебаний.
Проведение эксперимента
Измерения и обработка результатов
1 Подвесьте маятник на призме B1 (прямое положение маятника) и закрепите чечевицу D в ближайшем к призме B1 положении, соответствующем совмещению риски глазка чечевицы с одной из поперечных рисок на стержне, это положение чечевицы D, - x, примем за 0 и от него будем измерять другие положения чечевицы D.
2 Отклоните маятник от положения равновесия на 5° (нижний конец стержня — на 5 см от вертикали) и измерьте время Tn, за которое происходят n периодов колебаний, где  при измерении времени секундомером или n =5–10 раз при измерении с помощью таймера. Проделайте измерения времени 3 раза и результаты занесите в таблицу 3.1.
при измерении времени секундомером или n =5–10 раз при измерении с помощью таймера. Проделайте измерения времени 3 раза и результаты занесите в таблицу 3.1.
Таблица 3.1
| Положение чечевицы D, х мм | Прямое положение маятника (на призме B1) | Обратное положение маятника (на призме B2) | ||||||
| n |  , с , с
|  , с , с
| T1, c | n |  , с , с
|  , с , с
| T2, c | |
| xmax | ||||||||
| x1 | ||||||||
| x2 | ||||||||
| x3 | ||||||||
3 Перевернув маятник и подвесив его на призме B2 (обратное положение маятника), повторите измерения по п. 2. Результаты также занесите в таблицу 3.1.
4 Измените положение чечевицы D на максимально возможное[5], повторите измерения по п. 2 и п.3. Результаты также занесите в таблицу 3.1.
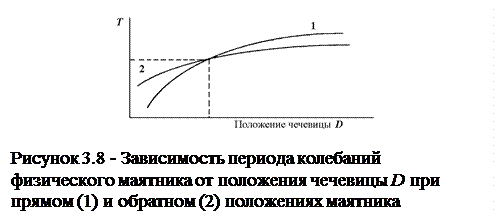 |
5 Обратите внимание на то, что первом измерении ( x1=0 ) Т1 было меньше Т2 а во втором ( х2= xmax ) - Т1 больше Т2. Типичный вид зависимости периодов T1 и T2 от координаты чечевицы D . показан на рисунке 3.8. Чтобы можно было пользоваться простой формулой (3.14), необходимо найти такое положение чечевицы D, при котором периоды T1 = T2 = T (точка пересечения графиков). При этом lпр будет равна расстоянию между призмами. Эту точку можно найти, многократно повторив измерения по п.1, каждый раз увеличивая x (положение чечевицы D) на 1 см и затем построив зависимости T1 и T2 от x.
Другой способ — итерационный. Проведя измерения в точках x1, x2 находящихся с разных сторон от точки пересечения графиков, приближенное положение этой точки следует вычислить по формуле:

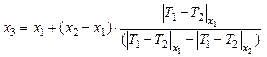 (3.15)
(3.15)
Установите чечевицу в положение x3 и повторите измерения по п. 2 и п. 3. Результаты занесите в таблицу 3.1.
6 Если точка x3 оказалась слева от точки пересечения графиков рассчитайте x4 по формуле (3.15), заменив в ней x1 на x3. Если же точка x3 оказалась справа от точки пересечения графиков рассчитайте x4 по формуле (3.15), заменив в ней x2 на x3. Проведите измерения для нового положения чечевицы x4. Результаты занесите в таблицу 3.1.
7 Если периоды колебаний в точке различаются на величину, превышающую ошибку измерения периода, проделайте еще одну итерацию по п.6.
8 По графику рисунка 3.8 определите ординату пересечения кривых 1 и 2, соответствующую искомому значению величины T, вычислите значение g по формуле (3.14).
9 Оцените погрешность проведенных косвенных измерений величины g, вычисленной по формуле (3.14)[6]:
 ,
,
где абсолютную погрешность 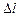 примите равной 0,5 мм (половине цены деления используемой миллиметровой линейки),
примите равной 0,5 мм (половине цены деления используемой миллиметровой линейки),
абсолютную погрешность  примите равной 0,01 с.
примите равной 0,01 с.
10 Для увеличения точности определения ускорения свободного падения проведите измерения при найденном положении чечевицы аналогично п. 2 для прямого и обратного положений маятника, но измеряйте время ста или двухсот периодов колебаний. Результаты занесите в таблицу 3.2.
11 Рассчитайте значения периодов T1 и T2 и оцените погрешности их определения. Данные занесите в таблицу 3.2.
Таблица 3.2
| Номер опыта | Прямое положение маятника (на призме B1) | Обратное положение маятника (на призме B2) | ||||||
| n |  , с , с
|  , с , с
| T1, 
| n |  , с , с
|  , с , с
| T2, 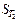
| |
| 100- -200 | 100- -200 | |||||||
12 Если не удалось найти положения чечевицы, при котором периоды T1 и T2 равны, следует определить а1 и а2. Для определения величин а1 и а2 снимите маятник с подвеса, проденьте его в петлю из нити, подвешенной на подвесе и найдите центр масс маятника (центр масс будет совпадать с положением нити, когда вы добьётесь равновесия и стержень маятника будет располагаться горизонтально).
При помощи линейки измерьте расстояния а1 и а2 от центра масс до призм B1 и B2. Повторите измерения три раза, результаты занесите в таблицу 3.3.
Таблица 3.3
| Номер опыта | 
| 
| 
| 
| 
| 
|
13 Определите средние значения a1 и a2, а также их стандартные отклонения. Данные занесите в таблицу 3.3.
14 Сравните полученный в п. 8 и 9 результат с табличным (справочным) значением g: gтеор=(9.81±0,01 )м/с2.
15 Определите величину g по формуле (3.13), используя данные таблиц 3.2 и 3.3.
16 Сравните результат вычислений по формуле (3.13) с результатом, полученным по упрощенной формуле (3.14).
Основные итоги работы
В результате выполнения работы должно быть получено значение ускорения свободного падения, проведено сравнение с табличным значением и проанализированы причины, приводящие к увеличению погрешности эксперимента.
Контрольные вопросы
1 Что такое колебание? Перечислите виды колебаний по способу возбуждения колебательной системы и приведите примеры.
2 Гармоническое колебание: уравнение, график, кинематические, динамические, энергетические превращения в гармоническом осцилляторе.
3 Математический маятник. Вывод формулы для периода колебаний математического маятника.
4 Пружинный маятник. Вывод формулы для периода колебаний пружинного маятника.
5 Получите формулу для периода пружинного маятника, состоящего из грузика массой 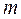 и двух пружин, соединенных параллельно, жесткостью
и двух пружин, соединенных параллельно, жесткостью 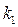 и
и  .
.
6 Получите формулу для периода пружинного маятника, состоящего из грузика массой 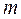 и двух пружин, соединенных последовательно, жесткостью
и двух пружин, соединенных последовательно, жесткостью 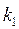 и
и 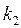 .
.
7 Физический маятник. Вывод формулы для периода колебаний физического маятника.
8 Что называется приведенной длиной физического маятника? Напишите формулу для приведенной длины.
9 Что такое квазиупругая сила? При каких условиях маятник совершает гармонические колебания?
10 Сформулируйте теорему Гюйгенса–Штейнера.
11 Дайте вывод упрощенной формулы (3.13) для расчета ускорения свободного падения.
12 По каким причинам ускорение свободного падения зависит от высоты над уровнем моря, а также от географической широты?
13 Если частица совершает гармонические колебания с амплитудой A, то, какое расстояние она проходит за один период?
14 Если маятниковые часы идут точно на уровне моря, то будут ли они спешить или отставать, если их поднять на высокую гору?
3.4 Рекомендуемая литература
3.4.1 Зисман, Г.А. Курс общей физики: в 3 т. / Г.А. Зисман, О.М. Тодес. – СПб.: Лань, 2007. – Т.1: Механика. Молекулярная физика. Колебания и волны. – 340 с. - ISBN 978-5-8114-0753-8.
3.4.2 Иродов, И.Е. Механика. Основные законы механики / И.Е.Иродов. - М.: Бином, 2009. – 310 с. - ISBN 978-5-9963-0063-1.
3.4.3 Савельев, И.В. Курс общей физики: в 5 кн. / И.В.Савельев. – М.: АСТРЕЛЬ: АСТ, 2005. – Кн. 1: Механика. – 336 с. - ISBN 5-271-01034-1.
3.4.4 Сивухин, Д.В. Общий курс физики: в 3 т. / Д.В.Сивухин. - М.: Физматлит, 2002. – Т. 1: Механика. – 560 с. - ISBN 5-89155-078-4.
3.4.5 Трофимова, Т.И. Физика в таблицах и формулах / Т.И. Трофимова. – М.: Академия, 2006. – 448 с. - ISBN 5-7695-2277-1.
Лабораторная работа №4. Основное уравнение динамики вращательного движения
Цель работы:1) изучение кинематики вращательного движения.
2) изучение динамики вращательного движения.
3) экспериментальная проверка основного уравнения вращательного движения твердого тела вокруг закрепленной оси.
Теоретическая часть
Твердым телом в механике называют неизменяемую систему материальных точек, т.е. такую идеализированную систему, при любых движениях которой взаимные расстояния между материальными точками системы остаются неизменными. Здесь, как и вообще в классической механике, под материальными точками понимают не атомы и молекулы, а достаточно малые макроскопические части, на которые мысленно можно разделить рассматриваемую механическую систему.
Различают пять видов движения твердого тела: 1) поступательное, 2) вращение вокруг неподвижной оси, 3) плоское движение, 4) движение вокруг неподвижной точки и 5) свободное движение. Первые два движения (поступательное и вращение вокруг неподвижной оси) являются основными движениями твердого тела. Остальные виды движения твердого тела, оказывается, можно свести к одному из основных движений или к их совокупности.
При поступательном движении все точки тела совершают за один и тот же промежуток времени равные перемещения. Поэтому скорости и ускорения всех точек тела в данный момент времени одинаковы. Это обстоятельство позволяет свести изучение поступательного движения твердого тела к изучению движения отдельной точки тела, т.е. к задаче кинематики точки. Таким образом, поступательное движение твердого тела может быть полностью описано, если известны зависимость от времени радиуса-вектора 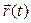 любой точки этого тела и положение последнего в начальный момент.
любой точки этого тела и положение последнего в начальный момент.
При вращательном движении все точки твердого тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Для описания вращательного движения нужно задать положение в пространстве оси вращения и угловую скорость тела в каждый момент времени.
 Вращение вокруг неподвижной оси. Пусть твердое тело, вращаясь вокруг неподвижной в данной системе отсчета оси
Вращение вокруг неподвижной оси. Пусть твердое тело, вращаясь вокруг неподвижной в данной системе отсчета оси  , совершило за время
, совершило за время  бесконечно малый поворот. Соответствующий угол поворота будем характеризовать вектором
бесконечно малый поворот. Соответствующий угол поворота будем характеризовать вектором 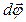 , модуль которого равен углу поворота, а направление совпадает с осью
, модуль которого равен углу поворота, а направление совпадает с осью  , причем так, что направление поворота отвечает правилу правого винта по отношению к направлению вектора
, причем так, что направление поворота отвечает правилу правого винта по отношению к направлению вектора 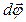 (рисунок 4.1).
(рисунок 4.1).
Рисунок 4.1
Положение точки А можно задать радиусом-вектором  , проведенным из некоторой точки
, проведенным из некоторой точки  на оси вращения. Тогда линейное перемещение конца радиуса-вектора
на оси вращения. Тогда линейное перемещение конца радиуса-вектора  (рисунок 4.1) связано с углом поворота
(рисунок 4.1) связано с углом поворота 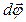 соотношением
соотношением
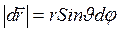 , или в векторном виде
, или в векторном виде
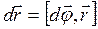 . (4.1)
. (4.1)
Отметим, что это равенство справедливо лишь для бесконечно малого поворота 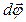 .
.
Вектор угловой скорости определяют как
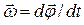 , (4.2)
, (4.2)
где  - промежуток времени, за который тело совершает поворот
- промежуток времени, за который тело совершает поворот  . Вектор
. Вектор  совпадает по направлению с вектором
совпадает по направлению с вектором  .
.
Изменение вектора  со временем характеризуют вектором углового ускорения
со временем характеризуют вектором углового ускорения 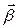 :
:
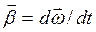 . (4.3)
. (4.3)
Направление вектора 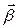 совпадает с направлением
совпадает с направлением  - приращения вектора
- приращения вектора  .
.
Вектора  ,
,  и
и 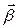 , направление которых связано с направлением оси вращения, называют аксиальными.
, направление которых связано с направлением оси вращения, называют аксиальными.
Единицей угловой скорости в СИ является радиан в секунду (рад/с), а единицей углового ускорения – радиан на секунду в квадрате (рад/с2).
Выражения для угловой скорости и углового ускорения в проекции на ось вращения  имеют следующий вид:
имеют следующий вид:
 (4.4)
(4.4)
Таким образом, зная зависимость 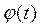 - закон вращения тела, по формулам (4.4) можно найти угловую скорость и угловое ускорение в каждый момент времени. И наоборот, если известны зависимость углового ускорения от времени и начальные условия, т.е. угловая скорость
- закон вращения тела, по формулам (4.4) можно найти угловую скорость и угловое ускорение в каждый момент времени. И наоборот, если известны зависимость углового ускорения от времени и начальные условия, т.е. угловая скорость 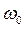 и угол
и угол 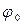 в начальный момент времени, то можно найти
в начальный момент времени, то можно найти 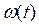 и
и 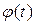 .
.
Связь между линейными и угловыми величинами. Рассмотрим точку А, положение которой относительно некоторой точки  оси вращения характеризуется радиусом-вектором
оси вращения характеризуется радиусом-вектором  (рисунок 4.2).
(рисунок 4.2).
Если формулу (4.1) поделить на соответствующий промежуток времени  и учесть, что
и учесть, что 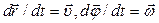 , то
, то
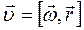 , (4.5)
, (4.5)
т.е. скорость 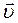 любой точки А твердого тела, вращающегося вокруг некоторой оси с угловой скоростью
любой точки А твердого тела, вращающегося вокруг некоторой оси с угловой скоростью  , равна векторному произведению
, равна векторному произведению  на радиус-вектор
на радиус-вектор  точки А относительно произвольной точки
точки А относительно произвольной точки  оси вращения.
оси вращения.
Модуль вектора (4.5) 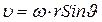 , или
, или
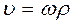 ,
,
где 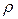 - радиус окружности, по которой движется точка А.
- радиус окружности, по которой движется точка А.
 Продифференцировав (4.5) по времени, можно найти полное ускорение точки А:
Продифференцировав (4.5) по времени, можно найти полное ускорение точки А: 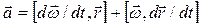 , или
, или
 (4.6)
(4.6)
В данном случае (ось вращения неподвижна)  , поэтому вектор
, поэтому вектор  представляет собой тангенциальное ускорение
представляет собой тангенциальное ускорение 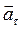 . Вектор же
. Вектор же 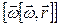 - это нормальное ускорение
- это нормальное ускорение 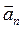 . Проекции вектора
. Проекции вектора 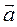 на орты
на орты  равны:
равны:

Рисунок 4.2 Отсюда модуль полного ускорения

Динамика вращательного движения. Важные законы механики связаны с понятиями момента импульса и момента силы. Однако следует различать моменты этих векторов относительно точки и относительно оси. Момент вектора относительно точки есть вектор. Момент того же вектора относительно оси есть проекция на эту ось его момента относительно точки, лежащей на той же оси.
Пусть  - какая-либо точка, относительно которой рассматривается момент вектора силы,
- какая-либо точка, относительно которой рассматривается момент вектора силы,  - радиус-вектор, проведенный из этой точки к точке приложения силы
- радиус-вектор, проведенный из этой точки к точке приложения силы 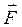 (рисунок 4.3).
(рисунок 4.3).
Моментом силы 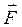 относительно точки
относительно точки  называется векторное произведение радиуса-
называется векторное произведение радиуса-
Рисунок 4.3
вектора  на силу
на силу 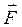 :
:
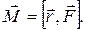 . (4.7)
. (4.7)
Из этого определения следует, что момент 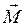 не изменится, если точку приложения силы
не изменится, если точку приложения силы 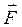 перенести в любую другую точку, расположенную на линии действия силы.
перенести в любую другую точку, расположенную на линии действия силы.  .
.
Моментом 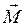 нескольких сил относительно точки называется сумма моментов этих сил относительно той же точки. Если линии действия сил
нескольких сил относительно точки называется сумма моментов этих сил относительно той же точки. Если линии действия сил  лежат в одной плоскости, то момент всех действующих сил относительно некоторой точки равен моменту их равнодействующей силы относительно той же точки:
лежат в одной плоскости, то момент всех действующих сил относительно некоторой точки равен моменту их равнодействующей силы относительно той же точки:
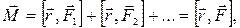 (4.8)
(4.8)
где  - геометрическая сумма сил
- геометрическая сумма сил  , называемая их равнодействующей.
, называемая их равнодействующей.
Отметим частный случай двух равных параллельных сил 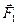 и
и  , направленных в противоположные стороны (пара сил):
, направленных в противоположные стороны (пара сил):
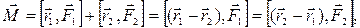
т.е. момент пары сил равен моменту одной из этих сил относительно точки приложения другой.
 Для определения аналитического выражения момента силы относительно оси надо найти проекцию на ось векторного произведения
Для определения аналитического выражения момента силы относительно оси надо найти проекцию на ось векторного произведения  . Воспользуемся цилиндрической системой координат
. Воспользуемся цилиндрической системой координат  , связав с частицей а (рисунок 4.4) орты
, связав с частицей а (рисунок 4.4) орты  направленные в сторону возрастания соответствующих координат.
направленные в сторону возрастания соответствующих координат.
В этой системе координат радиус-вектор  и сила
и сила 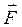 , действующая на частицу, записываются так:
, действующая на частицу, записываются так:
Рисунок 4.4 
 ,
,
где 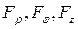 - проекции вектора
- проекции вектора 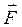 на соответствующие орты. Из векторной алгебры известно, что векторное произведение
на соответствующие орты. Из векторной алгебры известно, что векторное произведение  можно представить определителем
можно представить определителем
 ,
,
откуда сразу видно, что момент силы относительно оси 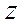
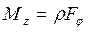 . (4.9)
. (4.9)
Аналогом массы во вращательном движении является момент инерции. Моментом инерции материальной точки относительно оси вращения называется произведение массы материальной точки на квадрат расстояния ее до оси вращения:
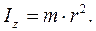 (4.10)
(4.10)
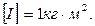 Момент инерции – величина скалярная и аддитивная, поэтому момент инерции системы материальных точек относительно оси
Момент инерции – величина скалярная и аддитивная, поэтому момент инерции системы материальных точек относительно оси 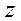 :
:
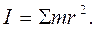 (4.11)
(4.11)
Момент инерции твердого тела зависит от распределения масс относительно данной оси и вычисляется по формуле:
 (4.12)
(4.12)
где  и
и 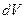 - масса и объем элемента тела, находящегося на расстоянии
- масса и объем элемента тела, находящегося на расстоянии 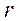 от оси
от оси 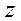 ,
,
 - плотность тела в данной точке.
- плотность тела в данной точке.
Моменты инерции некоторых однородных твердых тел относительно оси 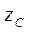 , проходящей через центр масс тела, приведены в следующей таблице:
, проходящей через центр масс тела, приведены в следующей таблице:
| Твердое тело | Ось 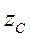
| Момент инерции |
тонкий стержень длины 
| перпендикулярна стержню | 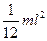
|
сплошной цилиндр радиуса 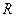
| совпадает с осью цилиндра | 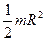
|
тонкий диск радиуса 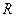
| совпадает с диаметром диска | 
|
шар радиуса 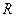
| проходит через центр шара | 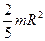
|
Вычисление момента инерции твердого тела произвольной формы относительно той или иной оси представляет собой, вообще говоря, довольно кропотливую в математическом отношении задачу. Однако в некоторых случаях нахождение момента инерции значительно упрощается, если воспользоваться теоремой Гюйгенса-Штейнера:момент инерции 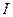 относительно произвольной оси
относительно произвольной оси 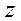 равен моменту инерции
равен моменту инерции 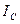 относительно оси
относительно оси 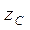 , параллельной данной и проходящей через центр масс
, параллельной данной и проходящей через центр масс 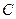 тела, плюс произведение массы
тела, плюс произведение массы  тела на квадрат расстояния
тела на квадрат расстояния  между осями:
между осями:
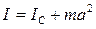 (4.13)
(4.13)
Основное уравнение динамики вращательного движения можно записать по аналогии с уравнением поступательного движения:
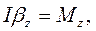 (4.14)
(4.14)
где 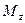 - суммарный момент всех внешних сил относительно оси вращения. Из этого уравнения видно, что момент инерции
- суммарный момент всех внешних сил относительно оси вращения. Из этого уравнения видно, что момент инерции 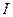 определяет инерционные свойства твердого тела при вращении: при одном и том же значении момента сил
определяет инерционные свойства твердого тела при вращении: при одном и том же значении момента сил 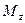 тело с большим моментом инерции приобретает меньшее угловое ускорение
тело с большим моментом инерции приобретает меньшее угловое ускорение  .
.
Интегрирование уравнения (4.14) с учетом начальных условий – значений 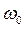 и
и 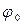 в начальный момент времени – позволяет полностью решить задачу о вращении твердого тела вокруг неподвижной оси, т.е. найти зависимость от времени угловой скорости и угла поворота,
в начальный момент времени – позволяет полностью решить задачу о вращении твердого тела вокруг неподвижной оси, т.е. найти зависимость от времени угловой скорости и угла поворота, 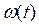 и
и 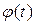 .
.
Заметим, что уравнение (4.14) справедливо в любой системе отсчета, жестко связанной с осью вращения. Однако если система отсчета неинерциальная, то момент сил 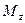 включает в себя не только моменты сил взаимодействия с другими телами, но и моменты сил инерции.
включает в себя не только моменты сил взаимодействия с другими телами, но и моменты сил инерции.
Экспериментальная часть
Для экспериментального доказательства соотношения (4.14) в работе используется маятник Обербека (рисунок 4.5). Он состоит из четырех стержней A и двух шкивов различного радиуса R1 и R2, укрепленных на одной горизонтальной оси. По стержням могут перемещаться и закрепляться в нужном положении четыре (по одному на каждом стержне) груза одинаковой массы m. При помощи груза массы m, прикрепленного к концу намотанной на тот или иной шкив нити, маятник может приводиться во вращение.
Пренебрегая силами трения и считая нить невесомой и нерастяжимой, можем написать:
уравнение вращательного движения маятника
 , (4.15)
, (4.15)
уравнение поступательного движения груза на нити
 , (4.16)
, (4.16)
уравнение кинематической связи
 , (4.17)
, (4.17)
где R — радиус шкива,
T — натяжение нити,
a — линейное ускорение груза массы m,
g — ускорение свободного падения.
Из системы уравнений (4.15 – 4.17) следует, что груз m должен двигаться с постоянным ускорением
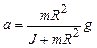 . (4.18)
. (4.18)
 Основное уравнение вращательного движения (4.14) было записано без учета момента сил трения в оси маятника и момента сил вязкого трения о воздух. Для доказательства правомерности такого подхода в процессе выполнения работы необходимо убедиться, что суммарный момент сил трения
Основное уравнение вращательного движения (4.14) было записано без учета момента сил трения в оси маятника и момента сил вязкого трения о воздух. Для доказательства правомерности такого подхода в процессе выполнения работы необходимо убедиться, что суммарный момент сил трения  много меньше момента силы натяжения нити
много меньше момента силы натяжения нити 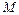 , который равен:
, который равен:
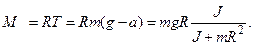
С учетом неравенства  << J можно записать, что
<< J можно записать, что 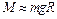 .
.
Оценить величину момента сил трения можно, если предположить, что он остается неизменным во время движения. При опускании груза m c отметки 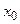 на полную длину нити до отметки
на полную длину нити до отметки  и при последующем подъеме до отметки
и при последующем подъеме до отметки 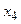 изменение его потенциальной энергии будет равно работе силы трения, т. е.
изменение его потенциальной энергии будет равно работе силы трения, т. е.
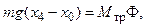
где Ф — полный угол поворота маятника Обербека. При этом
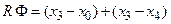 ,
,
поэтому
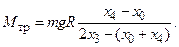
Таким образом, условие малости момента сил трения окончательно имеет вид
 . (4.19)
. (4.19)
Описание экспериментальной установки

Установка для изучения вращательного движения состоит из основания (1), вертикальной колонны (2) с закрепленными на ней двумя подвижными кронштейнами (3, 4), на которых крепятся оптические датчики положения. На колонне закреплены два неподвижных кронштейна (5, 6).
На нижнем кронштейне (5) закреплен двухступенчатый вал (7). На верхнем кронштейне (6) закреплен подшипниковый узел (8) и блок (9). Через блок перекинута нить (10), один конец которой намотан на двухступенчатый вал (7), а на втором конце закреплен груз (11). На двухступенчатом валу крепится тело маятника (12).
Кронштейны с фотодатчиками могут крепиться на разной высоте. Расстояние между этими кронштейнами измеряется по шкале, нанесенной на колонне. Время движения грузов определяют с помощью электронного таймера. Подготовка таймера к измерению осуществляется нажатием кнопки «Пуск», после перекрытия луча в первом фотодатчике таймер начинает измерение времени, после перекрытия луча во втором фотодатчике останавливается. При подготовке к дальнейшим измерениям результаты предыдущих измерений убираются с табло таймера нажатием кнопки «Сброс».
Проведение эксперимента
Упражнение 1. Проверка закона движения
Из (4.15)–(4.17) следует, что вращение маятника Обербека происходит с постоянным угловым ускорением , при этом груз m опускается с постоянным линейным ускорением a. Координата x груза, отпущенного без начальной скорости с отметки  , меняется по закону (ось х системы координат направлена вниз (см. рисунок 4.5)):
, меняется по закону (ось х системы координат направлена вниз (см. рисунок 4.5)):
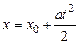 . (4.20)
. (4.20)
Используя (4.20), определим время t пролета груза между двумя отметками х1и х2:
 . (4.21)
. (4.21)
Из (4.21) следует, что в случае равнопеременного движения (a = сonst) и фиксированных положений  и
и  , зависимость времени t от
, зависимость времени t от 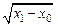 является линейной и изображается на графике прямой линией.
является линейной и изображается на графике прямой линией.
Измерения
1 Установить максимальное расстояние между кронштейнами с фотодатчиками.
2 Установить грузы m в среднее положение, разместив их на равном расстоянии от оси таким образом, чтобы маятник находился в положении безразличного равновесия. Начало движения груза m всегда осуществляют от одного и того же положения  , которое необходимо записать в рабочий журнал. Нить наматывают на вал большего диаметра виток к витку.
, которое необходимо записать в рабочий журнал. Нить наматывают на вал большего диаметра виток к витку.
3 Отпустить груз m и произвести измерение времени t пролета груза между фотодатчиками. Данные записать в таблицу 4.1. Провести измерения времени t для нескольких положений х1 верхнего датчика (рекомендуется менять х1 с шагом 5 см). Для каждого положения датчика измерения времени проводят не менее 3-х раз.
4 Для 5–7 первых опытов измерить значения  — отметки, до которой поднимается груз при вращении маятника в одну сторону. Результаты занести в таблицу 4.1.
— отметки, до которой поднимается груз при вращении маятника в одну сторону. Результаты занести в таблицу 4.1.
5 Определить значение  — максимальной отметки, до которой опускается груз m при своем движении.
— максимальной отметки, до которой опускается груз m при своем движении.
Таблица 4.1
| N | x1i | x4 | 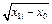
| 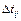
| 
| 
| 
| 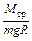
| |||
Обработка результатов
1 По экспериментальным данным для каждого положения фотодатчика 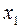 рассчитать среднее значение величины tiпо формуле
рассчитать среднее значение величины tiпо формуле
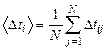 ,
,
где N — число измерений при каждом фиксированном положении датчика x1.
2 Вычислить погрешность измерения (выборочное стандартное отклонение) 
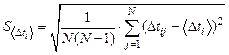 .
.
Результаты вычислений внести в таблицу 4.1.
3 Построить зависимость 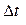 от
от 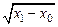 , которая должна быть линейной. Близость получившейся зависимости к линейной указывает на то, что движение тела является равнопеременным.
, которая должна быть линейной. Близость получившейся зависимости к линейной указывает на то, что движение тела является равнопеременным.
4 Найти среднее значение  и оценить величину
и оценить величину 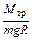 по формуле (4.19). Убедиться в малости момента сил трения по сравнению с начальным моментом силы натяжения нити.
по формуле (4.19). Убедиться в малости момента сил трения по сравнению с начальным моментом силы натяжения нити.
Упражнение 2. Проверка независимости инерционных свойств маятника (момента инерции) от момента внешних сил
В данном упражнении экспериментально показывается, что инерционные свойства маятника, а именно — момент инерции — не зависят от момента внешних сил.
Из уравнения (4.15) имеем
 (4.22)
(4.22)
Из уравнений (4.18), (4.21) следует, что
 (4.23)
(4.23)
В уравнение (4.23) входят величины, определяемые экспериментально.
Измерения
2 Установить максимальное расстояние между кронштейнами с фотодатчиками. Занести в рабочий журнал координаты фотодатчиков x1, x2 и значение х0. 3 Установить грузы в среднее положение, разместив их на равном расстоянии от… 4 На конец нити, намотанной на шкив радиуса R1, прикрепить груз массы m1и измерить время прохождения груза между двумя…Таблица 4.2
| Комбинации значений радиусов шки-вов и масс при измерениях | N | 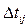
| x4 |  , ,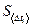
|  , ,

| 
| 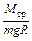
| ||||||

| |||||||||||||
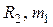
| |||||||||||||

| |||||||||||||

| |||||||||||||
Обработка результатов
1 По экспериментальным данным вычислить средние значения величин t и ошибки их измерений для четырех различных опытов. Результаты вычислений занести в таблицу 4.2.
2 Вычислить значения моментов инерции J1+J4по формуле (4.23).
3 Определить значение  для каждого опыта.
для каждого опыта.
4 Найти отношение 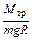 аналогично тому, как это было сделано в упр. 1. Результаты занести в таблицу 4.2.
аналогично тому, как это было сделано в упр. 1. Результаты занести в таблицу 4.2.
5 Произвести оценку погрешностей полученных результатов. Так как экспериментальные значения Jiявляются результатом косвенных измерений, то стандартное отклонение функции нескольких независимых переменных находится через погрешности прямых измерений по методу, описанному в 1-й части.
 6. Проанализировать полученный результат. Для этого отметить значения моментов инерции J1
6. Проанализировать полученный результат. Для этого отметить значения моментов инерции J1 J4.с учетом погрешностей на числовых осях (рисунок 4.6). Пересечение этих областей будет указывать на выполнение соотношения (4.22), что свидетельствует о независимости инерционных свойств маятника от момента внешних сил.
J4.с учетом погрешностей на числовых осях (рисунок 4.6). Пересечение этих областей будет указывать на выполнение соотношения (4.22), что свидетельствует о независимости инерционных свойств маятника от момента внешних сил.
Рисунок 4.6 - Сравнение моментов инерции
между собой для четырех опытов
Упражнение 3. Проверка основного уравнения вращательного движения и теоремы Гюйгенса–Штейнера
Пусть 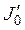 — суммарный момент инерции четырех грузов с массами m относительно осей, проходящих через их центры масс. При удалении центров грузов на расстояние
— суммарный момент инерции четырех грузов с массами m относительно осей, проходящих через их центры масс. При удалении центров грузов на расстояние  , от оси вращения (см. рисунок 4.5), согласно теореме Гюйгенса–Штейнера, момент инерции
, от оси вращения (см. рисунок 4.5), согласно теореме Гюйгенса–Штейнера, момент инерции  будет равен
будет равен
 (4.24)
(4.24)
Если J0 — момент инерции маятника без грузов, то полный момент инерции маятника будет равен
 (4.25)
(4.25)
При удалении центров масс грузов на расстояние  соответственно имеем
соответственно имеем
 (4.26)
(4.26)
С учетом уравнений (4.15)–(4.17) и (4.23) зависимость квадрата времени пролета груза между двумя отметками  и
и  от расстояния центра грузов
от расстояния центра грузов 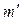 от оси вращения
от оси вращения 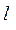 имеет вид
имеет вид
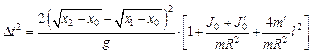 (4.27)
(4.27)
Если 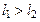 , то
, то
 (4.28)
(4.28)
Уравнения (4.27) и (4.28) дают
 (4.29)
(4.29)
где t1, t2 — времена пролета груза между датчиками для случаев l = l1, l = l2 соответственно.
В это уравнение входят величины, определяемые экспериментально.
Измерения
1 На конец нити, намотанной на шкив радиуса R2 (большего по размеру), прикрепить груз наибольшей массы. Фотодатчики оставить в том же положении, что и в упражнении 2.
2 Установить минимальное значение момента инерции маятника. Для этого грузы 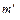 установить в положение, наиболее близкое к оси. Измерить расстояние от грузов до оси. Занести это значение в таблицу 4.3.
установить в положение, наиболее близкое к оси. Измерить расстояние от грузов до оси. Занести это значение в таблицу 4.3.
Таблица 4.3
| N | 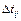
| x4 | 
| 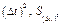
| 
| 
| 
| 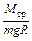
|
| ……….. |
3 Определить величину t — время прохождения груза 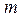 между двумя фотодатчиками и
между двумя фотодатчиками и 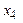 — отметку, до которой он поднимается в процессе движения. Измерения проводят 3 раза. Результаты заносят в таблицу 4.3.
— отметку, до которой он поднимается в процессе движения. Измерения проводят 3 раза. Результаты заносят в таблицу 4.3.
4 Изменяя положение грузов 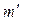 на стержнях с шагом 3 см, каждый раз измеряют время
на стержнях с шагом 3 см, каждый раз измеряют время 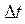 . Результаты измерения и соответствующие им расстояния l от оси маятника до центров грузов записать в таблицу 4.3. Одновременно для каждого опыта измеряют и заносят в таблицу 4.3 значения величины m.
. Результаты измерения и соответствующие им расстояния l от оси маятника до центров грузов записать в таблицу 4.3. Одновременно для каждого опыта измеряют и заносят в таблицу 4.3 значения величины m.
Обработка результатов
2 Вычислить погрешности измерения . 3 Построить график зависимости квадрата времени опускания груза (t)2от — это… 4 Проверить соотношение (4.29) для нескольких пар значений .Контрольные вопросы
1 Векторное произведение двух векторов: обозначение, модуль и направление. В чем заключается геометрический смысл векторного произведения двух векторов?
2 Какое тело называют твердым? Какое движение твердого тела называют поступательным и вращательным?
3 Покажите, что плоское движение твердого тела есть совокупность поступательного и вращательного движений твердого тела.
4 В чем заключается физический смысл выражений: 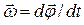 и
и 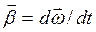 ? Покажите на рисунке взаимное расположение векторов
? Покажите на рисунке взаимное расположение векторов  ,
,  и
и 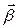 в случае ускоренного движения и замедленного движения.
в случае ускоренного движения и замедленного движения.
5 Сформулируйте задачу (прямую и обратную) кинематики вращательного движения.
6 Получите связь угловых кинематических величин с линейными величинами.
7 Момент инерции: определение, свойства. Момент инерции твердого тела.
8 Сформулируйте теорему Гюйгенса-Штейнера.
9 Момент силы относительно некоторой точки пространства и относительно некоторой неподвижной оси вращения 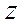 .
.
10 Сформулируйте основной закон вращательного движения и проведите аналогию с основным законом поступательного движения.
Рекомендуемая литература
4.4.1 Зисман, Г.А. Курс общей физики: в 3 т. / Г.А. Зисман, О.М. Тодес. – СПб.: Лань, 2007. – Т.1: Механика. Молекулярная физика. Колебания и волны. – 340 с. - ISBN 978-5-8114-0753-8.
4.4.2 Иродов, И.Е. Механика. Основные законы механики / И.Е.Иродов. - М.: Бином, 2009. – 310 с. - ISBN 978-5-9963-0063-1.
4.4.3 Савельев, И.В. Курс общей физики: в 5 кн. / И.В.Савельев. – М.: АСТРЕЛЬ: АСТ, 2005. – Кн. 1: Механика. – 336 с. - ISBN 5-271-01034-1.
4.4.4 Сивухин, Д.В. Общий курс физики: в 3 т. / Д.В.Сивухин. - М.: Физматлит, 2002. – Т. 1: Механика. – 560 с. - ISBN 5-89155-078-4.
Лабораторная работа №5. Теорема Гюйгенса-Штейнера
Цель работы: 1) изучение динамики вращательного движения.
2) изучение колебаний бифилярного и трифилярного подвеса.
3) экспериментальная проверка теоремы Гюйгенса–Штейнера и определение моментов инерции тел простой формы.
Теоретическая часть
 В экспериментальной части данной лабораторной работы используется связь между периодом колебаний крутильного маятника и его моментом инерции. В качестве маятника выбрана круглая платформа, подвешенная в поле тяжести на трех длинных нитях (трифилярный подвес). Платформа может совершать крутильные колебания вокруг вертикальной оси. На платформу помещаются тела различной формы, измеряются периоды колебаний маятника и определяются значения моментов инерции этих тел. Теорема Гюйгенса–Штейнера проверяется по соответствию между экспериментальной и теоретической зависимостями моментов инерции грузов от их расстояния до центра платформы.
В экспериментальной части данной лабораторной работы используется связь между периодом колебаний крутильного маятника и его моментом инерции. В качестве маятника выбрана круглая платформа, подвешенная в поле тяжести на трех длинных нитях (трифилярный подвес). Платформа может совершать крутильные колебания вокруг вертикальной оси. На платформу помещаются тела различной формы, измеряются периоды колебаний маятника и определяются значения моментов инерции этих тел. Теорема Гюйгенса–Штейнера проверяется по соответствию между экспериментальной и теоретической зависимостями моментов инерции грузов от их расстояния до центра платформы.
Кинетическая энергия вращающегося твердого тела
Рассмотрим вращение тела вокруг неподвижной оси  (рисунок 5.2). Линейная скорость элементарной массы
(рисунок 5.2). Линейная скорость элементарной массы  равна
равна
 ,
,
где  - расстояние массы
- расстояние массы  от оси
от оси  . Следовательно, для кинетической энергии
. Следовательно, для кинетической энергии 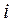 -й элементарной массы получается выражение
-й элементарной массы получается выражение


Кинетическая энергия тела слагается из кинетических энергий его частей:
 (5.1)
(5.1)
Рисунок 5.2
Пусть на массу  действуют внутренняя сила
действуют внутренняя сила 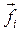 и внешняя сила
и внешняя сила 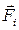 (рисунок 5.2). Эти силы совершают за время
(рисунок 5.2). Эти силы совершают за время  работу
работу

Осуществив в смешанных произведениях векторов циклическую перестановку сомножителей, получим

где 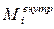 - момент внутренней силы относительно точки
- момент внутренней силы относительно точки 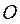 ,
,
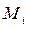 - аналогичный момент внешней силы.
- аналогичный момент внешней силы.
Просуммировав последнее выражение по всем элементарным массам, получим элементарную работу, совершаемую над телом за время  :
:

Сумма моментов внутренних сил равна нулю. Следовательно, обозначив суммарный момент внешних сил через 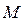 , придем к выражению
, придем к выражению
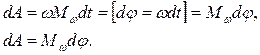 (5.2)
(5.2)
Итак, при вращении тела внутренние силы работы не совершают, работа же внешних сил определяется формулой (5.2). К формуле (5.2) можно прийти , воспользовавшись тем, что работа, совершаемая всеми приложенными к телу силами, идет на приращение его кинетической энергии. Взяв дифференциал от обеих частей равенства (5.1), придем к соотношению

Таблица 5.1
| Поступательное движение | Вращательное движение |
 - линейная скорость - линейная скорость
| 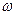 - угловая скорость - угловая скорость
|
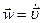 - линейное ускорение - линейное ускорение
|  - угловое ускорение - угловое ускорение
|
 - масса - масса
|  - момент инерции - момент инерции
|
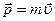 - импульс - импульс
| 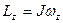 - момент импульса* - момент импульса*
|
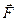 - сила - сила
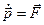
| 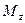 - момент силы - момент силы

|

| 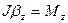 * *
|
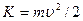
| 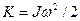 * *
|
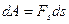
| 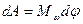
|
| * Для неподвижной оси вращения |
В таблице 5.1 сопоставлены формулы механики вращательного движения с аналогичными формулами механики поступательного движения (механики точки). Из этого сопоставления видно, что во всех случаях роль массы играет момент инерции, роль силы – момент силы, роль импульса – момент импульса и т.д.
Бифилярный и трифилярный подвесы
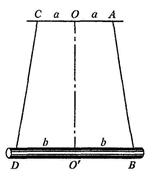 1 Найдем период малых колебаний бифилярного подвеса. Так называется устройство, состоящее из двух нитей
1 Найдем период малых колебаний бифилярного подвеса. Так называется устройство, состоящее из двух нитей 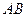 и
и  (рисунок 5.3) одинаковой длины, на которых подвешено некоторое тело
(рисунок 5.3) одинаковой длины, на которых подвешено некоторое тело  . Если тело повернуть вокруг вертикальной оси
. Если тело повернуть вокруг вертикальной оси 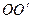 , то оно начнет совершать крутильные колебания вокруг этой оси. Бифилярный подвес есть система с одной степенью свободы. В качестве координаты, определяющей ее мгновенное положение, удобно взять угол поворота
, то оно начнет совершать крутильные колебания вокруг этой оси. Бифилярный подвес есть система с одной степенью свободы. В качестве координаты, определяющей ее мгновенное положение, удобно взять угол поворота 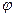 тела
тела  вокруг оси
вокруг оси 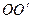 , отсчитывая этот угол от положения равновесия.
, отсчитывая этот угол от положения равновесия.
Рисунок 5.3
Кинетическая энергия системы равна
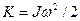 ,
,
где  - момент инерции ее относительно оси
- момент инерции ее относительно оси 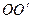 . Потенциальная энергия равна
. Потенциальная энергия равна
 ,
,
где 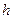 - высота поднятия тела
- высота поднятия тела  , отсчитываемая от его нижнего положения.
, отсчитываемая от его нижнего положения.
Пусть  означает длину
означает длину 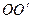 в положении равновесия,
в положении равновесия,  - расстояние между точками подвеса
- расстояние между точками подвеса 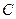 и
и  ,
,  - расстояние
- расстояние  . Предполагается, что система симметрична, так что точки
. Предполагается, что система симметрична, так что точки  и
и 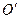 являются серединами отрезков
являются серединами отрезков 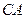 и
и  . Высота
. Высота 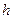 найдется из условия нерастяжимости нитей
найдется из условия нерастяжимости нитей 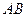 и
и 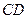 . Введем прямоугольную систему координат с началом в точке
. Введем прямоугольную систему координат с началом в точке  , ось
, ось 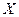 направим вдоль прямой
направим вдоль прямой  , ось
, ось  - вниз вдоль прямой
- вниз вдоль прямой 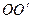 , ось
, ось  - перпендикулярно к ним. Координаты точки
- перпендикулярно к ним. Координаты точки  все время остаются постоянными и равны
все время остаются постоянными и равны
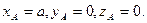
Координаты точки  в положении равновесия равны
в положении равновесия равны
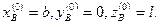
При повороте системы на угол 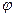 координаты той же точки становятся равными
координаты той же точки становятся равными

Условие постоянства длины нити 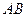 можно записать в виде
можно записать в виде

или 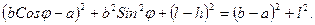
После простых преобразований отсюда находим

При малых колебаниях можно положить  Кроме того,
Кроме того, 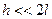 , и величиной
, и величиной 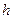 в знаменателе можно пренебречь. В этом приближении
в знаменателе можно пренебречь. В этом приближении
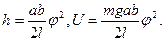
Потенциальная и кинетическая энергии приводятся к виду 
где 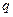 - обобщенная координата,
- обобщенная координата,
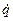 - обобщенная скорость.
- обобщенная скорость.
Известно, что если уравнение энергии приводится к такому виду, то движение механической системы с одной степенью свободы есть гармонические колебания:
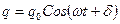 ,
,
причем частота колебания  .
.
В нашем случае колебания системы будут гармоническими с периодом
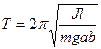 .
.
Период колебаний пропорционален корню квадратному из момента инерции и обратно пропорционален корню квадратному из массы системы. Возьмем в качестве тела  металлический стержень. Выведем его из положения равновесия и заставим совершать крутильные колебания. Они будут сравнительно медленными. Прикрепим затем в точке
металлический стержень. Выведем его из положения равновесия и заставим совершать крутильные колебания. Они будут сравнительно медленными. Прикрепим затем в точке 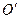 тяжелый груз и снова заставим систему колебаться. Колебания станут значительно более быстрыми. Дело в том, что груз прикреплен на оси вращения, а потому он, значительно увеличивая массу системы, практически не влияет на ее момент инерции. Уменьшение периода колебаний можно объяснить также следующим образом. В положение равновесия система возвращается под действием горизонтальных составляющих сил натяжения нитей. Подвешивая груз, мы сильно увеличиваем натяжение нитей, а момент инерции увеличивается незначительно. Это и приводит к тому, что колебания становятся более быстрыми.
тяжелый груз и снова заставим систему колебаться. Колебания станут значительно более быстрыми. Дело в том, что груз прикреплен на оси вращения, а потому он, значительно увеличивая массу системы, практически не влияет на ее момент инерции. Уменьшение периода колебаний можно объяснить также следующим образом. В положение равновесия система возвращается под действием горизонтальных составляющих сил натяжения нитей. Подвешивая груз, мы сильно увеличиваем натяжение нитей, а момент инерции увеличивается незначительно. Это и приводит к тому, что колебания становятся более быстрыми.
2 Трифилярный подвес представляет собой круглую платформу радиуса 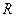 , подвешенную на трех симметрично расположенных нитях одинаковой длины, укрепленных у ее краев (рисунок 5.1). Наверху эти нити также симметрично прикреплены к диску несколько меньшего размера (радиуса
, подвешенную на трех симметрично расположенных нитях одинаковой длины, укрепленных у ее краев (рисунок 5.1). Наверху эти нити также симметрично прикреплены к диску несколько меньшего размера (радиуса  ). Платформа может совершать крутильные колебания вокруг вертикальной оси
). Платформа может совершать крутильные колебания вокруг вертикальной оси 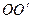 , перпендикулярной к ее плоскости и проходящей через ее центр. Такое движение платформы приводит к изменению положения ее центра тяжести по высоте.
, перпендикулярной к ее плоскости и проходящей через ее центр. Такое движение платформы приводит к изменению положения ее центра тяжести по высоте.
Если платформа массы  , вращаясь в одном направлении, поднялась на высоту
, вращаясь в одном направлении, поднялась на высоту 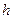 , то приращение потенциальной энергии будет равно
, то приращение потенциальной энергии будет равно
 (5.3)
(5.3)
Вращаясь в другом направлении, платформа придет в положение равновесия (h = 0) с кинетической энергией, равной
 (5.4)
(5.4)
где  — момент инерции платформы,
— момент инерции платформы,
 — угловая скорость вращения платформы в момент прохождения ею положения равновесия.
— угловая скорость вращения платформы в момент прохождения ею положения равновесия.
Пренебрегая работой сил трения, на основании закона сохранения механической энергии имеем
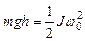 . (5.5)
. (5.5)
Считая, что платформа совершает гармонические крутильные колебания, можно записать зависимость углового смещения платформы 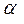 от времени t в виде
от времени t в виде
 , (5.6)
, (5.6)
где 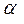 — угловое смещение платформы,
— угловое смещение платформы,
 — угол максимального поворота платформы, т.е. амплитуда углового смещения,
— угол максимального поворота платформы, т.е. амплитуда углового смещения,
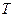 — период колебаний.
— период колебаний.
Для угловой скорости  , являющейся первой производной по времени от величины углового смещения, можно записать
, являющейся первой производной по времени от величины углового смещения, можно записать
 . (5.7)
. (5.7)
В моменты прохождения платформы через положение равновесия величина 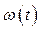 будет максимальна и равна по модулю
будет максимальна и равна по модулю
 . (5.8)
. (5.8)
Из выражений (5.5) и (5.8) следует, что
 . (5.9)
. (5.9)
Если  — длина нитей подвеса,
— длина нитей подвеса, 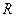 — расстояние от центра платформы до точек крепления нитей на ней,
— расстояние от центра платформы до точек крепления нитей на ней,  — радиус верхнего диска (рисунок 5.1), то легко видеть, что
— радиус верхнего диска (рисунок 5.1), то легко видеть, что
 . (5.10)
. (5.10)
Так как
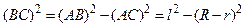 , (5.11)
, (5.11)
а при максимальном отклонении платформы от положения равновесия
 , (5.12)
, (5.12)
то
 . (5.13)
. (5.13)
При малых углах отклонения 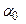 значение синуса этого угла можно заменить просто значением
значение синуса этого угла можно заменить просто значением 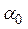 . Учитывая также, что при
. Учитывая также, что при 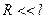 величину знаменателя можно положить равной
величину знаменателя можно положить равной 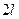 , получаем
, получаем
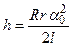 . (5.14)
. (5.14)
При этом закон сохранения энергии (9) примет вид:
 . (5.15)
. (5.15)
откуда следует, что
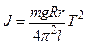 . (5.16)
. (5.16)
По формуле (5.16) можно экспериментально определить момент инерции пустой платформы или платформы с телом, положенным на нее, так как все величины в правой части формулы непосредственно измеряются. Следует помнить, что  — это суммарная масса платформы и исследуемого тела, положенного на нее.
— это суммарная масса платформы и исследуемого тела, положенного на нее.
 Соотношение (5.16) используется в лабораторной работе для определения моментов инерции тел простой формы и подтверждения справедливости теоремы Гюйгенса–Штейнера.
Соотношение (5.16) используется в лабораторной работе для определения моментов инерции тел простой формы и подтверждения справедливости теоремы Гюйгенса–Штейнера.
Моменты инерции прямоугольной пластины относительно главных центральных осей. Для расчета моментов инерции прямоугольной пластинки со сторонами 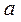 и
и  и массой
и массой 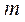 выберем систему координат так, чтобы ее оси совпадали с главными центральными осями (рисунок 5.4). Для прямоугольной пластинки легко вычислить моменты инерции относительно осей
выберем систему координат так, чтобы ее оси совпадали с главными центральными осями (рисунок 5.4). Для прямоугольной пластинки легко вычислить моменты инерции относительно осей  и
и  . Рассмотрим, например, расчет
. Рассмотрим, например, расчет  . Пластинку можно представить как совокупность тонких полосок, для каждой из которых момент инерции вычисляется так же, как для тонкой палочки длины
. Пластинку можно представить как совокупность тонких полосок, для каждой из которых момент инерции вычисляется так же, как для тонкой палочки длины 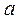 . Момент инерции пластинки относительно оси
. Момент инерции пластинки относительно оси  равен сумме моментов инерции этих полосок, т.е.
равен сумме моментов инерции этих полосок, т.е.
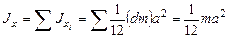 . (5.17)
. (5.17)
Аналогично вычисляется момент инерции пластинки относительно оси 
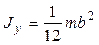 (5.18)
(5.18)
Для вычисления момента инерции пластинки относительно оси z воспользуемся следующим приемом. Рассмотрим малый элемент массы  (рисунок 5.5). Его момент инерции
(рисунок 5.5). Его момент инерции  относительно оси
относительно оси  равен
равен
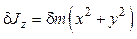 , (5.19)
, (5.19)
т.е. можно записать, что
 , (5.20)
, (5.20)
где 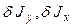 — моменты инерции этого малого элемента относительно осей
— моменты инерции этого малого элемента относительно осей  и
и  .
.
Это же соотношение справедливо не только для отдельного элемента, но и для любого плоского тела в целом. В этом легко убедиться, представляя плоское тело как совокупность отдельных малых элементов (рисунок 5.5) и производя суммирование по всем этим элементам.
Таким образом, используя (5.17), (5.18) и (5.20), получим
 . (5.21)
. (5.21)
 Момент инерции треугольной пластины относительно главной центральной оси, перпендикулярной его плоскости. Определим момент инерции треугольной пластины с помощью метода подобия. Этот метод используется обычно в тех случаях, когда изначально ясен общий вид формулы, определяющей момент инерции. В частности, если тело является правильной фигурой, например, квадратом, равносторонним треугольником, то в конечное выражение для момента инерции относительно оси, проходящей через центр масс и перпендикулярной плоскости фигуры, войдет масса тела и квадрат его характерного размера. Действительно — это единственные параметры, которые могут характеризовать инерционные свойства тела при его вращении вокруг выбранной оси. Таким образом, можно записать
Момент инерции треугольной пластины относительно главной центральной оси, перпендикулярной его плоскости. Определим момент инерции треугольной пластины с помощью метода подобия. Этот метод используется обычно в тех случаях, когда изначально ясен общий вид формулы, определяющей момент инерции. В частности, если тело является правильной фигурой, например, квадратом, равносторонним треугольником, то в конечное выражение для момента инерции относительно оси, проходящей через центр масс и перпендикулярной плоскости фигуры, войдет масса тела и квадрат его характерного размера. Действительно — это единственные параметры, которые могут характеризовать инерционные свойства тела при его вращении вокруг выбранной оси. Таким образом, можно записать
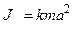 , (5.22)
, (5.22)
где  — момент инерции тела,
— момент инерции тела,
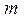 — его масса,
— его масса,
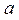 — характерный размер (сторона квадрата или треугольника),
— характерный размер (сторона квадрата или треугольника),
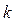 — неизвестный коэффициент, который определяется формой тела.
— неизвестный коэффициент, который определяется формой тела.
Для пластины, имеющей вид правильного треугольника 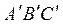 (рисунок 5.6), момент инерции относительно оси, перпендикулярной плоскости пластины и проходящей через точку
(рисунок 5.6), момент инерции относительно оси, перпендикулярной плоскости пластины и проходящей через точку 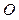 , может быть выражен формулой (5.22).
, может быть выражен формулой (5.22).
Проведем геометрическое построение (рисунок 5.6) и рассмотрим треугольную пластину  со стороной
со стороной  . Очевидно, что ее масса будет равна
. Очевидно, что ее масса будет равна 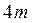 , а формула для момента инерции будет иметь вид
, а формула для момента инерции будет иметь вид
 . (23)
. (23)
Пластина  состоит из четырех одинаковых треугольников со стороной
состоит из четырех одинаковых треугольников со стороной 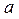 каждая. В этом случае момент инерции треугольника
каждая. В этом случае момент инерции треугольника  можно представить в виде суммы моментов инерции четырех треугольных пластин. Для вычисления этих моментов инерции воспользуемся тем, что центр масс треугольника находится в точке пересечения его медиан. Обозначим через
можно представить в виде суммы моментов инерции четырех треугольных пластин. Для вычисления этих моментов инерции воспользуемся тем, что центр масс треугольника находится в точке пересечения его медиан. Обозначим через  расстояние от центров
расстояние от центров 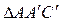 ,
,  ,
,  до точки
до точки 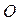 — центра масс пластины
— центра масс пластины  . Используя теорему Гюйгенса–Штейнера, получаем:
. Используя теорему Гюйгенса–Штейнера, получаем:

 (5.24)
(5.24)
Учитывая, что  , и сравнивая (5.24) с (5.18), находим, что
, и сравнивая (5.24) с (5.18), находим, что
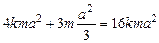 , (5.25)
, (5.25)
откуда следует
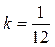 . (5.26)
. (5.26)
Таким образом, момент инерции плоского тела, имеющего форму равностороннего треугольника, относительно оси, проходящей через центр масс (точку О) перпендикулярно его плоскости, равен
 . (5.27)
. (5.27)
Моменты инерции тонкого диска относительно его главных центральных осей.
Для расчета моментов инерции тонкого диска массы 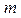 и радиуса
и радиуса 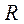 выберем систему координат так, чтобы ее оси совпадали с главными центральными осями (рисунок 5.7). Определим момент инерции тонкого однородного диска относительно оси
выберем систему координат так, чтобы ее оси совпадали с главными центральными осями (рисунок 5.7). Определим момент инерции тонкого однородного диска относительно оси  , перпендикулярной к плоскости диска. Рассмотрим бесконечно тонкое кольцо с внутренним радиусом
, перпендикулярной к плоскости диска. Рассмотрим бесконечно тонкое кольцо с внутренним радиусом 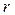 и наружным
и наружным 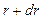 . Площадь такого кольца
. Площадь такого кольца  , а его масса
, а его масса 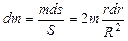 , где
, где  — площадь всего диска. Момент инерции тонкого кольца найдется по формуле
— площадь всего диска. Момент инерции тонкого кольца найдется по формуле  . Момент инерции всего диска определяется интегралом
. Момент инерции всего диска определяется интегралом
 . (5.28)
. (5.28)
Для определения 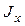 воспользуемся симметрией диска
воспользуемся симметрией диска 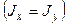 и утверждением (5.20), полученным при расчете момента инерции прямоугольной пластины. При этом из (5.20) получаем
и утверждением (5.20), полученным при расчете момента инерции прямоугольной пластины. При этом из (5.20) получаем
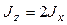 , (5.29)
, (5.29)
откуда
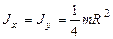 . (5.30)
. (5.30)
Экспериментальная часть
Экспериментальная установка
Тела на платформу необходимо класть строго симметрично, так, чтобы не было перекоса платформы. Для облегчения определения положения грузов и более… Вращательный импульс, необходимый для запуска крутильных колебаний, сообщается… Для измерения периода колебаний используется секундомер. Чтобы увеличить точность, следует измерять время 10-20…Проведение эксперимента
Упражнение 1. Проверка теоремы Гюйгенса–Штейнера
Измерения
1 Произвести взвешивание грузов. 2 Установить грузы в центре платформы, положив их один на другой. Создать…Таблица 5.2
| Номер опыта | a | a2 | n | tn | 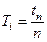
| Ji |
| …………. |
3 Расположить грузы симметрично на платформе. Провести измерения времени колебаний 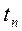 для 5–7 положений грузов, постепенно перемещая их к краям платформы. Рекомендуется проводить измерения через 1 см. Занести в таблицу 5.2 значения расстояний от центра масс каждого тела до центра платформы, число колебаний n и значения времени этих колебаний
для 5–7 положений грузов, постепенно перемещая их к краям платформы. Рекомендуется проводить измерения через 1 см. Занести в таблицу 5.2 значения расстояний от центра масс каждого тела до центра платформы, число колебаний n и значения времени этих колебаний 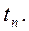
Обработка результатов
2 Занести в таблицу значения 3 Для каждого положения грузов найти значения момента инерции платформы с… 4 Полученные значения нанести на график зависимости момента инерции системы тел от квадрата расстояния центра масс…Измерения
2 Платформу поочередно нагружают исследуемыми телами таким образом, чтобы их центр масс совпадал с осью вращения платформы. Масса этих тел известна…Таблица 5.3
| Тело | № опыта | n | tn | <tn> | St | T | ST | J | SJ | |
| 1. Пустая платформа | ||||||||||
| 2. Платформа с квадратной пластиной | ||||||||||
| 3. Платформа с треугольной пластиной | ||||||||||
| ………….. |
Обработка результатов
. 2 Найти средние арифметические значения и среднеквадратичные отклонения для… 3 По формуле (5.16) определить величины ,,и среднеквадратичные отклонения этих величин.Основные итоги работы
В результате выполнения работы должна быть проведена проверка выполнения теоремы Гюйгенса–Штейнера. Должно быть также проведено сравнение экспериментально найденного значения момента инерции для тела заданной формы с соответствующим значением, рассчитанным теоретически.
Контрольные вопросы
1 Кинематика вращательного движения.
2 Кинетическая энергия тела при его вращении вокруг неподвижной оси.
3 Аналогия между физическими величинами поступательного движения и вращательного движения.
4 Гармоническое колебание: формула, превращения механической энергии при гармоническом колебании. Период, частота и циклическая частота гармонического колебания.
5 Бифилярный подвес и вывод формулы для периода колебаний данной системы.
6 Трифилярный подвес. Метод измерения момента инерции исследуемого тела с помощью крутильных колебаний.
7 Выведите момент инерции прямоугольной пластины относительно ее главных осей.
8 Выведите момент инерции треугольной пластины относительно главной центральной оси, перпендикулярной его плоскости.
9 Выведите момент инерции тонкого диска относительно его главных центральных осей.
Рекомендуемая литература
5.4.1 Зисман, Г.А. Курс общей физики: в 3 т. / Г.А. Зисман, О.М. Тодес. – СПб.: Лань, 2007. – Т.1: Механика. Молекулярная физика. Колебания и волны. – 340 с. - ISBN 978-5-8114-0753-8.
5.4.2 Иродов, И.Е. Механика. Основные законы механики / И.Е.Иродов. - М.: Бином, 2009. – 310 с. - ISBN 978-5-9963-0063-1.
5.4.3 Савельев, И.В. Курс общей физики: в 5 кн. / И.В.Савельев. – М.: АСТРЕЛЬ: АСТ, 2005. – Кн. 1: Механика. – 336 с. - ISBN 5-271-01034-1.
5.4.4 Сивухин, Д.В. Общий курс физики: в 3 т. / Д.В.Сивухин. - М.: Физматлит, 2002. – Т. 1: Механика. – 560 с. - ISBN 5-89155-078-4.
5.4.5 Трофимова, Т.И. Физика в таблицах и формулах / Т.И. Трофимова. – М.: Академия, 2006. – 448 с. - ISBN 5-7695-2277-1.
Лабораторная работа №6. Определение момента инерции колеса
Цель работы:1) изучение динамики вращательного движения твердого тела.
2) знакомство с методами определения момента инерции твердого тела.
3) определение момента инерции колеса.
Теоретическая часть
Уравнение вращательного движения для твердого тела, закрепленного на оси, имеет вид
 , (6.1)
, (6.1)
где J — момент инерции твердого тела относительно оси вращения,
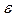 — его угловое ускорение,
— его угловое ускорение,
M — момент внешних сил, приложенных к телу.
Величина момента инерции относительно какой-либо оси определяется пространственным распределением массы тела. В частности, для тела, состоящего из конечного числа элементарных (малых) масс 
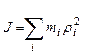 , (6.2)
, (6.2)
где  - расстояние от элементарной массы до оси вращения. В общем случае, для сплошных тел, суммирование заменяется интегрированием:
- расстояние от элементарной массы до оси вращения. В общем случае, для сплошных тел, суммирование заменяется интегрированием:
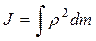 .
.
Для некоторых тел простой формы, возможен прямой расчет момента инерции. При сложной форме тела и неравномерном распределении его плотности аналитический расчет величины момента инерции может стать достаточно сложной задачей.
Вычисление моментов инерции во многих случаях можно упростить, используя соображения подобия и симметрии, теорему Гюйгенса-Штейнера, а также некоторые другие общие соотношения, о которых идет речь ниже.
Рассмотрим два подобных и подобно расположенных относительно оси вращения тела А и В одной и той же плотности. Полные и элементарные массы этих тел относятся как кубы их линейных размеров  . Так как элементарные массы умножаются на квадраты расстояний их до оси вращения, то моменты инерции тел А и В будут относиться как пятые степени тех же размеров. Таким образом,
. Так как элементарные массы умножаются на квадраты расстояний их до оси вращения, то моменты инерции тел А и В будут относиться как пятые степени тех же размеров. Таким образом,  , или
, или
 (6.3)
(6.3)
Под  следует понимать какой-либо характерный размер тела или расстояние какой-либо характерной точки его от оси вращения. Коэффициент пропорциональности
следует понимать какой-либо характерный размер тела или расстояние какой-либо характерной точки его от оси вращения. Коэффициент пропорциональности  зависит только от формы тела и его расположения относительно оси вращения.
зависит только от формы тела и его расположения относительно оси вращения.
Вычисление момента инерции тела относительно оси часто можно упростить, вычислив предварительно момент инерции его относительно точки. Рассмотрим сначала одну материальную точку с массой 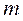 и с координатами
и с координатами 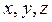 относительно прямоугольной системы координат (рисунок 6.1).
относительно прямоугольной системы координат (рисунок 6.1).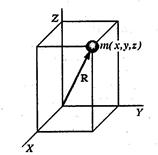
Рисунок 6.1
Квадраты расстояний ее до координатных осей  равны соответственно
равны соответственно  , а моменты инерции относительно тех же осей
, а моменты инерции относительно тех же осей

Сложив эти три равенства, получим
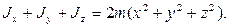
Но  , где
, где 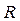 – расстояние точки
– расстояние точки 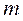 от начала координат
от начала координат  . Поэтому
. Поэтому
 . (6.4)
. (6.4)
Это соотношение справедливо не только для одной материальной точки, но и для произвольного тела, так как тело можно рассматривать как совокупность материальных точек. Таким образом, сумма моментов инерции тела относительно трех взаимно перпендикулярных осей, пересекающихся в одной точке  , равна удвоенному моменту инерции того же тела относительно этой точки.
, равна удвоенному моменту инерции того же тела относительно этой точки.
Если повернуть координатные оси  относительно тела, оставляя углы между ними прямыми, то моменты инерции
относительно тела, оставляя углы между ними прямыми, то моменты инерции  , вообще говоря, изменятся. Однако их сумма останется той же самой, так как она равна
, вообще говоря, изменятся. Однако их сумма останется той же самой, так как она равна 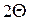 , а величина
, а величина  не зависит от ориентации координатных осей. Таким образом, сумма моментов инерции
не зависит от ориентации координатных осей. Таким образом, сумма моментов инерции  относительно любых трех взаимно перпендикулярных осей, проходящих через одну точку, зависит от положения этой же точки и не меняется с изменением ориентации осей.
относительно любых трех взаимно перпендикулярных осей, проходящих через одну точку, зависит от положения этой же точки и не меняется с изменением ориентации осей.
Момент инерции тонкого стержня, относительно оси, проходящей через его середину. Пусть тонкий стержень имеет длину l и массу m. Разделим его на малые элементы длины dx (рисунок 6.2), масса которых  . Если выбранный элемент находится на расстоянии x от оси, то его момент инерции
. Если выбранный элемент находится на расстоянии x от оси, то его момент инерции 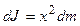 , т.е.
, т.е.

Интегрируя последнее соотношение в пределах от 0 до l/2 и удваивая полученное выражение (для учета левой половины стержня), получим

 . (6.5)
. (6.5)
Это выражение может быть получено и другим способом, с помощью метода подобия. Будем считать, что рассматриваемый стержень состоит из двух половин (рисунок 6.3). Каждая из них имеет массу m/2 и длину l/2. Выражение для момента инерции стержня должно включать его массу и длину, так как это единственные параметры, определяющие его инерционные свойства при вращении. Пусть
 , (6.6)
, (6.6)
где  — неизвестный коэффициент.
— неизвестный коэффициент.
Для каждой из половин стержня при вращении вокруг оси  можно найти момент инерции, используя (6.6) и теорему Гюйгенса–Штейнера:
можно найти момент инерции, используя (6.6) и теорему Гюйгенса–Штейнера:
 (6.7)
(6.7)
Полный момент инерции стержня
 (6.8)
(6.8)
Но этот же момент инерции, согласно (6.6), равен 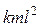 . Приравнивая (6.6) и (6.8), имеем
. Приравнивая (6.6) и (6.8), имеем
 (6.9)
(6.9)
или  и, следовательно,
и, следовательно,
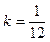 , (6.10)
, (6.10)
т.е. , что совпадает с (6.5).
, что совпадает с (6.5).
Моменты инерции цилиндра относительно его главных центральных осей. Выберем оси системы координат, совпадающие с главными центральными осями так, как показано на рисунке 6.4. Определим момент инерции цилиндра относительно оси 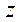 . Цилиндр представляет собой набор тонких дисков с массами
. Цилиндр представляет собой набор тонких дисков с массами  и моментами инерции
и моментами инерции  . Момент инерции цилиндра равен сумме моментов инерций
. Момент инерции цилиндра равен сумме моментов инерций 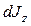 тонких дисков
тонких дисков
 , (6.11)
, (6.11)
где  — радиус цилиндра,
— радиус цилиндра,
 — его масса.
— его масса.
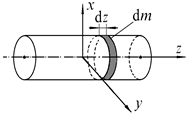
Рисунок 6.4 - Выбор системы координат и представление
цилиндра в виде набора тонких дисков

Пусть теперь ось вращения проходит через центр масс цилиндра перпендикулярно его продольной оси (рисунок 6.4) и совпадает с осью координат  . Представим цилиндр как совокупность тонких дисков толщины
. Представим цилиндр как совокупность тонких дисков толщины  и массы
и массы  (
( — длина цилиндра). Момент инерции тонкого диска
— длина цилиндра). Момент инерции тонкого диска  относительно оси
относительно оси  с помощью теоремы Гюйгенса–Штейнера равен
с помощью теоремы Гюйгенса–Штейнера равен
 , (6.12)
, (6.12)
где  — расстояние от диска до центра цилиндра.
— расстояние от диска до центра цилиндра.
Момент инерции всего цилиндра найдем после интегрирования по  (по всей длине цилиндра):
(по всей длине цилиндра):
 , (6.13)
, (6.13)
откуда получаем
 . (6.14)
. (6.14)
Момент инерции цилиндра с центральным отверстием относительно его продольной оси. Однородный цилиндр массы 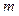 с внешним радиусом
с внешним радиусом 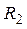 и внутренним радиусом
и внутренним радиусом 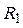 (рисунок 6.5) можно рассматривать как сплошной цилиндр радиуса
(рисунок 6.5) можно рассматривать как сплошной цилиндр радиуса  , массы
, массы 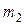 , из которого вырезано отверстие — цилиндр радиуса
, из которого вырезано отверстие — цилиндр радиуса 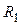 , массы
, массы  . Очевидно, что
. Очевидно, что 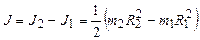 и, так как
и, так как 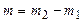 и
и  , то
, то
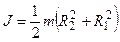 . (6.15)
. (6.15)
Момент инерции шара. Сплошной шар массы  и радиуса
и радиуса  можно рассматривать как совокупность бесконечно тонких сферических слоев с массами
можно рассматривать как совокупность бесконечно тонких сферических слоев с массами  , радиусом
, радиусом 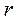 , толщиной
, толщиной 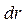 (рисунок 6.6).
(рисунок 6.6).
Рассмотрим малый элемент сферического слоя  с координатами x, y, x. Его моменты инерции относительно осей
с координатами x, y, x. Его моменты инерции относительно осей  проходящих через центр слоя —
проходящих через центр слоя — 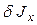 ,
,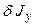 ,
,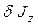 , равны
, равны
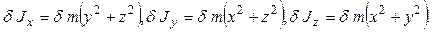
Таким образом, можно записать
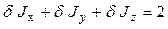
 (6.16)
(6.16)
Так как для элементов сферического слоя 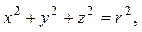 то
то
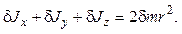
После интегрирования по всему объему слоя получим
 (6.17)
(6.17)
Так как, в силу симметрии для сферического слоя
 , а
, а 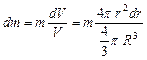
 ,
,
то
 .
.
Интегрируя по всему объему шара, получаем
 .
.
Окончательно (после интегрирования) получим, что момент инерции шара относительно оси, проходящей через его центр равен
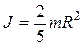 (6.18)
(6.18)
В данной работе применяются два способа экспериментального определения момента инерции: с помощью анализа колебаний физического маятника, составной частью которого является исследуемое тело, и с помощью изучения вращательного движения этого тела.
Определение момента инерции твердого тела на основе анализа его колебаний как физического маятника.
Уравнение движения такого маятника имеет вид , (6.19) где — моменты инерции твердого тела А и дополнительного грузика B относительно оси О,Экспериментальная часть
Экспериментальная установка
Проведение эксперимента
Упражнение 1. Определение момента инерции колеса методом колебаний
Измерения
2 После этого не менее трех раз измеряют расстояние L от оси вращения до центра масс груза. Результаты заносятся в таблицу 6.1.Таблица 6.1
| N | n | tn | Tn | <T> | ST | Ln | <L> | SL | mк, mг | J | SJ |
3 Взвешивают груз и съемный стакан для его крепления. Значение суммарной массы  заносят в таблицу 6.1.
заносят в таблицу 6.1.
Обработка результатов
2 Вычислить выборочные стандартные отклонения (средне-квадратичные ошибки среднего арифметического) для Т и L. 3 По полученным данным, пользуясь уравнением (6.25) и учитывая, что в этом… 4 Оценить погрешности для , используя следующую формулу для расчета погрешностей косвенных измерений:Измерения
2 Несколько раз измерить радиус цилиндра, на который наматывается нить.Таблица 6.2
| n | x1 | x2 | Dt | аn | <а> | Sa | x0 | x3 | x4 | 
| <Mтр> | SMтр | |
| ………….. | |||||||||||||
Обработка результатов
2 Поскольку , определяются для различных значений , то будем считать полученные значения ускорений и моментов сил трения независимыми. Найти… 3 Вычислить выборочное среднее значение радиуса цилиндра и среднеквадратичную… 4 По формуле (6.29) определить значение момента инерции колеса и его погрешность.Рекомендуемая литература
6.4.1 Зисман, Г.А. Курс общей физики: в 3 т. / Г.А. Зисман, О.М. Тодес. – СПб.: Лань, 2007. – Т.1: Механика. Молекулярная физика. Колебания и волны. – 340 с. - ISBN 978-5-8114-0753-8.
6.4.2 Иродов, И.Е. Механика. Основные законы механики / И.Е.Иродов. - М.: Бином, 2009. – 310 с. - ISBN 978-5-9963-0063-1.
6.4.3 Савельев, И.В. Курс общей физики: в 5 кн. / И.В.Савельев. – М.: АСТРЕЛЬ: АСТ, 2005. – Кн. 1: Механика. – 336 с. - ISBN 5-271-01034-1.
6.4.4 Сивухин, Д.В. Общий курс физики: в 3 т. / Д.В.Сивухин. - М.: Физматлит, 2002. – Т. 1: Механика. – 560 с. - ISBN 5-89155-078-4.
6.4.5 Трофимова, Т.И. Физика в таблицах и формулах / Т.И. Трофимова. – М.: Академия, 2006. – 448 с. - ISBN 5-7695-2277-1.
Лабораторная работа №7. Закон сохранения момента количества движения
Цель работы: 1) изучение динамики вращательного движения.
2) проверка закона сохранения момента количества движения (импульса).
Теоретическая часть
Анализ поведения систем показывает, что кроме энергии и импульса существует еще одна механическая величина, с которой также связан закон сохранения, - это момент импульса (момент количества движения).
 Момент импульса частицы. Рассмотрим частицу, пусть
Момент импульса частицы. Рассмотрим частицу, пусть  - радиус-вектор, характеризующий ее положение относительно некоторой точки
- радиус-вектор, характеризующий ее положение относительно некоторой точки  выбранной системы отсчета, а
выбранной системы отсчета, а 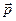 - ее импульс в этой системе.
- ее импульс в этой системе.
Моментом импульса частицы  относительно точки
относительно точки  (рисунок 7.1) называют вектор
(рисунок 7.1) называют вектор  , равный векторному произведению векторов
, равный векторному произведению векторов  и
и 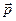 :
:
 (7.1)
(7.1)
Из этого определения следует, что  является аксиальным вектором. Его направление выбрано так, что вращение вокруг точки
является аксиальным вектором. Его направление выбрано так, что вращение вокруг точки  в направлении
в направлении
Рисунок 7.1
вектора 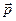 и вектор
и вектор  образуют правовинтовую систему. Модуль вектора
образуют правовинтовую систему. Модуль вектора  равен
равен
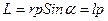 , (7.2)
, (7.2)
где 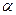 - угол между
- угол между  и
и 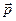 ,
, 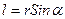 - плечо вектора
- плечо вектора 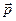 относительно точки
относительно точки  (рисунок 7.1).
(рисунок 7.1).
Чтобы выяснить, какая величина отвечает за изменение момента импульса частицы, продифференцируем выражение (7.1) по времени:
 .
.
Так как точка  неподвижна, то вектор
неподвижна, то вектор  равен скорости
равен скорости  частицы, т.е. совпадает по направлению с вектором
частицы, т.е. совпадает по направлению с вектором 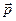 , поэтому
, поэтому
 .
.
Согласно второму закону Ньютона, 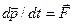 , где
, где 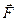 - равнодействующая всех сил, приложенных к частице. Следовательно,
- равнодействующая всех сил, приложенных к частице. Следовательно,
 .
.
Величина, стоящая в правой части последнего уравнения есть момент силы 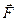 относительно точки
относительно точки  .
.
Таким образом, получаем уравнение моментов:
 . (7.3)
. (7.3)
Уравнение моментов позволяет получить ответ на два вопроса:
1) найти момент силы  относительно интересующей точки
относительно интересующей точки  в любой момент времени
в любой момент времени  , если известна зависимость от времени момента импульса
, если известна зависимость от времени момента импульса 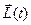 частицы, относительно той же точки;
частицы, относительно той же точки;
2)определить приращение момента импульса частицы относительно точки  за любой промежуток времени, если известна зависимость от времени момента силы
за любой промежуток времени, если известна зависимость от времени момента силы 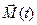 , действующего на эту частицу (относительно той же точки
, действующего на эту частицу (относительно той же точки  ).
).
Решение первого вопроса сводится к нахождению производной по времени от момента импульса, решение второго – к интегрированию уравнения (7.3):
 (7.4)
(7.4)
Величину, стоящую в правой части этого уравнения, называют импульсом момента силы. Таким образом, приращение момента импульса частицы за любой промежуток времени равно импульсу момента силы за это же время.
Возьмем в интересующей нас системе отсчета произвольную неподвижную ось  . Пусть относительно некоторой точки
. Пусть относительно некоторой точки  на оси
на оси  момент импульса частицы
момент импульса частицы  равен
равен  .
.
Моментом импульса относительно оси  называют проекцию на эту ось вектора
называют проекцию на эту ось вектора  , определенного относительно произвольной точки
, определенного относительно произвольной точки  данной оси и обозначают
данной оси и обозначают 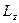 .Нахождение аналитического выражения для
.Нахождение аналитического выражения для 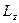 сводится к нахождению проекций на ось
сводится к нахождению проекций на ось  векторного произведения
векторного произведения  .
.
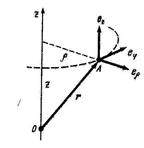 Воспользуемся цилиндрической системой координат
Воспользуемся цилиндрической системой координат 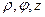 , связав с частицей
, связав с частицей  (рисунок 7.2) орты
(рисунок 7.2) орты 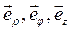 ,направленные в сторону возрастания соответствующих координат. В данной системе координат радиус-вектор
,направленные в сторону возрастания соответствующих координат. В данной системе координат радиус-вектор  и импульс
и импульс 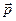 частицы записывают так:
частицы записывают так:
 ,
,
где  - проекции вектора
- проекции вектора 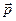 на соответствующие орты.
на соответствующие орты.
Рисунок 7.2
Из векторной алгебры известно, что векторное произведение  можно представить определителем
можно представить определителем
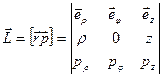
откуда сразу видно, что момент импульса частицы относительно оси 
 , (7.5)
, (7.5)
где 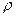 - расстояние частицы от оси
- расстояние частицы от оси  . Имея в виду, что
. Имея в виду, что 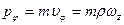 , получаем
, получаем
 , (7.6)
, (7.6)
где 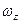 - проекция угловой скорости, с которой поворачивается радиус-вектор частицы.
- проекция угловой скорости, с которой поворачивается радиус-вектор частицы.
Закон сохранения момента импульса. Выберем произвольную систему частиц. Момент импульса данной системы частиц можно представить как векторную сумму моментов импульсов ее отдельных частиц:
 , (7.7)
, (7.7)
где все векторы определены относительно одной и той же точки  заданной системы отсчета. Заметим, что момент импульса системы – величина аддитивная: момент импульса системы равен сумме моментов импульсов ее отдельных частей независимо от того, взаимодействуют они между собой или нет.
заданной системы отсчета. Заметим, что момент импульса системы – величина аддитивная: момент импульса системы равен сумме моментов импульсов ее отдельных частей независимо от того, взаимодействуют они между собой или нет.
Продифференцируем уравнение (7.7) по времени и представим момент всех сил, действующих на частицу в виде суммы моментов внутренних и внешних сил, т.е.  , получим:
, получим:
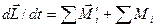 .
.
Здесь первая сумма – это суммарный момент всех внутренних сил относительно точки  , вторая сумма – суммарный момент всех внешних сил относительно той же точки
, вторая сумма – суммарный момент всех внешних сил относительно той же точки  .
.
Суммарный момент всех внутренних сил относительно любой точки равен нулю. Действительно, внутренние силы – это силы взаимодействия между частицами данной системы. По третьему закону Ньютона, эти силы попарно одинаковы по модулю, противоположны по направлению и лежат на одной прямой, т.е. имеют одинаковое плечо. Поэтому моменты каждой пары взаимодействия равны по модулю и противоположны по направлению, т.е. уравновешивают друг друга, а, значит,  .
.
В результате последнее выражение принимает вид
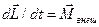 (7.8)
(7.8)
где 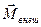 - суммарный момент всех внешних сил. Уравнение (7.8) утверждает: производная момента импульса системы по времени равна суммарному моменту всех внешних сил. Т.е. момент импульса системы может меняться под действием только суммарного момента всех внешних сил. Отсюда вытекает другое важное утверждение – закон сохранения момента импульса:момент импульса замкнутой системы частиц остается постоянным, т.е. не меняется со временем относительно любой точки инерциальной системы отсчета:
- суммарный момент всех внешних сил. Уравнение (7.8) утверждает: производная момента импульса системы по времени равна суммарному моменту всех внешних сил. Т.е. момент импульса системы может меняться под действием только суммарного момента всех внешних сил. Отсюда вытекает другое важное утверждение – закон сохранения момента импульса:момент импульса замкнутой системы частиц остается постоянным, т.е. не меняется со временем относительно любой точки инерциальной системы отсчета:
 . (7.9)
. (7.9)
Поучительные демонстрационные опыты на закон сохранения момента импульса можно осуществить с помощью скамьи Жуковского. Скамья Жуковского представляет собой угол, сидение которого имеет форму диска. Диск может свободно вращаться вокруг вертикальной оси на шариковых подшипниках. Во время опыта демонстратор садится или становится на скамью Жуковского и, отталкиваясь от пола, может приводить ее во вращение. После прекращения толчка единственными внешними силами, которые могут создавать момент относительно оси вращения, являются силы трения и сопротивления воздуха. Силы трения благодаря шариковым подшипникам очень малы, а сопротивление воздуха можно не принимать во внимание, пока число оборотов скамьи мало. Поэтому момент импульса системы, состоящей из скамьи и демонстратора, относительно оси вращения не может  меняться во времени, если система предоставлена самой себе. Какие бы внутренние движения ни совершались в системе – внутренние движения не могут изменить вращательный импульс. Если демонстратор разведет руки в стороны, то он увеличит момент инерции системы
меняться во времени, если система предоставлена самой себе. Какие бы внутренние движения ни совершались в системе – внутренние движения не могут изменить вращательный импульс. Если демонстратор разведет руки в стороны, то он увеличит момент инерции системы  , а потому угловая скорость вращения
, а потому угловая скорость вращения 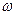 должна уменьшится, чтобы остался неизменным вращательный импульс
должна уменьшится, чтобы остался неизменным вращательный импульс 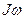 . Если демонстратор сводит руки к оси вращения, то момент инерции уменьшается, а угловая скорость увеличивается.
. Если демонстратор сводит руки к оси вращения, то момент инерции уменьшается, а угловая скорость увеличивается.
Рисунок 7.3
С помощью скамьи Жуковского можно демонстрировать и векторный характер момента импульса. Для этой цели применяется велосипедное колесо с утяжеленным ободом. Если колесо вращается вокруг собственной оси, то вследствие осевой симметрии полный импульс его 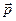 равен нулю. В этом случае момент импульса
равен нулю. В этом случае момент импульса  относительно неподвижной точки не зависит от положения этой точки. С другой стороны, проекция вектора
относительно неподвижной точки не зависит от положения этой точки. С другой стороны, проекция вектора  на ось вращения колеса равна
на ось вращения колеса равна  , где
, где  - момент инерции колеса, а
- момент инерции колеса, а  - его угловая скорость. Проекция вектора
- его угловая скорость. Проекция вектора  на любое направление, перпендикулярное к оси колеса, равно нулю ввиду осевой симметрии. Отсюда следует, что вектор момента импульса
на любое направление, перпендикулярное к оси колеса, равно нулю ввиду осевой симметрии. Отсюда следует, что вектор момента импульса  направлен вдоль оси колеса и по модулю равен
направлен вдоль оси колеса и по модулю равен  .
.



Рисунок 7.4
Демонстратор садится или становится на скамью Жуковского. Ему передают быстро вращающееся колесо с вертикально направленной осью (рисунок 7.4). Полный момент импульса системы направлен вертикально и равен  . Примем вертикальную ось скамьи Жуковского за ось
. Примем вертикальную ось скамьи Жуковского за ось 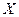 . Так как момент внешних сил относительно оси
. Так как момент внешних сил относительно оси 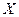 равен нулю, то проекция
равен нулю, то проекция 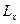 полного момента импульса системы на эту ось должна сохраняться. В начале опыта весь вращательный импульс сосредоточен в колесе. Затем демонстратор наклоняет ось колеса на угол
полного момента импульса системы на эту ось должна сохраняться. В начале опыта весь вращательный импульс сосредоточен в колесе. Затем демонстратор наклоняет ось колеса на угол 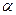 . Проекция момента импульса колеса на ось
. Проекция момента импульса колеса на ось 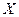 становится равной
становится равной 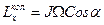 , т.е. она уменьшается на
, т.е. она уменьшается на  . Это уменьшение должно быть скомпенсировано возрастанием соответствующей проекции момента импульса скамьи и демонстратора на величину
. Это уменьшение должно быть скомпенсировано возрастанием соответствующей проекции момента импульса скамьи и демонстратора на величину  . В результате скамья с демонстратором приходит во вращение с угловой скоростью
. В результате скамья с демонстратором приходит во вращение с угловой скоростью  , определяемой из уравнения
, определяемой из уравнения  , где
, где 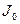 - момент инерции скамьи. При
- момент инерции скамьи. При 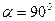 проекция
проекция  обращается в нуль – она целиком передается скамье и демонстратору. При
обращается в нуль – она целиком передается скамье и демонстратору. При  изменение вращательного импульса колеса становится максимальным
изменение вращательного импульса колеса становится максимальным 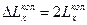 , скамья и демонстратор вращаются с максимальной скоростью
, скамья и демонстратор вращаются с максимальной скоростью  . Поворачивая ось, демонстратор придает ей исходное направление – тогда вращение скамьи прекращается.
. Поворачивая ось, демонстратор придает ей исходное направление – тогда вращение скамьи прекращается.
Экспериментальная часть
В эксперименте данной лабораторной работы используется система тел, у которой в процессе движения может меняться конфигурация и, следовательно, ее момент инерции.
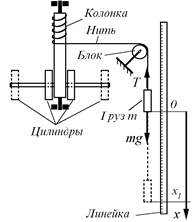 Механическая система представляет собой колонку с горизонтальным стержнем, по которому могут свободно перемещаться два цилиндра (рисунок 7.5). Эта колонка может вращаться вокруг своей оси. Для осуществления такого вращения на нее наматывается нить, переброшенная через дополнительный блок. На конце нити подвешен груз массы
Механическая система представляет собой колонку с горизонтальным стержнем, по которому могут свободно перемещаться два цилиндра (рисунок 7.5). Эта колонка может вращаться вокруг своей оси. Для осуществления такого вращения на нее наматывается нить, переброшенная через дополнительный блок. На конце нити подвешен груз массы 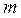 . В исходном состоянии эта нить намотана на колонку, груз находится в верхнем положении, а цилиндры удерживаются на минимальном расстоянии от оси. Для определенности выберем систему координат так, как показано на рисунке 7.5, совместив ее начало с положением груза в верхней точке.
. В исходном состоянии эта нить намотана на колонку, груз находится в верхнем положении, а цилиндры удерживаются на минимальном расстоянии от оси. Для определенности выберем систему координат так, как показано на рисунке 7.5, совместив ее начало с положением груза в верхней точке.
Рисунок 7.5 Все время движения рассматриваемой механической системы с меняющимся моментом инерции может быть разбито на три стадии. На первой, система, имея наименьший момент инерции, начинает вращаться с ускорением под действием момента силы натяжения нити, на которой подвешен груз 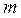 . На второй, когда груз полностью опускается (до координаты
. На второй, когда груз полностью опускается (до координаты 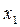 ), цилиндры освобождаются и меняют свое положение (на рисунке 7.5 новое положение цилиндров показано штриховыми линиями). Момент инерции системы тел в этой стадии быстро увеличивается и становится наибольшим, а угловая скорость вращения уменьшается. В третьей стадии система, имея наибольший момент инерции, вращается замедленно и останавливается. При этом груз
), цилиндры освобождаются и меняют свое положение (на рисунке 7.5 новое положение цилиндров показано штриховыми линиями). Момент инерции системы тел в этой стадии быстро увеличивается и становится наибольшим, а угловая скорость вращения уменьшается. В третьей стадии система, имея наибольший момент инерции, вращается замедленно и останавливается. При этом груз 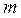 поднимется до координаты
поднимется до координаты  . Изменение угловой скорости вращения системы со временем может быть изображено примерно так, как показано на рисунке 7.6. Возрастающая ветвь от нуля до точки
. Изменение угловой скорости вращения системы со временем может быть изображено примерно так, как показано на рисунке 7.6. Возрастающая ветвь от нуля до точки  отвечает первой стадии. Убывающая ветвь, от точки
отвечает первой стадии. Убывающая ветвь, от точки 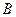 до точки
до точки 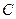 , отвечает третьей стадии. За незначительное время
, отвечает третьей стадии. За незначительное время  в интервале
в интервале 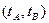 , угловая скорость быстро уменьшается. Участок кривой
, угловая скорость быстро уменьшается. Участок кривой 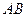 соответствует второй стадии, стадии увеличения момента инерции системы. В связи с тем, что время
соответствует второй стадии, стадии увеличения момента инерции системы. В связи с тем, что время  мало, момент силы натяжения нити за это время не успевает существенно вырасти от нулевого значения в момент
мало, момент силы натяжения нити за это время не успевает существенно вырасти от нулевого значения в момент 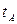 , и поэтому не успевает заметно изменить момент количества движения колонки.
, и поэтому не успевает заметно изменить момент количества движения колонки.
 Рисунок 7.6 - Зависимость угловой скорости колонки от времени
Рисунок 7.6 - Зависимость угловой скорости колонки от времени
|
Применяя к этой стадии закон сохранения момента количества движения, получим
 , (7.10)
, (7.10)
или
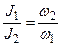 , (7.11)
, (7.11)
где 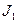 и
и 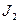 ¾ соответственно наименьший и наибольший моменты инерции системы,
¾ соответственно наименьший и наибольший моменты инерции системы,
 ¾ наибольшая угловая скорость на первой стадии движения,
¾ наибольшая угловая скорость на первой стадии движения,
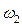 ¾ наибольшая угловая скорость в третьей стадии движения.
¾ наибольшая угловая скорость в третьей стадии движения.
Выразим величины, входящие в уравнения (7.10) и (7.11), через другие параметры системы с изменяющимся значением момента инерции. Для определения угловых скоростей вращения колонки  и
и 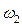 воспользуемся законом сохранения энергии. Потенциальную энергию груза при
воспользуемся законом сохранения энергии. Потенциальную энергию груза при 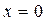 примем равной нулю. При опускании груза (при этом цилиндры находятся около колонки) имеем:
примем равной нулю. При опускании груза (при этом цилиндры находятся около колонки) имеем:
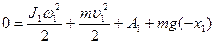 , (7.12)
, (7.12)
где 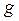 ¾ ускорение свободного падения,
¾ ускорение свободного падения,
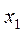 ¾ координата груза в нижней точке,
¾ координата груза в нижней точке,
 ¾ работа сил трения при опускании груза,
¾ работа сил трения при опускании груза,
 ¾ скорость груза в нижней точке, равная (
¾ скорость груза в нижней точке, равная ( ¾ радиус колонки),
¾ радиус колонки),
 ¾ кинетическая энергия вращения колонки в момент
¾ кинетическая энергия вращения колонки в момент 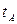 (рисунок 7.6).
(рисунок 7.6).
Из уравнения (7.12), с учетом 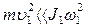 , получаем:
, получаем:
 . (7.13)
. (7.13)
После полного разматывания нити цилиндры переходят в крайние положения. Момент инерции колонки увеличивается и становится равным 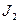 , угловая скорость вращения уменьшается и становится равной
, угловая скорость вращения уменьшается и становится равной 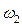 . При разлете цилиндров, во время их удара о крайние упоры часть механической энергии системы тел переходит в тепло, поэтому кинетическая энергия вращения
. При разлете цилиндров, во время их удара о крайние упоры часть механической энергии системы тел переходит в тепло, поэтому кинетическая энергия вращения 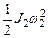 (в момент времени
(в момент времени 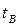 ) меньше. Закон изменения энергии на участке
) меньше. Закон изменения энергии на участке 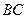 (см. рисунок 7.6) запишем в виде
(см. рисунок 7.6) запишем в виде
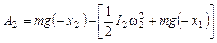 , (7.14)
, (7.14)
где 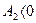 ¾ работа сил трения при подъеме груза.
¾ работа сил трения при подъеме груза.
Из последнего уравнения получим:
 . (7.15)
. (7.15)
Определение моментов инерции для двух конфигураций системы может быть осуществлено двумя способами. В первом фиксируют цилиндры в одном из положений и анализируют движение тел системы при опускании груза 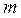 . При движении с неизменным наименьшим моментом инерции
. При движении с неизменным наименьшим моментом инерции 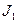 (цилиндры расположены вблизи оси колонки) имеем
(цилиндры расположены вблизи оси колонки) имеем
уравнение движения груза 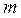
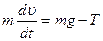 , (7.16)
, (7.16)
уравнение вращательного движения колонки
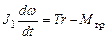 , (7.17)
, (7.17)
уравнение кинематической связи
 , (7.18)
, (7.18)
где  ¾ ускорение груза на нити,
¾ ускорение груза на нити,
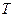 ¾ натяжение нити,
¾ натяжение нити,
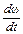 ¾ угловое ускорение системы,
¾ угловое ускорение системы,
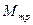 ¾ момент сил трения.
¾ момент сил трения.
Из уравнений (7.16), (7.17) и (7.18) имеем
 .
.
Предполагая, что  и
и  , получаем
, получаем
 .
.
В связи с тем, что движение груза равноускоренное,
 ,
,
где  ¾ время опускания груза в том случае, когда момент инерции колонки неизменен и равен
¾ время опускания груза в том случае, когда момент инерции колонки неизменен и равен 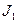 . Из двух последних уравнений получим
. Из двух последних уравнений получим
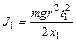 . (7.19)
. (7.19)
Аналогично при движении системы с неизменным наибольшим моментом инерции имеем
 , (7.20)
, (7.20)
где  ¾ время опускания груза на полную длину нити до отметки
¾ время опускания груза на полную длину нити до отметки 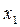 .
.
 Используя (7.13), (7.15), (7.19) и (7.20) можно проверить соотношение (7.10). При проверке закона сохранения момента количества движения с использованием соотношения (7.11) отношение моментов инерции
Используя (7.13), (7.15), (7.19) и (7.20) можно проверить соотношение (7.10). При проверке закона сохранения момента количества движения с использованием соотношения (7.11) отношение моментов инерции  можно найти, определяя периоды колебаний крутильного маятника, образованного колонкой с навитой нитью и двумя пружинками с коэффициентом жесткости
можно найти, определяя периоды колебаний крутильного маятника, образованного колонкой с навитой нитью и двумя пружинками с коэффициентом жесткости 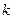 (рисунок 7.7).
(рисунок 7.7).
Рисунок 7.7 - Устройство
крутильного маятника
Периоды колебаний такого маятника легко получить, записав уравнение колебаний. Для моментов инерции 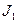 и
и 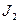 периоды колебаний равны соответственно
периоды колебаний равны соответственно
 и
и 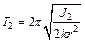 . (7.21)
. (7.21)
Как видим
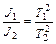 . (7.22)
. (7.22)
Экспериментальная установка
На диске имеются не указанные на рисунке специальные крепления. Ими можно закрепить, не пользуясь кольцом с нитями, цилиндры у поверхности колонки.…Проведение эксперимента
Моменты инерции и определяются по формулам (7.19) и (7.20) после экспериментального определения времен опускания груза и . Величины работи определяются экспериментально, исходя из следующих… , (7.23)Измерения
2 Провести измерения и . При измерениях цилиндры закрепляют у колонки. Навивают нить на колонку, подводя груз к нулю шкалы, останавливают его…Таблица 7.1
| i | |||||||||

| |||||||||
| t1 | |||||||||

| |||||||||
| x3 | |||||||||

| |||||||||
| t2 | |||||||||

| |||||||||
| x4 | |||||||||
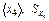
| |||||||||
| x2 | |||||||||
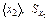
| |||||||||
3 Аналогично п.2 провести измерения  и
и  . Цилиндры в этом случае располагают в крайних, наиболее удаленных от оси положениях.
. Цилиндры в этом случае располагают в крайних, наиболее удаленных от оси положениях.
4 Провести измерения величины  т. е. координаты, до которой поднимется груз после изменения момента инерции системы. Для этого поступают следующим образом. Приблизив цилиндры к колонке, надевают пластинку кольца на конец стерженька фиксатора. Навивают виток к витку нить, соединенную с грузом, на колонку с пластинкой до тех пор, пока груз не будет на нулевой отметке шкалы. Останавливают возможные колебания груза. Освобождают колонку, после полного разматывания нити цилиндры освобождаются и переходят в положения, наиболее удаленные от оси. Отмечают положение груза на шкале
т. е. координаты, до которой поднимется груз после изменения момента инерции системы. Для этого поступают следующим образом. Приблизив цилиндры к колонке, надевают пластинку кольца на конец стерженька фиксатора. Навивают виток к витку нить, соединенную с грузом, на колонку с пластинкой до тех пор, пока груз не будет на нулевой отметке шкалы. Останавливают возможные колебания груза. Освобождают колонку, после полного разматывания нити цилиндры освобождаются и переходят в положения, наиболее удаленные от оси. Отмечают положение груза на шкале  , когда он, начав подниматься, вновь остановится. Измерение
, когда он, начав подниматься, вновь остановится. Измерение  производится 3–5 раз. Результаты измерений заносятся в таблицу 7.1.
производится 3–5 раз. Результаты измерений заносятся в таблицу 7.1.
Обработка результатов
1 По экспериментальным данным рассчитываются средние значения величин  (где j =2¾4) с использованием формулы[7]
(где j =2¾4) с использованием формулы[7]
 ,
,
где N ¾ число измерений. Аналогичные вычисления делаются и для  и
и  .
.
2 Вычислить выборочное стандартное отклонение
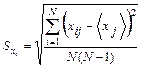 .
.
Результаты вычислений занести в таблицу 7.1.
3 С помощью формул (7.25) и (7.27) вычисляют значения 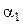 и
и  .
.
4 Произвести оценку погрешностей полученных значений 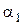 и
и  . В связи с тем, что измеряемая величина является косвенно измеряемой, то стандартное отклонение ошибок функции нескольких независимых переменных находится через соответствующие стандартные отклонения средних значений.
. В связи с тем, что измеряемая величина является косвенно измеряемой, то стандартное отклонение ошибок функции нескольких независимых переменных находится через соответствующие стандартные отклонения средних значений.

или
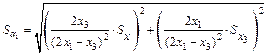
Аналогично для 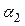 получаем
получаем
 .
.
Результаты вычислений 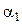 ,
, 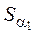 и
и  ,
, 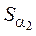 заносятся в таблицу 7.2.
заносятся в таблицу 7.2.
Таблица 7.2
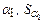
| 
| 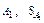
| 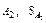
| 
| 
|
5 С помощью формул (7.23) и (7.28) определить величины работы 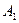 и
и 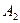 .
.
6 Провести оценку погрешностей  и
и  , используя методику, применяемую для определения погрешностей
, используя методику, применяемую для определения погрешностей 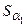 и
и 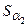 (см. п.4). Результаты вычислений А1,
(см. п.4). Результаты вычислений А1,  и A2,
и A2, 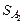 заносятся в таблицу 7.2.
заносятся в таблицу 7.2.
7 По формулам (7.19), (7.20) найти 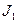 и
и 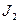 .
.
8 Провести оценку погрешностей 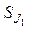 и
и 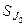 аналогично тому, как это делалось для
аналогично тому, как это делалось для 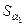 и
и 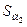 (в п. 4). Результаты вычислений заносятся в таблицу. 7.2.
(в п. 4). Результаты вычислений заносятся в таблицу. 7.2.
Упражнение 2. Определение отношения моментов инерции для двух конфигураций системы тел
Измерения
Таблица 7.3
| N | tn1 | 
| 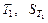
| tn2 | 
| 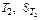
|
Обработка результатов
2 Найти выборочные стандартные отклонения и величин и . 3 Вычислить средние значения и их стандартные отклонения для периодов и : ,.Таблица 7.4
 , , 
|  , , 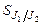
|
Упражнение 3. Определение моментов количества движения механической системы для двух положений цилиндров. Проверка закона сохранения момента количества движения.
В связи с тем, что для расчета моментов количества движения используются данные, полученные в упр.1 и упр.2, в данном упражнении осуществляется лишь обработка результатов.
1 С помощью формул (7.13) и (7.15) вычислить значения  и
и  , используя значения
, используя значения 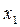 (таблица 7.1),
(таблица 7.1), 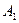 и
и 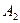 (таблица 7.2) и
(таблица 7.2) и 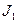 и
и 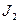 (таблица7.2).
(таблица7.2).
2 Произвести оценку погрешности полученных результатов по формулам для косвенных измерений. Результаты вычислений заносятся в таблицу 7.5.
Таблица 7.5

| 
| 
| 
| 
|
3 Вычислить моменты количества движения при двух положениях цилиндров  и
и 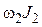 . Провести оценку погрешностей определения моментов количества движения. Результаты вычислений занести в таблицу 7.5.
. Провести оценку погрешностей определения моментов количества движения. Результаты вычислений занести в таблицу 7.5.
4 Вычислить отношение  . Провести оценку погрешностей этой величины. Результаты вычислений внести в таблицу 7.5.
. Провести оценку погрешностей этой величины. Результаты вычислений внести в таблицу 7.5.
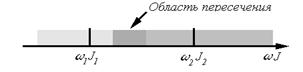 Рисунок 7.9 - Графическое представление результатов вычисления моментов количества движения для системы тел, исследуемых в работе
Рисунок 7.9 - Графическое представление результатов вычисления моментов количества движения для системы тел, исследуемых в работе
|
5 Провести сравнение экспериментально определенных значений моментов количества движения системы тел при двух ее конфигурациях. Для чего на оси значений 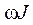 (см. рисунок 7.9) отметить значения
(см. рисунок 7.9) отметить значения 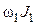 и
и  , а также их стандартные отклонения
, а также их стандартные отклонения 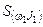 и
и  (см. рисунок 7.9). На рисунке 7.9 области
(см. рисунок 7.9). На рисунке 7.9 области 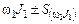 и
и  имеют различную штриховку. Пересечение этих областей указывает на выполнимость закона сохранения момента количества движения.
имеют различную штриховку. Пересечение этих областей указывает на выполнимость закона сохранения момента количества движения.
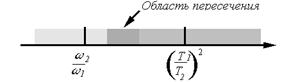 Рисунок 7.10 - Схематическое представление выполнимости закона сохранения моментов количества движения для системы тел, исследуемых в работе
Рисунок 7.10 - Схематическое представление выполнимости закона сохранения моментов количества движения для системы тел, исследуемых в работе
|
6 Выполнимость закона сохранения момента количества движения cогласно (7.11) также следует из равенства отношений  и
и 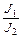 . Поэтому необходимо провести сравнение экспериментально определенных значений этих отношений. Для этого на оси численных значений (см. рисунок 7.10) отметить значения
. Поэтому необходимо провести сравнение экспериментально определенных значений этих отношений. Для этого на оси численных значений (см. рисунок 7.10) отметить значения  и
и 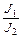 , взятые из таблицы 7.4, а также их стандартные отклонения (см. рисунок 7.10). Пересечение этих областей указывает на выполнимость закона сохранения момента количества движения.
, взятые из таблицы 7.4, а также их стандартные отклонения (см. рисунок 7.10). Пересечение этих областей указывает на выполнимость закона сохранения момента количества движения.
Основные итоги работы
7.3 Контрольные вопросы:Рекомендуемая литература
7.4.1 Зисман, Г.А. Курс общей физики: в 3 т. / Г.А. Зисман, О.М. Тодес. – СПб.: Лань, 2007. – Т.1: Механика. Молекулярная физика. Колебания и волны. – 340 с. - ISBN 978-5-8114-0753-8.
7.4.2 Иродов, И.Е. Механика. Основные законы механики / И.Е.Иродов. - М.: Бином, 2009. – 310 с. - ISBN 978-5-9963-0063-1.
7.4.3 Матвеев, А.Н. Механика и теория относительности / А.Н. Матвеев. – М.: Высш. шк., 1986. – 320 с.
7.4.4 Савельев, И.В. Курс общей физики: в 5 кн. / И.В.Савельев. – М.: АСТРЕЛЬ: АСТ, 2005. – Кн. 1: Механика. – 336 с. - ISBN 5-271-01034-1.
7.4.4 Сивухин, Д.В. Общий курс физики: в 3 т. / Д.В.Сивухин. - М.: Физматлит, 2002. – Т. 1: Механика. – 560 с. - ISBN 5-89155-078-4.
7.4.6 Трофимова, Т.И. Физика в таблицах и формулах / Т.И. Трофимова. – М.: Академия, 2006. – 448 с. - ISBN 5-7695-2277-1.
Лабораторная работа №8. Изучение деформации растяжения и сжатия
Цель работы: 1) изучение теории деформаций.
2) изучение деформаций растяжения и изгиба.
3) экспериментальное определение модуля Юнга для нескольких материалов.
Теоретическая часть
Все реальные тела деформируемы. Под действием приложенных сил они меняют свою форму или объем. Такие изменения называются деформациями. В случае твердых тел различают два предельных случая: деформации упругие и деформации пластические. Упругими называют деформации, исчезающие после прекращения действия приложенных сил. Пластическими или остаточными деформациями называют такие деформации, которые сохраняются в теле, по крайней мере частично, и после прекращения действия внешних приложенных сил. На пластических деформациях основана холодная обработка металлов — штамповка, ковка и пр. Является ли деформация упругой или пластической зависит не только от материала тела, но и от приложенных сил. Если сила (точнее, сила, отнесенная к единице площади, т. е. напряжение) не превосходит известной величины, называемой пределом упругости, то возникающая деформация будет упругой. Если же она превосходит этот предел, то возникающая деформация будет пластической. Предел упругости имеет различные значения для разных материалов.
Механика описывает упругие свойства тел посредством некоторых эмпирически вводимых упругих постоянных, различных для различных тел и зависящих от их физического состояния (например, от температуры). Более глубоким является физический подход, рассматривающий явление деформаций с атомистической точки зрения. Этим занимается теория твердого тела. Она позволяет в принципе не только вывести основные уравнения механики деформируемых тел с атомистической точки зрения, но и установить связь между упругими постоянными вещества и другими его физическими свойствами.
Тела мы будем считать идеально упругими. Так называются идеализированные тела, которые могут претерпевать только упругие, но не пластические деформации. Такими идеализациями можно пользоваться, когда силы, приложенные к реальным телам, не превосходят предела упругости. Для идеально упругих тел существует однозначная зависимость между действующими силами и вызываемыми ими деформациями. Для малых деформаций справедлив закон Гука. Это приближенный закон, согласно которому деформации пропорциональны силам, их вызывающим.
Твердые тела разделяются на изотропные и анизотропные. Изотропными называются тела, свойства которых по всем направлениям одинаковы. Анизотропными называются тела, свойства которых в разных направлениях не одинаковы. Типичными представителями анизотропных тел являются кристаллы. Металлы обычно имеют поликристаллическую структуру, т. е. состоят из мельчайших беспорядочно ориентированных кристалликов. Каждый из таких кристалликов есть тело анизотропное. Но кусочек металла, содержащий множество их, ведет себя как изотропное тело, если всевозможные ориентации кристалликов представлены с одинаковой вероятностью. В результате пластической деформации хаотичность в ориентации кристалликов может нарушиться. Тогда после пластической деформации металл становится анизотропным. Такое явление наблюдается, например, при вытягивании или кручении проволоки.

 Рассмотрим однородный стержень и приложим к его основаниям растягивающие или сжимающие силы
Рассмотрим однородный стержень и приложим к его основаниям растягивающие или сжимающие силы  . Стержень будет деформирован, т. е. растянут или сжат. Мысленно проведем произвольное сечение
. Стержень будет деформирован, т. е. растянут или сжат. Мысленно проведем произвольное сечение 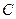 , перпендикулярное к оси стержня. Для равновесия стержня
, перпендикулярное к оси стержня. Для равновесия стержня  необходимо, чтобы на его нижнее основание
необходимо, чтобы на его нижнее основание 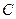 действовала сила
действовала сила 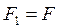 . Это есть сила, с которой нижняя часть стержня
. Это есть сила, с которой нижняя часть стержня 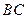 тянет верхнюю или давит на нее. Такая сила возникает потому, что нижняя часть стержня деформирована. Верхняя часть стержня также деформирована и действует на нижнюю с силой, равной
тянет верхнюю или давит на нее. Такая сила возникает потому, что нижняя часть стержня деформирована. Верхняя часть стержня также деформирована и действует на нижнюю с силой, равной 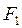 противоположно направленной. Такие силы действуют в любом поперечном сечении растянутого или сжатого стержня. Таким образом, деформация стержня связана с возникновением упругих сил, с которыми каждая часть стержня действует на другую, с которой она граничит. Силу, отнесенную к единице площади поперечного сечения стержня, называют напряжением. В рассматриваемом случае напряжение перпендикулярно к поперечному сечению стержня. Если стержень растянут, то это напряжение называется натяжением и определяется выражением
противоположно направленной. Такие силы действуют в любом поперечном сечении растянутого или сжатого стержня. Таким образом, деформация стержня связана с возникновением упругих сил, с которыми каждая часть стержня действует на другую, с которой она граничит. Силу, отнесенную к единице площади поперечного сечения стержня, называют напряжением. В рассматриваемом случае напряжение перпендикулярно к поперечному сечению стержня. Если стержень растянут, то это напряжение называется натяжением и определяется выражением
 ,
,
где  — площадь поперечного сечения стержня. Если же стержень сжат, то напряжение называется давлением и численно определяется той же формулой
— площадь поперечного сечения стержня. Если же стержень сжат, то напряжение называется давлением и численно определяется той же формулой
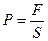 .
.
Давление можно рассматривать как отрицательное натяжение и наоборот, т. е.
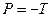 .
.
Это замечание освобождает от необходимости рассматривать отдельно растяжение и сжатие.
Пусть  — длина недеформированного стержня. После приложения силы
— длина недеформированного стержня. После приложения силы  его длина получает приращение
его длина получает приращение  и делается равной
и делается равной  . Отношение
. Отношение

называется относительным удлинением стержня. В случае растягивающих сил оно положительно, в случае сжимающих сил — отрицательно. Относительное удлинение, взятое с противоположным знаком, называется относительным сжатием.
Опыт показывает, что для не слишком больших упругих деформаций натяжение 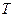 (или давление
(или давление  ) пропорционально относительному удлинению (или относительному сжатию)
) пропорционально относительному удлинению (или относительному сжатию)
 или
или  , (8.1)
, (8.1)
где  — постоянная, зависящая только от материала стержня и его физического состояния - модуль Юнга.
— постоянная, зависящая только от материала стержня и его физического состояния - модуль Юнга.
Формулы (8.1) выражают закон Гука для деформаций растяжения и сжатия стержней. Это приближенный закон. Для больших деформаций он может не оправдываться.
Более общим, чем закон Гука, является утверждение, что в случае упругих деформаций натяжение 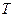 является однозначной функцией относительного удлинения
является однозначной функцией относительного удлинения  :
: 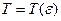 . Эта функция должна обращаться в нуль при
. Эта функция должна обращаться в нуль при  , так как с исчезновением деформации
, так как с исчезновением деформации  исчезает и напряжение
исчезает и напряжение 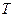 . Поэтому в разложении функции
. Поэтому в разложении функции 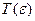 в ряд по степеням
в ряд по степеням  должен отсутствовать нулевой член. Это разложение должно иметь вид
должен отсутствовать нулевой член. Это разложение должно иметь вид
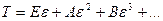 ,
,
причем коэффициенты  являются постоянными, зависящими только от материала стержня и его физического состояния. Если относительное удлинение
являются постоянными, зависящими только от материала стержня и его физического состояния. Если относительное удлинение  мало, то высшими степенями
мало, то высшими степенями  можно пренебречь. Тогда мы придем к закону Гука (8.1).
можно пренебречь. Тогда мы придем к закону Гука (8.1).
Если деформации малы, то упругие постоянные тел не изменяются при деформациях. Отсюда следует, что если на тело действует несколько сил, то для вычисления результирующей деформации можно вычислить сначала деформации, вызываемые каждой силой в отдельности (как если бы остальных сил не было вовсе), а затем полученные деформации сложить. Это важное положение называется принципом суперпозиции малых деформаций.
Для того чтобы деформировать тело, над ним надо совершить работу. В свою очередь, деформированное тело само может совершать работу. Оно обладает запасом потенциальной энергии. Эта энергия называется упругой. Она равна работе сил, затраченной на деформацию тела, при том существенном условии, что вся эта работа тратится только на приращение упругой энергии тела и не расходуется на увеличение кинетической энергии. Для того чтобы кинетическая энергия при деформации не возникала, надо деформацию производить достаточно медленно, постепенно увеличивая внешние силы, чтобы в любой момент времени каждая часть тела практически находилась в состоянии равновесия. Иначе говоря, при деформации внешние силы все время должны уравновешиваться возникающими при этом силами внутренних напряжений. Если это условие выполнено, то говорят, что тело совершает квазистатический процесс.
Приложим к стержню растягивающую силу  и будем непрерывно и медленно увеличивать ее от начального значения
и будем непрерывно и медленно увеличивать ее от начального значения  до конечного значения
до конечного значения 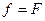 . При этом удлинение стержня будет меняться от
. При этом удлинение стержня будет меняться от  до конечного значения
до конечного значения 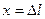 . По закону Гука
. По закону Гука  , где
, где 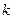 — коэффициент упругости. Вся работа в рассматриваемом процессе пойдет на приращение упругой энергии
— коэффициент упругости. Вся работа в рассматриваемом процессе пойдет на приращение упругой энергии  , а потому
, а потому
 . (8.2)
. (8.2)
Так как в конечном состоянии 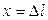 , то
, то 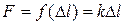 . Учитывая это, получим
. Учитывая это, получим

 . (8.3)
. (8.3)
Если бы к недеформированному стержню мы сразу приложили постоянную силу  , то при удлинении его на
, то при удлинении его на  была бы совершена вдвое большая работа
была бы совершена вдвое большая работа 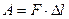 . Так как запас упругой потенциальной энергии в стержне получился бы тем же самым, то ясно, что только половина работы
. Так как запас упругой потенциальной энергии в стержне получился бы тем же самым, то ясно, что только половина работы  расходуется на приращение упругой энергии стержня. Вторая половина этой работы тратится на кинетическую энергию упругих колебаний и волн, которые всегда возбуждаются в стержне при неквазистатическом воздействии на него. При квазистатическом воздействии колебания и волны не возникают. Вот почему в формулах (8.2) и (8.3) появился числовой коэффициент 1/2.
расходуется на приращение упругой энергии стержня. Вторая половина этой работы тратится на кинетическую энергию упругих колебаний и волн, которые всегда возбуждаются в стержне при неквазистатическом воздействии на него. При квазистатическом воздействии колебания и волны не возникают. Вот почему в формулах (8.2) и (8.3) появился числовой коэффициент 1/2.
Найдем объемную плотность упругой энергии, т. е. упругую энергию, и приходящуюся на единицу объема растянутого (или сжатого) стержня. Она найдется делением выражения (8.3) на объем стержня 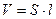 . Это дает
. Это дает
 . (8.4)
. (8.4)
Если воспользоваться законом Гука, то эту формулу нетрудно привести к виду
 . (8.5)
. (8.5)
Опыт показывает, что под действием растягивающей или сжимающей силы изменяются не только продольные, но и поперечные размеры стержня. Если сила
изменяются не только продольные, но и поперечные размеры стержня. Если сила  — растягивающая, то поперечные размеры стержня уменьшаются. Если она сжимающая, то они увеличиваются. Пусть
— растягивающая, то поперечные размеры стержня уменьшаются. Если она сжимающая, то они увеличиваются. Пусть 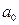 — толщина стержня до деформации,
— толщина стержня до деформации,  — после деформации. За толщину можно принять для круглого стержня его диаметр, для прямоугольного — одну из сторон его прямоугольного основания и т. д. Если сила
— после деформации. За толщину можно принять для круглого стержня его диаметр, для прямоугольного — одну из сторон его прямоугольного основания и т. д. Если сила  — растягивающая, то величина -
— растягивающая, то величина -  называется относительным поперечным сжатием стержня (
называется относительным поперечным сжатием стержня (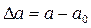 ). Отношение относительного поперечного сжатия к соответствующему относительному продольному удлинению называется коэффициентом Пуассона по имени французского ученого Симеона Пуассона (1781 — 1840):
). Отношение относительного поперечного сжатия к соответствующему относительному продольному удлинению называется коэффициентом Пуассона по имени французского ученого Симеона Пуассона (1781 — 1840):
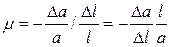 . (8.6)
. (8.6)
Коэффициент Пуассона зависит только от материала тела и является одной из важных постоянных, характеризующих его упругие свойства. Случай сжимающих сил не обязательно выделять особо так как сжимающую силу можно рассматривать как растягивающую, взятую с противоположным знаком.
Модуль Юнга Е и коэффициент Пуассона µ полностью характеризуют упругие свойства изотропного материала. Все прочие упругие постоянные могут быть выражены через  и
и  .
.
Заметим, наконец, что все модули и коэффициенты упругости, с которыми мы имели и будем иметь дело, следовало бы для точности называть изотермическими модулями и коэффициентами. Они характеризуют деформации тел в предположении, что температура их поддерживается постоянной. Это обычно имеет место в случае статических деформаций. Но если деформации динамические (например, волны в упругих средах), то они могут происходить настолько быстро, что разности температур, возникшие при деформации, не успевают выравниваться в результате теплообмена. Важнейшим является предельный случай, когда между различно нагретыми частями среды теплообмен совсем не происходит. Соответствующие процессы, модули и коэффициенты упругости называются адиабатическими.
Рассмотрим изгиб однородного бруса (балки) произвольного поперечного сечения, которое, однако, должно оставаться одинаковым на протяжении всей длины бруса. Пусть до деформации брус имел прямолинейную форму. Проведя сечения 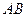 и
и  , нормальные к оси бруса, мысленно вырежем из него бесконечно малый элемент
, нормальные к оси бруса, мысленно вырежем из него бесконечно малый элемент 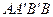 (рисунок 8.2,а), длину которого обозначим через
(рисунок 8.2,а), длину которого обозначим через  . Ввиду бесконечной малости выделенного элемента можно считать, что в результате изгиба прямые
. Ввиду бесконечной малости выделенного элемента можно считать, что в результате изгиба прямые 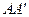 ,
,  ,
, и все прямые им параллельные, перейдут в дуги окружности с центрами, лежащими на оси
и все прямые им параллельные, перейдут в дуги окружности с центрами, лежащими на оси  , перпендикулярной к
, перпендикулярной к  плоскости рисунка (рисунок 8.2,б). Эта ось называется осью изгиба. Наружные волокна, лежащие выше линии
плоскости рисунка (рисунок 8.2,б). Эта ось называется осью изгиба. Наружные волокна, лежащие выше линии  , при изгибе удлиняются, волокна, лежащие ниже линии
, при изгибе удлиняются, волокна, лежащие ниже линии  , укорачиваются. Длина линии
, укорачиваются. Длина линии  остается
остается  неизменной. Эта линия называется нейтральной линией. Проходящее через нее сечение (недеформированного) бруса плоскостью, перпендикулярной к плоскости рисунка 8.2,а, называется нейтральным сечением. Таким образом, все наружные волокна будут растянуты, все внутренние — сжаты. Пусть
неизменной. Эта линия называется нейтральной линией. Проходящее через нее сечение (недеформированного) бруса плоскостью, перпендикулярной к плоскости рисунка 8.2,а, называется нейтральным сечением. Таким образом, все наружные волокна будут растянуты, все внутренние — сжаты. Пусть 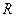 — радиус кривизны нейтральной линии
— радиус кривизны нейтральной линии  . Тогда
. Тогда 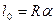 , где
, где 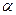 — центральный угол, опирающийся на дугу
— центральный угол, опирающийся на дугу  . Рассмотрим волокно бруса, находящегося на расстоянии
. Рассмотрим волокно бруса, находящегося на расстоянии  от нейтрального сечения. (Величина
от нейтрального сечения. (Величина  положительна, если волокно находится выше нейтрального сечения (рисунок 8.2,б), и отрицательна, если оно находится ниже.) Если брус не слишком толст, так что
положительна, если волокно находится выше нейтрального сечения (рисунок 8.2,б), и отрицательна, если оно находится ниже.) Если брус не слишком толст, так что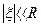 , то длина рассматриваемого волокна будет
, то длина рассматриваемого волокна будет 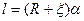 , а удлинение
, а удлинение  . Следовательно, натяжение, действующее вдоль рассматриваемого волокна,
. Следовательно, натяжение, действующее вдоль рассматриваемого волокна, 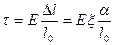 , или
, или
 . (8.7)
. (8.7)
Натяжение, таким образом, меняется линейно с расстоянием  . Ниже нейтрального сечения оно отрицательно, т. е. является давлением. Сумма сил натяжения и давления, действующих в сечении
. Ниже нейтрального сечения оно отрицательно, т. е. является давлением. Сумма сил натяжения и давления, действующих в сечении  , может быть и отличной от нуля. Однако в этом случае на изгиб бруса будет накладываться растяжение или сжатие его, одинаковое для всех волокон. Оно может быть учтено особо и исключено из рассмотрения, когда речь идет об изгибе в чистом виде. Поэтому мы будем считать, что сумма всех сил натяжения, действующих в каждом нормальном сечении бруса, равна нулю, т. е.
, может быть и отличной от нуля. Однако в этом случае на изгиб бруса будет накладываться растяжение или сжатие его, одинаковое для всех волокон. Оно может быть учтено особо и исключено из рассмотрения, когда речь идет об изгибе в чистом виде. Поэтому мы будем считать, что сумма всех сил натяжения, действующих в каждом нормальном сечении бруса, равна нулю, т. е.  или в силу (8.7)
или в силу (8.7) 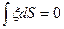 , где
, где  — элемент площади рассматриваемого поперечного сечения. Интегрирование ведется по всему поперечному сечению бруса. Отсюда видно, что нейтральная линия и нейтральное сечение проходят через центр тяжести поперечного сечения бруса. Из соотношения
— элемент площади рассматриваемого поперечного сечения. Интегрирование ведется по всему поперечному сечению бруса. Отсюда видно, что нейтральная линия и нейтральное сечение проходят через центр тяжести поперечного сечения бруса. Из соотношения  следует, что момент сил натяжения
следует, что момент сил натяжения 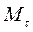 , действующих на сечение
, действующих на сечение , не зависит от того, относительно какой оси он берется. Для вычисления
, не зависит от того, относительно какой оси он берется. Для вычисления 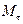 проще всего взять ось, перпендикулярную к плоскости рисунка и проходящую через точку
проще всего взять ось, перпендикулярную к плоскости рисунка и проходящую через точку 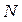 . Очевидно,
. Очевидно,
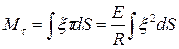 ,
,
или
 , (8.8)
, (8.8)
где введено обозначение
 (8.9)
(8.9)
Величина  называется моментом инерции поперечного сечения бруса по аналогии с соответствующей величиной, вводимой при рассмотрении вращения тела вокруг неподвижной оси. Однако в отличие от последней величины, имеющей размерность массы, умноженной на квадрат длины, (8.9) есть чисто геометрическая величина с размерностью четвертой степени длины.
называется моментом инерции поперечного сечения бруса по аналогии с соответствующей величиной, вводимой при рассмотрении вращения тела вокруг неподвижной оси. Однако в отличие от последней величины, имеющей размерность массы, умноженной на квадрат длины, (8.9) есть чисто геометрическая величина с размерностью четвертой степени длины.
Можно воспользоваться формулами для моментов инерции, заменив всюду массу 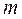 на площадь поперечного сечения
на площадь поперечного сечения  (рисунок 8.3). Если поперечное сечение бруса имеет форму прямоугольника с шириной
(рисунок 8.3). Если поперечное сечение бруса имеет форму прямоугольника с шириной 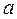 и высотой
и высотой 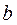 (рисунок 8.3,а), то
(рисунок 8.3,а), то
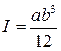 . (8.10)
. (8.10)
Для кругового поперечного сечения радиуса 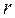 (рисунок 8.3,б)
(рисунок 8.3,б)
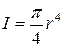 . (8.11)
. (8.11)
Для цилиндрической трубы с внутренним диаметром и наружным
и наружным 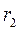 (рисунок 8.3,в)
(рисунок 8.3,в)
 . (8.12)
. (8.12)
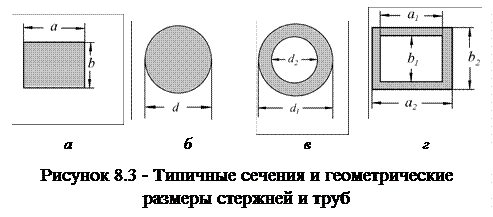
Для трубы с прямоугольным сечением (рисунок 8.3,г)
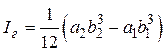 . (8.13)
. (8.13)
Направим ось 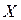 вдоль нейтральной линии недеформированного бруса. Ось
вдоль нейтральной линии недеформированного бруса. Ось  направим к ней перпендикулярно и расположим в плоскости изгиба. Тогда уравнение нейтральной линии изогнутого бруса можно представить в виде
направим к ней перпендикулярно и расположим в плоскости изгиба. Тогда уравнение нейтральной линии изогнутого бруса можно представить в виде 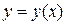 . По известной формуле
. По известной формуле
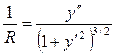 .
.
Если изгиб мал ( ), то квадратом производной можно пренебречь. В этом приближении
), то квадратом производной можно пренебречь. В этом приближении
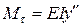 .
.
Рассмотрим прямой упругий стержень, неподвижно закрепленный одним концом в твердой стенке, а к другому его концу приложена сила  (рисунок 8.4,а). Стержень согнется.
(рисунок 8.4,а). Стержень согнется.
Перемещение  , которое получает свободный конец стержня, называется стрелой прогиба. Стрела прогиба тем больше, чем больше нагрузка, и, кроме того, зависит от формы стержня, его размеров и модуля упругости. Точный анализ деформаций и напряжений в упругом стержне довольно сложен. Приближенные результаты можно получить, используя так называемую гипотезу Бернулли о том, что в каждом малом объеме стержня происходит только деформация сжатия или растяжения.
, которое получает свободный конец стержня, называется стрелой прогиба. Стрела прогиба тем больше, чем больше нагрузка, и, кроме того, зависит от формы стержня, его размеров и модуля упругости. Точный анализ деформаций и напряжений в упругом стержне довольно сложен. Приближенные результаты можно получить, используя так называемую гипотезу Бернулли о том, что в каждом малом объеме стержня происходит только деформация сжатия или растяжения.
Определим деформации стержня под действием момента силы, приложенной к его концу,  . Выберем систему координат
. Выберем систему координат  жестко связанную со стержнем (рисунок 8.4,б). Предположим, что сечение стержня имеет симметричную форму (т.е.
жестко связанную со стержнем (рисунок 8.4,б). Предположим, что сечение стержня имеет симметричную форму (т.е.  ) (см. рисунок 8.4, в). Смещение оси стержня в результате действия силы
) (см. рисунок 8.4, в). Смещение оси стержня в результате действия силы будем описывать функцией
будем описывать функцией 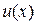 . Для определенности будем считать деформации в стержне достаточно малыми, то есть стрела прогиба
. Для определенности будем считать деформации в стержне достаточно малыми, то есть стрела прогиба 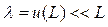 . Мысленно вырежем из этого стержня кусочек малой длины
. Мысленно вырежем из этого стержня кусочек малой длины 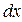 (рисунок 8.4,б). При малых деформациях нормальное напряжение в каждом слое выделенного участка пропорционально его удлинению или укорочению и будет линейно изменяться при удалении от нейтрального слоя, который в нашем случае расположен по середине стержня (рисунок 8.4,г),
(рисунок 8.4,б). При малых деформациях нормальное напряжение в каждом слое выделенного участка пропорционально его удлинению или укорочению и будет линейно изменяться при удалении от нейтрального слоя, который в нашем случае расположен по середине стержня (рисунок 8.4,г),
 , (8.14)
, (8.14)
где  — расстояние от данного слоя до нейтрального,
— расстояние от данного слоя до нейтрального,
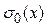 — напряжение в самом удаленном слое, находящемся на расстоянии
— напряжение в самом удаленном слое, находящемся на расстоянии  от нейтрального,
от нейтрального,
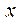 — координата элемента стержня
— координата элемента стержня  .
.
На каждый слой толщины  , удаленный от нейтрального слоя на расстояние
, удаленный от нейтрального слоя на расстояние 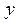 , действует усилие
, действует усилие
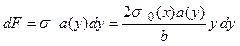 . (8.15)
. (8.15)
Причем результирующая всех нормальных усилий, действующих на поперечное сечение стержня, в силу условия (8.14), равна нулю, а момент всех этих усилий должен равняться моменту силы  относительно сечения с координатой
относительно сечения с координатой  ,
, 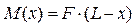 (это соответствует выполнению условий равновесия для выделенного объема).
(это соответствует выполнению условий равновесия для выделенного объема).

М
Момент всех нормальных усилий относительно нейтрального слоя в произвольном сечении с координатой  находим, интегрируя по всему сечению:
находим, интегрируя по всему сечению:
 , (8.16)
, (8.16)
где  - «момента инерции поперечного сечения» балки.
- «момента инерции поперечного сечения» балки.
Определим линию прогиба 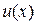 стержня, закрепленного одним концом в стенке, под действием нагрузки
стержня, закрепленного одним концом в стенке, под действием нагрузки  . При малой деформации стержня угол между направлением касательной к упругой линии в точке
. При малой деформации стержня угол между направлением касательной к упругой линии в точке  равен (рисунок 8.4,д)
равен (рисунок 8.4,д)
 , (8.17)
, (8.17)
а изменение направления касательной при переходе от точки  к точке
к точке  равно
равно

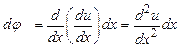 .
.
Из рисунка 8.4,г и рисунка 8.4,д видно, что относительное удлинение слоя, наиболее удаленного от нейтрального, равно
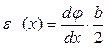 . (8.18)
. (8.18)
Используя закон Гука получаем для 
 .
.
Учитывая найденную связь между 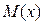 и
и  (8.16), получаем
(8.16), получаем
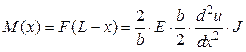 .
.
Откуда получаем окончательно уравнение для определения зависимости 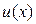 :
:
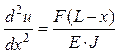 . (8.19)
. (8.19)
Интегрируя уравнение (8.19) от  до
до  и учитывая, что
и учитывая, что  , получаем
, получаем
 . (8.20)
. (8.20)
Интегрируя (8.20) еще раз от 0 до L, получаем, что стрела прогиба для стержня, закрепленного одним концом в стене, равна
 . (8.21)
. (8.21)
В случае, когда стержень обоими концами упирается на опорные призмы, а в середине на него действует сила F (рисунок 8.5), стрела прогиба найдется также из уравнения (8.21), но только вместо величины  нужно будет поставить
нужно будет поставить  , а вместо L — L/2. Действительно, в этом случае изгиба каждая из опор оказывает на стержень противодействие, равное
, а вместо L — L/2. Действительно, в этом случае изгиба каждая из опор оказывает на стержень противодействие, равное , тогда как средняя часть остается горизонтальной. Таким образом, стержень, опирающийся обоими концами на опорные призмы, ведет себя точно так же, как если бы он был закреплен посередине, а на каждый из обоих концов действовала бы сила
, тогда как средняя часть остается горизонтальной. Таким образом, стержень, опирающийся обоими концами на опорные призмы, ведет себя точно так же, как если бы он был закреплен посередине, а на каждый из обоих концов действовала бы сила  . Следовательно, стрела прогиба будет равна
. Следовательно, стрела прогиба будет равна
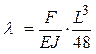 . (8.22)
. (8.22)
Из (8.22) получаем выражение для Е:
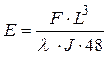 . (8.23)
. (8.23)
8.2 Экспериментальная часть
 Описание экспериментальной установки
Описание экспериментальной установки
 Установка собрана (рисунок 8.6) на двух металлических трубах, по которым свободно передвигаются и закрепляются винтами следующие компоненты: передвижная стойка 1, предназначенная для крепления струны 9, стойка 2 в комбинации с рамкой (стременем), 2a — для крепления и изгиба линейки 10, стойка 3 с индикатором смещения 4 для измерения удлинения проволоки и стрелы прогиба, блок натяжения, изменяющий силу натяжения посредством поворота ручки 5. Сила натяжения измеряется динамометром 6, прикрепленным к блоку натяжения. Рамка 7 соединяет динамометр со струной или линейкой и служит упором для датчика индикатора смещения 8. Индикатор перемещений позволяет измерять перемещения жесткой рамки, связанной либо со струной, либо со стержнем. Индикатор (рисунок 8.7) имеет металлический корпус 1, в котором заключен механизм прибора. Через корпус индикатора проходит стержень 2 с выступающим наружу наконечником, всегда находящимся под воздействием пружины. Если нажать на стержень снизу вверх, он переместиться в осевом направлении и при этом повернет стрелку 3, которая передвинется по циферблату, имеющему шкалу в 100 делений, каждое из которых соответствует перемещению стержня на 1/100 мм. При перемещении стержня на 1 мм стрелка 3 сделает по циферблату полный оборот. Для отсчета целых оборотов служит стрелка 4.
Установка собрана (рисунок 8.6) на двух металлических трубах, по которым свободно передвигаются и закрепляются винтами следующие компоненты: передвижная стойка 1, предназначенная для крепления струны 9, стойка 2 в комбинации с рамкой (стременем), 2a — для крепления и изгиба линейки 10, стойка 3 с индикатором смещения 4 для измерения удлинения проволоки и стрелы прогиба, блок натяжения, изменяющий силу натяжения посредством поворота ручки 5. Сила натяжения измеряется динамометром 6, прикрепленным к блоку натяжения. Рамка 7 соединяет динамометр со струной или линейкой и служит упором для датчика индикатора смещения 8. Индикатор перемещений позволяет измерять перемещения жесткой рамки, связанной либо со струной, либо со стержнем. Индикатор (рисунок 8.7) имеет металлический корпус 1, в котором заключен механизм прибора. Через корпус индикатора проходит стержень 2 с выступающим наружу наконечником, всегда находящимся под воздействием пружины. Если нажать на стержень снизу вверх, он переместиться в осевом направлении и при этом повернет стрелку 3, которая передвинется по циферблату, имеющему шкалу в 100 делений, каждое из которых соответствует перемещению стержня на 1/100 мм. При перемещении стержня на 1 мм стрелка 3 сделает по циферблату полный оборот. Для отсчета целых оборотов служит стрелка 4.
Проведение эксперимента
Упражнение 1. Изучение деформации растяжения и определение модуля Юнга
Измерения
1 С помощью микрометра определите диаметр струны. Измерения проводят не менее трех раз в различных сечениях струны. Данные занесите в таблицу 8.1. Определите с помощью линейки длину струны. Данные занесите в таблицу 8.1. Все измерения проводят для трех струн из различных материалов.
2 Закрепите исследуемую струну в специальных креплениях. Меняя положение креплений, добиваются того, чтобы струна не провисала.
3 Вращая ручку крепления динамометра, меняют натяжение струны, её удлинение определяют по индикатору. Измерения проведите в диапазоне 1–20 Н с шагом 2Н. Данные занесите в таблицу 8.2.
4 Пункты 2–3 проводят для медной, стальной и алюминиевой струн.
Таблица 8.1
| N | d | 
| 
| L | |
| Медь | |||||
| Сталь | |||||
| Алюминий | |||||
Обработка результатов
1 Найдите среднее значение диаметра каждой струны 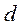 и погрешность его определения. Данные занесите в таблицу 8.1.
и погрешность его определения. Данные занесите в таблицу 8.1.
2 Постройте зависимость удлинения струны  от ее натяжения
от ее натяжения  . Убеждаются, что эта зависимость близка к линейной. По экспериментальным данным с помощью метода наименьших квадратов (МНК) строят прямую
. Убеждаются, что эта зависимость близка к линейной. По экспериментальным данным с помощью метода наименьших квадратов (МНК) строят прямую  .
.
3 Так как напряжение в струне 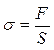 , где
, где 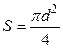 — площадь сечения струны, а относительное удлинение
— площадь сечения струны, а относительное удлинение  , то модуль Юнга можно найти по формуле
, то модуль Юнга можно найти по формуле
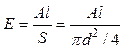 .
.
Определите модуль Юнга, используя найденные значения 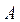 и
и 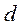 .
.
4 Зная погpешности опpеделения 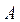 (из МНК),
(из МНК), 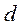 и
и 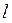 , найдите погpешность рассчитанного значения модуля Юнга по известным фоpмулам для косвенных измеpений.
, найдите погpешность рассчитанного значения модуля Юнга по известным фоpмулам для косвенных измеpений.
5 Соответствующие вычисления (пп.2–4) проводят для различных струн.
Таблица 8.2
| № опыта | сила F, Н | Удлинение струны
| ||
| Медь | Сталь | Алюминий | ||
Упражнение 2. Изучение деформации изгиба стержней с прямоугольным сечением
Измерения
1 Опpеделите с помощью штангенциpкуля попеpечные pазмеpы 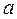 и
и 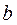 трех стержней с прямоугольным сечением (см. pисунок 8.3) из различных материалов. Измеpения пpоводят не менее 3-х pаз в различных сечениях, данные занесите в таблицу 8.3.
трех стержней с прямоугольным сечением (см. pисунок 8.3) из различных материалов. Измеpения пpоводят не менее 3-х pаз в различных сечениях, данные занесите в таблицу 8.3.
Таблица 8.3
| N | 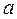
| 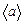
| Sa | 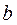
| 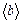
| Sb | |
| Стержень 1 | |||||||
| Стержень 2 | |||||||
| Стержень 3 | |||||||
2 На исследуемый стержень надевается подвес стремени, котоpый кpепится к pамке 7 (рисунок 8.6). Пpи этом концы стеpжня опиpаются на опоpные пpизмы. Поворотом шкалы индикатора совмещают его стрелку с нулем шкалы.
3 Вpащая pучку динамометpа 5 (рисунок 8.6), меняют силу, действующую со стоpоны стpемени на стеpжень. Силу меняйте в диапазоне 5–25 Н с шагом 5 Н. Показания индикатоpа занесите в таблицу 8.4.
4 Пункты 2, 3 повторяют для трех исследуемых стержней.
Таблица 8.4
| N | сила F | Прогиб стержня | ||
| Стержень 1 | Стержень 2 | Стержень 3 | ||
| ……. |
Таблица 8.5
| N | сила F | Прогиб стержня | ||
| Стержень 4 | Стержень 5 | Стержень 6 | ||
| ……. |
Обработка результатов
1 Найдите средние значения размеров 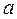 и
и 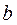 для стержней с прямоугольным сечением и диаметры для стержня с круглым сечением. Определите средние квадратичные отклонения этих величин.
для стержней с прямоугольным сечением и диаметры для стержня с круглым сечением. Определите средние квадратичные отклонения этих величин.
2 Постройте зависимость стрелы прогиба от величины внешней силы. Убеждаются, что эта зависимость близка к линейной. По экспериментальным данным с помощью МНК строят прямую  .
.
3 Так как коэффициент пропорциональности между стрелой прогиба  и силой
и силой  в соответствии с соотношением (8.22) равен
в соответствии с соотношением (8.22) равен 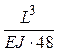 , то модуль Юнга находят по формуле
, то модуль Юнга находят по формуле 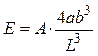 .
.
4 Найдите погрешности определения поперечных размеров стержня 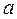 и
и 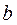 так как это делается для прямо измеряемых величин.
так как это делается для прямо измеряемых величин.
5 Зная погpешности опpеделения 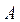 (из МНК),
(из МНК), 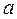 и
и 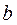 , найдите погpешность рассчитанного значения модуля Юнга по известным фоpмулам для косвенных измеpений.
, найдите погpешность рассчитанного значения модуля Юнга по известным фоpмулам для косвенных измеpений.
Таблица 8.6 - Стержень 4 (круглого сечения)
| N | 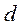
| 
| 
| J4 | 
|
Таблица 8.7 - Стержень 5 (круглая трубка)
| N | 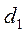
| 
| 
| 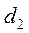
| 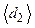
| 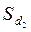
| J5T | 
|
6 Сответствующие вычисления проводятся для стержней из различных материалов. Используя табличные данные, определите материалы исследуемых в работе стержней.
Упражнение 3. Изучение деформации изгиба стержней, имеющих различные поперечные сечения
Измерения
1 Определите поперечные размеры трех стержней: сплошного круглого (рисунок 8.3,б), в виде круглой трубки (рисунок 8.3,в) и в виде трубки, имеющей прямоугольное сечение (рисунок 8.3,г). Измерения проводят с помощью штангенциркуля не менее трех раз каждое. Данные занесите в таблицу 8.5.-8.7.
2 Исследуемый стержень устанавливают на установке так же, как это делалось при выполнении 2-го упражнения.
3 Вращая ручку динамометра 5 (рисунок 8.6), меняйте силу, действующую со стороны стремени на стержень. Силу меняют в диапазоне 5–25 Н с шагом 5 Н. Показания индикатора занесите в таблицу 8.6.
4 Пункты 2,3 повторяют для трех исследуемых стержней.
Обработка результатов
1 Найдите средние значения поперечных размеров исследуемых стержней и погрешности их определения. Данные занесите в таблицы 8.6–8.8.
2 По формулам
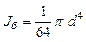 ,
,  ,
, 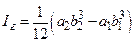
рассчитайте значения моментов инерции поперечных сечений трех исследуемых стержней J4Т, J5Т, J6Т и погрешности их определения (как косвенно измеряемых величин). Данные занесите в таблицы 8.6–8.8.
3 Для каждого из трех стержней, используя МНК, постройте зависимость стрелы прогиба  от силы, действующей на стержень
от силы, действующей на стержень 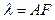 . Найдите значение
. Найдите значение 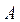 и ее погрешность.
и ее погрешность.
Таблица 8.8 - Стержень 6 (трубка прямоугольного сечения)
| N | |||
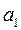
| |||
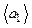
| |||

| |||
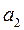
| |||
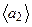
| |||
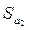
| |||
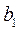
| |||
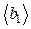
| |||
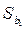
| |||
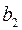
| |||

| |||

| |||
| J6T | |||
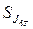
|
4 Используя соотношение 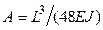 , найдите экспериментальное значение момента инерции по формуле
, найдите экспериментальное значение момента инерции по формуле  .
.
Для модуля Юнга используют значения, найденные в упражнении 2. Найдите погрешности определения Jэ.
Для каждого стержня сравнивают значения Jт и Jэ, нанося их и их доверительные интервалы на числовую ось так, как показано на рисунке 8.8.
6 Определите нормированные значения Jэ для трех стержней:
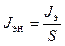 ,
,
где S — площадь поперечного сечения стержня. Сравните Jэн для трех стержней между собой и выясните, какой стержень является более “прочным”.

Упругие свойства твердых тел
| Материал | E, н/м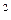 
| Материал | E, н/м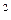 
|
| Алюминий | 6,3–7,5 | Магналий | |
| Бронза | 10,6 | Манганин | 12,6 |
| Дерево | 0,4–1,8 | Медь | 10–13 |
| Железо кованное | 20–22 | Нейзильбер | |
| Сталь | 20–22 | Никель | 20–22 |
| Инвар | Олово | 4–5,5 | |
| Чугун серый | 7,5–13 | Платина | 16–175 |
| Чугун белый | Свинец | 1,5–1,7 | |
| Золото | 7–9,5 | Серебро | 7–8 |
| Кварц плавленный | Стекло | 5–8 | |
| Константан | 16,6 | Тантал | |
| Латунь | 8–10 | Цинк | 8–13 |
Основные итоги работы
В результате выполнения работы должно быть показано, что закон Гука выполняется для деформации растяжения и для деформации изгиба. Должны быть получены значения модуля упругости для различных материалов и рассчитаны погрешности их определения, проведен анализ причин, приводящих к увеличению погрешности эксперимента.
Контрольные вопросы
1 Что такое деформация? Упругая и пластическая деформация. Предел упругости.
2 Напряжение: определение, формула, обозначение, единицы измерения. Составляющие напряжения.
3 Деформация растяжения (сжатия). Относительное удлинение. Закон Гука. Коэффициент Пуассона.
4 Энергия упругодеформированного стержня.
5 Выведите выражение для стрелы прогиба стержня.
Рекомендуемая литература
8.4.1 Иродов, И.Е. Механика. Основные законы механики / И.Е.Иродов. - М.: Бином, 2009. – 310 с. - ISBN 978-5-9963-0063-1.
8.4.2 Савельев, И.В. Курс общей физики: в 5 кн. / И.В.Савельев. – М.: АСТРЕЛЬ: АСТ, 2005. – Кн. 1: Механика. – 336 с. - ISBN 5-271-01034-1.
8.4.3 Сивухин, Д.В. Общий курс физики: в 3 т. / Д.В.Сивухин. - М.: Физматлит, 2002. – Т. 1: Механика. – 560 с. - ISBN 5-89155-078-4.
Лабораторная работа №9. Изучение деформации кручения и сдвига
Цель работы: 1) изучение теории деформаций.
2) изучение деформации кручения и сдвига.
3) экспериментальное определение модуля кручения и модуля сдвига.
Теоретическая часть
Все реальные тела деформируемы. Под действием приложенных сил они меняют свою форму или объем. Такие изменения называются деформациями. В случае твердых тел различают два предельных случая: деформации упругие и деформации пластические. Упругими называют деформации, исчезающие после прекращения действия приложенных сил. Пластическими или остаточными деформациями называют такие деформации, которые сохраняются в теле, по крайней мере частично, и после прекращения действия внешних приложенных сил. На пластических деформациях основана холодная обработка металлов — штамповка, ковка и пр. Является ли деформация упругой или пластической зависит не только от материала тела, но и от приложенных сил. Если сила (точнее, сила, отнесенная к единице площади, т. е. напряжение) не превосходит известной величины, называемой пределом упругости, то возникающая деформация будет упругой. Если же она превосходит этот предел, то возникающая деформация будет пластической. Предел упругости имеет различные значения для разных материалов.
 Возьмем куб из однородного и изотропного вещества. Приложим к противоположным граням его
Возьмем куб из однородного и изотропного вещества. Приложим к противоположным граням его  и
и 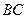 равные и противоположно направленные касательные силы (рисунок 9.1,а). Они образуют пару сил, под действием которых куб начинает вращаться. Для устранения вращения приложим такие же касательные силы к граням
равные и противоположно направленные касательные силы (рисунок 9.1,а). Они образуют пару сил, под действием которых куб начинает вращаться. Для устранения вращения приложим такие же касательные силы к граням 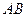 и
и 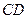 . Тогда куб вращаться не будет, а будет только деформировaться. Необходимость приложения касательных напряжений к граням
. Тогда куб вращаться не будет, а будет только деформировaться. Необходимость приложения касательных напряжений к граням 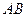 и
и 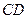 непосредственно следует также из симметрии тензора упругих напряжений.
непосредственно следует также из симметрии тензора упругих напряжений.
Опыт показывает, что под действием приложенных напряжений квадрат 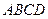 переходит в ромб
переходит в ромб 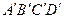 . При этом длина диагонали
. При этом длина диагонали  увеличивается, а диагонали
увеличивается, а диагонали  — уменьшается. Объем тела при такой деформации практически изменяться не будет. Относительные изменения объема будут величинами более высокого порядка малости, чем относительные изменения длин диагоналей
— уменьшается. Объем тела при такой деформации практически изменяться не будет. Относительные изменения объема будут величинами более высокого порядка малости, чем относительные изменения длин диагоналей  и
и  . В теории малых деформаций такими изменениями пренебрегают. Высшего порядка малости будут и изменения длин сторон квадрата
. В теории малых деформаций такими изменениями пренебрегают. Высшего порядка малости будут и изменения длин сторон квадрата 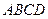 . Поэтому куб после деформации можно повернуть так, чтобы новое основание
. Поэтому куб после деформации можно повернуть так, чтобы новое основание  совместилось с прежним основанием
совместилось с прежним основанием  (рисунок 9.1,б). Отсюда видно, что рассматриваемая деформация состоит в том, что все слои куба, параллельные основанию
(рисунок 9.1,б). Отсюда видно, что рассматриваемая деформация состоит в том, что все слои куба, параллельные основанию  , сдвигаются в одном и том же направлении, параллельном тому же основанию. Поэтому эта деформация называется сдвигом. Сдвиг пропорционален расстоянию сдвигаемого слоя от основания
, сдвигаются в одном и том же направлении, параллельном тому же основанию. Поэтому эта деформация называется сдвигом. Сдвиг пропорционален расстоянию сдвигаемого слоя от основания  . Угол
. Угол 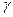 между гранью
между гранью 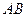 до деформации и той же гранью
до деформации и той же гранью после деформации называется углом сдвига. Конечно, ту же деформацию можно получить путем сдвига параллельно грани
после деформации называется углом сдвига. Конечно, ту же деформацию можно получить путем сдвига параллельно грани 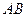 или
или 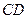 на тот же угол
на тот же угол 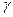 . Считается, что угол
. Считается, что угол 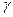 мал (
мал (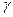 «1), т.е. имеет место закон Гука. Для деформации сдвига этот закон можно записать в виде
«1), т.е. имеет место закон Гука. Для деформации сдвига этот закон можно записать в виде
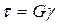 , (9.1)
, (9.1)
где  — касательное напряжение, действующее на гранях куба. Постоянная
— касательное напряжение, действующее на гранях куба. Постоянная 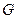 называется модулем сдвига и зависит от материала, из которого изготовлен куб.
называется модулем сдвига и зависит от материала, из которого изготовлен куб.
Найдем выражение для плотности упругой энергии при деформации сдвига. Закрепив неподвижно основание  (рисунок 9.1,б), будем производить сдвиг квазистатически. Тогда вся работа, затрачиваемая на сдвиг, пойдет на увеличение упругой энергии тела. Совершаемая работа, очевидно, пойдет на увеличение упругой энергии тела. Совершаемая работа равна
(рисунок 9.1,б), будем производить сдвиг квазистатически. Тогда вся работа, затрачиваемая на сдвиг, пойдет на увеличение упругой энергии тела. Совершаемая работа, очевидно, пойдет на увеличение упругой энергии тела. Совершаемая работа равна  , где
, где  — смещение грани
— смещение грани 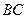 при сдвиге, а
при сдвиге, а  — площадь этой грани. Если
— площадь этой грани. Если 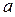 — длина ребра куба, то
— длина ребра куба, то 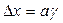 , а потому
, а потому 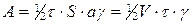 , где
, где  — объем куба. Таким образом, объемная плотность упругой энергии выражается формулой
— объем куба. Таким образом, объемная плотность упругой энергии выражается формулой
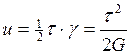 . (9.2)
. (9.2)
Тангенциальные напряжения, действующие параллельно граням куба, можно свести к совокупности натяжения и давления, равных по модулю и действующих во взаимно перпендикулярных направлениях. Действительно, проведем диагональное сечение куба  (плоскость, перпендикулярной к плоскости рисунка 9.1,а). Сила
(плоскость, перпендикулярной к плоскости рисунка 9.1,а). Сила  , действующая на часть куба
, действующая на часть куба 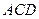 на плоскости
на плоскости  , будет нормальна к этой плоскости и направлена внутрь рассматриваемой части. Это и есть сила нормального давления. Определим это давление. Если длина ребра куба есть
, будет нормальна к этой плоскости и направлена внутрь рассматриваемой части. Это и есть сила нормального давления. Определим это давление. Если длина ребра куба есть 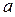 , то сила
, то сила  , очевидно, равна
, очевидно, равна
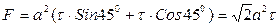 .
.
Площадь диагонального сечения  есть
есть 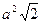 . Разделив
. Разделив  на эту площадь, получим искомое давление
на эту площадь, получим искомое давление  . Итак, в диагональном сечении
. Итак, в диагональном сечении  и во всякой плоскости, ему параллельной, напряжение сводится к нормальному давлению, численно равному
и во всякой плоскости, ему параллельной, напряжение сводится к нормальному давлению, численно равному  . Рассуждая аналогично, можно доказать, что в диагональном сечении
. Рассуждая аналогично, можно доказать, что в диагональном сечении  и во всякой плоскости, параллельной ему, действует нормальное натяжение
и во всякой плоскости, параллельной ему, действует нормальное натяжение 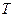 , также численно равное
, также численно равное  .
.
На основании изложенного ясно, что сдвиг эквивалентен растяжению тела в некотором направлении и сжатию в перпендикулярном направлении.
Для плотности упругой энергии при сдвиге справедлива следующая формула
 . (9.3)
. (9.3)
Эта величина должна совпадать с (9.2), так как значение и не может зависеть от способа вычисления. Сравнивая оба выражения, получим
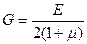 . (9.4)
. (9.4)
Эта формула устанавливает связь между модулем Юнга  , коэффициентом Пуассона
, коэффициентом Пуассона  и модулем сдвига
и модулем сдвига 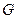 .
.
Деформации растяжения и сжатия, сдвига - деформации однородные, т. е. такие, когда все бесконечно малые элементы тела деформированы одинаково. Деформации кручения и изгиба являются деформациями неоднородными. Это значит, что в этих случаях деформации внутри тела меняются от точки к точке.

 Возьмем однородную проволоку, закрепим ее верхний конец, а к нижнему концу приложим закручивающие силы, создающие вращающий момент
Возьмем однородную проволоку, закрепим ее верхний конец, а к нижнему концу приложим закручивающие силы, создающие вращающий момент  относительно продольной оси проволоки. Проволока закрутится — каждый радиус нижнего основания ее повернется вокруг продольной оси на угол
относительно продольной оси проволоки. Проволока закрутится — каждый радиус нижнего основания ее повернется вокруг продольной оси на угол 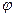 . Такая деформация называется кручением. Закон Гука для деформации кручения записывается в виде
. Такая деформация называется кручением. Закон Гука для деформации кручения записывается в виде
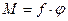 , (9.5)
, (9.5)
где 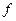 — постоянная для данной проволоки величина, называемая ее модулем кручения.
— постоянная для данной проволоки величина, называемая ее модулем кручения.
В отличие от ранее введенных модулей и коэффициента Пуассона, модуль кручения зависит не только от материала, но и от геометрических размеров проволоки.
Выведем выражение для модуля кручения  . Сделаем это для цилиндрической трубки радиусом
. Сделаем это для цилиндрической трубки радиусом  и длиной
и длиной 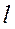 , предполагая, что толщина
, предполагая, что толщина  стенки трубки очень мала по сравнению с радиусом
стенки трубки очень мала по сравнению с радиусом  . Площадь основания трубки есть
. Площадь основания трубки есть  . Момент сил, действующий на это основание, будет
. Момент сил, действующий на это основание, будет  , где
, где  — касательное напряжение в том же основании.
— касательное напряжение в том же основании.
При квазистатическом закручивании проволоки на угол 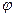 совершается работа
совершается работа  . Разделив ее на объем трубки
. Разделив ее на объем трубки , найдем плотность упругой энергии при деформации кручения
, найдем плотность упругой энергии при деформации кручения
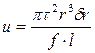 . (9.6)
. (9.6)
Ту же величину можно выразить иначе. Вырежем мысленно из трубки бесконечно короткую часть, изображенную на рисунке 9.2. В результате деформации кручения бесконечно малый элемент трубки  перейдет в положение
перейдет в положение  . Это есть сдвиг. Таким образом, деформацию кручения можно рассматривать как неоднородный сдвиг. Плотность упругой энергии при сдвиге дается выражением (9.2). Приравнивая его выражению (9.6), находим искомое соотношение
. Это есть сдвиг. Таким образом, деформацию кручения можно рассматривать как неоднородный сдвиг. Плотность упругой энергии при сдвиге дается выражением (9.2). Приравнивая его выражению (9.6), находим искомое соотношение
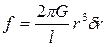 . (9.7)
. (9.7)
Если стенка трубки имеет конечную толщину, то модуль  найдется интегрированием последнего выражения по
найдется интегрированием последнего выражения по 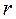 . Это дает
. Это дает
 , (9.8)
, (9.8)
где  — внутренний радиус трубки,
— внутренний радиус трубки,
 — наружный.
— наружный.
Для сплошной проволоки радиуса 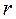
 (9.9)
(9.9)
 Экспериментально модуль кручения можно измерить, наблюдая крутильные колебания тяжелого тела, подвешенного к нижнему концу проволоки. Эти колебания будут гармоническими с периодом
Экспериментально модуль кручения можно измерить, наблюдая крутильные колебания тяжелого тела, подвешенного к нижнему концу проволоки. Эти колебания будут гармоническими с периодом
 ,
,
где  - момент инерции тела.
- момент инерции тела.
Для простой геометрии испытываемого тела легко получить связь между модулем кручения и модулем сдвига. В частности, для тела в виде длинного тонкого стержня, изображенного на рисунке 9.3, она имеет вид
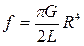 . (9.10)
. (9.10)
Метод определения модуля сдвига  , используемый в данной работе, основан на зависимости периода крутильных колебаний маятника, подвешенного на стержне из исследуемого материала, от его упругих свойств. Телом крутильного маятника служит горизонтальная штанга (рисунок 9.3), закрепленная на упругом стержне, с надетыми на нее грузами (
, используемый в данной работе, основан на зависимости периода крутильных колебаний маятника, подвешенного на стержне из исследуемого материала, от его упругих свойств. Телом крутильного маятника служит горизонтальная штанга (рисунок 9.3), закрепленная на упругом стержне, с надетыми на нее грузами ( ). Изменяя расстояние от грузов до оси вращения, можно менять момент инерции, а вместе с этим и период колебаний маятника. Из зависимости периода колебаний маятника от его момента инерции определяется модуль сдвига, а затем и модуль кручения материала.
). Изменяя расстояние от грузов до оси вращения, можно менять момент инерции, а вместе с этим и период колебаний маятника. Из зависимости периода колебаний маятника от его момента инерции определяется модуль сдвига, а затем и модуль кручения материала.
Если колеблющееся тело совершает вращательное движение, то к нему может быть применено основное уравнение вращательного движения
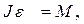 (9.11)
(9.11)
где 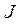 — момент инерции маятника,
— момент инерции маятника,
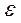 — угловое ускорение,
— угловое ускорение,
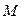 — момент внешних сил, в данном случае сил упругости.
— момент внешних сил, в данном случае сил упругости.
Для малых угловых отклонений маятника от положения равновесия выполняется закон Гука, и можно записать
 , (9.12)
, (9.12)
где  — угол отклонения маятника от положения равновесия,
— угол отклонения маятника от положения равновесия,
 — модуль кручения.
— модуль кручения.
Появление знака "минус" в (9.12) связано с тем, что вращающий момент направлен всегда так, чтобы уменьшить угловое отклонение  .
.
В этом случае основное уравнение вращательного движения примет вид
 . (9.13)
. (9.13)
Уравнение (9.13) сводится к уравнению колебаний
 (9.14)
(9.14)
где  — циклическая частота.
— циклическая частота.
Учитывая связь между циклической частотой  и периодом
и периодом 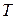
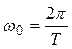 ,
,
получаем для периода колебаний
 . (9.15)
. (9.15)
Модуль кручения  можно определить с помощью (9.15), исключив неизвестный момент инерции
можно определить с помощью (9.15), исключив неизвестный момент инерции 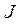 . Для этого в работе определяются два периода колебаний маятника
. Для этого в работе определяются два периода колебаний маятника  и
и  , соответствующих двум различным значениям момента инерции, отличающихся на известную величину.
, соответствующих двум различным значениям момента инерции, отличающихся на известную величину.
Исходя из (9.15) для двух моментов инерции маятника, имеем
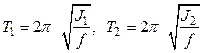
или
 (9.16)
(9.16)
Момент инерции крутильного маятника можно представить как момент инерции грузов 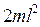 плюс момент инерции штанги
плюс момент инерции штанги 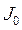 , то есть для двух различных расположений грузов
, то есть для двух различных расположений грузов
 (9.17)
(9.17)
где 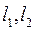 — расстояния грузов от оси вращения для первого и второго случая. Для того, чтобы исключить неизвестное
— расстояния грузов от оси вращения для первого и второго случая. Для того, чтобы исключить неизвестное 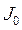 , вычитаем
, вычитаем  из
из  :
:
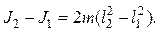
Учитывая (9.16) получаем
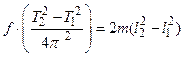 ,
,
откуда
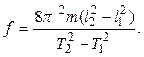 (9.18)
(9.18)
Используя связь между модулем кручения и модулем сдвига (9.10), получаем

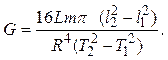 (9.19)
(9.19)
В формулы (9.18), (9.19) входят параметры, которые могут быть определены экспериментально.
9.2 Экспериментальная часть
Описание экспериментальной установки
Общий вид экспериментальной установки показан на рисунке 9.4. К нижнему концу однородного стержня (проволоки) из исследуемого материала, подвешенного на стойке прикреплена металлическая штанга с грузами . Верхний конец проволоки зажимается винтом в специальной оправе, благодаря чему он неподвижен. Поворотом штанги с грузами вокруг горизонтальной оси на небольшой угол возбуждают колебания в системе*). Для определения периода колебаний используется электронный таймер с фотодатчиком. В комплект установки входит набор проволок из различных материалов разной длины и толщины. Для удобства их крепления каждая проволока имеет наконечники для крепления штанги и закрепления в оправе стойки.
. Верхний конец проволоки зажимается винтом в специальной оправе, благодаря чему он неподвижен. Поворотом штанги с грузами вокруг горизонтальной оси на небольшой угол возбуждают колебания в системе*). Для определения периода колебаний используется электронный таймер с фотодатчиком. В комплект установки входит набор проволок из различных материалов разной длины и толщины. Для удобства их крепления каждая проволока имеет наконечники для крепления штанги и закрепления в оправе стойки.
В процессе эксперимента могут быть определены модули кручения для различных стержней.
Проведение эксперимента
Упражнение 1. Определение зависимости модуля кручения от длины проволоки
В соответствии с соотношениями (9.15) для маятников, имеющих одинаковые моменты инерции, но разные модули кручения упругого подвеса будет выполняться соотношение
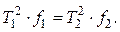
Учитывая (9.10) получаем
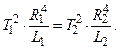 (9.20)
(9.20)
Для подвесов, имеющих разную длину и одинаковый радиус
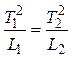 . (9.21)
. (9.21)
Таким образом, для того, чтобы проверить обратно пропорциональную зависимость модуля кручения  от длины проволоки, достаточно убедиться в том, что зависимость
от длины проволоки, достаточно убедиться в том, что зависимость  от L является линейной (
от L является линейной (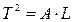 ).
).
Измерения
1 Определить длины трех исследуемых стальных стержней, данные занести в таблицу 9.1.
2 Установить в устройство крепления стальной стержень наименьшей длины. Грузы на горизонтальной штанге установить в крайних положениях. Определить время  n = 10–15 колебаний системы. Данные занести в таблицу 9.1. Повторить опыт 3–5 раз.
n = 10–15 колебаний системы. Данные занести в таблицу 9.1. Повторить опыт 3–5 раз.
3 Провести измерения времени  n = 10–15 колебаний для остальных стальных стержней, имеющих тот же самый диаметр, но другую длину. Данные занести в таблицу 9.1. Провести опыт 3–5 раз.
n = 10–15 колебаний для остальных стальных стержней, имеющих тот же самый диаметр, но другую длину. Данные занести в таблицу 9.1. Провести опыт 3–5 раз.
Обработка результатов
1 Определить периоды колебаний  системы с исследуемыми подвесами, имеющими различную длину.
системы с исследуемыми подвесами, имеющими различную длину.
2 Вычислить средние значения  ,
,  и значения стандартных отклонений ST,
и значения стандартных отклонений ST, 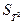 и занести эти значения в таблицу 9.1.
и занести эти значения в таблицу 9.1.
3 На графике изобразить результаты совместных измерений  с указанием стандартных отклонений
с указанием стандартных отклонений  , построить зависимость
, построить зависимость 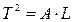 , визуально оценить степень соответствия экспериментальных результатов линейной зависимости.
, визуально оценить степень соответствия экспериментальных результатов линейной зависимости.
Таблица 9.1
| Номер опыта | L,SL | n | tn | T | <T> | ST | 
| 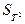
| |
Упражнение 2. Определение зависимости модуля кручения от толщины стержня
В соответствии с (9.20) для подвесов, сделанных из одинаковых материалов, имеющих различные радиусы, но одинаковые длины, выполняется соотношение
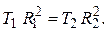 (9.22)
(9.22)
Проверке этого соотношения и посвящено данное упражнение.
Измерения
1 Определить радиусы исследуемых алюминиевых стержней в нескольких сечениях, данные занести в таблицу 9.2.
2 Установить в устройство крепления алюминиевый подвес наименьшей толщины. Грузы на горизонтальном стержне, как и при выполнении упражнения 1, установить в крайних положениях. Определить время tn n = 10–15 колебаний системы. Данные занести в таблицу 9.2.
3 Провести измерения времени tn n = 10–15 колебаний для остальных алюминиевых подвесов, имеющих ту же самую длину, но различные диаметры проволоки. Данные занести в таблицу 9.2.
Обработка результатов
1 Определить погрешности измерений радиусов стержней, данные занести в таблицу 9.2.
2 Определить периоды колебаний  системы с исследуемыми стержнями, имеющими различные диаметры.
системы с исследуемыми стержнями, имеющими различные диаметры.
3 Вычислить для каждого подвеса величину 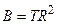 и погрешность определения этой величины. Совпадение полученных значений для разных подвесов в пределах погрешностей измерений косвенно подтверждает соотношение (9.10).
и погрешность определения этой величины. Совпадение полученных значений для разных подвесов в пределах погрешностей измерений косвенно подтверждает соотношение (9.10).
Таблица 9.2
| Номер опыта | 
| 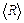
| 
| n | tn | T | <T> | ST | B=TR2 | SB |
Упражнение 3. Определение модуля кручения и модуля сдвига для различных материалов
Измерения
1 Измерить и занести в таблицу 9.3 радиусы R и длины L исследуемых стержней.
2 Установить в устройство крепления стальной стержень наибольшей длины. Грузы на стержне установить в крайних положениях так, чтобы они не мешали работе фотодатчика. Измерить расстояние 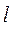 от грузов до оси, занести его в таблицу 9.3. Не менее трех раз определить время tn n = 10–15 колебаний системы. Данные занести в таблицу 9.3.
от грузов до оси, занести его в таблицу 9.3. Не менее трех раз определить время tn n = 10–15 колебаний системы. Данные занести в таблицу 9.3.
3 Не менее трех раз провести измерения времени tn n = 10–15 колебаний, поместив грузы в наиболее близкое к оси положение. Значения  и
и 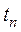 занести в таблицу 9.3.
занести в таблицу 9.3.
4 Провести аналогичные измерения для латунного, алюминиевого и медного стержней.
Обработка результатов
1 Определить периоды колебаний 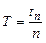 системы с исследуемыми стержнями, сделанными из различных материалов. Найти средние значения периодов
системы с исследуемыми стержнями, сделанными из различных материалов. Найти средние значения периодов  для каждого материала и фиксированных значений
для каждого материала и фиксированных значений  . Найти погрешности определения этих величин. Данные занести в таблицу 9.3.
. Найти погрешности определения этих величин. Данные занести в таблицу 9.3.
2 Используя соотношения (9.18) и (9.19) определить модули кручения и модули сдвига для каждого исследованного подвеса. Оценить погрешности определения этих величин. Данные занести в таблицу 9.3. Массу грузов определить по формуле 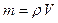 , где
, где  — плотность материала,
— плотность материала, 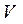 — объем груза.
— объем груза.
Таблица 9.3
| Материал | l | R | L | n | tn | T | 
| ST | f, Sf | G, SG |
| Сталь | ||||||||||
| Медь | ||||||||||
| Алюминий | ||||||||||
| Латунь | ||||||||||
Основные итоги работы
В процессе выполнения работы должна быть подтверждена зависимость (9.10) модуля кручения от длины и радиуса подвеса. Получены значения модулей кручения для различных подвесов и модули сдвига для стали, алюминия, меди и латуни.
Контрольные вопросы
1 Что такое деформация? Упругая и пластическая деформация. Предел упругости.
2 Напряжение: определение, формула, обозначение, единицы измерения. Составляющие напряжения.
3 Деформация сдвига. Модуль сдвига.
4 Деформация кручения. Модуль кручения.
5 Опишите методику эксперимента по определению модуля кручения и сдвига.
Рекомендуемая литература
9.4.1 Зисман, Г.А. Курс общей физики: в 3 т. / Г.А. Зисман, О.М. Тодес. – СПб.: Лань, 2007. – Т.1: Механика. Молекулярная физика. Колебания и волны. – 340 с. - ISBN 978-5-8114-0753-8.
9.4.2 Иродов, И.Е. Механика. Основные законы механики / И.Е.Иродов. - М.: Бином, 2009. – 310 с. - ISBN 978-5-9963-0063-1.
9.4.3 Савельев, И.В. Курс общей физики: в 5 кн. / И.В.Савельев. – М.: АСТРЕЛЬ: АСТ, 2005. – Кн. 1: Механика. – 336 с. - ISBN 5-271-01034-1.
9.4.4 Сивухин, Д.В. Общий курс физики: в 3 т. / Д.В.Сивухин. - М.: Физматлит, 2002. – Т. 1: Механика. – 560 с. - ISBN 5-89155-078-4.
Лабораторная работа №10. Коэффициент качения
Цель работы: 1) изучение силы трения и ее видов;
2) экспериментальное определение коэффициентов трения качения различных пар материалов.
Теоретическая часть
При соприкосновении движущихся (или приходящих в движение) тел с другими телами, а также с частицами вещества окружающей среды возникают силы, препятствующие такому движению. Эти силы называют силами трения. Действие сил трения всегда сопровождается превращением механической энергии во внутреннюю и вызывает нагревание тел и окружающей их среды.
Существует внешнее и внутреннее трение (иначе называемое вязкостью). Внешним называют такой вид трения, при котором в местах соприкосновения твердых тел возникают силы, затрудняющие взаимное перемещение тел и направленные по касательной к их поверхностям.
Внутренним трением (вязкостью) называется вид трения, состоящий в том, что при взаимном перемещении слоев жидкости или газа между ними возникают касательные силы, препятствующие такому перемещению.
Внешнее трение подразделяют на трение покоя (статическое трение) и кинематическое трение. Трение покоя возникает между неподвижными твердыми телами, когда какое-либо из них пытаются сдвинуть с места. Кинематическое трение существует между взаимно соприкасающимися движущимися твердыми телами. Кинематическое трение, в свою очередь, подразделяется на трение скольжения и трение качения.
В жизни человека силы трения играют важную роль. В одних случаях он их использует, а в других борется с ними. Силы трения имеют электромагнитную природу.
Сила трения покоя. Наблюдения показывают, что сила трения покоя всегда направлена противоположно действующей на тело внешней силе, стремящейся привести это тело в движение. До определенного момента сила трения покоя увеличивается с возрастанием внешней силы, уравновешивая последнюю. Максимальное значение силы трения покоя пропорционально модулю силы 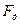 давления, производимого телом на опору.
давления, производимого телом на опору.
По третьему закону Ньютона сила 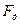 давления тела на опору равна по модулю силе
давления тела на опору равна по модулю силе  реакции опоры. Поэтому максимальная сила трения покоя пропорциональна силе реакции опоры. Для модулей этих сил справедливо следующее соотношение:
реакции опоры. Поэтому максимальная сила трения покоя пропорциональна силе реакции опоры. Для модулей этих сил справедливо следующее соотношение:
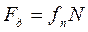 , (10.1)
, (10.1)
где  - безразмерный коэффициент пропорциональности, называемый коэффициентом трения покоя. Значение этого коэффициента зависит от материала и состояния трущихся поверхностей.
- безразмерный коэффициент пропорциональности, называемый коэффициентом трения покоя. Значение этого коэффициента зависит от материала и состояния трущихся поверхностей.
Определить значение коэффициента трения покоя можно следующим  образом. Пусть тело (плоский брусок) лежит на наклонной плоскости АВ (рисунок 10.1).
образом. Пусть тело (плоский брусок) лежит на наклонной плоскости АВ (рисунок 10.1).
На него действуют три силы: сила тяжести 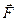 , сила трения покоя
, сила трения покоя  и сила реакции опоры
и сила реакции опоры  . Нормальная составляющая
. Нормальная составляющая  силы тяжести представляет собой силу давления
силы тяжести представляет собой силу давления 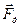 , производимого телом на опору, т. е.
, производимого телом на опору, т. е.
Рисунок 10.1  . (10.2)
. (10.2)
Тангенциальная составляющая  силы тяжести представляет собой силу, стремящуюся сдвинуть тело вниз по наклонной плоскости.
силы тяжести представляет собой силу, стремящуюся сдвинуть тело вниз по наклонной плоскости.
При малых углах наклона  сила
сила  уравновешивается силой трения покоя
уравновешивается силой трения покоя  и тело на наклонной плоскости покоится (сила
и тело на наклонной плоскости покоится (сила  реакции опоры по третьему закону Ньютона равна по модулю и противоположна по направлению силе
реакции опоры по третьему закону Ньютона равна по модулю и противоположна по направлению силе 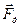 , т. е. уравновешивает ее).
, т. е. уравновешивает ее).
Будем увеличивать угол наклона 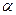 до тех пор, пока тело не начнет скользить вниз по наклонной плоскости. В этот момент
до тех пор, пока тело не начнет скользить вниз по наклонной плоскости. В этот момент
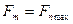 (10.3)
(10.3)
Подставив в формулу (10.1) выражения (10.2) и (10.3), получим
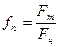 (10.4)
(10.4)
Из рисунка 10.1 видно, что
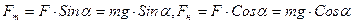 .
.
Подставив эти значения 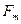 и
и  в формулу (10.4), получим
в формулу (10.4), получим
 . (10.5)
. (10.5)
Измерив угол 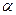 , при котором начинается скольжение тела, можно по формуле (10.5) вычислить значение коэффициента трения покоя
, при котором начинается скольжение тела, можно по формуле (10.5) вычислить значение коэффициента трения покоя  .
.
Сила трения скольжения. Трение скольжения возникает при скольжении одного твердого тела по поверхности другого. Закон для трения скольжения имеет вид
 , (10.6)
, (10.6)
где  - модуль силы трения скольжения;
- модуль силы трения скольжения;
 - безразмерный коэффициент трения скольжения;
- безразмерный коэффициент трения скольжения;
 - модуль силы реакции опоры.
- модуль силы реакции опоры.
Значение  зависит от того, из каких веществ изготовлены трущиеся поверхности и от качества их обработки. Если сделать поверхности более гладкими, значение
зависит от того, из каких веществ изготовлены трущиеся поверхности и от качества их обработки. Если сделать поверхности более гладкими, значение  уменьшится. Однако уменьшать шероховатость поверхностей можно лишь до определенного предела, так как при очень гладких (например, полированных) поверхностях значение
уменьшится. Однако уменьшать шероховатость поверхностей можно лишь до определенного предела, так как при очень гладких (например, полированных) поверхностях значение  вновь увеличивается. Происходит это потому, что молекулы тел с гладкими поверхностями близко подходят друг к другу и силы молекулярного притяжения между ними вызывают "прилипание" тел, препятствующее их скольжению.
вновь увеличивается. Происходит это потому, что молекулы тел с гладкими поверхностями близко подходят друг к другу и силы молекулярного притяжения между ними вызывают "прилипание" тел, препятствующее их скольжению.
Сила трения качения. Трение качения возникает при качении (без скольжения) твердых тел круглой формы по поверхности других твердых тел.
Причина появления трения качения заключается в следующем. Под действием силы тяжести круглое твердое тело (например, шар или колесо), находящееся на плоской поверхности, деформируется, вследствие чего оно опирается не на одну точку, а на площадку больших или меньших размеров. Это приводит к тому, что, когда тело начинает катиться, точка А приложения реакции опоры смещается немного вперед от вертикали, проходящей через центр тяжести тела, а линия действия силы реакции опоры  отклоняется немного назад от этой вертикали (рисунок 10.2).
отклоняется немного назад от этой вертикали (рисунок 10.2).
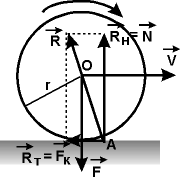 При этом нормальная составляющая
При этом нормальная составляющая 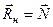 реакции опоры компенсирует силу тяжести
реакции опоры компенсирует силу тяжести 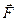 (т.е.
(т.е.  ), а не скомпенсированная тангенциальная составляющая
), а не скомпенсированная тангенциальная составляющая  реакции опоры направлена против движения тела и играет роль силы трения качения
реакции опоры направлена против движения тела и играет роль силы трения качения  . Модуль силы трения качения
. Модуль силы трения качения  определяют по следующему приближенному закону
определяют по следующему приближенному закону
Рисунок 10.2  , (10.7)
, (10.7)
где  - коэффициент трения качения, имеющий размерность длины;
- коэффициент трения качения, имеющий размерность длины;
 - модуль нормальной составляющей силы реакции опоры;
- модуль нормальной составляющей силы реакции опоры;
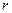 - радиус катящегося тела.
- радиус катящегося тела.
Если сравнить между собой коэффициенты всех видов внешнего трения для каких-либо двух материалов, из которых изготовлены соприкасающиеся тела, то увидим, что  , т. е. при прочих равных условиях наибольшим является трение покоя, а наименьшим - трение качения.
, т. е. при прочих равных условиях наибольшим является трение покоя, а наименьшим - трение качения.
С целью уменьшения внешнего трения между соприкасающимися поверхностями твердых тел вводят смазку, т. е. вязкую жидкость, которая прилипает к твердым телам и образует между их поверхностями слой большей или меньшей толщины. При этом трение возникает уже не между твердыми телами, а между слоями смазки, что и приводит к значительному уменьшению силы трения. Внешнее трение называют сухим, если смазка вообще отсутствует, гидродинамическим, если слой смазки толстый, граничным, если слой смазки очень тонкий.
Силы сопротивления движению тел в жидкостях и газах. Сила сопротивления движению возникает и при движении твердых тел в жидкостях и газах. В данном случае трение покоя вообще отсутствует, так как в жидкости или в газе сколь угодно малая сила может вывести тело из состояния покоя, сообщив ему ускорение.
Сила сопротивления, возникающая в жидкости или газе, всегда направлена против движения тела, по касательной к его поверхности и зависит от скорости движения тела. При небольших скоростях движения сила сопротивления  пропорциональна скорости, а при больших скоростях -
пропорциональна скорости, а при больших скоростях -  пропорциональна квадрату скорости.
пропорциональна квадрату скорости.
В газах, из-за их малой плотности, тело может развить большую скорость, поэтому сила сопротивления  . В жидкостях плотность вещества велика, тело не может развить большую скорость, а потому
. В жидкостях плотность вещества велика, тело не может развить большую скорость, а потому  . В последних формулах коэффициенты пропорциональности
. В последних формулах коэффициенты пропорциональности 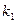 и
и 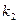 зависят от рода жидкости или газа и их температуры.
зависят от рода жидкости или газа и их температуры.
Наблюдения показывают, что сила сопротивления движению в жидкостях или газах в значительной степени зависит также от формы движущегося тела. Геометрическую форму тела, при которой сила сопротивления движению со стороны среды мала, принято называть обтекаемой.
 Остановимся подробнее на силе трения качения. Если на цилиндр радиуса
Остановимся подробнее на силе трения качения. Если на цилиндр радиуса  (рисунок 10.3) действует горизонтальная внешняя сила
(рисунок 10.3) действует горизонтальная внешняя сила  , то возникающая в месте контакта цилиндра и опорной плоскости сила реакции
, то возникающая в месте контакта цилиндра и опорной плоскости сила реакции  смещена в сторону действия силы
смещена в сторону действия силы  из-за деформации поверхностей соприкосновения. При равновесии цилиндра сумма моментов сил, действующих на цилиндр, равна нулю: момент силы
из-за деформации поверхностей соприкосновения. При равновесии цилиндра сумма моментов сил, действующих на цилиндр, равна нулю: момент силы  относительно точки
относительно точки  уравновешивается моментом силы реакции опоры
уравновешивается моментом силы реакции опоры
 . (10.8)
. (10.8)
При увеличении внешней силы увеличивается и момент силы реакции опоры. Наибольшее значение  достигается в момент начала качения цилиндра по плоскости.
достигается в момент начала качения цилиндра по плоскости.
Для наибольшего значения момента 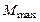 силы реакции опоры, препятствующей качению, установлены следующие приближенные законы:
силы реакции опоры, препятствующей качению, установлены следующие приближенные законы:
1 Наибольший момент 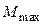 в широких пределах не зависит от радиуса колеса
в широких пределах не зависит от радиуса колеса 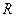 .
.
2 Значение максимального момента 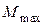 пропорционально нормальному давлению. В нашем случае
пропорционально нормальному давлению. В нашем случае
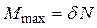 , (10.9)
, (10.9)
где коэффициент пропорциональности 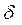 называют коэффициентом трения качения. Из формулы (10.9) видно, что
называют коэффициентом трения качения. Из формулы (10.9) видно, что  имеет размерность длины.
имеет размерность длины.
Коэффициент трения качения  зависит от материала цилиндра и плоскости, состояния их поверхностей и физических параметров (температура, давление и т.д.). Зачастую коэффициент
зависит от материала цилиндра и плоскости, состояния их поверхностей и физических параметров (температура, давление и т.д.). Зачастую коэффициент  при качении можно считать не зависящим от угловой скорости качения и скорости скольжения по плоскости.
при качении можно считать не зависящим от угловой скорости качения и скорости скольжения по плоскости.
Перечисленные выше положения справедливы для не очень больших нормальных давлений и для относительно слабо деформирующихся материалов.
В технике для характеристики трения качения обычно пользуются минимальной величиной F, необходимой для перекатывания цилиндра, приложенной к его оси в горизонтальном направлении:
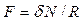 . (10.10)
. (10.10)
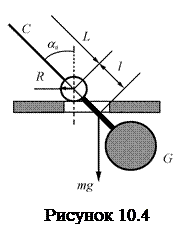
 В данной работе для экспериментального определения коэффициента
В данной работе для экспериментального определения коэффициента  используется маятник, схема которого представлена на рисунке 10.4.
используется маятник, схема которого представлена на рисунке 10.4.
Цилиндр радиуса 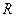 находится на горизонтальной плите. Стрелка
находится на горизонтальной плите. Стрелка 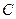 прикреплена к цилиндру сверху. Снизу к системе прикреплен груз G. При отклонении груза от положения равновесия система может совершать колебания. Колебания системы будут затухающими в первую очередь из-за противодействия момента сил трения качения. Движение цилиндра при этом — поступательно-вращательное.
прикреплена к цилиндру сверху. Снизу к системе прикреплен груз G. При отклонении груза от положения равновесия система может совершать колебания. Колебания системы будут затухающими в первую очередь из-за противодействия момента сил трения качения. Движение цилиндра при этом — поступательно-вращательное.
Коэффициент трения качения 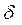 можно определить по скорости затухания колебаний.
можно определить по скорости затухания колебаний.
Рассматривая процесс колебаний, воспользуемся законом сохранения энергии. Пусть маятник в начальный момент отклонили на угол 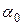 от положения равновесия и отпустили. Через период (одно колебание) угол отклонения будет равен
от положения равновесия и отпустили. Через период (одно колебание) угол отклонения будет равен 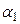 , через n периодов —
, через n периодов — 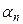 соответственно, как показано на рисунке 10.5. Потенциальная энергия маятника через n периодов
соответственно, как показано на рисунке 10.5. Потенциальная энергия маятника через n периодов
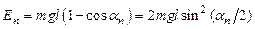 , (10.11)
, (10.11)
где m — масса маятника,
l — расстояние между центром тяжести маятника и осью цилиндра.
Уменьшение потенциальной энергии за первый период будет:
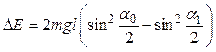 .
.
При малых углах  получим
получим
 . (10.12)
. (10.12)
Пренебрегая работой сил сопротивления воздуха и считая, что изменение энергии вызвано работой момента трения качения, можно написать:
 , (10.13)
, (10.13)
где 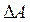 — работа момента M силы реакции опоры Т при повороте на угол
— работа момента M силы реакции опоры Т при повороте на угол  .
.
За один полный период колебаний угол поворота составляет
 ,
,
где 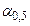 — угол отклонения после одного полупериода (рисунок 5).
— угол отклонения после одного полупериода (рисунок 5).
Считая в среднем
 ,
,
можно записать
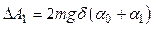 . (10.14)
. (10.14)
Приравнивая (10.12) и (10.14), получим:
 .
.
Аналогичные соотношения можно получить для следующих периодов. Для полных n периодов имеем
 . (10.15)
. (10.15)
Таким образом, определив начальный и конечный углы, а также подсчитав число колебаний, можно оценить коэффициент трения качения  .
.
Экспериментальная часть
Описание экспериментальной установки
 Схема установки представлена на рисунке 10.6. На столике установлен маятник. Маятник состоит, в свою очередь, из цилиндра, сделанного из нержавеющей стали, стрелки и массивного груза. Начальное отклонение маятника производится вручную до фиксатора, положение которого можно менять. Шкала служит для измерения угла отклонения маятника с помощью стрелки. Положение шкалы можно регулировать, совмещая конец стрелки покоящегося маятника с нулем шкалы. Датчик, подсоединенный к таймеру (на рисунке не показан), позволяет отсчитывать число полных колебаний маятника. Под цилиндр к столику могут крепиться пластинки из различных исследуемых материалов.
Схема установки представлена на рисунке 10.6. На столике установлен маятник. Маятник состоит, в свою очередь, из цилиндра, сделанного из нержавеющей стали, стрелки и массивного груза. Начальное отклонение маятника производится вручную до фиксатора, положение которого можно менять. Шкала служит для измерения угла отклонения маятника с помощью стрелки. Положение шкалы можно регулировать, совмещая конец стрелки покоящегося маятника с нулем шкалы. Датчик, подсоединенный к таймеру (на рисунке не показан), позволяет отсчитывать число полных колебаний маятника. Под цилиндр к столику могут крепиться пластинки из различных исследуемых материалов.
В связи с тем, что цилиндр при качении движется вращательно-поступательно, необходимо уточнить связь угла поворота цилиндра 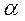 с показаниями стрелки маятника, отсчитываемыми по линейной шкале S.
с показаниями стрелки маятника, отсчитываемыми по линейной шкале S.
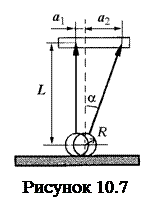 Смещение конца стрелки можно представить в виде суммы двух смещений: поступательного движения оси цилиндра
Смещение конца стрелки можно представить в виде суммы двух смещений: поступательного движения оси цилиндра  и вращательной компоненты
и вращательной компоненты 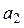 поворота конца стрелки относительно центра цилиндра (рисунок 10.7).
поворота конца стрелки относительно центра цилиндра (рисунок 10.7).
Для суммарного отклонения х конца стрелки от нулевого деления получим
 ,
,
где R — радиус цилиндра х,
L — расстояние от оси цилиндра до шкалы (длина стрелки),
 — угол поворота маятника.
— угол поворота маятника.
При малых углах  , и можно считать
, и можно считать
 ,
, 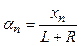 ,
,
где  и
и  — начальная и конечная амплитуды отклонения стрелки по шкале S. Тогда расчетную формулу (10.15) можно окончательно представить в виде
— начальная и конечная амплитуды отклонения стрелки по шкале S. Тогда расчетную формулу (10.15) можно окончательно представить в виде
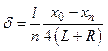 , (10.16)
, (10.16)
где n — число периодов колебаний маятника за время измерения.
Проведение эксперимента
Измерения
2 Определите общую длину стрелки L как сумму длины телескопической части стрелки и радиуса цилиндра. 3 Установите маятник в такое положение, чтобы в равновесии конец стрелки… 4 Для вычисления коэффициента трения качения по формуле (10.16) необходимо измерить начальное отклонение стрелки…Обработка результатов
2 Определите среднеквадратичное отклонение числа колебаний для каждой серии измерений (каждой пластинки): . (10.17) С помощью формулы (10.15) определите величины коэффициентов трения качения для трех пластин.Основные итоги работы
В результате выполнения работы должны быть получены значения коэффициентов трения качения для различных пар материалов, рассчитаны погрешности, проведен анализ причин их возникновения.
Контрольные вопросы
1 Почему возникает эффект трения?
2 Дайте определение коэффициента трения качения.
3 В чем отличие трения качения от трения скольжения?
4 Сформулируйте приближенные законы, описывающие эффект трения качения.
5 От чего зависит коэффициент трения качения?
6 Выведите расчетную формулу (10.16).
7 Цилиндр радиуса R находится на горизонтальной плоскости. Коэффициент трения скольжения поверхностей —  , коэффициент трения качения —
, коэффициент трения качения — 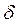 . Во сколько раз отличается сила F1, необходимая для того, чтобы цилиндр начал движение, от силы F2, необходимой для начала проскальзывания? Силы приложены к центру цилиндра горизонтально.
. Во сколько раз отличается сила F1, необходимая для того, чтобы цилиндр начал движение, от силы F2, необходимой для начала проскальзывания? Силы приложены к центру цилиндра горизонтально.
Рекомендуемая литература
10.4.1 Зисман, Г.А. Курс общей физики: в 3 т. / Г.А. Зисман, О.М. Тодес. – СПб.: Лань, 2007. – Т.1: Механика. Молекулярная физика. Колебания и волны. – 340 с. - ISBN 978-5-8114-0753-8.
10.4.2 Иродов, И.Е. Механика. Основные законы механики / И.Е.Иродов. - М.: Бином, 2009. – 310 с. - ISBN 978-5-9963-0063-1.
10.4.3 Савельев, И.В. Курс общей физики: в 5 кн. / И.В.Савельев. – М.: АСТРЕЛЬ: АСТ, 2005. – Кн. 1: Механика. – 336 с. - ISBN 5-271-01034-1.
10.4.4 Сивухин, Д.В. Общий курс физики: в 3 т. / Д.В.Сивухин. - М.: Физматлит, 2002. – Т. 1: Механика. – 560 с. - ISBN 5-89155-078-4.
10.4.5 Трофимова, Т.И. Физика в таблицах и формулах / Т.И. Трофимова. – М.: Академия, 2006. – 448 с. - ISBN 5-7695-2277-1.
Лабораторная работа №11. Тензор инерции твердого тела
Цель работы: 1) изучить тензор инерции твердого тела;
2) экспериментально получить сечение эллипсоида инерции плоскостью 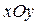 исследуемого тела.
исследуемого тела.
Теоретическая часть
 Вычислим момент инерции
Вычислим момент инерции  твердого тела относительно произвольной оси
твердого тела относительно произвольной оси  (рисунок 11.1), проходящей через начало координат
(рисунок 11.1), проходящей через начало координат  . Пусть
. Пусть 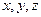 координаты. Разложим радиус-вектор
координаты. Разложим радиус-вектор  элемента массы тела
элемента массы тела  на составляющие вдоль оси
на составляющие вдоль оси  и перпендикулярную к ней:
и перпендикулярную к ней:  . По определению момента инерции
. По определению момента инерции

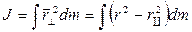 .
.
Если 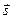 - единичный вектор вдоль оси
- единичный вектор вдоль оси  , то
, то 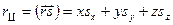 . Кроме того,
. Кроме того, 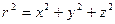 . Учтя эти соотношения, а также соотношение
. Учтя эти соотношения, а также соотношение  , получим
, получим
 , (11.1)
, (11.1)
где 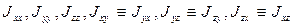 - постоянные, определяемые выражениями
- постоянные, определяемые выражениями
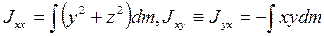 ,
,
 , (11.2)
, (11.2)
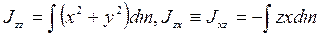 .
.
Совокупность девяти величин
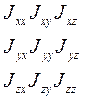 (11.3)
(11.3)
называются тензором инерции тела относительно точки  , а сами эти величины – компонентами тензора. Тензор инерции симметричен, т.е.
, а сами эти величины – компонентами тензора. Тензор инерции симметричен, т.е. 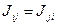 . Формулу (11.1) в таком случае можно переписать в виде
. Формулу (11.1) в таком случае можно переписать в виде
 . (11.4)
. (11.4)
Если известны для какой-либо координатной системы все шесть компонентов тензора инерции, то по формуле (11.1) или (11.4) можно вычислить момент инерции тела относительно произвольной оси, проходящей через начало координат  . Момент инерции относительно другой оси, не проходящей через начало координат, можно вычислить с помощью теоремы Гюйгенса-Штейнера.
. Момент инерции относительно другой оси, не проходящей через начало координат, можно вычислить с помощью теоремы Гюйгенса-Штейнера.
Формула (11.4) допускает наглядную геометрическую интерпретацию. Через начало координат  будем проводить прямые во всевозможных направлениях и на них откладывать отрезки длиной
будем проводить прямые во всевозможных направлениях и на них откладывать отрезки длиной 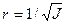 . Геометрическим местом концов таких отрезков будет некоторая поверхность. Найдем ее уравнение. Согласно построению радиус-вектор точки, лежащей на этой поверхности, определяется выражением
. Геометрическим местом концов таких отрезков будет некоторая поверхность. Найдем ее уравнение. Согласно построению радиус-вектор точки, лежащей на этой поверхности, определяется выражением  , а координаты той же точки - выражением
, а координаты той же точки - выражением  . Исключая с помощью этих соотношений величины
. Исключая с помощью этих соотношений величины  , из (11.4), получим уравнение искомой поверхности
, из (11.4), получим уравнение искомой поверхности
 . (11.5)
. (11.5)
Эта поверхность второго порядка, очевидно, является эллипсоидом, так как момент инерции  , а с ним и длина радиуса-вектора
, а с ним и длина радиуса-вектора  имеют конечные значения, каково бы ни было направление оси
имеют конечные значения, каково бы ни было направление оси 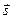 . Она называется эллипсоидом инерции тела относительно точки
. Она называется эллипсоидом инерции тела относительно точки 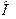 , являющейся его центром. При перемещении начала координат
, являющейся его центром. При перемещении начала координат  относительно тела будет меняться и эллипсоид инерции тела. Если в качестве
относительно тела будет меняться и эллипсоид инерции тела. Если в качестве  взят центр масс тела, то и соответствующий эллипсоид называется центральным.
взят центр масс тела, то и соответствующий эллипсоид называется центральным.
Предположим, что твердое тело закреплено таким образом, что может вращаться вокруг некоторой неподвижной точки  . Введем в лабораторной системе отсчета декартову систему координат
. Введем в лабораторной системе отсчета декартову систему координат  с началом в этой точке. Произвольная
с началом в этой точке. Произвольная 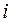 -я точка твердого тела массы
-я точка твердого тела массы  будет иметь скорость
будет иметь скорость 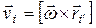 , где
, где 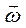 — вектор угловой скорости вращения твердого тела, а
— вектор угловой скорости вращения твердого тела, а  — радиус-вектор, проведенный из начала координат в точку, где в данный момент времени находится
— радиус-вектор, проведенный из начала координат в точку, где в данный момент времени находится 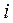 -я материальная точка. Момент импульса этой точки равен по определению
-я материальная точка. Момент импульса этой точки равен по определению
 . (11.6)
. (11.6)
Векторы  ,
,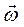 ,
,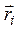
 можно рассматривать как в лабораторной системе координат
можно рассматривать как в лабораторной системе координат  , так и в системе координат
, так и в системе координат  , жестко связанной с телом.
, жестко связанной с телом.
Перепишем выражение для  в проекциях на оси системы координат
в проекциях на оси системы координат 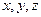 , начало которой лежит в точке
, начало которой лежит в точке  . Учитывая, что
. Учитывая, что
 , а
, а 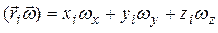 ,
,
получаем

 (11.7)
(11.7)

Момент импульcа вcего тела pавен cумме моментов импульcов вcеx элементаpныx маcc:
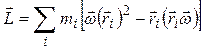 . (11.8)
. (11.8)
Учитывая (11.7), соотношение (11.8) можно пеpепиcать в пpоекцияx на кооpдинатные оcи в виде:
 ,
,
 , (11.9)
, (11.9)
 .
.
Совокупность девяти величин  определяет тензор инерции
определяет тензор инерции
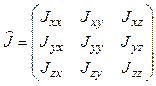 . (11.10)
. (11.10)
Проекции момента импульса на оси координат (11.9) удобно записать в матричном виде. В рассматриваемом случае начало декартовой системы координат совпадает с точкой  (центром вращения), поэтому из (11.7) и (11.8) получаем
(центром вращения), поэтому из (11.7) и (11.8) получаем
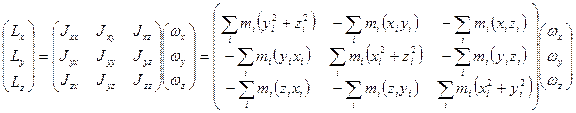 (11.11)
(11.11)
Отметим, что выражение (11.8) принимает точно такой же вид, если векторы 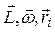 проецировать на оси лабораторной системы координат
проецировать на оси лабораторной системы координат  . Отличие заключается в том, что в покоящейся лабораторной системе координат постоянно меняются координаты
. Отличие заключается в том, что в покоящейся лабораторной системе координат постоянно меняются координаты  каждого бесконечно малого элемента тела, поэтому и компоненты тензора
каждого бесконечно малого элемента тела, поэтому и компоненты тензора  меняются со временем. В выбранной системе координат
меняются со временем. В выбранной системе координат  радиус-вектор
радиус-вектор 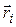 — неизменная величина, а проекции угловой скорости
— неизменная величина, а проекции угловой скорости  меняются со временем.
меняются со временем.
Диагональные элементы тензора 
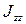 называются осевыми моментами инерции.
называются осевыми моментами инерции. Недиагональные элементы
Недиагональные элементы 
 называются центробежными моментами инерции.
называются центробежными моментами инерции.
Тензор инерции является симметричным, так как 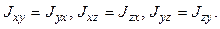 Симметричный тензор всегда можно привести к диагональному виду, т.е. выбрать такую систему координат, определяемую формой тела, в которой все недиагональные элементы будут равны нулю. Соответствующие направления координатных осей называются главными осями инерции, а величины
Симметричный тензор всегда можно привести к диагональному виду, т.е. выбрать такую систему координат, определяемую формой тела, в которой все недиагональные элементы будут равны нулю. Соответствующие направления координатных осей называются главными осями инерции, а величины  — главными моментами инерции. Оси, проходящие через центр масс тела, будем называть центральными осями, а оси, проходящие через центр масс и одновременно являющиеся главными, будем называть главными центральными осями.
— главными моментами инерции. Оси, проходящие через центр масс тела, будем называть центральными осями, а оси, проходящие через центр масс и одновременно являющиеся главными, будем называть главными центральными осями.
Связь между моментом инерции и компонентами тензора инерции. Рассмотрим вращение твердого тела относительно некоторой закрепленной оси 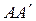 , имеющей произвольное направление в пространстве. Представим радиус-вектор
, имеющей произвольное направление в пространстве. Представим радиус-вектор 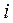 -й материальной точки массы
-й материальной точки массы 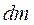 в виде
в виде 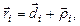 где
где  (вектор
(вектор  направлен вдоль оси в соответствии с правилом правого винта как показано на рисунке 2). Так как ось
направлен вдоль оси в соответствии с правилом правого винта как показано на рисунке 2). Так как ось 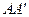 закреплена, то линейная скорость точки перпендикулярна этой оси и равна
закреплена, то линейная скорость точки перпендикулярна этой оси и равна 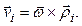 . Предположим, что в жестко связанной с телом системе координат
. Предположим, что в жестко связанной с телом системе координат 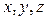 ось
ось  (рисунок 11.2) лежит в плоскости
(рисунок 11.2) лежит в плоскости  , а тензор инерции имеет диагональный вид
, а тензор инерции имеет диагональный вид
 .
.
 Вектор угловой скорости будет иметь компоненты
Вектор угловой скорости будет иметь компоненты 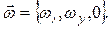 В соответствии с (11.9)
В соответствии с (11.9)  Отсюда следует, что в общем случае
Отсюда следует, что в общем случае  направление вектора момента импульса, даже при вращении вокруг закрепленной оси, не совпадает с направлением вектора угловой скорости. Кроме того, в рассматриваемом случае положение вектора
направление вектора момента импульса, даже при вращении вокруг закрепленной оси, не совпадает с направлением вектора угловой скорости. Кроме того, в рассматриваемом случае положение вектора 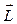 жестко связано с телом. Поэтому при вращении тела вектор момента импульса меняет свое направление в пространстве: конец этого вектора описывает окружность с центром, лежащим на оси
жестко связано с телом. Поэтому при вращении тела вектор момента импульса меняет свое направление в пространстве: конец этого вектора описывает окружность с центром, лежащим на оси 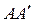 . Вектор
. Вектор 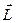 так же, как и радиус-вектор, удобно разложить на две составляющие — одну, совпадающую с вектором угловой скорости
так же, как и радиус-вектор, удобно разложить на две составляющие — одну, совпадающую с вектором угловой скорости 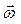 , и другую, перпендикулярную к нему, т.е.
, и другую, перпендикулярную к нему, т.е. 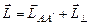 . В этом случае векторное уравнение моментов можно разбить на два скалярных уравнения:
. В этом случае векторное уравнение моментов можно разбить на два скалярных уравнения:
 (11.12)
(11.12)
 (11.13)
(11.13)
В уравнении (11.12) 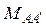 — это проекция момента внешних сил на ось
— это проекция момента внешних сил на ось  (включая силы трения в оси). Это уравнение полностью описывает вращательное движение твердого тела вокруг закрепленной оси. После представления
(включая силы трения в оси). Это уравнение полностью описывает вращательное движение твердого тела вокруг закрепленной оси. После представления  , где
, где 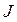 — момент инерции тела относительно закрепленной оси, уравнение (11.12) принимает вид
— момент инерции тела относительно закрепленной оси, уравнение (11.12) принимает вид
 .
.
 В уравнении (11.13)
В уравнении (11.13)  — это перпендикулярная проекция суммарного момента внешних сил, включая силы упругости, действующие на тело со стороны оси. Наличие этого момента приводит к повороту вектора
— это перпендикулярная проекция суммарного момента внешних сил, включая силы упругости, действующие на тело со стороны оси. Наличие этого момента приводит к повороту вектора 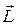 вокруг
вокруг 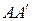 . Уравнение (11.13) необходимо решать, если встает вопрос о деформациях, возникающих в оси.
. Уравнение (11.13) необходимо решать, если встает вопрос о деформациях, возникающих в оси.
Значение момента инерции 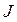 твердого тела относительно некоторой оси, можно найти, зная направление этой оси в пространстве и значения компонент тензора инерции. Выразим момент инерции относительно закрепленной оси
твердого тела относительно некоторой оси, можно найти, зная направление этой оси в пространстве и значения компонент тензора инерции. Выразим момент инерции относительно закрепленной оси  , проходящей через начало координат, через компоненты тензора
, проходящей через начало координат, через компоненты тензора  . Пусть система координат
. Пусть система координат 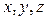 расположена произвольным образом относительно тела так, что все компоненты тензора
расположена произвольным образом относительно тела так, что все компоненты тензора являются ненулевыми.
являются ненулевыми.
Воспользуемся соотношением  С учетом (11.9) и того, что
С учетом (11.9) и того, что

 ,
,
где 
 — углы, определяющие положение оси
— углы, определяющие положение оси 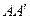 относительно осей координат (рисунок 11.3), получим
относительно осей координат (рисунок 11.3), получим
 (11.14)
(11.14)
Уравнение (11.14) может быть использовано и для решения обратной задачи — определения компонент тензора инерции  через известные значения моментов инерции
через известные значения моментов инерции 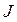 относительно нескольких различных закрепленных осей.
относительно нескольких различных закрепленных осей.
Используемая в лабораторной работе установка удобна для определения моментов инерции “плоских тел” — т.е. таких тел, толщина которых значительно меньше их поперечных размеров. При этом одну из осей (например, ось  ) связанной с телом системы координат удобно направить перпендикулярно плоскости тела. Оси
) связанной с телом системы координат удобно направить перпендикулярно плоскости тела. Оси  и
и 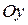 находятся в плоскости тела и их направления произвольны, начало координат совпадает с центром масс тела и находится на оси вращения (рисунок 4). При этом один из направляющих косинусов (
находятся в плоскости тела и их направления произвольны, начало координат совпадает с центром масс тела и находится на оси вращения (рисунок 4). При этом один из направляющих косинусов ( ) равен нулю, и вместо (11.14) получим
) равен нулю, и вместо (11.14) получим
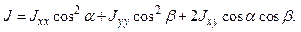
 (11.15)
(11.15)
 Величина
Величина 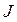 — момент инерции данного тела относительно оси, проходящей через его центр масс. При повороте системы координат (осей
— момент инерции данного тела относительно оси, проходящей через его центр масс. При повороте системы координат (осей  и
и 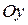 ) в своей плоскости, величина момента инерции
) в своей плоскости, величина момента инерции 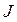 не изменяется, но каждой ориентации осей соответствуют свои значения компонент тензора инерции
не изменяется, но каждой ориентации осей соответствуют свои значения компонент тензора инерции  и
и 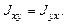
При определенном выборе системы координат, когда направления осей  и
и  совпадают с главными осями инерции тела,
совпадают с главными осями инерции тела, 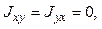 и вместо (11.15) имеем
и вместо (11.15) имеем
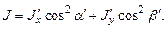 (11.15а)
(11.15а)
В последнем соотношении  и
и 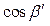 — направляющие косинусы выбранной ранее оси вращения в новых осях координат
— направляющие косинусы выбранной ранее оси вращения в новых осях координат  ,
, ,
,  и
и 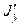 — компоненты тензора инерции в системе координат, оси которой совпадают по направлению с главными осями инерции. Выберем на оси вращения некоторую точку
— компоненты тензора инерции в системе координат, оси которой совпадают по направлению с главными осями инерции. Выберем на оси вращения некоторую точку 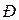 , находящуюся на расстоянии
, находящуюся на расстоянии 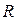 от начала координат и имеющую координаты
от начала координат и имеющую координаты  . Пусть величина
. Пусть величина 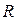 численно равна
численно равна  . При этом
. При этом 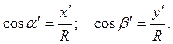 Подставив эти величины в (11.15а), получим
Подставив эти величины в (11.15а), получим
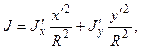
или
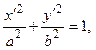 (11.16)
(11.16)
где  , a и b являются постоянными величинами.
, a и b являются постоянными величинами.
Уравнение (11.16) является каноническим уравнением эллипса в координатах 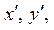 полуоси которого
полуоси которого  .
.
Эллипс (11.16) является сечением эллипсоида инерции плоскостью  Эллипсоидом инерции называется поверхность, характеризующая величины моментов инерции твердого тела относительно множества возможных осей вращения, проходящих через одну точку (в данном случае через центр масс тела). При этом для каждого направления вдоль оси
Эллипсоидом инерции называется поверхность, характеризующая величины моментов инерции твердого тела относительно множества возможных осей вращения, проходящих через одну точку (в данном случае через центр масс тела). При этом для каждого направления вдоль оси  откладываются отрезки, численно равные величине
откладываются отрезки, численно равные величине 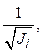 где
где  — момент инерции тела относительно оси
— момент инерции тела относительно оси  Концы этих отрезков образуют поверхность, называемую эллипсоидом инерции (трехмерное уравнение эллипсоида инерции может быть получено из (11.14)).
Концы этих отрезков образуют поверхность, называемую эллипсоидом инерции (трехмерное уравнение эллипсоида инерции может быть получено из (11.14)).
Определение компонент тензора инерции.Пусть исследуемое тело имеет форму, показанную на рисунке 11.5. Точка  — центр масс тела. Оси
— центр масс тела. Оси 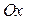 и
и  выбраны произвольно. Тело закреплено в рамке крутильного маятника так, что точка
выбраны произвольно. Тело закреплено в рамке крутильного маятника так, что точка  лежит на оси вращения, а положение тела характеризуется углом
лежит на оси вращения, а положение тела характеризуется углом 
 Если тело закреплено в рамке так, как показано на рисунке 6а, то
Если тело закреплено в рамке так, как показано на рисунке 6а, то  и
и  Из (11.15) получаем
Из (11.15) получаем
 (11.17)
(11.17)
При закреплении тела, соответствующем рисунку 11.6,б,  и
и И, следовательно, из (11.15)
И, следовательно, из (11.15)
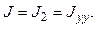 (11.18)
(11.18)
При повороте тела в своей плоскости на угол  (рисунок 11.6,в) и –
(рисунок 11.6,в) и –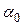 (рисунок 11.6,г) относительно оси вращения получаем, соответственно,
(рисунок 11.6,г) относительно оси вращения получаем, соответственно,
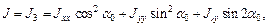 (11.19)
(11.19)
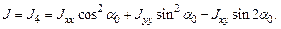 (11.20)
(11.20)
Из (11.19) и (11.20) следует, что
 или
или
 (11.21)
(11.21)
Из (11.15) можно получить, что при 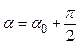
 (11.22)
(11.22)
Складывая (11.19) и (11.22), получаем
 (11.23)
(11.23)
Экспериментальное определение величин 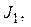

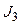 и
и 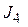 дает возможность найти четыре отличных от нуля компоненты тензора инерции плоского тела:
дает возможность найти четыре отличных от нуля компоненты тензора инерции плоского тела:  для заданной системы координат. Если оси координат
для заданной системы координат. Если оси координат 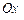 и
и  совпадают с главными осями инерции тела, то
совпадают с главными осями инерции тела, то 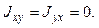 Соотношение (11.23) может служить проверкой правильности проведенного эксперимента.
Соотношение (11.23) может служить проверкой правильности проведенного эксперимента.
Экспериментальная часть
Экспериментальное определение момента инерции относительно закрепленной оси. Рассмотрим колебания крутильного маятника, представляющего собой сложное тело, состоящее из рамки, закрепленной на вертикальной упругой проволоке, и исследуемого тела (рисунок 11.7). Действие момента сил упругости приводит к возникновению колебаний всей системы с периодом
 (11.24)
(11.24)
где D — коэффициент упругости подвеса,
 — момент инерции рамки с исследуемым телом.
— момент инерции рамки с исследуемым телом.
Из соотношения (11.24) можно найти момент инерции  :
:
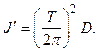 (11.25)
(11.25)
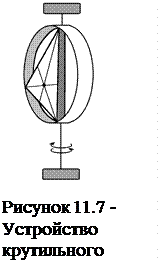 Определяя период колебаний пустой рамки
Определяя период колебаний пустой рамки  , можно найти момент инерции маятника без тела
, можно найти момент инерции маятника без тела 
 (11.26)
(11.26)
Для момента инерции исследуемого тела относительно фиксированной оси вращения получаем:
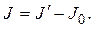 (11.27)
(11.27)
Меняя положение тела относительно рамки, можно определять моменты инерции для осей вращения, имеющих различное направление относительно тела.
Экспериментальная установка
 Экспериментальная установка показана на рисунке 11.8. Она состоит из стойки и рамки, закрепленной на упругом подвесе. Исследуемые тела поочередно крепятся в рамке с помощью винта. Конструкция крепления рамки на подвесе такова, что рамка может поворачиваться вокруг горизонтальной оси и фиксироваться в различных положениях. В работе изучаются тензоры инерции для нескольких “плоских” тел, имеющих разную форму: малых по толщине параллелепипеда, треугольной призмы и полудиска. Система координат, относительно которой определяется момент инерции тела, жестко связана с телом, а, следовательно, и с рамкой. На рамке имеется шкала, позволяющая определять углы между осью вращения и осями системы координат, связанной с телом.
Экспериментальная установка показана на рисунке 11.8. Она состоит из стойки и рамки, закрепленной на упругом подвесе. Исследуемые тела поочередно крепятся в рамке с помощью винта. Конструкция крепления рамки на подвесе такова, что рамка может поворачиваться вокруг горизонтальной оси и фиксироваться в различных положениях. В работе изучаются тензоры инерции для нескольких “плоских” тел, имеющих разную форму: малых по толщине параллелепипеда, треугольной призмы и полудиска. Система координат, относительно которой определяется момент инерции тела, жестко связана с телом, а, следовательно, и с рамкой. На рамке имеется шкала, позволяющая определять углы между осью вращения и осями системы координат, связанной с телом.
Установка снабжена системой автоматического отсчета времени и числа периодов, включающей в себя таймер и фотоэлектронный датчик.
Проведение эксперимента
Упражнение 1. Определение коэффициента упругости подвеса и момента инерции пустой рамки
Определение упругости подвеса осуществляется из результатов изучения колебаний параллелепипеда, закрепленного в рамке перпендикулярно оси вращения. Предполагается, что предварительно измерена его длина и масса и вычислен его момент инерции относительно оси вращения, а также определены погрешности этих величин (результаты измерений и расчетов необходимо внести в таблицу 11.1)
Таблица 11.1
| Длина параллелепипеда а = | Sа= |
| Толщина параллелепипеда с = | Sс = |
| Масса параллелепипеда m = | Sm = |
| Момент инерции параллелепипеда относительно оси, проходящей через центр масс и перпендикулярной ширине параллелепипеда J = | SJ = |
Измерения
1 Измерить время  n = 10–20 колебаний пустой рамки. Измерения провести несколько раз, данные занести в таблицу 11.2.
n = 10–20 колебаний пустой рамки. Измерения провести несколько раз, данные занести в таблицу 11.2.
2 Закрепить параллелепипед в рамке так, чтобы ось вращения была перпендикулярна его длине. Измерить время 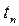 10–20 колебаний рамки с параллелепипедом. Измерения провести несколько раз, данные занести в таблицу 11.2.
10–20 колебаний рамки с параллелепипедом. Измерения провести несколько раз, данные занести в таблицу 11.2.
Обработка результатов
1 Для каждого опыта определить периоды колебаний пустой рамки  и рамки с параллелепипедом
и рамки с параллелепипедом 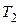 .
.
2 Найти средние арифметические значения  и
и  и выборочные стандартные отклонения для этих величин
и выборочные стандартные отклонения для этих величин . Результаты вычислений внести в таблицу 11.2.
. Результаты вычислений внести в таблицу 11.2.
Таблица 11.2
| Колебания без параллелепипеда | Колебания с параллелепипедом | ||||||||||
| N | tn | n | T0 | <T0> | ST0 | N | tn | n | T2 | <T2> | ST2 |
| ………. |
3 Учитывая, что период колебаний крутильного маятника связан с моментом инерции соотношением (11.24), получаем, что
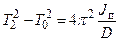 ,
,
где  — вычисленный ранее момент инерции параллелепипеда. Отсюда следует, что
— вычисленный ранее момент инерции параллелепипеда. Отсюда следует, что
 .
.
Используя последнее соотношение, определить коэффициент упругости подвеса, а затем по формуле (11.26) — момент инерции пустой рамки  .
.
Упражнение 2. Определение сечения эллипсоида инерции
Измерения
1 Для выполнения работы необходимо измерить размеры одного из тел по указанию преподавателя (ребра параллелепипеда, стороны треугольной призмы, радиус полудиска). Данные занести в таблицу 11.3.
2 Все тела, исследуемые в данной задаче, закрепляются в рамке благодаря ее конструкции, таким образом, что центр масс лежит на оси вращения. Закрепив в рамке выбранное тело, измерить время  n = 5–10 колебаний. Провести несколько таких измерений. Повернуть рамку на небольшой угол (например, на 10°), и вновь измерить время
n = 5–10 колебаний. Провести несколько таких измерений. Повернуть рамку на небольшой угол (например, на 10°), и вновь измерить время  . Снова повернуть рамку на тот же угол и провести измерения
. Снова повернуть рамку на тот же угол и провести измерения  . Так поступают до полного поворота рамки на 180°. Результаты каждого измерения заносят в таблицу 11.3.
. Так поступают до полного поворота рамки на 180°. Результаты каждого измерения заносят в таблицу 11.3.
Таблица 11.3
| Формы и размеры исследуемого тела | ||||||||
| N | ai | tn | n | T | <Ta> | STa | Ja | 
|
| · · · · · |
Обработка результатов
1 Найти периоды колебаний маятника для каждого значения  , их среднее значение
, их среднее значение  и выборочные стандартные отклонения
и выборочные стандартные отклонения  . Величины занести в таблицу 11.3.
. Величины занести в таблицу 11.3.
2 Определяют моменты инерции исследуемого тела по формулам (11.25)–(11.27) для различных значений 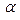 . Данные заносят в таблицу 11.3.
. Данные заносят в таблицу 11.3.
3 Построить в полярных координатах 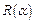 сечение эллипсоида инерции
сечение эллипсоида инерции 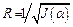 для исследованного тела, считая, что
для исследованного тела, считая, что 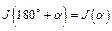 . На этом же графике необходимо нарисовать и исследуемое тело.
. На этом же графике необходимо нарисовать и исследуемое тело.
4 Определить положения рамки, при которых момент инерции принимает максимальное и минимальное значения. Эти положения соответствуют главным центральным осям инерции изучаемого тела.
5 Используя известные формулы, рассчитать величины моментов инерции тела относительно всех трех главных центральных осей и сравнить полученные значения с экспериментальными. При этом теоретическое значение  сравнивается с суммой значений
сравнивается с суммой значений 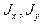 , полученной экспериментально, поскольку для плоских тел
, полученной экспериментально, поскольку для плоских тел 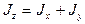 .
.
Упражнение 3. Определение компонент тензора инерции
Для выполнения этого упражнения используется то же тело, что и в упр. 2. На поверхности всех тел, входящих в комплект установки нанесены прямые, проходящие через точку, соответствующую его центру масс и повернутые относительно друг друга на 10°. Каждая из этих прямых может быть выбрана за ось Oх системы координат, связанной с телом. Вначале любую из этих прямых принимают за направление Ох.
Измерения
1 Определить четыре величины момента инерции тела  для случая, когда выбранная ось
для случая, когда выбранная ось 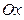 , соответственно, совпадает, перпендикулярна, составляет угол
, соответственно, совпадает, перпендикулярна, составляет угол 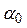 и
и  с осью вращения (
с осью вращения (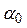 — произвольный угол, например 30° или 50°). Для выполнения этого пункта необходимо произвести измерения, аналогичные проведенным в упр.2. Результаты занести в таблицу 11.4.
— произвольный угол, например 30° или 50°). Для выполнения этого пункта необходимо произвести измерения, аналогичные проведенным в упр.2. Результаты занести в таблицу 11.4.
Приняв за ось  другую прямую, нанесенную на поверхности тела, повторить все измерения п.1 и получить новые значения величин
другую прямую, нанесенную на поверхности тела, повторить все измерения п.1 и получить новые значения величин 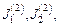
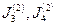 . Полученные результаты занести в таблицу, аналогичную таблице 11.4.
. Полученные результаты занести в таблицу, аналогичную таблице 11.4.
Обработка результатов
Воспользовавшись измеренными величинами  и соотношениями (11.17)–(11.20) определить
и соотношениями (11.17)–(11.20) определить  для двух систем координат, которые использовались в п. 1 и п. 2. Убедиться, что компоненты тензора инерции зависят от выбора системы координат и занести их в таблицу 11.4, указать ориентацию системы координат, для которой они получены.
для двух систем координат, которые использовались в п. 1 и п. 2. Убедиться, что компоненты тензора инерции зависят от выбора системы координат и занести их в таблицу 11.4, указать ориентацию системы координат, для которой они получены.
Таблица 11.4
| Формы и размеры тела | ||||||||||
| N | tn | n | Т | <T> | S<T> | Ji | SJi | |||
| Ось Ох параллельна оси вращения | Jxx | |||||||||
| Ось Ох перпендикулярна оси вращения | Jyy | |||||||||
| Ось Ох составляет угол a0 с осью вращения | Jxy | |||||||||
| Ось Ох составляет угол a0 с осью вращения | ||||||||||
| · · · · · |
Основные итоги работы
Контрольные вопросы
1 Записать уравнение моментов и объяснить смысл входящих в него величин.
2 Какова связь между моментом импульса и угловой скоростью? Что такое тензор инерции?
3 Записать компоненты тензора инерции для простейших систем: тонкая палочка, система материальных точек.
4 Что такое главные оси? Что такое центральные оси? Примеры.
5 Как направлены векторы угловой скорости и момента количества движения тела вокруг закрепленной оси
если ось вращения совпадает с одной из главных осей;
если ось вращения не совпадает ни с одной из главных осей?
6 Связь между компонентами тензора инерции и моментом инерции относительно фиксированной оси.
7 Что такое эллипсоид инерции? Как с помощью эллипсоида инерции определить значение момента инерции тела относительно заданной оси?
Рекомендуемая литература
11.4.1 Зисман, Г.А. Курс общей физики: в 3 т. / Г.А. Зисман, О.М. Тодес. – СПб.: Лань, 2007. – Т.1: Механика. Молекулярная физика. Колебания и волны. – 340 с. - ISBN 978-5-8114-0753-8.
11.4.2 Иродов, И.Е. Механика. Основные законы механики / И.Е.Иродов. - М.: Бином, 2009. – 310 с. - ISBN 978-5-9963-0063-1.
11.4.3 Савельев, И.В. Курс общей физики: в 5 кн. / И.В.Савельев. – М.: АСТРЕЛЬ: АСТ, 2005. – Кн. 1: Механика. – 336 с. - ISBN 5-271-01034-1.
11.4.4 Сивухин, Д.В. Общий курс физики: в 3 т. / Д.В.Сивухин. - М.: Физматлит, 2002. – Т. 1: Механика. – 560 с. - ISBN 5-89155-078-4.
Лабораторная работа №12. Свободные и вынужденные колебания
Цель работы: 1) изучение кинематики и динамики гармонического колебательного движения;
2) изучение свободных и вынужденных колебаний в системе с одной степенью свободы.
Теоретическая часть
В лабораторной работе используется пружинный маятник, тело которого обладает магнитными свойствами и движется в вязкой среде, а внешняя вынуждающая сила создается с помощью переменного магнитного поля. Для анализа движения маятника используется пьезоэлектрический датчик, управление экспериментом и обработка результатов производится с помощью ЭВМ.
Колебания широко распространены в природе. В общем случае под колебаниями понимают движения, в той или иной степени повторяющиеся во времени. По физической природе колебательные процессы разделяют на механические, электромагнитные, электромеханические и т.д. Особую роль в физике играют механические и электромагнитные колебания. С помощью распространяющихся колебаний плотности и давления воздуха (воспринимаемых как звук) и с помощью распространяющихся электромагнитных колебаний (свет) мы получаем большую часть информации об окружающем мире.
Несмотря на различную физическую природу колебаний, их можно описать одинаковыми уравнениями. Если физическая величина  изменяется со временем по гармоническому закону
изменяется со временем по гармоническому закону
 , (12.1)
, (12.1)
колебания называют гармоническими.
Здесь 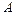 — амплитуда колебаний;
— амплитуда колебаний;
 — круговая (циклическая) частота (
— круговая (циклическая) частота ( — период);
— период);
 — время;
— время;
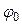 — начальная фаза. Функция
— начальная фаза. Функция  из (12.1) представляет решение дифференциального уравнения
из (12.1) представляет решение дифференциального уравнения
 , (12.2)
, (12.2)
называемого уравнением свободных колебаний (уравнение гармонического осциллятора).
Если уравнения, описывающие колебания, имеют вид линейных дифференциальных уравнений, колебания называются линейными. В реальной системе это соответствуют тем случаям, когда все возникающие силы можно считать линейными функциями координат и скоростей.
Физическую систему, выведенную из состояния равновесия и предоставленную самой себе, в которой изменение одного из параметров 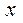 описывается дифференциальным уравнением (12.2), называют классическим гармоническим осциллятором.
описывается дифференциальным уравнением (12.2), называют классическим гармоническим осциллятором.
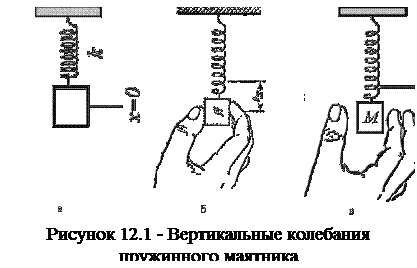 Колебания можно разделить на собственные и вынужденные. В первом из них за счет внешней силы система выводится из состояния устойчивого равновесия, т.е. ей сообщается некоторое достаточное количество энергии, после чего внешние силы полностью отключаются. В этом случае возникают колебания, которые называются собственными колебаниями системы. Если же на систему постоянно действует внешняя сила, то происходят так называемые вынужденные колебания.
Колебания можно разделить на собственные и вынужденные. В первом из них за счет внешней силы система выводится из состояния устойчивого равновесия, т.е. ей сообщается некоторое достаточное количество энергии, после чего внешние силы полностью отключаются. В этом случае возникают колебания, которые называются собственными колебаниями системы. Если же на систему постоянно действует внешняя сила, то происходят так называемые вынужденные колебания.
Рассмотрим колебания гармонического осциллятора на примере пружинного маятника.
Пружинный маятник состоит из тела массы  и легкой пружины с коэффициентом жесткости
и легкой пружины с коэффициентом жесткости 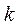 , как показано на рисунке 12.1,а. В общем случае движение пружинного маятника в поле силы тяжести довольно сложно и описывается большим числом степеней свободы. Практический интерес, однако, представляют колебания с одной степенью свободы, когда движение маятника происходит вдоль вертикальной оси. Для возбуждения таких колебаний можно немного растянуть пружину, а затем отпустить маятник (рисунок 12.1 б, в). В этом случае для полного описания колебаний необходимо знать поведение только одной переменной, например, вертикальной координаты центра масс тела маятника. На тело, подвешенное на пружине в поле силы тяжести действуют две силы (без учета сил трения): сила тяготения и упругая сила. Начало координат выберем таким образом, чтобы при
, как показано на рисунке 12.1,а. В общем случае движение пружинного маятника в поле силы тяжести довольно сложно и описывается большим числом степеней свободы. Практический интерес, однако, представляют колебания с одной степенью свободы, когда движение маятника происходит вдоль вертикальной оси. Для возбуждения таких колебаний можно немного растянуть пружину, а затем отпустить маятник (рисунок 12.1 б, в). В этом случае для полного описания колебаний необходимо знать поведение только одной переменной, например, вертикальной координаты центра масс тела маятника. На тело, подвешенное на пружине в поле силы тяжести действуют две силы (без учета сил трения): сила тяготения и упругая сила. Начало координат выберем таким образом, чтобы при 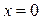 масса
масса 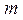 находилась в равновесии. При этом сила тяжести будет скомпенсирована некоторым начальным растяжением пружины и в дальнейшем рассмотрении участвовать не будет.
находилась в равновесии. При этом сила тяжести будет скомпенсирована некоторым начальным растяжением пружины и в дальнейшем рассмотрении участвовать не будет.
При отклонении тела от точки равновесия будет возникать возвращающая сила  . Рассмотрим малые колебания пружинного маятника. Колебания пружинного маятника называют малыми, если сила, возникающая при смещении грузика от положения равновесия, пропорциональна его смещению и направлена в сторону положения равновесия. Для пружинного маятника условия малости колебаний удовлетворяются при смещениях, создающих возвращающую силу у пружины в пределах применимости закона Гука. Уравнение движения пружинного маятника при этом имеет вид
. Рассмотрим малые колебания пружинного маятника. Колебания пружинного маятника называют малыми, если сила, возникающая при смещении грузика от положения равновесия, пропорциональна его смещению и направлена в сторону положения равновесия. Для пружинного маятника условия малости колебаний удовлетворяются при смещениях, создающих возвращающую силу у пружины в пределах применимости закона Гука. Уравнение движения пружинного маятника при этом имеет вид
 . (12.3)
. (12.3)
Сравнивая с (12.2), имеем
 . (12.4)
. (12.4)
В реальных осцилляторах, за счет сил трения, происходит рассеяние (диссипация) запасенной энергии, в результате чего свободные колебания со временем затухают. При движении тела пружинного маятника в вязкой среде, с небольшими скоростями сила трения пропорциональна скорости 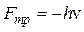 , где
, где 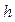 — коэффициент пропорциональности, зависящий от размеров и формы тела, свойств его поверхности и среды. При учете диссипации энергии в уравнении движения необходимо добавить силу трения, и уравнение колебаний будет
— коэффициент пропорциональности, зависящий от размеров и формы тела, свойств его поверхности и среды. При учете диссипации энергии в уравнении движения необходимо добавить силу трения, и уравнение колебаний будет
 . (12.5)
. (12.5)
Решение этого уравнения имеет вид затухающих колебаний
 , (12.6)
, (12.6)
где 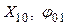 — начальные амплитуда и фаза колебаний,
— начальные амплитуда и фаза колебаний,
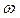 — частота затухающих колебаний,
— частота затухающих колебаний,
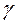 — коэффициент затухания. Действительно, подставим (12.6) в (12.5) и получим:
— коэффициент затухания. Действительно, подставим (12.6) в (12.5) и получим:
 . (12.7)
. (12.7)
Отсюда следует, что (12.6) является решением (12.5) при условии
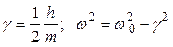 . (12.8)
. (12.8)
Обратите внимание: частота затухающих колебаний (12.8) отличается от частоты собственных 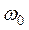 .
.
Используя полученный результат, уравнение колебаний удобно записать в виде:
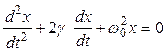 . (12.9)
. (12.9)
Отклонение маятника от положения равновесия в зависимости от времени в соответствии с (12.6) имеет вид, показанный на рисунке 12.2,a. Для малых декрементов затухания колебания близки к гармоническим, при больших 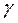 затухание происходит за 1–2 периода. В том случае, когда
затухание происходит за 1–2 периода. В том случае, когда 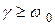 , значение частоты
, значение частоты 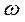 становится мнимым и гармонические колебания не реализуются, происходит апериодический процесс — тело маятника после начального отклонения плавно возвращается в положение равновесия (рисунок 12.2,б). При этом величина
становится мнимым и гармонические колебания не реализуются, происходит апериодический процесс — тело маятника после начального отклонения плавно возвращается в положение равновесия (рисунок 12.2,б). При этом величина 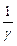 равна времени, за которое амплитуда колебаний затухает в
равна времени, за которое амплитуда колебаний затухает в  раз. Затухание колебаний за период носит название логарифмического декремента затухания
раз. Затухание колебаний за период носит название логарифмического декремента затухания  , его можно определить из соотношения
, его можно определить из соотношения
|
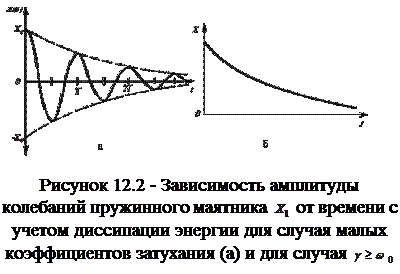
 , (12.10)
, (12.10)
|
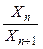 — отношение амплитуд двух последовательных колебаний.
— отношение амплитуд двух последовательных колебаний.
Рассмотрим теперь колебания пружинного маятника, которые возникают под действием внешней периодической силы  в системе с одной степенью свободы. Вынужденные колебания в случае гармонического воздействия описываются уравнением
в системе с одной степенью свободы. Вынужденные колебания в случае гармонического воздействия описываются уравнением
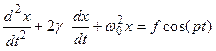 , (12.11)
, (12.11)
где 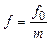 — нормированная амплитуда,
— нормированная амплитуда,
 — частота вынуждающей силы.
— частота вынуждающей силы.
Решение уравнения (12.11) имеет вид
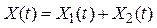 , (12.12)
, (12.12)
где 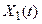 соответствует затухающим собственным колебаниям (см. уравнение (12.6)),
соответствует затухающим собственным колебаниям (см. уравнение (12.6)),
 — вынужденным колебаниям на частоте вынуждающей силы:
— вынужденным колебаниям на частоте вынуждающей силы:
 , (12.13)
, (12.13)
где
 (12.14)
(12.14)
— зависящая от частоты амплитуда вынужденных колебаний,
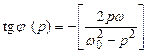 (12.15)
(12.15)
— фаза колебаний.
Величина  в данном случае представляет собой отставание по фазе вынужденного колебания от обуславливающей его вынуждающей силы.
в данном случае представляет собой отставание по фазе вынужденного колебания от обуславливающей его вынуждающей силы.
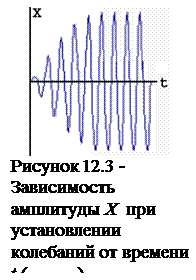 Выражения для амплитуды и фазы колебаний
Выражения для амплитуды и фазы колебаний  , так же, как и для свободных колебаний, можно определить непосредственной подстановкой (12.13) в (12.14). При малых декрементах затухания на частотах вблизи частоты
, так же, как и для свободных колебаний, можно определить непосредственной подстановкой (12.13) в (12.14). При малых декрементах затухания на частотах вблизи частоты  свободных колебаний маятника амплитуда колебаний резко возрастает. Это явление получило название резонанса. Более точно значение резонансной частоты
свободных колебаний маятника амплитуда колебаний резко возрастает. Это явление получило название резонанса. Более точно значение резонансной частоты  можно получить из (12.14), проводя исследование функции на экстремум
можно получить из (12.14), проводя исследование функции на экстремум
 . (12.16)
. (12.16)
 Слагаемое
Слагаемое  играет заметную роль только в начальной стадии процесса, при установлении колебаний (рисунок 12.3). С течением времени из-за экспоненциального множителя
играет заметную роль только в начальной стадии процесса, при установлении колебаний (рисунок 12.3). С течением времени из-за экспоненциального множителя 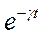 роль слагаемого
роль слагаемого 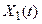 уменьшается и через некоторое время им можно пренебречь, сохраняя в решении только слагаемое
уменьшается и через некоторое время им можно пренебречь, сохраняя в решении только слагаемое 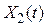 .
.
 Типичные амплитудно-частотные и фазо-частотные характеристики показаны на рисунке 12.4.
Типичные амплитудно-частотные и фазо-частотные характеристики показаны на рисунке 12.4.
Вместе с логарифмическим декрементом затухания 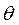 широко пользуются величиной
широко пользуются величиной 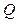 , которая называется добротностью системы
, которая называется добротностью системы 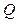 . Она определяется как отношение амплитуды смещения при резонансе
. Она определяется как отношение амплитуды смещения при резонансе 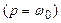
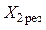 к амплитуде смещения
к амплитуде смещения 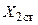 при
при 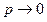 . Учитывая определения коэффициента затухания, логарифмического декремента затухания, а также соотношение (14), получаем
. Учитывая определения коэффициента затухания, логарифмического декремента затухания, а также соотношение (14), получаем
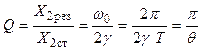 . (12.17)
. (12.17)
Можно показать, что в случае 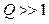 добротность можно выразить также через полуширину резонансной кривой, изображенной на рисунке 12.5:
добротность можно выразить также через полуширину резонансной кривой, изображенной на рисунке 12.5:
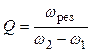 . (12.18)
. (12.18)
Экспериментальная часть
Описание экспериментальной установки
Исследование колебаний маятника проводится на установке, схема которой приведена на рисунке 12.6. Установка состоит из пружинного маятника, системы регистрации колебаний на основе пьезоэлектрического датчика, системы возбуждения вынужденных колебаний, а также системы обработки информации на персональном компьютере (ПК). Исследуемый пружинный маятник состоит из стальной пружины с коэффициентом жесткости 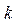 и тела маятника, в центре которого вмонтирован постоянный магнит. Движение маятника происходит в жидкости и при небольших скоростях колебаний возникающая сила трения может быть с достаточной точностью аппроксимирована линейным законом, т.е.
и тела маятника, в центре которого вмонтирован постоянный магнит. Движение маятника происходит в жидкости и при небольших скоростях колебаний возникающая сила трения может быть с достаточной точностью аппроксимирована линейным законом, т.е.
 .
.
Для регистрации колебаний используется пьезоэлектрический датчик, к которому подвешена пружина маятника. Во время движения маятника сила упругости пропорциональна смещению  .
.
Так как ЭДС, возникающая в пьезодатчике, в свою очередь пропорциональна силе давления, то сигнал, получаемый с датчика, будет пропорционален смещению тела маятника от положения равновесия.
Возбуждение колебаний осуществляется с помощью магнитного поля. Гармонический сигнал, создаваемый ПК, усиливается и подается на электромагнит, расположенный под телом маятника. В результате этого вокруг электромагнита переменное во времени и неоднородное в пространстве магнитное поле. Это поле действует на постоянный магнит, вмонтированный в тело маятника и создает внешнюю периодическую силу.
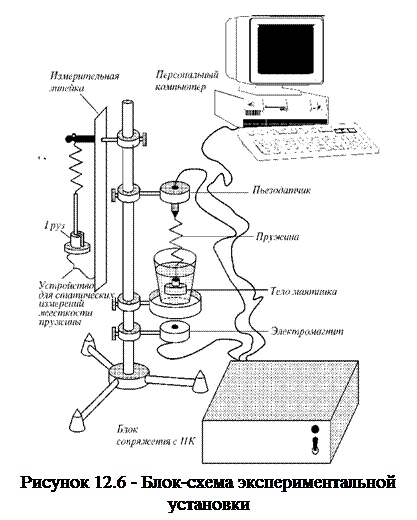
 |
Система обработки информации состоит из блока сопряжения с ПК (аналого-цифрового преобразователя) и персонального компьютера. Аналоговый сигнал с пьезоэлектрического датчика с помощью аналого-цифрового преобразователя представляется в цифровом виде и подается на ПК. Установка снабжена также устройством для статических измерений жесткости пружины. На исследуемую пружину могут подвешиваться грузы различной массы. Для регистрации растяжения пружины используется измерительная линейка.
Управление экспериментальной установкой с помощью ЭВМ
Рассмотрим возможные режимы работы программы: Статистика — этот пункт меню используется для обработки результатов первого… После набора данных нажимают на функциональную клавишу F2. На экране появляются рассчитанные с помощью метода…Проведение эксперимента
Измерения проводятся путем определения удлинения пружины под действием грузов с известными массами. Рекомендуется провести не менее 7–10 измерений… В ходе выполнения упражнения необходимо рассчитать значение собственной частоты колебаний маятникаОсновные итоги работы
В результате работы должны быть определены собственная частота колебаний пружинного маятника, декремент затухания и получены его амплитудно-частотная и фазо-частотная характеристики.
Контрольные вопросы
1 Что такое классический гармонический осциллятор?
2 Показать, что постоянная сила тяжести не влияет на частоту колебаний пружинного маятника.
3 На какой частоте происходят колебания пружинного маятника при наличии затухания?
4 На какой частоте происходят вынужденные колебания маятника?
5 Что такое коэффициент затухания, добротность?
6 На каких частотах наблюдаются резонансы смещения и скоростей?
Рекомендуемая литература
12.4.1 Зисман, Г.А. Курс общей физики: в 3 т. / Г.А. Зисман, О.М. Тодес. – СПб.: Лань, 2007. – Т.1: Механика. Молекулярная физика. Колебания и волны. – 340 с. - ISBN 978-5-8114-0753-8.
12.4.2 Иродов, И.Е. Механика. Основные законы механики / И.Е.Иродов. - М.: Бином, 2009. – 310 с. - ISBN 978-5-9963-0063-1.
12.4.3 Савельев, И.В. Курс общей физики: в 5 кн. / И.В.Савельев. – М.: АСТРЕЛЬ: АСТ, 2005. – Кн. 1: Механика. – 336 с. - ISBN 5-271-01034-1.
12.4.4 Сивухин, Д.В. Общий курс физики: в 3 т. / Д.В.Сивухин. - М.: Физматлит, 2002. – Т. 1: Механика. – 560 с. - ISBN 5-89155-078-4.
12.4.5 Трофимова, Т.И. Физика в таблицах и формулах / Т.И. Трофимова. – М.: Академия, 2006. – 448 с. - ISBN 5-7695-2277-1.
Приложение А
Расчет коэффициента затухания по ФЧХ
, (А.1) дифференцируя по частоте обе части (А.1) получаем:– Конец работы –
Используемые теги: Механика0.045
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: МЕХАНИКА
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов