И вывод расчетных формул
Машина Атвуда предназначена для исследования закона движения тел в поле земного тяготения. Устройство машины Атвуда изображено на рис. 2.1.

Рис. 2.1.
На верхнем конце шкалы 1 имеется легкий блок 2, вращающийся с небольшим трением, которое учитывается в работе. Через блок перекинута тонкая нить 3, на концах которой висят грузы А и В, имеющие равные массы m. Нить с грузами может удерживаться неподвижно электромагнитом 4. Выключение тока, текущего через электромагнит, при наличии перегрузка на грузе В приводит нить с грузами в движение. Для разрыва электрической цепи счетчика-секундомера служит приемный столик 5. При установке приемный столик следует располагать таким образом, чтобы верхняя плоскость дна его площадки находилась против нужного деления на шкале. Если системе, состоящей из трех тел – два груза А и В и блок, предоставить возможность двигаться, то грузы будут совершать поступательное движение, а блок – вращательное. Проследим за движением груза В, выбрав ось отсчета, направленную сверху вниз (рис. 2.2).
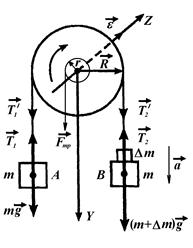
Рис. 2.2.
Двигаясь с ускорением а без начальной скорости, груз В за время t проходит по вертикали путь, который равен:
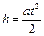 . (2.1)
. (2.1)
Из формулы (2.1) имеем:
 . (2.2)
. (2.2)
Скорость груза увеличивается со временем по закону u= at. В свою очередь, угол поворота радиуса блока изменяется со временем t по закону
 , (2.3)
, (2.3)
где e – угловое ускорение.
Угловая скорость к моменту времени t:
 . (2.4)
. (2.4)
Угловые скорость и ускорение связаны с линейной скоростью и тангенциальным ускорением точек блока, лежащих на его ободе на расстоянии R от оси вращения, следующими выражениями:
 и
и  .
.
Очевидно, что точки на ободе блока имеют ту же скорость и ускорение, что и груз В, т. е. uоб = u; at = a, поэтому
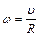 ; (2.5)
; (2.5)
 . (2.6)
. (2.6)
Угол поворота радиуса блока связан с числом его оборотов N выражением  Подставляя это значение j в формулу (2.3) и решая ее относительно N, получим:
Подставляя это значение j в формулу (2.3) и решая ее относительно N, получим:
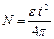 . (2.7)
. (2.7)
Ускорение a можно определить не только кинематически по зависимости (2.2), но и динамически. Для этого применим законы динамики поступательного и вращательного движений к движущейся системе. На каждый из движущихся грузов действуют силы: сила тяжести mg, направленная вниз, и сила натяжения нити Т, направленная вверх (рис. 2.2). Пусть масса перегрузка, лежащего на грузе В, равна Dm, а масса груза – m. Груз В вместе с перегрузком движется ускоренно вниз. Согласно второму закону Ньютона, имеем:
 .
.
Проектируя на ось системы отсчета у, получим:
 . (2.8)
. (2.8)
Применим второй закон Ньютона к грузу А. Если нить нерастяжима, то ускорение груза А равно ускорению груза В по абсолютной величине и противоположно по направлению. Его проекция на ось у равна –а. Поэтому по второму закону Ньютона
 . (2.9)
. (2.9)
Силы натяжения нити действуют не только на грузы, но и на блок. По третьему закону Ньютона силы  и
и  приложенные к ободу блока, равны соответственно Т1 и Т2 и противоположны им по направлению. При движении грузов блок ускоренно вращается по часовой стрелке. Следовательно,
приложенные к ободу блока, равны соответственно Т1 и Т2 и противоположны им по направлению. При движении грузов блок ускоренно вращается по часовой стрелке. Следовательно,  и силы натяжения нити по обе стороны блока будут различны. Поэтому для нахождения ускорения уравнения (2.8) и (2.9) должны быть еще уравнением моментов, определяющим закон вращательного движения блока.
и силы натяжения нити по обе стороны блока будут различны. Поэтому для нахождения ускорения уравнения (2.8) и (2.9) должны быть еще уравнением моментов, определяющим закон вращательного движения блока.
Момент сил, приложенных к блоку, складывается из момента сил натяжения нитей, равного произведению разности этих сил на плечо, равное радиусу блока, т. е.  , и момента сил трения Мтр.
, и момента сил трения Мтр.
Согласно основному закону динамики вращательного движения, вращающий момент, приложенный к блоку, равен произведению момента инерции I блока на его угловое ускорение e :
 . (2.10)
. (2.10)
Момент инерции блока равен:

Подставляя значение I в равенство (2.10) и решая совместно полученное выражение с уравнениями (2.8) и (2.9), получим:
 . (2.11)
. (2.11)
Так как
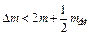 ,
,
то массой Δm в знаменателе формулы (2.11) можно пренебречь и записать:
 . (2.12)
. (2.12)
Выражение (2.12) показывает, что ускорение а линейно зависит от Δm, если R, m, mбл, Мтр остаются постоянными. Зависимость a = f(Δm) графически выражается прямой линией, которую можно построить по экспериментальным точкам, используя значения а, вычисленные из кинематических соображений по формуле (2.2).
Из формулы (2.12) следует, что при некотором значении массы перегрузка Δm0 система движется равномерно, т. е. а = 0.
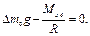
Отсюда находим момент сил трения:
Мтр = Δm0gR. (2.13)
Считая силу трения Fтр, приложенную к оси, постоянной, получим:
 , (2.14)
, (2.14)
где r – радиус оси.