рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Механика
- /
- Вид работы: Самостоятельные Работы
- /
- Лабораторная работа 3. ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАХОВОГО КОЛЕСА
Реферат Курсовая Конспект
Лабораторная работа 3. ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАХОВОГО КОЛЕСА
Лабораторная работа 3. ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАХОВОГО КОЛЕСА - Самостоятельная Работа, раздел Механика, Механика – это раздел физики, изучающий закономерности механического движения и причины, вызывающие или изменяющие это движение Цель Работы: Определить Момент Инерции Махового Колеса Динам...
Цель работы: определить момент инерции махового колеса динамическим методом.
Приборы и принадлежности: маховое колесо на одной оси со шкивом, секундомер, грузы, масштабная линейка.
Изучите теоретический материал по одному из учебных пособий [1, гл. I, § 5, гл. V, § 38, 39; 2, гл. I, § 1.5, гл. IV, § 4.1; 3, гл. III, § 10, 11; 4, гл. I, § 6, гл. IV, § 21, 22].
При изучении указанных пособий следует уяснить, что твердое тело можно представить как совокупность отдельных материальных точек, которые при вращательном движении тела описывают окружности. Центры этих окружностей находятся на оси вращения. Линейные скорость u и ускорение а точек, отстоящих от оси на разных расстояниях, будут неодинаковы. Угловые же скорость

и ускорение
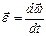
будут для всех точек твердого тела иметь одинаковые значения в данный момент времени. Обратите внимание на то, что угловая скорость в общем случае определяется как производная от углового перемещения j по времени, а угловое ускорение – как производная от угловой скорости по времени.
Полезно запомнить, что направление вектора угловой скорости  связано с направлением вращения тела правилом правого винта (буравчика).
связано с направлением вращения тела правилом правого винта (буравчика).
Для случая вращения некоторой точки (рис. 3.1) векторы угловой скорости  и углового ускорения
и углового ускорения 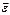 направлены перпендикулярно плоскости чертежа и проходят через центр вращения. При ускоренном вращении направления векторов
направлены перпендикулярно плоскости чертежа и проходят через центр вращения. При ускоренном вращении направления векторов  и
и 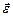 совпадают, при замедленном движении они направлены в противоположные стороны.
совпадают, при замедленном движении они направлены в противоположные стороны.

Рис. 3.1.
Между линейными и угловыми характеристиками движения существует зависимость, которая выражается следующими формулами:
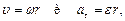
где  – тангенциальное ускорение.
– тангенциальное ускорение.
В динамике вращательного движения используются понятия момента инерции тела, момента силы. Момент инерции характеризует инертные свойства тела во вращательном движении, т. е. является мерой сопротивления тела к изменению его угловой скорости.
Момент инерции I материальной точки определяется выражением
 .
.
Он зависит как от массы m материальной точки, так и от расстояния r от точки до центра вращения.
Момент инерции тела относительно некоторой оси вращения определяется суммой моментов инерций отдельных материальных точек, на которые можно мысленно разбить тело:
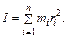
Момент инерции твердого тела при непрерывном распределении массы определяется выражением
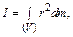
где интегрирование производится по всему объему тела.
При вращательном движении роль силы выполняет момент силы. Момент силы относительно точки О – это векторная величина, определяемая выражением
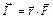 ,
,
где 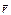 – радиус-вектор, соединяющий точку О и точку приложения
– радиус-вектор, соединяющий точку О и точку приложения
силы.
Направление вектора  определяется правилом правого винта (рис. 3.2).
определяется правилом правого винта (рис. 3.2).
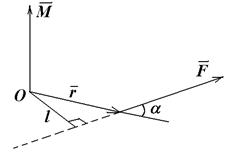
Рис. 3.2.
Модуль значения момента силы можно определить как
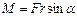 ,
,
где a – угол между вектором силы  и радиусом-вектором
и радиусом-вектором 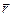 .
.
Величина  называется плечом силы и соответствует кратчайшему расстоянию от центра вращения до линии действия силы (рис. 3.2). Поэтому
называется плечом силы и соответствует кратчайшему расстоянию от центра вращения до линии действия силы (рис. 3.2). Поэтому
M = F∙l.
Основной закон динамики вращательного движения связывает момент силы, момент инерции и угловое ускорение тела и аналогичен второму закону Ньютона (основному закону динамики поступательного движения):
 ,
,
т. е. результирующий момент сил, действующих на тело относительно выбранной неподвижной оси, равен произведению момента инерции тела относительно той же оси на полученное телом угловое ускорение.
Вращающееся тело обладает кинетической энергией:
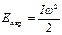
(сравните с формулой  для поступательного движения).
для поступательного движения).
В СИ единица измерения момента силы –  момента инерции –
момента инерции –

– Конец работы –
Эта тема принадлежит разделу:
Механика – это раздел физики, изучающий закономерности механического движения и причины, вызывающие или изменяющие это движение
ВВЕДЕНИЕ... Механика это раздел физики изучающий закономерности механического движения... Выполнение лабораторных работ по механике способствует развитию у студентов навыков самостоятельной работы и помогает...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Лабораторная работа 3. ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАХОВОГО КОЛЕСА
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов