Решение задач кинематики - раздел Механика, Теоретическая Механика Пример 3.
Даны Уравнения Движения Точки В Плоск...
Пример 3.
Даны уравнения движения точки в плоскости 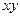 :
:
 ,
, 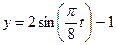
( ,
,  – в сантиметрах,
– в сантиметрах,  – в секундах).
– в секундах).
Определить: уравнение траектории точки; для момента времени  с найти скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
с найти скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Решение:
1. Для определения уравнения траектории точки исключим из заданных уравнений движения время 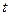 . Поскольку
. Поскольку 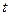 входит в аргументы тригонометрических функций, где один аргумент вдвое больше другого, используем формулу
входит в аргументы тригонометрических функций, где один аргумент вдвое больше другого, используем формулу
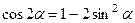 :
:
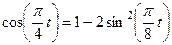 . (102)
. (102)
Из уравнений движения находим выражения соответствующих функций и подставляем в равенство (102). Получим

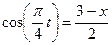 ,
,
 ,
,
следовательно,
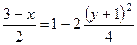 .
.
 Отсюда окончательно находим следующее уравнение траектории точки (параболы, рис. 41):
Отсюда окончательно находим следующее уравнение траектории точки (параболы, рис. 41):
 . (103)
. (103)
2. Скорость точки найдем по ее проекциям на координатные оси:
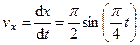 ,
, 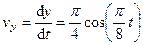 ,
,
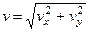 .
.
Для момента времени  с:
с: 
 ,
, 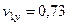
 ,
, 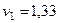
 . (104)
. (104)
3. Аналогично найдем ускорение точки:
 ,
,  ,
,
 .
.
Для момента времени  с:
с: 
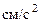 ,
, 
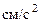 ,
, 
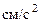 . (105)
. (105)
4. Касательное ускорение найдем, дифференцируя по времени равенство:

Получим
 ,
,
откуда
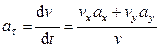 . (106)
. (106)
Числовые значения всех величин, входящих в правую часть (106), определены и даются в (104) и (105). Подставив в (106) эти числа, найдем сразу, что при  с:
с: 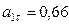
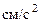 .
.
5. Нормальное ускорение точки 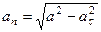 . Подставляя сюда найденные при
. Подставляя сюда найденные при  с числовые значения
с числовые значения  и
и 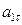 , получим, что
, получим, что 
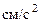 .
.
6. Радиус кривизны траектории 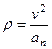 .
.
Подставляя сюда числовые значения  и
и 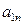 при
при  с, найдем, что
с, найдем, что 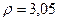 см.
см.
Ответ: 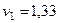
 ,
, 
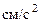 ,
, 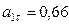
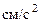 ,
, 
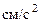 ,
, 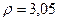 см.
см.
 Пример 4.
Пример 4. 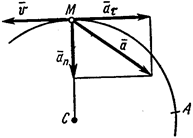 Точка движется по дуге окружности радиуса
Точка движется по дуге окружности радиуса 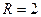 м по закону
м по закону  , (
, ( – в метрах,
– в метрах,  – в секундах), где
– в секундах), где  (рис. 42).
(рис. 42).
Определить: скорость и ускорение точки в момент времени  с.
с.
Решение:
Определяем скорость точки:
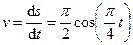 .
.
При  с получим
с получим 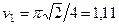
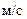 .
.
Ускорение находим по его касательной и нормальной составляющим:
 ,
,  ,
,  .
.
При  с получим
с получим 
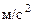 ,
, 
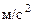 ,
, 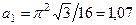
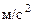 .
.
Изобразим на рис. 42 векторы  и
и  , учитывая знаки и считая положительным направление от
, учитывая знаки и считая положительным направление от 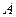 к
к 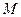 .
.
Ответ: 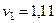
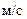 ,
, 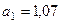
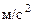 .
.
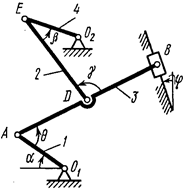 Пример 5. Механизм (рис. 43) состоит из стержней 1, 2, 3, 4 и ползуна
Пример 5. Механизм (рис. 43) состоит из стержней 1, 2, 3, 4 и ползуна  , соединенных друг с другом и с неподвижными опорами
, соединенных друг с другом и с неподвижными опорами  и
и  шарнирами.
шарнирами.

 Дано:
Дано:  ,
,  ,
,  ,
,  ,
, 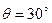 ,
, 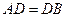 ,
, 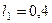 м,
м, 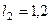 м,
м, 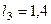 м,
м, 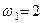 с-1,
с-1, 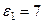 с-2 (направления
с-2 (направления  и
и  – против хода часовой стрелки).
– против хода часовой стрелки).
 Определить:
Определить:  ,
,  ,
, 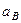 ,
,  ,
, 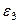 .
.
Решение:
1. Строим положение механизма в соответствии с заданными углами и выбранным масштабом длин (рис. 44; на этом рисунке изображаем все векторы скоростей).
 2. Определяем
2. Определяем  . Точка
. Точка  принадлежит стержню
принадлежит стержню  . Чтобы найти
. Чтобы найти  , надо знать скорость какой-нибудь другой точки этого стержня и направление
, надо знать скорость какой-нибудь другой точки этого стержня и направление 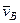 . По данным задачи, учитывая направление
. По данным задачи, учитывая направление 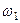 , можем определить
, можем определить  . Численно:
. Численно:
 м/с,
м/с,
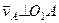 . (107)
. (107)
Направление 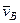 найдем, учтя, что точка
найдем, учтя, что точка  принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно. Теперь, зная
принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно. Теперь, зная  и направление
и направление 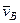 , воспользуемся теоремой о проекциях скоростей двух точек тела (стержня
, воспользуемся теоремой о проекциях скоростей двух точек тела (стержня  ) на прямую, соединяющую эти точки (прямая
) на прямую, соединяющую эти точки (прямая  ). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор
). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор 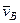 (проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим
(проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим
 ,
, 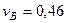 м/с. (108)
м/с. (108)
3. Определяем  . Точка
. Точка 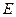 принадлежит стержню
принадлежит стержню  . Следовательно, по аналогии с предыдущим, чтобы определить
. Следовательно, по аналогии с предыдущим, чтобы определить  , надо сначала найти скорость точки
, надо сначала найти скорость точки  , принадлежащей одновременно стержню
, принадлежащей одновременно стержню  . Для этого, зная
. Для этого, зная  и
и 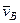 , строим мгновенный центр скоростей (МЦС) стержня
, строим мгновенный центр скоростей (МЦС) стержня  . Это точка
. Это точка 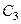 , лежащая на пересечении перпендикуляров к
, лежащая на пересечении перпендикуляров к  и
и 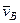 , восставленных из точек
, восставленных из точек 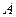 и
и  (к
(к  перпендикулярен стержень 1). По направлению вектора
перпендикулярен стержень 1). По направлению вектора  определяем направление поворота стержня
определяем направление поворота стержня  вокруг МЦС
вокруг МЦС 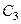 . Вектор
. Вектор  перпендикулярен отрезку
перпендикулярен отрезку  , соединяющему точки
, соединяющему точки  и
и 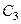 , и направлен в сторону поворота. Величину
, и направлен в сторону поворота. Величину  найдем из пропорции:
найдем из пропорции:
 . (109)
. (109)
Чтобы вычислить  и
и 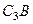 , заметим, что
, заметим, что  – прямоугольный, так как острые углы в нем равны 30° и 60°, и что
– прямоугольный, так как острые углы в нем равны 30° и 60°, и что  . Тогда
. Тогда  является равносторонним и
является равносторонним и  . В результате равенство (3) дает
. В результате равенство (3) дает
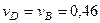 м/с,
м/с,  . (110)
. (110)
Так как точка 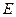 принадлежит одновременно стержню
принадлежит одновременно стержню  , вращающемуся вокруг
, вращающемуся вокруг  , то
, то 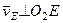 . Тогда, восставляя из точек
. Тогда, восставляя из точек 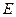 и
и  перпендикуляры к скоростям
перпендикуляры к скоростям  и
и  , построим МЦС
, построим МЦС 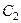 стержня
стержня  . По направлению вектора
. По направлению вектора  определяем направление поворота стержня
определяем направление поворота стержня  вокруг центра
вокруг центра 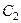 . Вектор
. Вектор  направлен в сторону поворота этого стержня. Из рис. 44 видно, что
направлен в сторону поворота этого стержня. Из рис. 44 видно, что 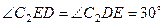 , откуда
, откуда  . Составив теперь пропорцию, найдем, что
. Составив теперь пропорцию, найдем, что
 ,
, 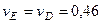 м/с. (110)
м/с. (110)
4. Определяем  . Так как МЦС стержня 2 известен (точка
. Так как МЦС стержня 2 известен (точка 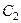 ) и
) и 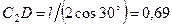 м, то
м, то
 с–1. (111)
с–1. (111)

 5. Определяем
5. Определяем  (рис. 45, на котором изображаем все векторы ускорений). Точка
(рис. 45, на котором изображаем все векторы ускорений). Точка  принадлежит стержню
принадлежит стержню  . Чтобы найти
. Чтобы найти  , надо знать ускорение какой-нибудь другой точки стержня
, надо знать ускорение какой-нибудь другой точки стержня  и траекторию точки
и траекторию точки  . По данным задачи можем определить
. По данным задачи можем определить  , где численно
, где численно
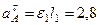 м/с2,
м/с2,
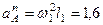 м/с2. (112)
м/с2. (112)
Вектор  направлен вдоль
направлен вдоль  , а
, а  – перпендикулярно
– перпендикулярно  . Изображаем эти векторы на чертеже (см. рис. 45). Так как точка
. Изображаем эти векторы на чертеже (см. рис. 45). Так как точка  одновременно принадлежит ползуну, то вектор
одновременно принадлежит ползуну, то вектор  параллелен направляющим ползуна. Изображаем вектор
параллелен направляющим ползуна. Изображаем вектор  на чертеже, полагая, что он направлен в ту же сторону, что и
на чертеже, полагая, что он направлен в ту же сторону, что и 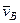 .
.
Для определения  воспользуемся равенством
воспользуемся равенством
 . (113)
. (113)
Изображаем на чертеже векторы 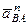 (вдоль
(вдоль 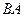 от
от  к
к 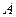 ) и
) и 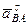 (в любую сторону перпендикулярно
(в любую сторону перпендикулярно 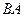 ). Численно
). Численно  Найдя
Найдя 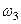 с помощью построенного МЦС
с помощью построенного МЦС 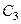 стержня 3, получим
стержня 3, получим
 с–1,
с–1, 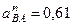 м/с2. (114)
м/с2. (114)
Таким образом, у величин, входящих в равенство (113), неизвестны только числовые значения  и
и 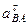 . Их можно найти, спроектировав обе части равенства (113) на какие-нибудь две оси.
. Их можно найти, спроектировав обе части равенства (113) на какие-нибудь две оси.
Чтобы определить  , спроектируем обе части равенства (113) на направление
, спроектируем обе части равенства (113) на направление 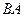 (ось
(ось  ). Тогда получим
). Тогда получим
 . (115)
. (115)
Подставив в равенство (10) числовые значения всех величин из (112) и (114), найдем, что
 м/с2. (116)
м/с2. (116)
Так как получилось  , то, следовательно, вектор
, то, следовательно, вектор  направлен как показано на рис. 45.
направлен как показано на рис. 45.
6. Определяем 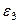 . Чтобы найти
. Чтобы найти 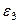 , сначала определим
, сначала определим 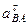 . Для этого обе части равенства (113) спроектируем на направление, перпендикулярное
. Для этого обе части равенства (113) спроектируем на направление, перпендикулярное  (ось
(ось 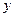 ). Тогда получим:
). Тогда получим:
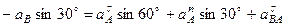 . (117)
. (117)
Подставив в равенство (12) числовые значения всех величин из (116) и (112), найдем, что  м/с2. Знак минус указывает, что направление
м/с2. Знак минус указывает, что направление 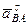 противоположно показанному на рис. 45.
противоположно показанному на рис. 45.
Теперь из равенства 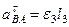 получим:
получим:
 с–2.
с–2.
Ответ: 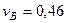 м/с,
м/с, 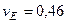 м/с,
м/с,  с–1,
с–1,  м/с2,
м/с2,  с–2.
с–2.

 Пример 6. Пластина
Пример 6. Пластина 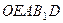 (
(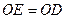 , рис. 46) вращается вокруг оси, проходящей через точку
, рис. 46) вращается вокруг оси, проходящей через точку 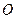 перпендикулярно плоскости пластины, по закону
перпендикулярно плоскости пластины, по закону  (положительное направление отсчета угла
(положительное направление отсчета угла  показано на рис. 46 дуговой стрелкой). По дуге окружности радиуса
показано на рис. 46 дуговой стрелкой). По дуге окружности радиуса 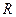 движется точка
движется точка  по закону
по закону  (положительное направление отсчета
(положительное направление отсчета  – от
– от 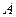 к
к  ).
).
Дано:  м,
м, 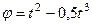 ,
,  (
( – в радианах,
– в радианах,  – в метрах,
– в метрах, 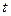 – в секундах).
– в секундах).
Определить: 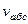 и
и 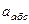 в момент времени
в момент времени  с.
с.
Решение:
Рассмотрим движение точки  как сложное, считая ее движение по дуге окружности относительным, а вращение пластины – переносным движением. Тогда абсолютная скорость
как сложное, считая ее движение по дуге окружности относительным, а вращение пластины – переносным движением. Тогда абсолютная скорость  и абсолютное ускорение
и абсолютное ускорение 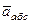 точки найдутся по формулам:
точки найдутся по формулам:
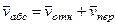 ,
, 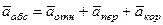 , (118)
, (118)
где, в свою очередь,
 ,
,  .
.
Определим все, входящие в равенства (118) величины.
1. Относительное движение. Это движение происходит по закону
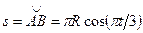 . (119)
. (119)
Сначала установим, где будет находиться точка  на дуге окружности в момент времени
на дуге окружности в момент времени 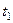 . Полагая в уравнении (119)
. Полагая в уравнении (119)  с, получим
с, получим
 .
.
Тогда
 .
.
Знак минус свидетельствует о том, что точка  в момент
в момент  с находится справа от точки
с находится справа от точки 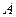 . Изображаем ее на рис. 46 в этом положении (точка
. Изображаем ее на рис. 46 в этом положении (точка  )).
)).
Теперь находим числовые значения 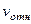 ,
,  и
и  :
:
 ,
,
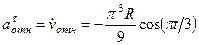 ,
,  ,
,
где 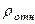 – радиус кривизны относительной траектории, равный радиусу окружности
– радиус кривизны относительной траектории, равный радиусу окружности 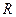 . Для момента
. Для момента  с, учитывая, что
с, учитывая, что  м, получим
м, получим
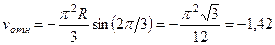 м/с,
м/с,
 м/с2,
м/с2,
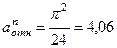 м/с2.
м/с2.
Знаки показывают, что вектор 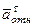 направлен в сторону положительного отсчета расстояния
направлен в сторону положительного отсчета расстояния  , а вектор
, а вектор 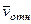 — в противоположную сторону; вектор
— в противоположную сторону; вектор  , направлен к центру
, направлен к центру  окружности. Изображаем все эти векторы на рис. 46.
окружности. Изображаем все эти векторы на рис. 46.
2. Переносное движение. Это движение (вращение) происходит по закону 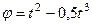 . Найдем сначала угловую скорость
. Найдем сначала угловую скорость 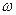 и угловое ускорение
и угловое ускорение  переносного вращения:
переносного вращения:
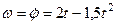 ,
, 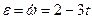
и при  с
с
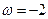 с–1 ,
с–1 ,  с–2. (120)
с–2. (120)
Знаки указывают, что в момент  с направления
с направления 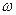 и
и  противоположны направлению положительного отсчета угла
противоположны направлению положительного отсчета угла  ; отметим это на рис. 46.
; отметим это на рис. 46.
Для определения 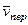 и
и 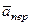 находим сначала расстояние
находим сначала расстояние  точки
точки  от оси вращения
от оси вращения 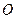 . Из рисунка видно, что
. Из рисунка видно, что 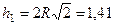 м. Тогда в момент времени
м. Тогда в момент времени  с, учитывая равенства (4), получим
с, учитывая равенства (4), получим
 м/с,
м/с,
 м/с2,
м/с2,
 м/с2. (121)
м/с2. (121)
Изображаем на рис. 46 векторы 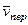 и
и  с учетом направлений
с учетом направлений 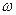 и
и  и вектор
и вектор  (направлен к оси вращения).
(направлен к оси вращения).
3. Кориолисово ускорение. Модуль кориолисова ускорения определяем по формуле
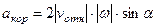 ,
,
где  – угол между вектором
– угол между вектором 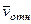 и осью вращения (вектором
и осью вращения (вектором 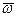 ). В нашем случае этот угол равен 90°, так как ось вращения перпендикулярна плоскости пластины, в которой расположен вектор
). В нашем случае этот угол равен 90°, так как ось вращения перпендикулярна плоскости пластины, в которой расположен вектор 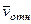 . Численно в момент времени
. Численно в момент времени  с, так как в этот момент
с, так как в этот момент  м/с,
м/с, 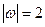 с–1, получим
с–1, получим
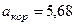 м/с2. (122)
м/с2. (122)
Направление 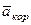 найдем по правилу Н.Е. Жуковского: так как вектор
найдем по правилу Н.Е. Жуковского: так как вектор 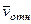 лежит в плоскости, перпендикулярной оси вращения, то повернем его на 90° в направлении
лежит в плоскости, перпендикулярной оси вращения, то повернем его на 90° в направлении 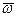 , т.е. по ходу часовой стрелки. Изображаем
, т.е. по ходу часовой стрелки. Изображаем 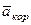 на рис. 46. (Иначе направление
на рис. 46. (Иначе направление 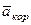 можно найти, учтя, что
можно найти, учтя, что 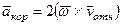 .)
.)
Таким образом, значения всех входящих в правые части равенств (118) векторов найдены и для определения  и
и 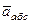 остается только сложить эти векторы. Произведем это сложение аналитически.
остается только сложить эти векторы. Произведем это сложение аналитически.
4. Абсолютная скорость. Проведем координатные оси 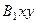 (см. рис. 46) и спроектируем почленно обе части равенства
(см. рис. 46) и спроектируем почленно обе части равенства 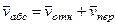 на эти оси. Получим для момента времени
на эти оси. Получим для момента времени  с:
с:
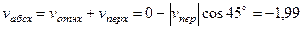 м/с,
м/с,
 м/с.
м/с.
После этого находим
 м/с.
м/с.
Учитывая, что в данном случае угол между 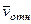 и
и 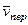 равен 45°, значение
равен 45°, значение 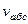 можно еще определить по формуле
можно еще определить по формуле
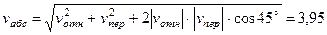 м/с.
м/с.
5. Абсолютное ускорение. По теореме о сложении ускорений
 . (123)
. (123)
Для определения 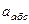 спроектируем обе части равенства (7) на проведенные оси
спроектируем обе части равенства (7) на проведенные оси  . Получим для момента времени
. Получим для момента времени  с:
с:
 м/с2,
м/с2,
 м/с2,
м/с2,
После этого находим
 м/с2.
м/с2.
Ответ:  м/с,
м/с,  м/с2.
м/с2.
Все темы данного раздела:
Алгебраический момент силы относительно точки
Алгебраическим моментом силыотносительно точки называют произведение модуля силы на плечо силы относите
Векторный момент силы относительно точки
Векторным моментом с
Момент силы относительно оси
Моментом силы относительно оси называют алгебраический момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью (рис. 4). Момент сил
Пара сил и алгебраический момент пары сил
Парой сил называют систему двух равных по модулю параллельных сил, направленных в противоположные стороны
Аксиомы статики
При формулировке аксиом предполагаем, что на твердое тело или материальную точку действуют силы, которые указаны в соответствующей аксиоме.
I. Аксиома о равновесии системы двух сил
Простейшие теоремы статики
Теорема о переносе силы вдоль линии действия: Действие силы на твердое тело не изменится от переноса
Теорема о трех силах: если твердое тело под действием трех сил
Приведение системы сил к простейшей системе. Условия равновесия
Лемма о параллельном переносе сил: силу можно переносить параллельно самой себе в любую точку твердого тела, добавляя при этом пару сил, векторный момент которой равен векторному моменту
Равновесие пар сил
Если на твердое тело действуют пары сил, как угодно расположенные в пространстве, то эти пары сил можно заменить одной эквивалентной парой сил, векторный момент которой равен сумме векторных момент
Условия равновесия произвольной системы сил в векторной форме
Векторные условия равновесия произвольной системы сил: для равновесия системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы главный вектор системы сил был равен нулю и главный
Условия равновесия пространственной системы сходящихся сил
Для равновесия пространственной системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы проекций сил на каждую из трех прямоугольных осей координат были равны н
Условия равновесия плоской системы сил
Расположим оси и в плос
Центр параллельных сил
Пусть на тело действует система параллельных сил . Такая система имеет равнодействующую
Способы нахождения центра тяжести
Симметричные тела. Если тело имеет плоскость (ось, центр) симметрии, то его центр тяжести находится в этой плоскости (на оси, в центре).
Распределенные силы
В статике рассматривают силы, приложенные к твердому телу в какой-либо его точке, и поэтому такие силы называют сосредоточенными. В действительности обычно силы бывают приложены к какой-либо
Трение скольжения
При движении или стремлении двигать одно тело по поверхности другого в касательной плоскости поверхностей соприкосновения возникает сила трения скольжения (трение первого рода).
Пус
Трение качения
Если одно тело, например цилиндрический каток, катить или стремиться катить по поверхности другого тела, то кроме силы трения скольжения из-за деформации поверхностей тел дополнительно возникает па
Решение задач статики
Пример 1.На угольник (
Кинематика точки
В кинематике точки рассматриваются характеристики движения точки, такие, как скорость, ускорение, и методы их определения при различных способах задания движения. Важным в кинематике точки является
Скорость и ускорение точки
Одной из основных характеристик движения точки является ее скорость относительно выбранной системы отсчета, ко
Частные случаи движения точки
Равномерное движение. При равномерном движении точки по траектории любой формы , следовательно, постоян
Кинематика твердого тела
Числом степеней свободы твердого тела называют число независимых параметров, определяющих положение тела относительно рассматриваемой системы отсчета.
Движение твердого тела во мног
Поступательное движение твердого тела
Поступательным движением твердого тела называют такое его движение, при котором любая прямая, жестко скрепленная с телом, остается параллельной своему первоначальному положению в каждый моме
Вращение твердого тела вокруг неподвижной оси
Вращением твердого тела вокруг неподвижной оси (оси вращения) называется такое его движение, при котором точки тела, лежащие на оси вращения, остаются неподвижными в течение всего времени дв
Частные случаи вращения твердого тела
Вращение называется равномерным, если . Алгебраическая угловая скорость отличается от модуля угловой ск
Скорости и ускорения точек тела при вращении вокруг неподвижной оси
Известно уравнение вращения твердого тела вокруг неподвижной оси (рис. 29). Расстояние
Векторы угловой скорости и углового ускорения
Введем понятия векторов угловой скорости и углового ускорения тела. Если – единичный вектор оси вращения, напр
Векторные формулы для скоростей и ускорений точек тела
Выразим скорость, касательное, нормальное и полное ускорения точки тела в векторной форме (рис. 32). Скорость точки по модулю и направлению можно представить векторным произведением
Сложное движение точки
Для изучения некоторых, более сложных видов движений твердого тела целесообразно рассмотреть простейшее сложное движение точки. Во многих задачах движение точки приходится рассматривать относительн
Ускорение Кориолиса
Рассмотрим ускорение Кориолиса и его свойства. Оно определяется формулой (81)
.
Угловую ско
Плоское (плоскопараллельное) движение твердого тела
Плоским движением твердого тела называют такое его движение, при котором каждая его точка все время движется в одной и той же плоскости. Плоскости, в которых движутся отдельные точки, паралл
Скорости точек плоской фигуры
Применяя к плоскому движению теорему о сложении скоростей для какой-либо точки фигуры, получаем
Мгновенный центр скоростей
В каждый момент вр
Ускорения точек плоской фигуры
Рассматривая плоское движение плоской фигуры как сложное, состоящее из переносного поступательного вместе с полюсом
Мгновенный центр ускорений
В каждый момент движения плоской фигуры в своей плоскости, если и
Аксиомы динамики
I. Первая аксиома (законом классической механики, закон инерции): материальная точка, на которую не действуют силы или действует равновесная система сил, обладает способност
Дифференциальные уравнения движения материальной точки
Используя основной закон динамики, можно получить дифференциальные уравнения движения материальной точки в различных системах координат. По аксиоме о связях и силах реакций связей можно получить ди
Первая задача
Зная массу точки и ее закон движения, можно найти действующую на точку силу. Действительно, если, например, заданы уравнения движения точки в декартовой системе координат
Вторая задача
По заданной массе и действующей на точку силе необходимо определить движение этой точки. Рассмотрим решение этой задачи в прямоугольной декартовой системе координат. В общем случае сила
Дифференциальные уравнения относительного движения материальной точки
Имеем инерциальную систему отсчета и материальную точку массой
Центр масс
При рассмотрении движения твердых тел и других механических систем важное значение имеет точка, называемая центром масс. Если механическая система состоит
Моменты инерции относительно точки и оси
Моментом инерции механической системы, состоящей из
Теорема Штейнера
Установим зависимость
Однородный стержень
Имеем однородный стержень длиной и массой
Прямоугольная пластина
Прямоугольная тонкая пластина имеет размеры и
Сплошной диск
Имеем тонкий однородный диск радиусом и массой
Тонкое кольцо (круглое колесо)
Имеем тонкое кольцо радиусом и массой
Круглый цилиндр
Для круглого однородного цилиндра, масса которого , радиус
Теоремы динамики
Внешними силами механической системы называются силы, с которыми действуют на точки системы тела и точки, не входящие в рассматриваемую систему.
Внутренними силами механическ
Теорема о движении центра масс
Центр масс системы движется так же, как и материальная точка, масса которой равна массе всей системы, если на точку действуют все внешние силы, приложенные к механической системе:
Количество движения точки и системы
Количеством движения материальной точки называют вектор, равный произведению массы точки
Теорема об изменении количества движения точки
Теорема об изменении количества движения точки в дифференциальной форме: первая производная по времени от количества движения точки равна действующей на точку силе:
Теорема об изменении количества движения системы
Теорема об изменении количества движения системы в дифференциальной форме: производная по времени от количества движения системы равна векторной сумме всех внешних сил, действующих на сис
Законы сохранения количества движения
Законы сохранения количества движения системы получаются как частные случаи теоремы об изменении количества движения для системы в зависимости от особенностей системы внешних сил, приложенных к рас
Теорема об изменении кинетического момента
Для материальной точки массой , движущейся со скоростью
Теорема об изменении кинетического момента точки
Первая производная по времени от кинетического момента точки относительно какого-либо центра равна моменту силы относительно того же центра:
Теорема об изменении кинетического момента системы
Первая производная по времени от кинетического момента системы относительно какой-либо точки равна векторной сумме моментов внешних сил, действующих на систему, относительно той же точки.
Законы сохранения кинетических моментов
1. Если главный момент внешних сил системы относительно точки равен нулю, т. е.
Дифференциальное уравнение вращения твердого тела вокруг неподвижной оси
Из теоремы об изменении кинетического момента (172') следует дифференциальное уравнение вращения твердого тела вокруг неподвижной оси
Теорема об изменении кинетического момента системы в относительном движении по отношению к центру масс
Пусть механическая система совершает движение относительно основной системы координат . Возьмем подвижную сист
Дифференциальные уравнения плоского движения твердого тела
Для твердого тела, совершающего плоское движение и, следовательно, имеющего три степени свободы, соответственно получим следующие три дифференциальных уравнения:
Работа силы
Работа силы на каком-либо перемещении является одной из основных характеристик, оценивающих действие силы на этом перемещении.
Кинетическая энергия
Кинетическая энергия точки и системы. Кинетической энергией материальной точки называют половину произведения массы точки на квадрат ее скорости, т.е.
Теорема об изменении кинетической энергии точки
Теорема об изменении кинетической энергии точки в дифференциальной форме: дифференциал кинетической энергии точки равен элементарной работе силы, действующей на точку.
Теорема об изменении кинетической энергии системы
Теорема об изменении кинетической энергии системы в дифференциальной форме: дифференциал от кинетической энергии системы равен сумме элементарных работ всех внешних и внутренних си
Принцип Даламбера для материальной точки
Принцип Даламбера для свободной материальной точки эквивалентен основному закону динамики. Для несвободной точки он эквивалентен основному закону вместе с аксиомой связей.
Уравнение движен
Принцип Даламбера для системы материальных точек
Рассмотрим систему материальных точек. К каждой точке системы в общем случае приложены равнодействующая актив
Силы инерции твердого тела в частных случаях его движения
При поступательном движении. Если твердое тело движется поступательно, то ускорения его точек одинаковы. Силы инерции этих точек составляют систему параллельных сил, направленных в од
Возможные перемещения
Для одной точки возможным (виртуальным) перемещением называется такое бесконечно милое (элементарное) мысленное перемещение, которое допускается в рассматриваемый момент времени наложенными на т
Элементарная работа силы на возможном перемещении. Идеальные связи
Элементарную работу силы на возможном перемещении ее точки приложения вычисляют по обычным формулам для элементарной работы, т.е.
Принцип возможных перемещений
Принцип возможных перемещений, или принцип Лагранжа, содержит необходимые и достаточные условия равновесия некоторых механических систем. Он формулируется следующим образом: для ра
Обобщенные координаты системы
Пусть система состоит из точек и, следовательно, ее положение в пространстве в каждый момент времени определя
Обобщенные силы
Запишем сумму элементарных работ сил, действующих на точки системы, на возможном перемещении системы:
Вычисление обобщенной силы
1. Обобщенную силу можно вычислить по формуле (227), ее определяющей, т.е.
.
2. Обобщенные
Общее уравнение динамики
Общее уравнение динамики для системы с любыми связями (объединенный принцип Даламбера-Лагранжа или общее уравнение механики):
Уравнения Лагранжа второго рода
Уравнения Лагранжа можно рассматривать как алгоритм получения дифференциальных уравнений движения системы, т.е. дифференциальных уравнений относительно обобщенных координат.
Уравнения Лагр
Решение задач динамики
Пример 7. На вертикальном участке
Библиографический список
1. Никитин Н.Н. Курс теоретической механики: учебник для машиностроит. и приборостроит. спец. вузов / Н.Н. Никитин. – М.: Высш. шк., 1990. 607с.
2. Бутенин Н.В. Курс теоретической механики
 :
: ,
, 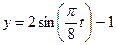
 ,
, 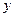 – в сантиметрах,
– в сантиметрах, 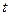 – в секундах).
– в секундах). с найти скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
с найти скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.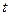 . Поскольку
. Поскольку 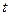 входит в аргументы тригонометрических функций, где один аргумент вдвое больше другого, используем формулу
входит в аргументы тригонометрических функций, где один аргумент вдвое больше другого, используем формулу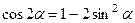 :
: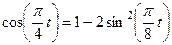 . (102)
. (102)
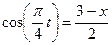 ,
, ,
,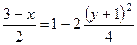 .
. Отсюда окончательно находим следующее уравнение траектории точки (параболы, рис. 41):
Отсюда окончательно находим следующее уравнение траектории точки (параболы, рис. 41): . (103)
. (103)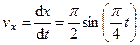 ,
, 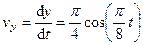 ,
,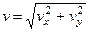 .
. с:
с: 
 ,
, 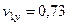
 ,
, 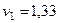
 . (104)
. (104) ,
,  ,
, .
. с:
с: 
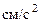 ,
, 
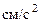 ,
, 
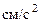 . (105)
. (105)
 ,
,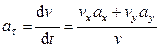 . (106)
. (106) с:
с: 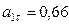
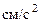 .
.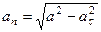 . Подставляя сюда найденные при
. Подставляя сюда найденные при  с числовые значения
с числовые значения  и
и 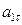 , получим, что
, получим, что 
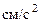 .
.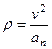 .
. и
и 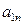 при
при  с, найдем, что
с, найдем, что 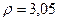 см.
см.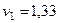
 ,
, 
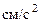 ,
, 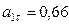
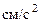 ,
, 
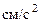 ,
, 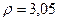 см.
см. Пример 4.
Пример 4.  Точка движется по дуге окружности радиуса
Точка движется по дуге окружности радиуса 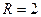 м по закону
м по закону  , (
, ( – в метрах,
– в метрах, 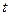 – в секундах), где
– в секундах), где  (рис. 42).
(рис. 42). с.
с.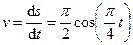 .
. с получим
с получим 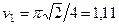
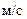 .
. ,
,  ,
,  .
. с получим
с получим 
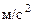 ,
, 
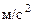 ,
, 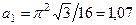
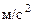 .
. и
и  , учитывая знаки и считая положительным направление от
, учитывая знаки и считая положительным направление от 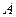 к
к 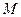 .
.
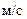 ,
, 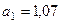
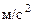 .
. Пример 5. Механизм (рис. 43) состоит из стержней 1, 2, 3, 4 и ползуна
Пример 5. Механизм (рис. 43) состоит из стержней 1, 2, 3, 4 и ползуна  , соединенных друг с другом и с неподвижными опорами
, соединенных друг с другом и с неподвижными опорами  и
и  шарнирами.
шарнирами.
 Дано:
Дано:  ,
,  ,
,  ,
,  ,
, 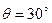 ,
, 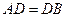 ,
, 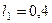 м,
м, 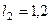 м,
м, 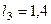 м,
м, 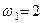 с-1,
с-1, 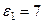 с-2 (направления
с-2 (направления  и
и  – против хода часовой стрелки).
– против хода часовой стрелки). Определить:
Определить:  ,
,  ,
, 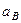 ,
,  ,
, 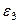 .
. 2. Определяем
2. Определяем  . Точка
. Точка  принадлежит стержню
принадлежит стержню  . Чтобы найти
. Чтобы найти  , надо знать скорость какой-нибудь другой точки этого стержня и направление
, надо знать скорость какой-нибудь другой точки этого стержня и направление 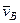 . По данным задачи, учитывая направление
. По данным задачи, учитывая направление 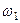 , можем определить
, можем определить  . Численно:
. Численно: м/с,
м/с,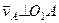 . (107)
. (107)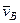 найдем, учтя, что точка
найдем, учтя, что точка  принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно. Теперь, зная
принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно. Теперь, зная  и направление
и направление 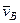 , воспользуемся теоремой о проекциях скоростей двух точек тела (стержня
, воспользуемся теоремой о проекциях скоростей двух точек тела (стержня  ) на прямую, соединяющую эти точки (прямая
) на прямую, соединяющую эти точки (прямая  ). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор
). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор 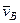 (проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим
(проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим ,
, 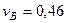 м/с. (108)
м/с. (108) . Точка
. Точка 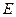 принадлежит стержню
принадлежит стержню  . Следовательно, по аналогии с предыдущим, чтобы определить
. Следовательно, по аналогии с предыдущим, чтобы определить  , надо сначала найти скорость точки
, надо сначала найти скорость точки  , принадлежащей одновременно стержню
, принадлежащей одновременно стержню  . Для этого, зная
. Для этого, зная  и
и 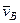 , строим мгновенный центр скоростей (МЦС) стержня
, строим мгновенный центр скоростей (МЦС) стержня  . Это точка
. Это точка 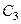 , лежащая на пересечении перпендикуляров к
, лежащая на пересечении перпендикуляров к  и
и 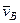 , восставленных из точек
, восставленных из точек 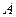 и
и  (к
(к  перпендикулярен стержень 1). По направлению вектора
перпендикулярен стержень 1). По направлению вектора  определяем направление поворота стержня
определяем направление поворота стержня  вокруг МЦС
вокруг МЦС 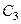 . Вектор
. Вектор  перпендикулярен отрезку
перпендикулярен отрезку  , соединяющему точки
, соединяющему точки  и
и 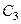 , и направлен в сторону поворота. Величину
, и направлен в сторону поворота. Величину  найдем из пропорции:
найдем из пропорции: . (109)
. (109) и
и 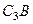 , заметим, что
, заметим, что  – прямоугольный, так как острые углы в нем равны 30° и 60°, и что
– прямоугольный, так как острые углы в нем равны 30° и 60°, и что  . Тогда
. Тогда  является равносторонним и
является равносторонним и  . В результате равенство (3) дает
. В результате равенство (3) дает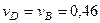 м/с,
м/с,  . (110)
. (110)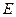 принадлежит одновременно стержню
принадлежит одновременно стержню  , вращающемуся вокруг
, вращающемуся вокруг  , то
, то 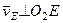 . Тогда, восставляя из точек
. Тогда, восставляя из точек 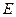 и
и  перпендикуляры к скоростям
перпендикуляры к скоростям  и
и  , построим МЦС
, построим МЦС 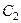 стержня
стержня  . По направлению вектора
. По направлению вектора  определяем направление поворота стержня
определяем направление поворота стержня  вокруг центра
вокруг центра 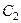 . Вектор
. Вектор  направлен в сторону поворота этого стержня. Из рис. 44 видно, что
направлен в сторону поворота этого стержня. Из рис. 44 видно, что 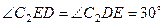 , откуда
, откуда  . Составив теперь пропорцию, найдем, что
. Составив теперь пропорцию, найдем, что ,
, 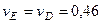 м/с. (110)
м/с. (110) . Так как МЦС стержня 2 известен (точка
. Так как МЦС стержня 2 известен (точка 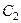 ) и
) и 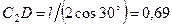 м, то
м, то с–1. (111)
с–1. (111)
 5. Определяем
5. Определяем  (рис. 45, на котором изображаем все векторы ускорений). Точка
(рис. 45, на котором изображаем все векторы ускорений). Точка  принадлежит стержню
принадлежит стержню  . Чтобы найти
. Чтобы найти  , надо знать ускорение какой-нибудь другой точки стержня
, надо знать ускорение какой-нибудь другой точки стержня  и траекторию точки
и траекторию точки  . По данным задачи можем определить
. По данным задачи можем определить  , где численно
, где численно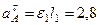 м/с2,
м/с2,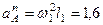 м/с2. (112)
м/с2. (112) направлен вдоль
направлен вдоль  , а
, а  – перпендикулярно
– перпендикулярно  . Изображаем эти векторы на чертеже (см. рис. 45). Так как точка
. Изображаем эти векторы на чертеже (см. рис. 45). Так как точка  одновременно принадлежит ползуну, то вектор
одновременно принадлежит ползуну, то вектор  параллелен направляющим ползуна. Изображаем вектор
параллелен направляющим ползуна. Изображаем вектор  на чертеже, полагая, что он направлен в ту же сторону, что и
на чертеже, полагая, что он направлен в ту же сторону, что и 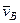 .
. воспользуемся равенством
воспользуемся равенством . (113)
. (113)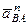 (вдоль
(вдоль 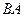 от
от  к
к 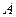 ) и
) и 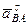 (в любую сторону перпендикулярно
(в любую сторону перпендикулярно 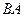 ). Численно
). Численно  Найдя
Найдя 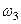 с помощью построенного МЦС
с помощью построенного МЦС 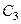 стержня 3, получим
стержня 3, получим с–1,
с–1, 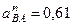 м/с2. (114)
м/с2. (114) и
и 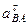 . Их можно найти, спроектировав обе части равенства (113) на какие-нибудь две оси.
. Их можно найти, спроектировав обе части равенства (113) на какие-нибудь две оси. , спроектируем обе части равенства (113) на направление
, спроектируем обе части равенства (113) на направление 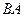 (ось
(ось  ). Тогда получим
). Тогда получим . (115)
. (115) м/с2. (116)
м/с2. (116) , то, следовательно, вектор
, то, следовательно, вектор  направлен как показано на рис. 45.
направлен как показано на рис. 45.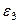 . Чтобы найти
. Чтобы найти 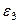 , сначала определим
, сначала определим 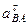 . Для этого обе части равенства (113) спроектируем на направление, перпендикулярное
. Для этого обе части равенства (113) спроектируем на направление, перпендикулярное  (ось
(ось 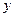 ). Тогда получим:
). Тогда получим: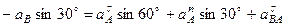 . (117)
. (117) м/с2. Знак минус указывает, что направление
м/с2. Знак минус указывает, что направление 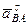 противоположно показанному на рис. 45.
противоположно показанному на рис. 45.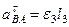 получим:
получим: с–2.
с–2.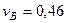 м/с,
м/с, 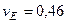 м/с,
м/с,  с–1,
с–1,  м/с2,
м/с2,  с–2.
с–2.
 Пример 6. Пластина
Пример 6. Пластина 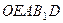 (
(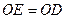 , рис. 46) вращается вокруг оси, проходящей через точку
, рис. 46) вращается вокруг оси, проходящей через точку 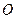 перпендикулярно плоскости пластины, по закону
перпендикулярно плоскости пластины, по закону  (положительное направление отсчета угла
(положительное направление отсчета угла  показано на рис. 46 дуговой стрелкой). По дуге окружности радиуса
показано на рис. 46 дуговой стрелкой). По дуге окружности радиуса 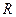 движется точка
движется точка  по закону
по закону  (положительное направление отсчета
(положительное направление отсчета  – от
– от 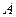 к
к  ).
). м,
м, 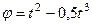 ,
,  (
( – в радианах,
– в радианах,  – в метрах,
– в метрах, 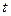 – в секундах).
– в секундах).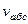 и
и 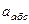 в момент времени
в момент времени  с.
с. как сложное, считая ее движение по дуге окружности относительным, а вращение пластины – переносным движением. Тогда абсолютная скорость
как сложное, считая ее движение по дуге окружности относительным, а вращение пластины – переносным движением. Тогда абсолютная скорость  и абсолютное ускорение
и абсолютное ускорение 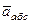 точки найдутся по формулам:
точки найдутся по формулам: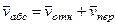 ,
, 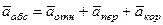 , (118)
, (118) ,
,  .
.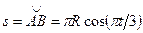 . (119)
. (119) на дуге окружности в момент времени
на дуге окружности в момент времени 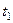 . Полагая в уравнении (119)
. Полагая в уравнении (119)  с, получим
с, получим .
. .
. в момент
в момент  с находится справа от точки
с находится справа от точки 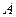 . Изображаем ее на рис. 46 в этом положении (точка
. Изображаем ее на рис. 46 в этом положении (точка  )).
)).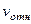 ,
,  и
и  :
: ,
,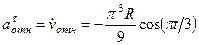 ,
,  ,
,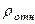 – радиус кривизны относительной траектории, равный радиусу окружности
– радиус кривизны относительной траектории, равный радиусу окружности 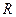 . Для момента
. Для момента  с, учитывая, что
с, учитывая, что  м, получим
м, получим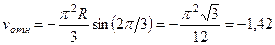 м/с,
м/с, м/с2,
м/с2,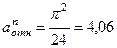 м/с2.
м/с2.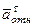 направлен в сторону положительного отсчета расстояния
направлен в сторону положительного отсчета расстояния  , а вектор
, а вектор 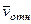 — в противоположную сторону; вектор
— в противоположную сторону; вектор  , направлен к центру
, направлен к центру  окружности. Изображаем все эти векторы на рис. 46.
окружности. Изображаем все эти векторы на рис. 46.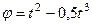 . Найдем сначала угловую скорость
. Найдем сначала угловую скорость 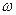 и угловое ускорение
и угловое ускорение  переносного вращения:
переносного вращения: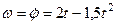 ,
, 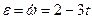
 с
с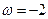 с–1 ,
с–1 ,  с–2. (120)
с–2. (120) с направления
с направления 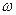 и
и  противоположны направлению положительного отсчета угла
противоположны направлению положительного отсчета угла  ; отметим это на рис. 46.
; отметим это на рис. 46.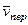 и
и 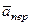 находим сначала расстояние
находим сначала расстояние  точки
точки  от оси вращения
от оси вращения 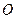 . Из рисунка видно, что
. Из рисунка видно, что 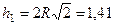 м. Тогда в момент времени
м. Тогда в момент времени  с, учитывая равенства (4), получим
с, учитывая равенства (4), получим м/с,
м/с, м/с2,
м/с2, м/с2. (121)
м/с2. (121)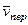 и
и  с учетом направлений
с учетом направлений 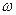 и
и  и вектор
и вектор  (направлен к оси вращения).
(направлен к оси вращения).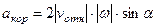 ,
, – угол между вектором
– угол между вектором 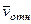 и осью вращения (вектором
и осью вращения (вектором 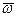 ). В нашем случае этот угол равен 90°, так как ось вращения перпендикулярна плоскости пластины, в которой расположен вектор
). В нашем случае этот угол равен 90°, так как ось вращения перпендикулярна плоскости пластины, в которой расположен вектор 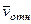 . Численно в момент времени
. Численно в момент времени  с, так как в этот момент
с, так как в этот момент  м/с,
м/с, 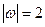 с–1, получим
с–1, получим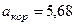 м/с2. (122)
м/с2. (122)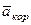 найдем по правилу Н.Е. Жуковского: так как вектор
найдем по правилу Н.Е. Жуковского: так как вектор 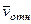 лежит в плоскости, перпендикулярной оси вращения, то повернем его на 90° в направлении
лежит в плоскости, перпендикулярной оси вращения, то повернем его на 90° в направлении 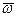 , т.е. по ходу часовой стрелки. Изображаем
, т.е. по ходу часовой стрелки. Изображаем 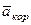 на рис. 46. (Иначе направление
на рис. 46. (Иначе направление 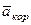 можно найти, учтя, что
можно найти, учтя, что 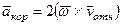 .)
.) и
и 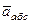 остается только сложить эти векторы. Произведем это сложение аналитически.
остается только сложить эти векторы. Произведем это сложение аналитически.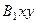 (см. рис. 46) и спроектируем почленно обе части равенства
(см. рис. 46) и спроектируем почленно обе части равенства 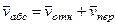 на эти оси. Получим для момента времени
на эти оси. Получим для момента времени  с:
с: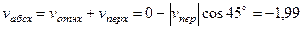 м/с,
м/с, м/с.
м/с. м/с.
м/с.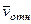 и
и 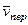 равен 45°, значение
равен 45°, значение 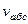 можно еще определить по формуле
можно еще определить по формуле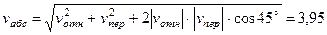 м/с.
м/с. . (123)
. (123) спроектируем обе части равенства (7) на проведенные оси
спроектируем обе части равенства (7) на проведенные оси  . Получим для момента времени
. Получим для момента времени  с:
с: м/с2,
м/с2, м/с2,
м/с2, м/с2.
м/с2. м/с,
м/с,  м/с2.
м/с2.






Новости и инфо для студентов