Преобразования Лоренца - раздел Механика, Физика будет изучаться в течение 4-х семестров: в первом: – физические основы классической и релятивистской механики Постулаты Эйнштейна Требовали Коренного Пересмотра Представлений О Свойствах ...
Постулаты Эйнштейна требовали коренного пересмотра представлений о свойствах пространства, времени и движения. Покажем это на простом примере.
Представим себе, что движущейся системой отсчета K', является поезд. Пусть в момент, когда его хвостовой вагон поравнялся со стрелочником (система отсчета K), стоящим на насыпи, из этого вагона был послан световой сигнал машинисту. Через время  машинист этот сигнал регистрирует, тогда скорость света
машинист этот сигнал регистрирует, тогда скорость света  , где
, где  – длина поезда в системе K'.
– длина поезда в системе K'.
Обозначим через  время, отсчитываемое стрелочником. Что касается пути, пройденного светом с точки зрения стрелочника, то он состоит из длины поезда
время, отсчитываемое стрелочником. Что касается пути, пройденного светом с точки зрения стрелочника, то он состоит из длины поезда  , движущегося со скоростью V, и расстояния Vdt, на которое за время
, движущегося со скоростью V, и расстояния Vdt, на которое за время  хвостовой вагон отъедет от стрелочника.
хвостовой вагон отъедет от стрелочника.
Итак, с точки зрения стрелочника  .
.
Очевидно, что 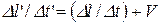 (7)
(7)
несовместимо с условиями  .
.
Нужно либо считать, что  , т. е. поезд с точки зрения стрелочника стал короче, либо время
, т. е. поезд с точки зрения стрелочника стал короче, либо время  в движущейся системе идет медленнее, т. е.
в движущейся системе идет медленнее, т. е. 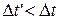 . Оказывается, имеет место и то и другое одновременно.
. Оказывается, имеет место и то и другое одновременно.
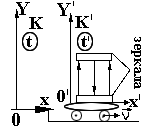 Покажем, что движущиеся часы идут медленнее. Для этого рассмотрим две инерциальные системы отсчета K и K'. Систему K будем считать покоящейся, а систему K' – движущейся со скоростью V, (см. рис. 2).
Покажем, что движущиеся часы идут медленнее. Для этого рассмотрим две инерциальные системы отсчета K и K'. Систему K будем считать покоящейся, а систему K' – движущейся со скоростью V, (см. рис. 2).
Предположим, что в системе
K находятся часы в виде двух параллельных зеркал и источника света. Они неподвижны в системе
K'. Свет включается на короткое время и начинает двигаться вверх и вниз, попеременно отражаясь от верхнего и нижнего зеркал, (см. рис. 2.). В таких часах качающимся маятником является луч света.
Рассмотрим один из полупериодов, когда свет движется сверху вниз. Пусть с точки зрения наблюдателя системы K' это происходит за время Dt', тогда расстояние между зеркалами будет  , причем оно будет поперечным, как по отношению системы K', так и системы K, и поэтому одинаковым в этих системах. Однако с точки зрения наблюдателя системы K свет распространяется наклонно, т. е. свет будет снесен вправо на расстояние VDt.
, причем оно будет поперечным, как по отношению системы K', так и системы K, и поэтому одинаковым в этих системах. Однако с точки зрения наблюдателя системы K свет распространяется наклонно, т. е. свет будет снесен вправо на расстояние VDt. 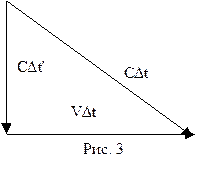
Из рис. 3 по теореме Пифагора находим  , откуда
, откуда
 , (8)
, (8)
где 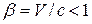 , т. е. движущиеся часы идут медленнее, чем неподвижные.
, т. е. движущиеся часы идут медленнее, чем неподвижные.
Подтверждением этого служит время жизни движущихся мюонов; собственное время их жизни  мкс, а по часам неподвижным относительно Земли - значительно больше:
мкс, а по часам неподвижным относительно Земли - значительно больше:
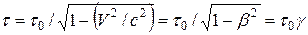 , (9)
, (9)
где V – скорость мюона относительно Земли,  – коэффициент Лоренца,
– коэффициент Лоренца, 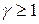 .
.
Подобным образом можно показать, что размеры тел в направлении движения сокращаются, т. е.
 . (10)
. (10)
Исходя из двух постулатов, Эйнштейн в 1905 г. вывел преобразования Лоренца (полученные Лоренцом в 1904 г. как преобразования, по отношению к которым уравнения классической микроскопической электродинамики – уравнения Лоренца- Максвелла сохраняют свой вид).
Напишем их подобно преобразованиям Галилея:
 , (11)
, (11)
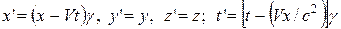 . (12)
. (12)
Для медленных движений, когда 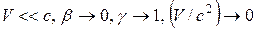 преобразования Лоренца переходят в преобразования Галилея. Используя соотношения (11), (12), можно показать, что пространственные расстояния при преобразованиях Лоренца изменяются, т. е.
преобразования Лоренца переходят в преобразования Галилея. Используя соотношения (11), (12), можно показать, что пространственные расстояния при преобразованиях Лоренца изменяются, т. е.  , где
, где
 (13)
(13)
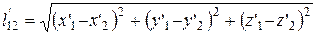 . (14)
. (14)
Этот эффект называется лоренцевым сокращением длины.
Неизменным (инвариантным) при преобразованиях Лоренца остается так называемый интервал между событиями
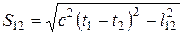 .(15)
.(15)
Все темы данного раздела:
Л Е К Ц И Я № 1. К И Н Е М А Т И К А
Кинематика – это раздел механики, в котором изучается движение тел без рассмотрения причин, вызывающих движение.
Движением тела называют изменение его положения относительно другого тела в
Кинематика материальной точки. Путь, перемещение, скорость и ускорение
Рис. 1
Изуч
Закон движения дается векторным уравнением
. (1)
При координатном способе положение точки А определяется координатами x, y, z, а зако
Скорость
Мгновенная скорость материальной точки определяется соотношением
Ускорение
Для характеристики быстроты изменения скорости вводится векторная физическая величина, называемая ускорением
Угловая скорость и угловое ускорение
Рассмотрим движение материальной точки по окружности радиуса R (рис. 5). Пусть за время
Л Е К Ц И Я № 2 . Д И Н А М И К А М А Т Е Р И А Л Ь Н О Й Т О Ч К И
Динамика – это раздел механики, посвященный изучению движения материальных тел под действием приложенных к ним сил.
В основе динамики лежат 3 закона Ньютона, сформулированные в 1687 г. Они
Второй закон Ньютона
Для того, чтобы его сформулировать введем понятие силы.
Силой называется векторная величина, характеризующая воздействие на данное тело со стороны других тел.
Сила
Третий закон Ньютона
Воздействие тел друг на друга всегда носит характер взаимодействия. Если тело 2 действует на тело 1 с силой
Силы трения
Они появляются при перемещении соприкасающихся тел или их частей друг относительно друга.
Трение, воз
Л Е К Ц И Я № 3. З А К О Н С О Х Р А Н Е Н И Я И М П У Л Ь С А
Совокупность тел, выделенных для рассмотрения, называется механической системой.
Тела системы могут взаимодействовать как между собой, так и с телами, не входящими в систему. В соо
Закон сохранения импульса
Рассмотрим систему, состоящую из n материальных точек. Обозначим через силу, с которой материальная точка
Центр масс и закон его движения
В динамике широко используется понятие центра масс системы материальных то чек, который обычно обозначают буквой С. Положение центра масс определяется радиусом-вектором
Реактивное движение. Движение тел с переменной массой
Имеется много явлений, в основе которых лежит закон сохранения импульса. Например, полет ракет (и работа реактивных двигателей) основаны на том, что в результате выбрасывания из сопла газов, ракете
Консервативные и неконсервативные силы
Все силы, встречающиеся в механике , принято разделять на консервативные и неконсервативные.
Сила, дейс
Потенциальная энергия системы материальных точек
Рассмотрим систему, состоящую из многих материальных точек. Если задано положение каждой материальной точки, то этим определено и положение всей системы или ее конфигурация. Если силы, действующие
Потенциальная энергия растянутой пружины
Обозначим через х растяжение пружины, т.е. разность длин пружины в деформированном и недеформированном состояниях.
При возвращении пружины из деформированного состояния в недеформир
Потенциальная энергия тела в однородном поле силы тяжести Земли
Формула (15) справедлива также для однородных сферических тел; в этом случае r – расстояние между центрами масс таких тел. В частности, потенциальная энергия тела массы т, находящегос
Кинетическая энергия
Напишем уравнение движения материальной точки (частицы) массы m, движущейся под действием сил, результирующая которых равна
Закон сохранения энергии в механике
Рассмотрим систему из n материальных точек, на которые действуют как консервативные так и неконсервативные силы. Найдем работу, которую совершают эти силы при перемещении системы из одной ко
Упругое и неупругое соударения
При соударении тел они в большей либо меньшей мере деформируются. При этом кинетическая энергия тел частично или полностью переходит в потенциальную энергию упругой деформации и во внутреннюю энерг
Абсолютно неупругий удар
Интересным примером, где имеет место потеря механической энергии под действием диссипативных сил, является абсолютно неупругий удар, при котором потенциальная энергия упругой деформации не возникае
Абсолютно упругий удар
Это такой удар, при котором полная механическая энергия тел сохраняется. Сначала кинетическая энергия частично или полностью переходит в потенциальную энергию упругой деформации. Затем тела возвращ
Общефизический закон сохранения энергии
Классическая механика учитывает только кинетическую энергию макроскопического движения тел и их макроскопических частей, а также их потенциальную энергию. Но она полностью отвлекается от внутреннег
Момент силы и момент импульса относительно неподвижного начала
Пусть О – какая-либо неподвижная точка в инерциальной системе отсчета. Ее называют началом или полюсом. Обозначим через
Уравнение моментов
Предположим, что точка О неподвижна. В случае одной материальной точки, дифференцируя (3), получаем
.
Закон сохранения момента импульса
Если система замкнута (т. е. внешних сил нет), то и, следовательно, согласно уравнению (6) вектор
Движение в поле центральных сил
Если на материальную точку действует сила вида
, (8)
то говорят, что материальная точка находит
Степени свободы. Обобщенные координаты
Положение точки в пространстве можно задать некоторым числом независимых координат, например, тремя координатами х, у, z декартовой системы. Но это можно сделать и иначе. Например, вместо пр
Число степеней свободы твердого тела
Абсолютно твердым телом в механике называют идеализированную систему материальных точек, все расстояния между которыми при движении системы не изменяются с течением времени.
Чтобы однознач
Уравнение движения и равновесия твердого тела
Так как твердое тело является механической системой с шестью степенями свободы, то для описания его движения требуется шесть независимых числовых уравнений или два независимых векторных уравнения.
Теорема Штейнера
В механике твердое тело обычно рассматривают как механическую систему, масса т которой непрерывно распределена по объему V тела, так что при вычислении момента инерции тела, суммирова
Кинетическая энергия при плоском движении
Плоским (плоскопараллельным) называется такое движение, при котором все точки тела движутся в параллельных плоскостях. Представим плоское движение тела как поступательное движение со скоростью
Просуммировав по всем материальным точкам, получим
или , (12)
Таким образом, если разбить плоское движение тела на поступательное со
скоростью центра масс Vc и вращательное с угловой скоростью w вокруг оси, проходящей через центр масс тела, то кинетическая энергия распадается на два независимых слагаемых
Мощность
. (16)
Сопоставим основные величины и уравнения поступательного и вращательного движений
Преобразования Галилея. Принцип относительности Галилея
Если системы отсчета движутся относительно друг друга равномерно и прямолинейно и в одной из них справедлив 1- й закон Ньютона, то эти системы являются инерциальными. Галилей установил:
Постулаты частной теории относительности
Исторически именно закон сложения скоростей (5) показал ограниченность галилеевых представлений о свойствах пространства и времени.
Действительно, согласно этому закону по отношению к сист
Закон сложения скоростей в релятивистской механике
Дифференцируя (11) по , а (12) по
Масса в ньютоновской и релятивистской механике
При изучении движения тел, скорости vкоторых пренебрежимо малы по сравнению со скоростью света с (v/c → 0), имеет место нерелятивистское приближение. В этом случ
Энергия, импульс в релятивистской механике
Если тело движется со скоростью v относительно инерциальной системы отсчета (ИСО) K, то помимо энергии покоя
Основное уравнение релятивистской динамики
Согласно (20), релятивистский импульс , при этом обе формулы справедливы для «тяжелых», т.е. имеющих не н
Кинетическая энергия релятивистской частицы
Согласно (19), полная энергия тела (частицы) в релятивистской механике , она складывается из энер
Гармонические колебания
Рис. 1
Изуч
Потенциальная и кинетическая энергии
Установим изменение потенциальной и кинетической энергий колеблющейся системы. Известно, что потенциальная энергия упруго деформированного тела равна
Векторная диаграмма гармонического колебания
Гармоническое колебание
можно представить в виде проекции вектора
Комплексная форма представления колебаний
Согласно формуле Эйлера для комплексных чисел
Сложение одинаково направленных колебаний
Рассмотрим сложение двух гармонических колебаний одинаковой частоты, смещения которых и
Математический маятник
Это материальная точка, подвешенная на невесомой, нерастяжимой нити.
Хорошим приближением к мате
Пружинный маятник
Это груз массой т , подвешенный на абсолютно упругой пружине и совершающий колебания около положения равновесия, рис. 1. Он был рассмотрен в параграфе 1. Для него
Свободные затухающие колебания
Кроме силы упругости F = - kx на тело действуют также сила сопротивления, которая при медленных движениях пропорциональна скорости, т. е.
Логарифмический декремент затухания
Натуральный логарифм отношения отклонения системы в моменты времени t и называется логарифмическим декрем
Вынужденные колебания
Они возникают при действии на систему внешней периодически изменяющейся силы (вынуждающей силы) , (22)
 машинист этот сигнал регистрирует, тогда скорость света
машинист этот сигнал регистрирует, тогда скорость света  , где
, где  – длина поезда в системе K'.
– длина поезда в системе K'. время, отсчитываемое стрелочником. Что касается пути, пройденного светом с точки зрения стрелочника, то он состоит из длины поезда
время, отсчитываемое стрелочником. Что касается пути, пройденного светом с точки зрения стрелочника, то он состоит из длины поезда  , движущегося со скоростью V, и расстояния Vdt, на которое за время
, движущегося со скоростью V, и расстояния Vdt, на которое за время  хвостовой вагон отъедет от стрелочника.
хвостовой вагон отъедет от стрелочника. .
.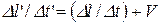 (7)
(7) .
. , т. е. поезд с точки зрения стрелочника стал короче, либо время
, т. е. поезд с точки зрения стрелочника стал короче, либо время  в движущейся системе идет медленнее, т. е.
в движущейся системе идет медленнее, т. е. 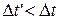 . Оказывается, имеет место и то и другое одновременно.
. Оказывается, имеет место и то и другое одновременно. Покажем, что движущиеся часы идут медленнее. Для этого рассмотрим две инерциальные системы отсчета K и K'. Систему K будем считать покоящейся, а систему K' – движущейся со скоростью V, (см. рис. 2).
Покажем, что движущиеся часы идут медленнее. Для этого рассмотрим две инерциальные системы отсчета K и K'. Систему K будем считать покоящейся, а систему K' – движущейся со скоростью V, (см. рис. 2). , причем оно будет поперечным, как по отношению системы K', так и системы K, и поэтому одинаковым в этих системах. Однако с точки зрения наблюдателя системы K свет распространяется наклонно, т. е. свет будет снесен вправо на расстояние VDt.
, причем оно будет поперечным, как по отношению системы K', так и системы K, и поэтому одинаковым в этих системах. Однако с точки зрения наблюдателя системы K свет распространяется наклонно, т. е. свет будет снесен вправо на расстояние VDt. 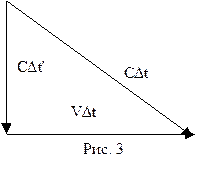
 , откуда
, откуда , (8)
, (8)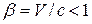 , т. е. движущиеся часы идут медленнее, чем неподвижные.
, т. е. движущиеся часы идут медленнее, чем неподвижные. мкс, а по часам неподвижным относительно Земли - значительно больше:
мкс, а по часам неподвижным относительно Земли - значительно больше: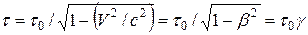 , (9)
, (9) – коэффициент Лоренца,
– коэффициент Лоренца, 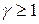 .
. . (10)
. (10) , (11)
, (11)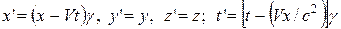 . (12)
. (12)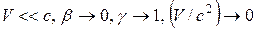 преобразования Лоренца переходят в преобразования Галилея. Используя соотношения (11), (12), можно показать, что пространственные расстояния при преобразованиях Лоренца изменяются, т. е.
преобразования Лоренца переходят в преобразования Галилея. Используя соотношения (11), (12), можно показать, что пространственные расстояния при преобразованиях Лоренца изменяются, т. е.  , где
, где (13)
(13)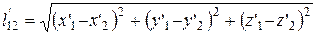 . (14)
. (14)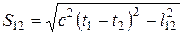 .(15)
.(15)






Новости и инфо для студентов