Указания к выполнению контрольной задачи К1
Задача К1- на определение кинематических характеристик точки по заданным в координатной форме уравнениям движения. Варианты задач различаются траекториями, которыми являются окружности, параболы, эллипсы, прямые. Все эти случаи рассмотрены в предложенных примерах 2.1-2.5. Задачи на определение кинематических характеристик точки при координатном способе задания ее движения необходимо решать в следующей последовательности:
1) выбрать систему координат;
2) исключив время из уравнений движения точки, определить уравнение траектории точки и изобразить ее график;
3) определить на графике положение точки в заданный момент времени;
4) по заданным уравнениям движения точки определить проекции скорости точки и модуль скорости по формулам (2.3) и (2.4) соответственно;
5) построить на рисунке вектор скорости точки в заданный момент времени;
6) по формулам (2.5) и (2.6) определить ускорение точки;
7) построить на рисунке вектор ускорения точки в заданный момент времени;
8) взять производную по времени от модуля скорости и составить выражение для квадрата касательного ускорения;
9) используя формулу (2.10), вычислить нормальное ускорение;
10) используя формулу нормального ускорения (2.9), вычислить радиус кривизны траектории в заданный момент времени;
11) разложить ускорение точки на касательную и нормальную составляющие на рисунке;
12) определить по касательному ускорению характер движения точки в заданный момент времени.
Пример 2.1.Движение точки М в плоскости xy задано уравнениями
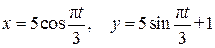 (2.11)
(2.11)
(x, y – в см, t – в с).
Определить траекторию точки и для момента времени t1 = 1 с найти положение точки M на траектории, ее скорость, полное, касательное и нормальное ускорения. Определить также радиус кривизны траектории в точке М.
Решение. Определим траекторию точки М, исключив из уравнений движения (2.11) время t. C этой целью приведем уравнения (2.11) к виду:
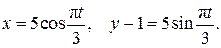
Возведем оба уравнения во вторую степень и сложим:
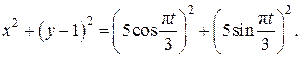
Так как 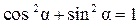 , имеем уравнение вида
, имеем уравнение вида
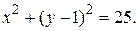 (2.12)
(2.12)
Траекторией точки является окружность радиуса 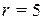 с центром О1(0,1) (рис. 2.4).
с центром О1(0,1) (рис. 2.4).
Определим начальное положение точки М0: при t = 0
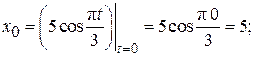
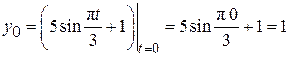 .
.
В момент времени t1 = 1 с точка М имеет координаты:
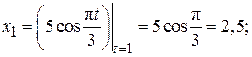
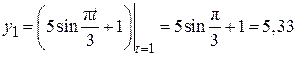 .
.
Определим проекции скорости точки по формулам (2.3):
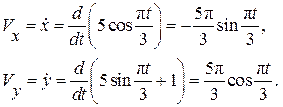 (2.13)
(2.13)
По формуле (2.4) вычислим модуль скорости:
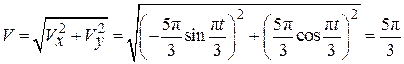 . (2.14)
. (2.14)
Определим проекции и модуль скорости в момент времени t1 = 1 с:
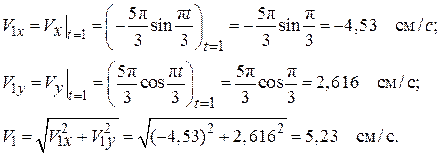
Вектор скорости строим (рис. 2.4) по составляющим:
 .
.
 |
Рис. 2.4
Определим проекции ускорения точки М, вычисляя производные по времени от проекции ее скорости (2.13):
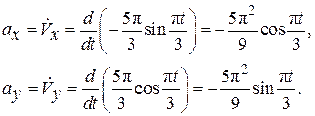
При t =1 c имеем
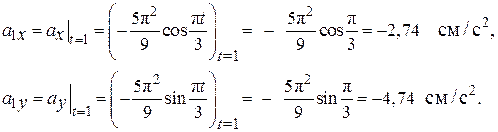
По формуле (2.6) определим модуль ускорения:
Вектор ускорения 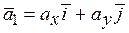 направлен вниз. Найдем производную от функции скорости (2.14) по времени:
направлен вниз. Найдем производную от функции скорости (2.14) по времени:
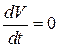 .
.
При t1 = 1 с 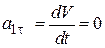 .
.
Вычислим нормальное ускорение по формуле (2.10):
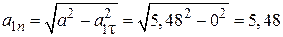 см/с2.
см/с2.
Радиус кривизны вычислим по формуле (2.9)
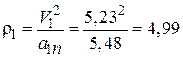 см.
см.
Следовательно, точка движется равномерно и 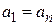 . Вектор ускорения направлен к центру окружности. Совпадение расчетного радиуса кривизны окружности с радиусом окружности служит контролем правильности решения.
. Вектор ускорения направлен к центру окружности. Совпадение расчетного радиуса кривизны окружности с радиусом окружности служит контролем правильности решения.
Пример 2.2.Движение точки М в плоскости xy задано уравнениями
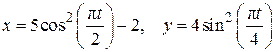 (2.15)
(2.15)
(x, y – в см, t – в с).
Определить траекторию точки и для момента времени t1 = 1/2 с найти положение точки M на траектории, ее скорость, полное, касательное и нормальное ускорения. Определить также радиус кривизны траектории в точке М.
Решение. Определим траекторию точки М, исключив из уравнений движения (2.15) время t. C этой целью преобразуем уравнения (2.15), приведя тригонометрические функции к одному аргументу, используя при этом тригонометрическую формулу 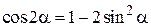 . В результате получим уравнение вида
. В результате получим уравнение вида
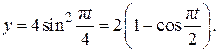 (2.16)
(2.16)
Или
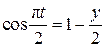 .
.
Подставляя (2.16) в первое уравнение (2.15), получим 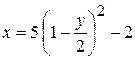 или
или 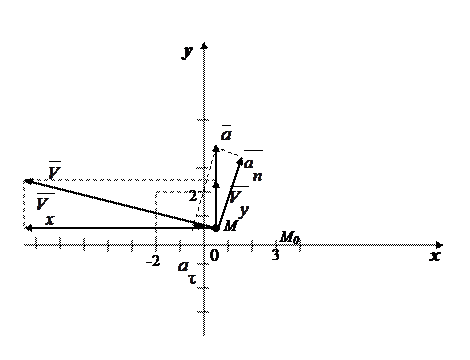
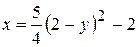 .
.
Траекторией точки является парабола (рис. 2.5)
 |
Рис. 2.5
Определим начальное положение точки М0: при t = 0
x0 = 5cos20 – 2 = 3; y0 = 4sin20 = 0.
| |
x1 = 5 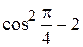 = 0,5; y1 = 4
= 0,5; y1 = 4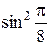 = 0,59.
= 0,59.
Определим проекции скорости точки по формулам (2.3):
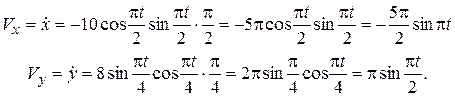 , (2.17)
, (2.17)
По формуле (2.4) вычислим модуль скорости:
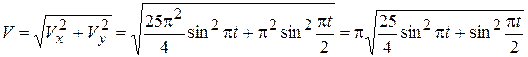 . (2.18)
. (2.18)
Определим проекции и модуль скорости в момент времени t1 = 1/2 с:
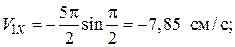 ;
; 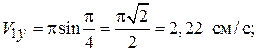 ;
;
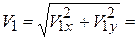
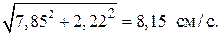
Вектор скорости строим (рис. 2.5) по составляющим:
 .
.
Определим проекции ускорения точки М, вычисляя производные по времени от проекции ее скорости (2.17):
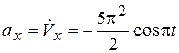 ,
, 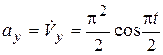 .
.
По формуле (2.6) определим модуль ускорения:
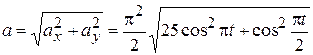 .
.
При t1 =1/2 с
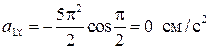 ,
,  ,
,
следовательно, a1 = 3,48 см/с2 и вектор ускорения 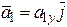 направлен вертикально вверх.
направлен вертикально вверх.
Найдем производную от функции скорости (2.18) по времени:
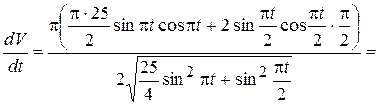
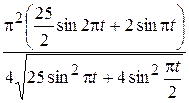 .
.
При t1 = 1/2 с 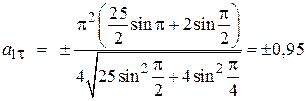 .
.
Учитывая, что 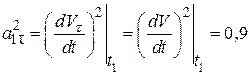 , вычислим нормальное ускорение по формуле (2.10):
, вычислим нормальное ускорение по формуле (2.10):

Радиус кривизны вычислим по формуле (2.9)
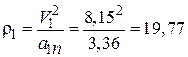 см.
см.
Разложим вектор ускорения 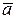 на нормальную и касательную составляющие на рис. 2.5:
на нормальную и касательную составляющие на рис. 2.5: 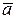 =
= 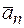 +
+ 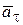 .
.
Поскольку векторы скорости и касательного ускорения направлены в одну сторону, точка в данный момент времени движется ускоренно.
Пример 2.3.Движение точки М в плоскости xy задано уравнениями
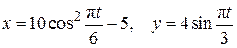 (2.19)
(2.19)
(x, y – в см, t– в с).
Определить траекторию точки, и для момента времени t1 = 1 с найти положение точки M на траектории, ее скорость, полное, касательное и нормальное ускорения. Определить также радиус кривизны траектории в точке М.
Решение. Определим траекторию точки М, исключив из уравнений движения (2.19) время t. C этой целью преобразуем уравнения (2.19), используя при этом тригонометрическую формулу 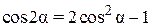 :
:
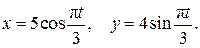
Уравнение траектории будет иметь вид
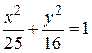 . (2.20)
. (2.20)
Для получения уравнения (2.20) использовали тригонометрическую формулу 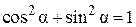 .
.
Траекторией точки является эллипс (рис. 2.6).
Определим начальное положение точки М0: при t = 0
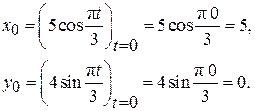
В момент времени t1 = 1 с точка М имеет координаты:
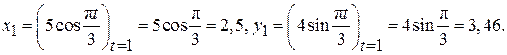

Рис. 2.6
Определим проекции скорости точки по формулам (2.3):
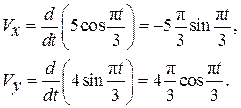 (2.21)
(2.21)
По формуле (2.4) вычислим модуль скорости:
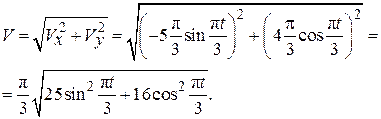 (2.22)
(2.22)
Определим проекции и модуль скорости в момент времени t1 = 1 с:
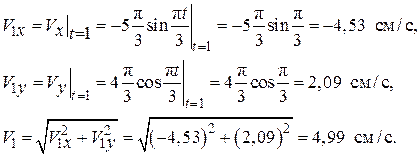
Вектор скорости строим (рис. 2.6) по составляющим:
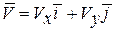 .
.
Определим проекции ускорения точки М, вычисляя производные по времени от проекции ее скорости (2.13):
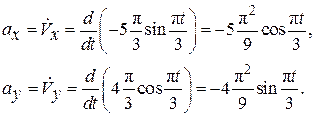
По формуле (2.6) определим модуль ускорения:
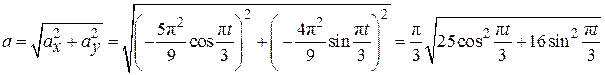 .
.
При t1 = 1 с имеем
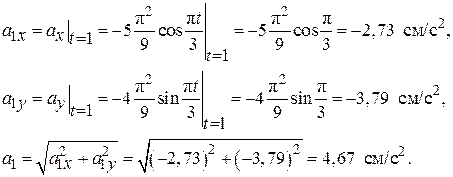
Найдем производную от функции скорости (2.14) по времени:
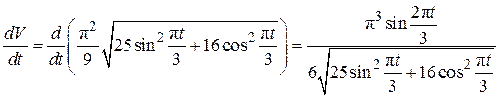 .
.
При t1 = 1 с 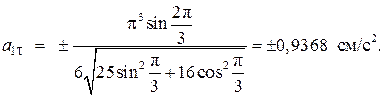
Учитывая, что 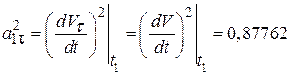 , вычислим нормальное ускорение по формуле (2.10):
, вычислим нормальное ускорение по формуле (2.10):
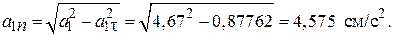
Радиус кривизны вычислим по формуле (2.9)
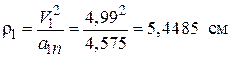 .
.
Разложим вектор ускорения 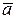 на нормальную и касательную составляющие на рис. 2.6:
на нормальную и касательную составляющие на рис. 2.6: 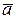 =
= 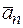 +
+ 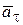 .
.
Поскольку векторы скорости и касательного ускорения направлены в одну сторону, точка в данный момент времени движется ускоренно.
Пример 2.4.Движение точки М в плоскости xy задано уравнениями
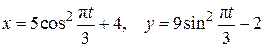 (2.23)
(2.23)
(x, y – в см, t – в с).
Определить траекторию точки и для момента времени t1 = 1 с, найти положение точки M на траектории, ее скорость, полное, касательное и нормальное ускорения. Определить также радиус кривизны траектории в точке М.
Решение. Определим траекторию точки М, исключив из уравнений движения (2.23) время t. C этой целью преобразуем уравнения (2.23) к виду
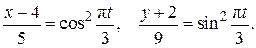 (2.24)
(2.24)
Сложим уравнения (2.24), применив тригонометрическое тождество 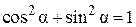 , получим
, получим
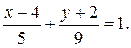
Или 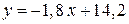 .
.
Траекторией точки является прямая (рис. 2.7)
Определим начальное положение точки М0: при t = 0
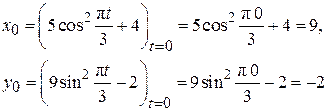
В момент времени t1 = 1 с точка М имеет координаты:

Определим проекции скорости точки по формулам (2.3):
|
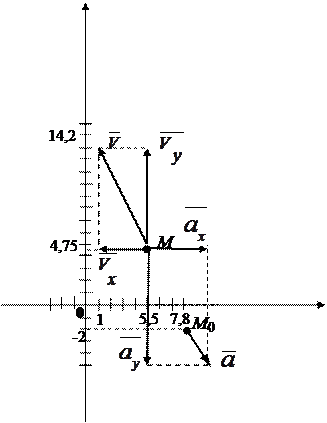
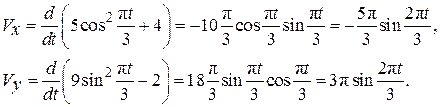 (2.25)
(2.25)
 |
Рис. 2.7
По формуле (2.4) вычислим модуль скорости:
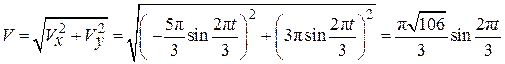 . (2.26)
. (2.26)
Определим проекции и модуль скорости в момент времени t1 = 1 с:
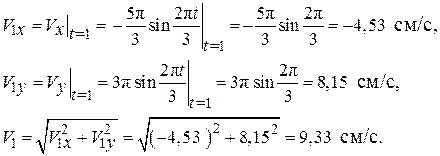
Вектор скорости строим (рис. 2.7) по составляющим:
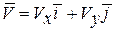 .
.
Определим проекции ускорения точки М, вычисляя производные по времени от проекции ее скорости (2.25):

По формуле (2.6) определим модуль ускорения:
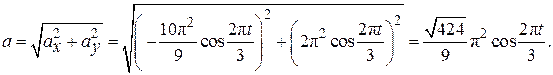
При t1=1 с имеем
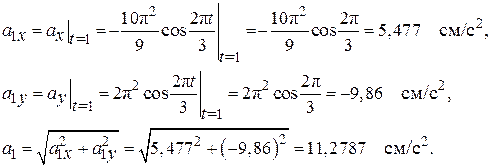
При прямолинейном движении точки радиус кривизны траектории r = µ и следовательно,
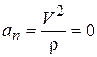 .
.
Поскольку векторы скорости и ускорения направлены в разные стороны, точка в данный момент времени движется замедленно.
Пример 2.5.Движение точки М в плоскости xy задано уравнениями
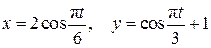 (2.27)
(2.27)
(x, y – в см, t – в с).
Определить траекторию точки и для момента времени t1 = 2 с найти положение точки M на траектории, ее скорость, полное, касательное и нормальное ускорения. Определить также радиус кривизны траектории в точке М.
Решение. Определим траекторию точки М, исключив из уравнений движения (2.27) время t. C этой целью преобразуем уравнения (2.27), применив тригонометрическое тождество 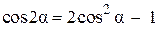 к виду
к виду
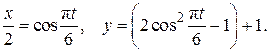 (2.28)
(2.28)
Или
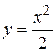 .
.
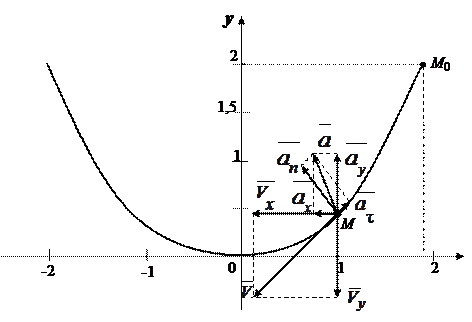 траекторией точки является парабола (рис. 2.8).
траекторией точки является парабола (рис. 2.8).
Рис. 2.8
Определим начальное положение точки М0: при t = 0

В момент времени t1 = 2 с точка М имеет координаты:
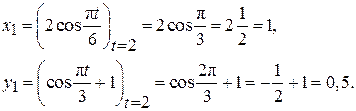
Определим проекции скорости точки по формулам (2.3):
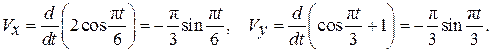 (2.29)
(2.29)
По формуле (2.4) вычислим модуль скорости:
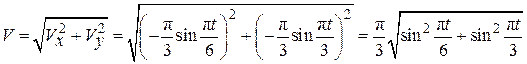 . (2.30)
. (2.30)
Определим проекции и модуль скорости в момент времени t1 = 2 с:
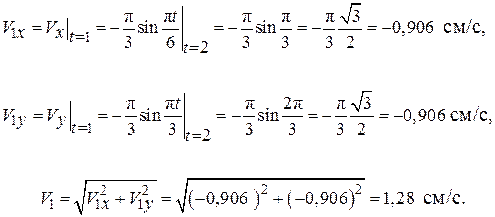
Вектор скорости строим (рис. 2.8) по составляющим:
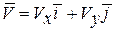 .
.
Определим проекции ускорения точки М, вычисляя производные по времени от проекции ее скорости (2.29):

По формуле (2.6) определим модуль ускорения:
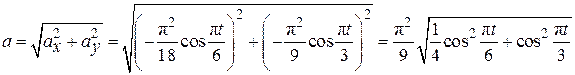 .
.
При t1 = 2 с имеем
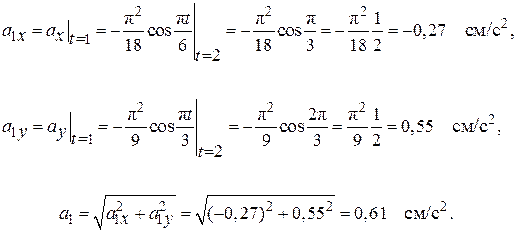
Найдем производную от функции скорости (2.30) по времени:
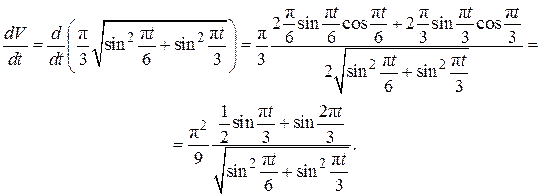 .
.
При t1 = 2 с
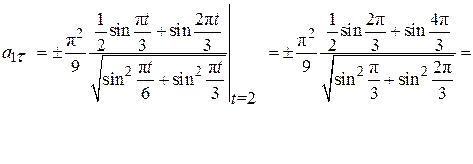
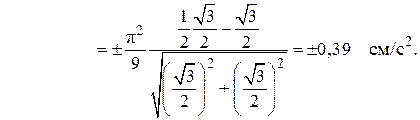
Учитывая, что 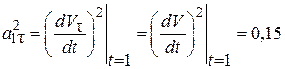 , вычислим нормальное ускорение по формуле (2.10):
, вычислим нормальное ускорение по формуле (2.10):
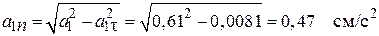 .
.
Радиус кривизны вычислим по формуле (2.9)
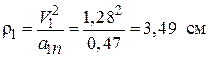 .
.
Разложим вектор ускорения 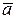 на нормальную и касательную составляющие на рис. 2.8:
на нормальную и касательную составляющие на рис. 2.8: 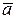 =
= 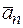 +
+ 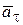 .
.
Поскольку векторы скорости и касательного ускорения направлены в разные стороны, точка в данный момент времени движется замедленно.