Квантово-механический осциллятор

 

Атомы в молекулах и кристаллах осуществляют колебания возле положения равновесия. При малых смещениях на атом действует сила, которая пропорциональная смещению , где – коэффициент возвращающей силы.

Следовательно, потенциальная энергия изменяется по квадратичному закону

. (1.125)

 

И нахождение возможных значений энергии колеблющейся частицы (осциллятора) сводится к решению уравнения Шредингера для частицы в потенциальной яме параболической формы (рис.1.6)

 

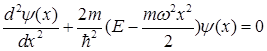. (1.126)

 

 

а	б	в
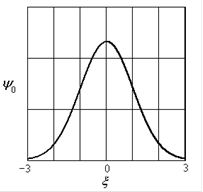
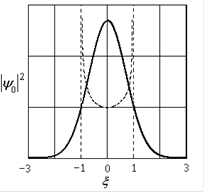
Рис.1.6. Энергия квантового осциллятора (а) и волновая функция (б) и распределение плотности вероятности (в) для основного состояния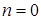

 

Решение (1.126) удобно проводить, воспользовавшись новыми обозначениями и безразмерной переменной

 

 

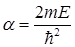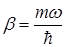, , . (1.127)

 

 

В этих обозначениях уравнение (1.126) приобретает вид

 

. (1.128)

 

Важным отличием осциллятора от рассмотренных выше примеров является то, что в этом случае движение частицы не ограничено какой-либо непроницаемой стенкой. Поэтому для осциллятора нет граничных условий, подобных (1.109). Единственным условием, которое налагается на волновую функцию осциллятора, есть требование ее квадратичной интегрируемости.

Решение (1.128) сначала будем искать для больших , когда 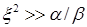. Тогда в (1.128) можно отбросить , и уравнение с достаточной точностью удовлетворяется решением

 

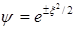. (1.129)

 

Действительно, имеем

 

.

 

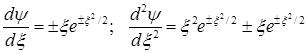При второй член в правой части последнего равенства несущественен сравнению с первым, следовательно, уравнение (1.128) асимптотически удовлетворяется решениям (1.129). Из физических соображений решения со знаком плюс отбрасываем.

Попробуем искать решение (1.128) в виде

 

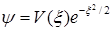, (1.130)

 

где – неизвестная функция.

 

 

Подстановка (1.130) приводит (1.128) к уравнению

 

. (1.131)

 

Решение ищем в виде степенного ряда

 

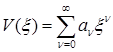. (1.132)

 

Подставим (1.132) в (1.131) и получим

 

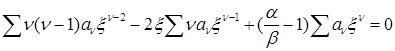. (1.133)

 

Степенный ряд будет равняться нулю в том случае, когда все его коэффициенты обращаются в нуль. Полагая равным нулю коэффициент при , получим рекуррентную формулу

 

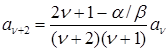. (1.134)

 

При , 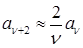и ряд (1.133) ведет себя, как 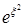. Функция (1.130) при этом неограниченно растет.

Чтобы получить решение, которое отвечает необходимым условиям конечности, необходимо ряд свести к полиному. Допустим, что 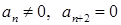, начиная с некоторого . Тогда последующие коэффициенты обращаются в нуль и функция 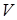сводится к полиному -й степени.

Из (1.134) следует, что при этом выполняется условие

 

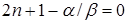, (1.135)

 

где – целое число ().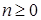

Воспользовавшись (1.127), получим

 

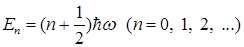. (1.136)

 

Функция представляет полиномы –й степени, которые носят название полиномов Эрмита и обозначаются как 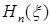. Они удовлетворяют дифференциальное уравнение

, (1.137)

 

которое получается из (1.131) с учетом (1.135). Полиномы Эрмита определяются формулой

 

. (1.138)

 

Например, , , .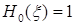

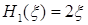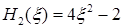Для вычисления полиномов удобно пользоваться рекуррентной формулой, которая позволяет по двум полиномами вычислить третий

 

. (1.139)

 

Нормировка для полиномов Эрмита имеет вид

 

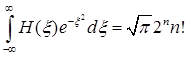. (1.140)

 

Волновая функция для –го энергетического состояния приобретает вид

 

, (1.141)

где 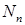– нормирующий множитель, который может быть вычислен из условий нормировки волновой функции (1.6) и полиномов Эрмита (1.140). Таким образом, решение (1.126) запишется как

 

. (1.142)

 

Для основного состояния (n=0) волновая функция имеет вид

 

,

 

а плотность вероятности (рис.1.6, в)

 

.

 

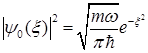Из распределения – типа гауссовой кривой ошибок – можно сделать вывод, что в основном состоянии (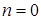) частица большее время находится около положения равновесия (). Но, что интересно, существует конечная вероятность найти частицу не только в границах отрезка, который равняется удвоенной амплитуде колебаний классического осциллятора, но и в «запрещенных» областях (справа и слева от вертикальных пунктирных прямых), в которых потенциальная энергия частицы больше полной (рис.1.6, в).

Сравним с этой кривой соответствующую кривую распределения вероятности найти макроскопическую частицу, которая совершает гармонические колебания, в каком-либо месте пути. Вероятность найти частицу в определенном месте обратно пропорциональная ее скорости, то есть 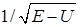, где 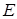– полная энергия, 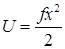– потенциальная энергия. Соответствующая кривая изображена пунктиром на рис.1.6, в; она существенно отличается от кривой для квантового осциллятора.

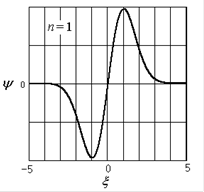
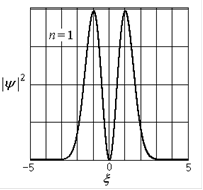
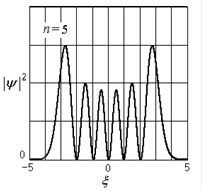
Вид волновых функций и распределение плотности вероятности для возбужденных состояний () представлены на рис.1.7. При малых значениях квантовых чисел квантовый осциллятор ведет себя иначе, чем классический. Напротив, чем больше , тем в большей мере квантовое распределение вероятности приближается к классическому (см. рис.1.7 для ).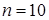

Если провести непрерывную кривую через максимумы квантового распределения, то она будет приблизительно параллельна классической кривой. При последующем увеличенные максимумы сближаются, и ход кривой все больше приближается к классическому.

Сделаем выводы из полученного решения:

- спектр энергии квантового осциллятора дискретен (ф-ла 1.136);

- спектр равномерен с расстоянием между соседними уровнями (таким образом известный постулат Планка об излучении и поглощении энергии квантами автоматически следует из решения уравнения Шредингера);

- «нулевая» энергия квантового осциллятора отлична от нуля и равна 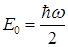(это является следствием принципа неопределенностей).

 

Рис.1.7. Волновые функции и распределение плотности вероятности для некоторых возбужденных состояний квантового осциллятора