Микрочастица в потенциальной яме конечной глубины
Потенциальное поле ямы имеет вид  при
при 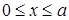 ,
, 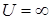 при
при 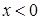 и
и  при
при  (рис.1.8, а). Частица, которая находится в такой яме с энергией
(рис.1.8, а). Частица, которая находится в такой яме с энергией  , будет все время с ней связана.
, будет все время с ней связана.
Решение стационарного уравнения Шредингера имеет вид
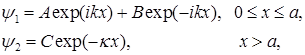 (1.143)
(1.143)
где 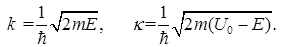 (1.144)
(1.144)
|
|
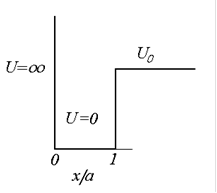
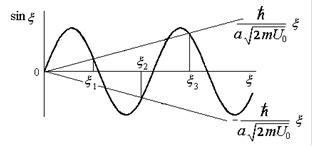
| а | б |
| Рис.2.8. Потенциальная яма конечной глубины (а) и графоаналитическое решение дисперсионного уравнения (б) |
Воспользовавшись условиями
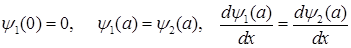 , (1.145)
, (1.145)
получим уравнение
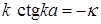 . (1.146)
. (1.146)
Преобразуем (1.146) в уравнение более удобное для анализа:
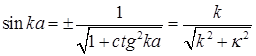 .
.
Обозначим  и с учетом
и с учетом 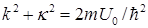 , получим
, получим
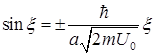 . (1.147)
. (1.147)
В качестве решения берем не все точки пересечения синусоиды с прямыми, а только те, знак которых согласуется со знаком первичного уравнения (1.146). Этим значением 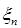 отвечает конечное число собственных значений энергии
отвечает конечное число собственных значений энергии
 . (1.148)
. (1.148)
Если яма мелкая или достаточно узкая, то может случиться, что решение уравнения (1.146) отсутствует, то есть частица не может удержаться внутри ямы.
В классической механике частица с энергией  не может выйти за пределы ямы. В квантовой механике существует вероятность найти частицу за пределами ямы, если даже
не может выйти за пределы ямы. В квантовой механике существует вероятность найти частицу за пределами ямы, если даже  . Как пример, на рис.1.9 показаны волновая функция и распределение плотности вероятности для основного и возбужденного состояний электрона в потенциальной яме конечной глубины.
. Как пример, на рис.1.9 показаны волновая функция и распределение плотности вероятности для основного и возбужденного состояний электрона в потенциальной яме конечной глубины.

| 
|
| а | б |
| Рис.1.9. Волновая функция и распределение плотности вероятности для основного (а) (~7еВ) и возбужденного (б) (~27еВ) состояний электрона в потенциальной яме (а=0,2 нм, U0=40 эВ). |