Свободное движение микрочастицы
Рассмотрим некоторые самые простые случаи движения микрочастицы в потенциальных полях. Начнем со свободного движения.
Оператор Гамильтона в этом случае имеет вид
 .
.
Представляя волновую функцию в виде
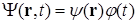 (1.61))
(1.61))
и используя метод разделения переменных, получим функцию  , которая зависит от времени
, которая зависит от времени
 , (1.62)
, (1.62)
и амплитудное уравнение Шредингера (или уравнение для стационарных состояний)
 . (1.63)
. (1.63)
Систему координат выбираем таким образом, чтобы направление движения частицы совпадало с осью  . Тогда решение уравнения (1.63) будет иметь вид
. Тогда решение уравнения (1.63) будет иметь вид
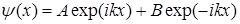 , (1.64)
, (1.64)
где 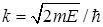 (по физическому содержанием это волновой вектор).
(по физическому содержанием это волновой вектор).
Значения энергии, как видно из (1.64) оказываются двукратно вырожденными. Это вырождение снимается, если потребовать, чтобы кроме энергии в этом состоянии имела определенные значения еще какая-либо физическая величина, например, импульс. Тогда частице, которая движется в положительном направлении оси  , соответствуют импульс
, соответствуют импульс 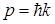 и энергия
и энергия 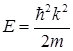 . Им отвечает собственная волновая функция
. Им отвечает собственная волновая функция
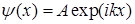 . (1.65)
. (1.65)
Ввиду непрерывности энергетического спектра нормировать (1.65) следует не на единицу, а на 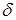 - функцию
- функцию
 . (1.66)
. (1.66)
Используя интегральное представление 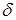 - функции
- функции
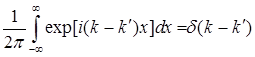 ,
,
получим для коэффициента 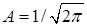 .
.
Следовательно, волновая функция свободной микрочастицы (волна де Бройля) имеет вид
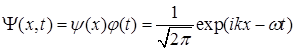 . (1.67)
. (1.67)