Микрочастица в потенциальной яме
Сделаем предварительно замечание: непрерывность производной от волновой функции не имеет места, если за некоторой поверхностью потенциальная энергия обращается в бесконечность. В эту область частица не может проникнуть, то есть на границе  .
.
Потенциальное поле  при
при 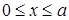 и
и 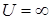 при
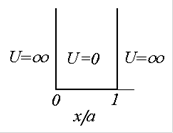
при 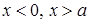 называется бесконечно глубокой потенциальной ямой (рис.1.5). Частица, которая находится в такой яме, будет все время с ней связана. Движение частицы в пространстве ограничивается областью ямы и за ее пределы частица выйти не может, то есть на границах ямы
называется бесконечно глубокой потенциальной ямой (рис.1.5). Частица, которая находится в такой яме, будет все время с ней связана. Движение частицы в пространстве ограничивается областью ямы и за ее пределы частица выйти не может, то есть на границах ямы
 . (1.109)
. (1.109)
Отражение от стенок ямы приводит к периодичности движения частицы во времени, что в свою очередь приводит к наложению условий квантования на импульс и энергию частицы. Определим волновые функции (возможные квантовые состояния) и энергетический спектр частицы. Для этого решим уравнение Шредингера (1.48) при соответствующих граничных условиях (1.109):
 . (1.110)
. (1.110)
Решение запишем в виде
 . (1.111)
. (1.111)
Используя (1.109) на границе  , получим
, получим  , и, следовательно,
, и, следовательно,
 . (1.112)
. (1.112)
Применяя граничное условие (1.109) при  , получим
, получим
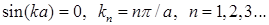 . (1.113)
. (1.113)
Число  называется квантовым числом.
называется квантовым числом.
Коэффициент  определим из условия нормировки (1.6):
определим из условия нормировки (1.6):
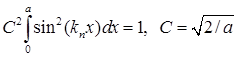 . (1.114)
. (1.114)
Таким образом, решение возможно не для любых значений 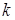 , а только для вполне определенных, которые связаны с собственными значениями энергии соотношением
, а только для вполне определенных, которые связаны с собственными значениями энергии соотношением
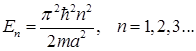 . (1.115)
. (1.115)
Этим значениям отвечает собственная волновая функция
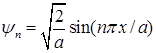 . (1.116)
. (1.116)
Энергетический спектр частицы в потенциальной яме является дискретным. Состояние с наименьшей энергией ( ) называют основным, все другие – возбужденными.
) называют основным, все другие – возбужденными.
Расстояние между соседними энергетическими уровнями в абсолютных единицах растет с увеличением квантового числа 
 , (1.117)
, (1.117)
но относительное расстояние между уровнями уменьшается
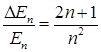 . (1.118)
. (1.118)
Для ямы макроскопических размеров (например, 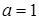 см) дискретность даже для электронов будет проявляться слабо
см) дискретность даже для электронов будет проявляться слабо
 эВ.
эВ.
Уровни располагаются вблизи друг друга и образуют квазинепрерывную полосу. Дискретная природа спектра электрона проявляется только для ямы атомного размера. Например, для ямы с 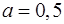 нм расстояние между соседними уровнями
нм расстояние между соседними уровнями
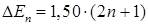 эВ.
эВ.
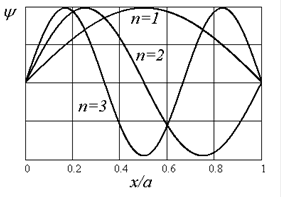
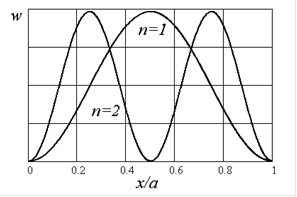
Волновые функции частицы в потенциальной яме представляют собой стоячие волны. Как легко убедиться, все функции взаимно ортогональны. Распределение плотности вероятности положения частицы в яме определяется выражением
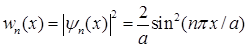 . (1.119)
. (1.119)
Соответствующие кривые для некоторых состояний приведены на рис.1.5.
Рассмотрим трехмерный случай. Потенциальная яма имеет вид прямоугольного параллелепипеда со сторонами  . Потенциальная энергия внутри ящика равняется нулю, а вне – обращается в бесконечность (непроницаемые стенки).
. Потенциальная энергия внутри ящика равняется нулю, а вне – обращается в бесконечность (непроницаемые стенки).
Компоненты поступательного движения частицы вдоль координатных осей независимы. Поэтому решение можно искать в виде функции с разделяющимися переменными
 , (1.120)
, (1.120)
что отвечает вероятности сложного события. Подставив (1.120) в (1.48) и выполнив соответствующие преобразования, получим
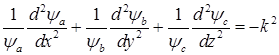 , (1.121)
, (1.121)
где
 .
.
Левая часть (1.121) разделилась на три независимых слагаемых, а правая часть является постоянной. Это возможно в том случае, когда каждое из слагаемых в левой части постоянно. Таким образом, исходное уравнение распадается на три независимых уравнения. Воспользовавшись полученным ранее решением (1.116), запишем для потенциального ящика
 . (1.122)
. (1.122)
Возможные значения энергии частицы определяются выражением
 , (1.123)
, (1.123)
где 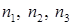 – целые числа.
– целые числа.
Если ящик кубической формы ( ), то
), то
 . (1.124)
. (1.124)
| 
|
| а | б |
| 
|
| в | г |
| Рис.1.5 Бесконечно глубокая потенциальная яма (а), волновые функции (б) и распределение густоты вероятности (в, г) |
Из (1.124) видно, что для возбужденных состояний (когда хотя бы одно из возможных значений квантовых чисел 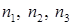 больше единицы) одному и тому же значению энергии отвечают различные волновые функции. Например, для
больше единицы) одному и тому же значению энергии отвечают различные волновые функции. Например, для 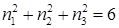 это будут
это будут  . Следовательно, такие состояния являются вырожденными. Число состояний, которые имеют одинаковые значения энергии, определяет кратность вырождения.
. Следовательно, такие состояния являются вырожденными. Число состояний, которые имеют одинаковые значения энергии, определяет кратность вырождения.