Представление произвольной функции алгебры логики в виде формулы алгебры логики
Пусть  – произвольная функция алгебры логики n переменных.
– произвольная функция алгебры логики n переменных.
Рассмотрим формулу
 (1)
(1)
которая составлена следующим образом: каждое слагаемое этой логической суммы представляет собой конъюнкцию, в которой первый член является значением функции  при некоторых определённых значениях переменных
при некоторых определённых значениях переменных  , остальные же члены конъюнкции представляют собой переменные или их отрицания. При этом под знаком отрицания находятся те и только те переменные, которые в первом члене конъюнкции имеют значение 0.
, остальные же члены конъюнкции представляют собой переменные или их отрицания. При этом под знаком отрицания находятся те и только те переменные, которые в первом члене конъюнкции имеют значение 0.
Вместе с тем формула (1) содержит в виде логических слагаемых всевозможные конъюнкции указанного вида.
Формула (1) полностью определяет функцию  . Иначе говоря, значение функции F и формулы (1) совпадают на всех наборах значений переменных
. Иначе говоря, значение функции F и формулы (1) совпадают на всех наборах значений переменных  .
.
Вид формулы (1) может быть значительно упрощён, если в ней отбросить те логические слагаемые, в которых первый член конъюнкции имеет значение 0 (и следовательно вся конъюнкция имеет значение 0). Если же в логическом слагаемом первый член конъюнкции имеет значение 1, то, пользуясь равносильностью  , этот член конъюнкции можно не выписывать.
, этот член конъюнкции можно не выписывать.
Таким образом, в результате получается формула (1), которая содержит только элементарные переменные высказывания и обладает следующими свойствами:
1. Каждое логическое слагаемое формулы содержит все переменные, входящие в функцию  .
.
2. Все логические слагаемые формулы различны.
3. Ни одно логическое слагаемое формулы не содержит одновременно переменную и её отрицание.
4. Ни одно логическое слагаемое формулы не содержит одну и ту же переменную дважды.
Перечисленные свойства будем называть свойствами совершенства или, коротко, свойствами (С).
Пусть, например, функция  имеет следующую таблицу истинности (табл. 7):
имеет следующую таблицу истинности (табл. 7):
Таблица 7

| 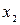
| 
| 
|
Если функция  задана таблицей истинности, то соответствующая ей формула алгебры логики может быть получена просто. Действительно, для каждого набора значений переменных, на которых функция
задана таблицей истинности, то соответствующая ей формула алгебры логики может быть получена просто. Действительно, для каждого набора значений переменных, на которых функция  принимает значение 1, запишем конъюнкцию элементарных переменных высказываний, взяв за член конъюнкции
принимает значение 1, запишем конъюнкцию элементарных переменных высказываний, взяв за член конъюнкции  , если значение
, если значение  на указанном наборе значений переменных есть 1 и отрицание
на указанном наборе значений переменных есть 1 и отрицание  , если значение
, если значение  есть 0. Дизъюнкция всех записанных конъюнкций и будет искомой формулой.
есть 0. Дизъюнкция всех записанных конъюнкций и будет искомой формулой.
Для наборов значений переменных (1,1,0), (1,0,1), (0,1,0), (0,0,0), на которых функция принимает значение 1, запишем конъюнкции  ,
,  ,
, 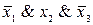 ,
,  , а искомая формула, обладающая свойствами (С), имеет вид:
, а искомая формула, обладающая свойствами (С), имеет вид:




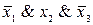

 .
.