Scheffe

Fl	N	Subset for alpha = .05

1.00		5.0000
2.00		7.0000	7.0000
3.00			9.0000
Sig.		.178	.178

Means for groups in homogeneous subsets are displayed. a Uses Harmonic Mean Sample Size = 5.000.

Результаты демонстрируют отсутствие статистически достоверных различий дисперсий 1 и 2 (Sig. = 0 ,17 8), 2 и 3(Sig. = 0 ,17 8) выборок, что убеждает в корректности парных сравнений средних значений.

ЧАСТЬ II. МЕТОДЫ СТАТИСТИЧЕСКОГО ВЫВОДА: ПРОВЕРКА ГИПОТЕЗ

МНОГОФАКТОРНЫЙ ANOVA

Многофакторный ANOVA предназначен для изучения влияния нескольких факторов (независимых переменных) на зависимую переменную и часто обозначается в соответствии с количеством факторов и числом их градаций. Например, обозначение ANOVA 3x2x2 свидетельствует о трехфакторном ANOVA (число градаций: первого фактора — 3, второго фактора — 2, третьего фактора — 2), который применяется для сравнения 12 групп (условий) (так как 3x2x2 = 12).

Принципиально этот метод не отличается от однофакторного ANOVA. Однако он позволяет оценивать не только влияние (главные эффекты) каждого фактора в отдельности, но и взаимодействие факторов: зависимость влияния одних факторов от уровней других факторов. Возможность изучать взаимодействие факторов — главное преимущество многофакторного ANOVA, которое позволяет получать зачастую наиболее интересные результаты исследования.

С целью облегчения изложения материала в качестве основного варианта многофакторного ANOVA мы сначала рассмотрим двухфакторный его вариант (2-Way ANOVA), а затем сделаем необходимые дополнения в отношении большего количества факторов.

Структура исходных данных (2-факторный ANOVA). Для каждого объекта (испытуемого) выборки измерено значение зависимой переменной (Y), а также определена его принадлежность к одной из градаций (уровней) одного фактора (Х_х) и к одной из градаций (уровней) другого фактора (Х₂). Таблица исходных данных для компьютерной обработки включает две номинативные переменные, соответствующие факторам, и одну метрическую (зависимую) переменную:

№ объектов	Х_х (Фактор I)	Х₂ (Фактор 2)	^(Зависимая переменная)





N

Модель для данных может быть представлена в виде дисперсионного комплекса ~ таблицы, строки которой соответствуют градациям (уровням) одного фактора: 1, 2, ...,/, ...,к; а столбцы — уровням другого фактора: 1, 2,...,/,..., /. Количество ячеек дисперсионного комплекса равно kxl и соответствует количеству разных групп объектов (испытуемых). Каждая ячейка с номером ij характеризуется своим сочетанием уровней факторов, численностью объектов Пу и средним значением зависимой переменной Му. Например, дисперсионный комплекс для ANOVA 2x3:

ГЛАВА 13. ДИСПЕРСИОННЫЙ АНАЛИЗ (ANOVA)

Фактор А	Фактор В

	М_п	М_п	М₁₃	м_м
	М_п	М₂₂	м_1г	м_А2
	м_п	м_т	м_ю	м

Математическая модель двухфакторного ANOVA, как и в однофакторном случае, предполагает выделение двух основных частей вариации зависимой переменной: внутригрупповой, обусловленной случайными причинами, и межгрупповой, обусловленной влиянием факторов. В межгрупповой изменчивости, в свою очередь, выделяются три ее составляющие:

□ влияние (главный эффект) 1-го фактора;

П влияние (главный эффект) 2-го фактора;

П взаимодействие факторов.

Соответственно, двухфакторный ANOVA включает в себя проверку трех гипотез: а) о главном эффекте 1-го фактора; б) о главном эффекте 2-го фактора; в) о взаимодействии факторов.

Проблема взаимодействия факторов, которая обеспечивает уникальность и незаменимость многофакторного ANOVA, заслуживает отдельного рассмотрения. Понятие взаимодействия двух независимых факторов было введено основателем дисперсионного анализа Р. Фишером для обозначения ситуации, когда влияние одного фактора на зависимую переменную проявляется по-разному на разных уровнях другого фактора.

ПРИМЕР 13.4 (Солсо Р., МакЛин М. К., с. 58-59)__________________________

Студентам колледжа предложили написать сочинение в поддержку закона о самоуправлении, противниками которого все они являлись. Испытуемым либо давали задание написать такое сочинение (условие без выбора), либо предлагали самим выбирать — писать или не писать (условие с выбором) (фактор А: 2 уровня). Кроме того, половине испытуемых в каждой из групп платили по 0,5$, а другой половине — 2,5$ за написание этого сочинения (фактор В: 2 уровня). В каждую из 4-х групп случайно отбиралось по 10 студентов. Зависимой переменной являлась степень изменения отношения студентов к закону о самоуправлении после написания сочинения. Средние значения изменения отношения для различных групп:

Фактор А	Фактор В	Средние
0,5$ (1)	2,5$ (2)
Нет выбора (1)	-0,05	+0,63	0,29
Свободный выбор (2)	+1,25	-0,07	0,59
Средние:	0,6	0,28	0,44

Результаты (рис. 13.1) демонстрируют взаимодействие факторов: размер вознаграждения (фактор В) по-разному влияет на изменение отношения — в зависимости от наличия или отсутствия свободного выбора (фактор А).

Рис. 13.1.График средних значений изменения отношения к закону о самоуправлении (к данным примера 13.4)

В условиях отсутствия выбора отношение испытуемых к закону о самоуправлении улучшилось в случае большего вознаграждения; в условиях же свободного выбора наблюдалась обратная картина: более хорошее отношение продемонстрировали те, кто получил меньшее вознаграждение.

ПРИМЕР 13.5_____________________________________________________________________

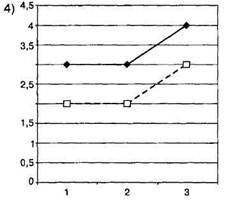
Предположим, изучается влияние на успешность группового решения задачи численности группы и наличия или отсутствия лидера в группе. Зависимая переменная — время решения задачи в минутах. Фактор А — размер группы, три градации: 1 — 2—3 человека; 2 — 5—7 человек; 3—10-15 человек. Фактор В — наличие лидера: 1 — есть; 2 — нет. В качестве объектов выступают группы. В зависимости от стиля лидерства, сложности задания и других причин, которые не учитываются, можно было бы получить разные эффекты взаимодействия факторов численности группы и наличия лидерства (рис. 13.2). График 1 демонстрирует сильное взаимодействие факторов (группы большей численности более эффективны, если в них есть лидер, а группы малой численности — при отсутствии лидера), а график 3 — более слабое взаимодействие (наличие лидера играет роль лишь в группах большой численности). Графики 2 и 4 соответствуют ситуации отсутствия взаимодействия.

ГЛАВА 13. ДИСПЕРСИОННЫЙ АНАЛИЗ (ANOVA)

Рис. 13.2. Графики средних значений успешности группового решения задачи

(к данным примера 13.5)

Приведенные примеры демонстрируют эффективность визуального анализа графиков средних значений: если линии, соответствующие разным уровням одного из факторов, не параллельны, то можно предполагать наличие взаимодействия факторов. Однако окончательное заключение об этом можно сделать только при статистическом подтверждении гипотезы о взаимодействии по результатам ANOVA. Таким образом, графики средних значений особенно полезны для интерпретации обнаруженного статистически достоверного взаимодействия факторов.

Исходные предположения многофакторного ANOVA: распределение зависимой переменной в сравниваемых генеральных совокупностях (соответствующих ячейкам дисперсионнго комплекса) характеризуется нормальным законом и одинаковыми дисперсиями. Выборки в каждой ячейке являются случайными и независимыми.

Ограничения: если выборки (ячейки) заметно различаются по численности и их дисперсии различаются статистически достоверно, то метод неприменим. Число наблюдений в каждой ячейке не должно быть меньше 2 (желательно — не менее 5). Проверка допустимости применения ANOVA сводится к про-

ЧАСТЬ П. МЕТОДЫ СТАТИСТИЧЕСКОГО ВЫВОДА: ПРОВЕРКА ГИПОТЕЗ

верке однородности дисперсии в сравниваемых выборках в случае, если они заметно различаются по численности. Для проверки однородности дисперсии применяется критерий Ливена (Levene's Test of Homogeneity ofVariances).

Дополнительно возможны множественные сравнения средних значений, позволяющие сделать вывод о том, как различаются друг от друга средние значения, соответствующие разным градациям факторов.

Общая схема двух- (и более) факторного ANOVA принципиально не отличается от однофакторного случая и определяется выделением в общей изменчивости зависимой переменной (SS_tol) ее внутригрупповой (случайной, SS_wg) и межгрупповой (факторной, SS_bg) составляющих:

SS_tot⁼ S^wg ⁺ SSfr_g.

Отличие заключается в выделении дополнительных составляющих межгрупповой (факторной) изменчивости в соответствии с проверяемыми гипотезами. Для двухфакторного случая:

SSf,g = SS_A + SS_B + SS_Ab,

где SS_A, SS_B — суммы квадратов для факторов Аи В, a SS_AB — сумма квадратов для взаимодействия факторов. Соответственно, для каждого источника изменчивости далее вычисляются степени свободы и средние квадраты, вычисляются /'-отношения для проверяемых гипотез и определяютсяр-уровни значимости.

Последовательность вычислений основных показателей для двухфакторного ANOVAрассмотрим на упрощенном примере — при равной численности сравниваемых выборок (объектов в ячейках). Для случая с неравной численностью наблюдений в ячейках логика и общая последовательность вычислений не меняются, хотя сами вычисления и становятся более громоздкими.

Фактор А	Фактор В
	2
	М_и	Ми		м_м
		м_п	м₂₃
	м_а		м_въ	м

Численность каждой ячейки равна п, общее число наблюдений — 6/7 = N.

Напомним, что двухфакторный ANOVA проверяет 3 статистические гипотезы: а) о главном эффекте фактора А (о различии М_м и М_А2); б) о главном эффекте фактора В (о различии М_т, M_m и М_вз); в) о взаимодействии факторов Аи В (влияние фактора А различается для разных уровней фактора В, и наоборот).

Межгрупповая (SS_bg) и внутригрупповая (SS^) суммы квадратов вычисляются как составные части общей суммы квадратов (SS_lot):

ГЛАВА 13. ДИСПЕРСИОННЫЙ АНАЛИЗ (ANOVA)

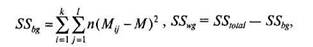
где к — число уровней фактора А; I — число уровней фактора В; М_о — среднее значение для ячейки ij.

Отношение межгрупповой и общей суммы квадратов — коэффициент детерминации. Как и в однофакторном случае, он показывает долю общей дисперсии зависимой переменной, которая обусловлена совокупным влиянием факторов (факторной моделью):

Чем больше этот показатель, тем больше общая дисперсия зависимой переменной объясняется влиянием изучаемых факторов. Межгрупповая сумма квадратов состоит из трех составляющих ее сумм квадратов: для фактора А, для фактора В, для взаимодействия факторов Аи В: