УРАВНЕНИЕ ПАУЛИ
Будем искать оператор 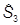 в виде
в виде
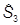 =аa1a2 .
=аa1a2 .
При коммутации с 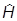 его член bmc2 даст нуль, ибо b антикоммутирует с a1 и a2, а значит, коммутирует с их произведением. Поэтому
его член bmc2 даст нуль, ибо b антикоммутирует с a1 и a2, а значит, коммутирует с их произведением. Поэтому
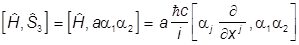 .
.
Используя перестановочные соотношения для aj , найдем
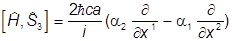 .
.
Сравнивая с нужным результатом, найдем а = -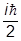 , и потому
, и потому
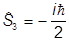 a1a2.
a1a2.
Учитываем явный вид матриц aj :
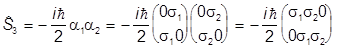 ,
,
а также то, что s1s2=is3 :
 .
.
Аналогично вычисляются 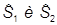 :
:
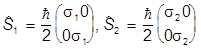 .
.
Оператор квадрата спина есть
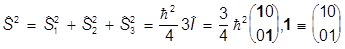 ,
,
так как s2j=1. Таким образом,
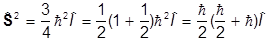 .
.
С другой стороны, из перестановочных соотношений для операторов момента мы в свое время получали
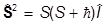 ,
,
где S-значение спинового момента. Сравнивая с 3/4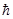 2, находим
2, находим
S = 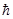 /2,
/2,
т.е. уравнение Дирака описывает частицы со спином 1/2 (электрон, позитрон, мюон, протон, нейтрон и т.д.). Для описания нейтрино, у которых тоже S= 1/2, уравнение Дирака нужно модифицировать, так как у них m = 0.
Вернемся к уравнению Клейна-Гордона - релятивистскому уравнению второго порядка, которому должна подчиняться любая волновая функция. Из него было ранее получено уравнение непрерывности
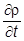 + divj= 0,
+ divj= 0,
где
r = 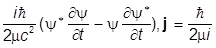 {y*(Ñy)-(Ñy*)y},
{y*(Ñy)-(Ñy*)y},
причем величина r не является положительно определенной и не может поэтому быть интерпретирована как плотность вероятности. Но, рассматривая уравнение Дирака, мы перешли от r и j к rе и je - величинам, описывающим плотность зарядов и токов. Это означает, что в релятивистских уравнениях нужно отказаться от точного описания одночастичных систем, а считать, что они описывают как-то системы многих частиц. Итак, делаем переходы
r ® re = er, j® je = ej
Так как e=const, то re и je также удовлетворяют уравнению непрерывности
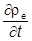 + divje = 0,
+ divje = 0,
которое теперь выражает закон сохранения электрического заряда. Так как
Е = ±eр , eр 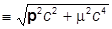 ,
,
то в любой релятивистской теории возникают решения с положительными и отрицательными энергиями
y+: E = eр , y-: E = -eр.
Им отвечают плотности заряда
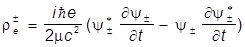 .
.
Рассмотрим нерелятивистский предел этих выражений. Так как y± удовлетворяют уравнению Клейна-Гордона, то для них
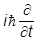 y ® Ey, -
y ® Ey, -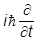 y* ® Ey*
y* ® Ey*
(см. самое начало релятивистских рассмотрений). Подстановка дает
re± = e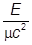 y±*y±.
y±*y±.
Нерелятивистский предел-это r2<< m2c2, или eр»mc2.
1. При Е=eр получаем Е » mc2, и
rе+ = еy+*y+.
Это есть положительно определенная величина. При нормированной функции y+ интеграл от нее будет равен е, а значит rе можно интерпретировать как плотность заряда одной частицы с q=e. В многочастичной системе rе+ - это плотность зарядов, описываемых функцией y+.
2. При Е = -eр получаем Е » -mc2 , и
rе- = -еy-*y-.
Это есть плотность зарядов для частиц с q = -е.
Таким образом, в нерелятивистском приближении решения УКГ с положительной и отрицательной энергиями задают плотность вероятности обнаружения частиц и античастиц, соответственно.
Найдем спин частиц, описываемых УКГ. Убедимся, что орбитальный момент для этих частиц сохраняется, т.е. его оператор коммутирует с гамильтонианом. Этот оператор
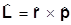
в импульсном представлении записывается как
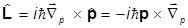 ,
,
откуда, в частности,
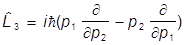 .
.
Записываем уравнение на собственные значения гамильтониана в импульсном представлении:
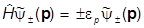
и рассматриваем коммутатор на его решениях:
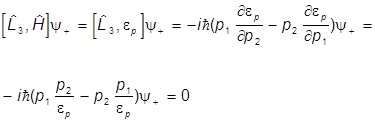
Аналогично получаем, что
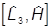 y- = 0.
y- = 0.
Таким образом, оператор орбитального момента сохраняется, и его можно считать полным моментом. Поэтому УКГ описывает частицы с нулевым спином: S=0.
Примечание. Показано только для 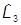 , но совершенно аналогично доказывается, что
, но совершенно аналогично доказывается, что 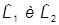 тоже коммутируют с
тоже коммутируют с 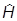 . Тем не менее, отсюда строго говоря, не следует, что S=0. Мы доказали только, что
. Тем не менее, отсюда строго говоря, не следует, что S=0. Мы доказали только, что 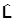 коммутирует с
коммутирует с 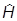 , и отсюда следует только то, что и
, и отсюда следует только то, что и 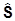 коммутирует с
коммутирует с 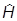 , так как в силу изотропии пространства
, так как в силу изотропии пространства 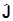 коммутирует с
коммутирует с 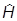 всегда. Значит, по ходу дела совершено предположение, что
всегда. Значит, по ходу дела совершено предположение, что 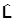 =
=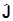 , но оно-то ниоткуда не следует. Тем не менее, все можно обосновать и абсолютно строго. Мы доказали только то, что УКГ может описывать частицы с S=0.
, но оно-то ниоткуда не следует. Тем не менее, все можно обосновать и абсолютно строго. Мы доказали только то, что УКГ может описывать частицы с S=0.
Так или иначе, принимаем, что УКГ описывает частицы с нулевым спином - например, пионы, каоны.
Вернемся вновь к уравнению Дирака и введем в рассмотрение взаимодействие частиц с внешним электромагнитным полем. Оно описывается 4-потенциалом
Аm = {А0,А1,А2,А3} = {j,-А},
и по общему правилу нужно от обычного 4-импульса перейти к обобщенному 4-импульсу
pm ® pm - 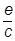 Аm,
Аm,
что в трехмерных обозначениях сводится к известным заменам
Е ® Е - еj, p® p -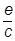 А.
А.
В операторном виде
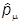 ®
® 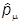 -
-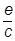
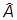 m,,
m,,
и уравнение Дирака превращается в следующее:
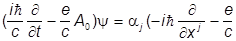 Aj)y + bmcy.
Aj)y + bmcy.
Желаем выяснить, во что переходит это полное уравнение Дирака в нерелятивистском пределе. Нас интересуют стационарные состояния, а потому ищем решения в виде
y(r,t) = 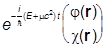 .
.
Сама функция y-4 - компонентный столбец, а записанные функции j и c - двухкомпонентные столбцы:
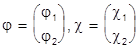
(см. выше). В искомой волновой функции Е+mc2 - полная энергия, а mc2 - энергия покоя, значит Е-«просто» энергия, как раз и имеющая непосредственный релятивистский аналог. Подставляем написанное 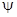 в полное уравнение Дирака, и получаем
в полное уравнение Дирака, и получаем
(Е - еА0)j = Cs (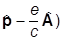 c
c
(Е + 2mc2 - еА0)c = Cs (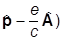 j.
j.
Пока все точно. Теперь рассматриваем нерелятивистское приближение, в котором êЕ ê<<mc2, причем считаем поле слабым - в том смысле, что êеА0ê<<mc2. Из второго уравнения системы выражаем c через j и делаем указанные приближения:
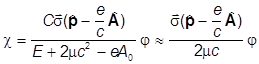 .
.
Видим, что в нерелятивистском пределе c мала: c » v/c×j. Подставляем эту функцию в первое уравнение системы:
(Е-еА0)j = 1/2m [s ( 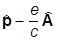 )]2j.
)]2j.
Теперь начинаем преобразовывать с учетом того, что
si2 = 1, sisj = ieijk ( i ¹ j).
Имеем
[s (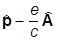 )]2 =
)]2 = 
=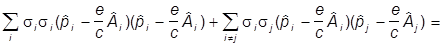
=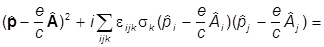
= 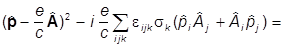
= 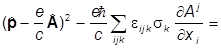
= 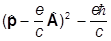 s
s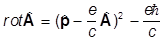 (s,H)
(s,H)
где H -напряженность магнитного поля. Переход к предпоследней строке осуществляется так:
= - 
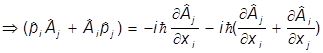 ,
,
но второй член симметричен по индексам i и j, и его свертка с антисимметричным тензором eijk дает нуль. При переходе к последней строке учтено, что в тензорной символике ротор определяется так:
(rota)k = eijk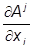
После этих выкладок самое верхнее на странице уравнение можно переписать так:
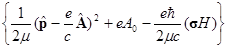 j = Ej.
j = Ej.
Это есть что-то вроде стационарного уравнения Шредингера для дираковской частицы со спином S=1/2 (электрона) в электромагнитном поле, причем в нерелятивистском приближении. Оно называется уравнением Паули. Слева стоит полный гамильтониан, содержащий три члена. Первый отвечает кинетической энергии частицы и взаимодействию ее орбитального момента с внешним магнитным полем. Второй член - энергия частицы в электрическом поле. Третий член следует интерпретировать как взаимодействие собственного (спинового) магнитного момента частицы с внешним магнитным полем. Имея в виду, что в электродинамике энергия взаимодействия магнитного момента с магнитным полем есть
- (mH) ,
как раз и естественно отождествить величину
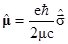
с собственным магнитным моментом. Тогда уравнение Паули запишется как
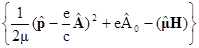 j=Ej.
j=Ej.
Таким образом, у электрона есть некий врожденный магнитный момент, не зависящий от состояния его движения. Его можно записать как
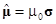 ,
,
где
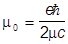
есть магнетон Бора. Вспоминая, что оператор спина 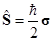 , найдем
, найдем
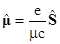 ,
,
а для орбитального движения
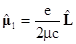 .
.
Отношение магнитного момента к механическому называется гиромагнитным отношением. Видим, что для спинового магнетизма он вдвое больше, чем для орбитального. Выбирая ось z вдоль поля, запишем для магнитной энергии
- ( .
.
Так как Sz = 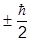 , то вклад в энергию будет таким:
, то вклад в энергию будет таким:
± m0H = ±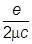 H.
H.
Для электрона, позитрона и мюонов получается значение собственного момента очень хорошо согласующееся с опытом. Правда, отклонение все-таки есть, но оно составляет около 0,1% и полностью объясняется квантовой электродинамикой («аномальный» магнитный момент возникает за счет вакуумных поправок). При обсуждении свойств нуклонов вводится ядерный магнетон
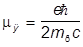 .
.
Если бы протон и нейтрон описывались уравнением Дирака, то получалось бы
mр = mя, mп =0.
Эксперимент же дает
mр @ 2,79mя, mп @-1,91mя.
Эти расхождения происходят из-за того, что для нуклонов приближение свободных частиц неверно с самого начала: они участвуют в очень интенсивном сильном взаимодействии, которое следует как-то сразу учитывать. Так, из-за этого взаимодействия каждый «голый» нуклон оказывается окруженным пионной «шубой», которая и портит затравочные магнитные моменты. На самом деле это старая точка зрения. Все дело в том, что нуклоны состоят из кварков, у которых тоже есть магнитные моменты. Вот из них-то и складываются магнитные моменты протона и нейтрона, и здесь все получается более или менее хорошо. Для нуклонов можно использовать уравнение Паули, но в него нужно включать экспериментальные значения магнитных моментов (для электрона он получился!).