рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Энергетика
- /
- Вид работы: Курсовые Работы
- /
- С использованием теоремы об изменении кинетической энергии механической системы
Реферат Курсовая Конспект
С использованием теоремы об изменении кинетической энергии механической системы
С использованием теоремы об изменении кинетической энергии механической системы - Курсовая Работа, раздел Энергетика, Часть I. Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии системы Изобразим Расчетную Схему (Рис. 2) Рис. 2....
Изобразим расчетную схему (рис. 2)
Рис. 2. Расчетная схема
На рис. 2 обозначено:
Р1,Р2,Р3 ,Р4 – силы тяжести,
N4 – нормальные реакции опорной плоскости,
Fуп – упругая реакция пружины,
Х3, У3 – реакции подшипника блока 3,
R=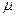 V – сила вязкого сопротивления,
V – сила вязкого сопротивления, 
F(t) – возмущающая сила.
Рассматриваемая механическая система имеет одну степень свободы (нити нерастяжимые, качение катка 3 происходит без скольжения). Будем определять ее положение с помощью координаты S. Начало отсчета координаты совместим с положением статического равновесия центра масс груза 1.
Для построения дифференциального уравнения движения системы используем теорему об изменении кинетической энергии механической системы в форме:
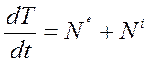 , (1.1)
, (1.1)
где Т - кинетическая энергия системы,
 - сумма мощностей внешних сил,
- сумма мощностей внешних сил,
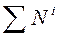 - сумма мощностей внутренних сил.
- сумма мощностей внутренних сил.
Теорема (1.1) формулируется так: "Производная по времени от кинетической энергии механической системы равна алгебраической сумме мощностей внешних и внутренних сил, действующих на точки механической системы".
Вычислим кинетическую энергию системы как сумму кинетических энергий тел 1-3:
Т=Т1+Т2+Т3 +Т4. (1.2)
Груз 1 совершает поступательное движение. Его кинетическая энергия равна:
Т1= (1.3)
(1.3)
Каток 2 совершает плоскопараллельное движение, поэтому его кинетическая энергия определяется по теореме Кенига
T2= +
+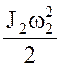 , (1.4)
, (1.4)
где V2 – скорость катка 2
JO2 - момент инерции относительно центральной оси блока;
 - угловая скорость блока.
- угловая скорость блока.
Блок 3 совершает вращательное движение около неподвижной оси. Его кинетическая энергия
T3= , (1.5)
, (1.5)
где J3 - момент инерции относительно центральной оси катка,
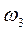 - угловая скорость катка.
- угловая скорость катка.
Блок 4 совершает плоское движение.
T= ,
,
где m4 – масса блока 4,
V4 – скорость блока 4
Кинетическая энергия всего механизма будет равна:
T=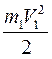 +
+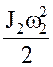 +
+ +
+  (1.6)
(1.6)
Выразим V3, V4,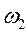 ,
, 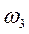 , J2, J3 через скорость груза 1.
, J2, J3 через скорость груза 1.
Положив V1=V=V2, получим
J3=m3i32, J2= ,
,  ,V4=
,V4=

 ,
,  , (1.7)
, (1.7)
Подставляя (1.3), (1.4), (1.5) в (1.6) с учетом (1.7), получаем:
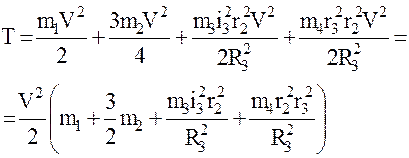 (1.8)
(1.8)
или
T= , (1.9)
, (1.9)
где mпр= =3,68 кг (1.10)
=3,68 кг (1.10)
Величину mпр=const будем называть приведенной массой. Найдем производную от кинетической энергии по времени
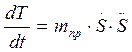 (1.11)
(1.11)
Теперь вычислим правую часть уравнения (1.1) - сумму мощностей внешних и внутренних сил.
Мощность силы равна скалярному произведению вектора силы на скорость точки ее приложения
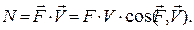 (1.12)
(1.12)
Рассматриваемая нами механическая система является неизменяемой, т. е. тела, входящие в систему, недеформируемы и скорости их точек относительно друг друга равны нулю. Поэтому сумма мощностей всех внутренних сил будет равняться нулю:
 (1.13)
(1.13)
Будут равняться нулю и мощности некоторых внешних сил, приложенных в точках, скорости которых равны нулю. Как видно из расчетной схемы, таковыми являются силы


Сумма мощностей остальных сил
 (1.14)
(1.14)
или, раскрывая скалярные произведения,
 (1.15)
(1.15)
С учетом кинематических соотношений (1.7) сумму мощностей внешних сил преобразуем к виду:

 |
В состоянии покоя приведенная сила равна нулю. Полагая
 , получаем условие равновесия системы
, получаем условие равновесия системы

тогда, учитывая, что сила вязкого сопротивления 
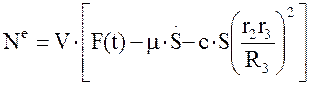 (1.16)
(1.16)
или
Ne=V Fпр , (1.17)
где
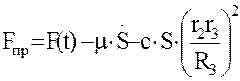 (1.18)
(1.18)
Величину Fпр будем называть приведенной силой.
Подставим выражения для производной от кинетической энергии (1.11) и сумму мощностей всех сил (1.17) с учетом (1.18) в уравнение (1.1). Тогда, получаем дифференциальное уравнение движения системы:
 (1.19)
(1.19)
Запишем последнее уравнение в виде:
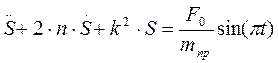 , (1.20)
, (1.20)
где введены коэффициенты, имеющие определенный физический смысл:
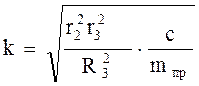 - циклическая частота свободных колебаний,
- циклическая частота свободных колебаний,
k = 3,06 с-1
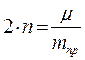 - показатель степени затухания колебаний.
- показатель степени затухания колебаний.
n = 0,14 с-1
Запишем начальные условия движения:
t=0 | 
 . (1.21)
. (1.21)
Выражения (1.20) и (1.21) совместно представляют математическую модель для решения второй задачи динамики.
– Конец работы –
Эта тема принадлежит разделу:
Часть I. Вывод дифференциального уравнения движения с использованием теоремы об изменении кинетической энергии системы
Кафедра теоретической механики... КУРСОВАЯ РАБОТА ПО РАЗДЕЛУ quot ДИНАМИКА quot ИССЛЕДОВАНИЕ КОЛЕБАНИЙ... Вариант...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: С использованием теоремы об изменении кинетической энергии механической системы
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов