рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Энергетика
- /
- III.5.1. Дипольные моменты молекул диэлектрика
Реферат Курсовая Конспект
III.5.1. Дипольные моменты молекул диэлектрика
III.5.1. Дипольные моменты молекул диэлектрика - раздел Энергетика, Электростатикое взаимодействие. Электростатикие заряды и их свойства. 1º. Вещества, Которые Не Проводят Электрического Тока, Называются Диэлек...
1º. Вещества, которые не проводят электрического тока, называются диэлектриками. При не слишком высоких температурах и в условиях, когда диэлектрики не подвержены действию очень сильных электрических полей, в этих веществах, в отличие от проводников, отсутствуют свободные носители электрического заряда.
2º. Молекулы диэлектрика электрически нейтральны и содержат равное число положительных и отрицательных зарядов. Тем не менее молекулы обладают электрическими свойствами. В первом приближении молекулу диэлектрика можно рассматривать как диполь, имеющий дипольный момент ре = ql (III.2.2.3°), где q – абсолютная величина суммарного положительного (а также суммарного отрицательного) заряда, l – расстояние между центрами тяжести положительных и отрицательных заряженных частиц. Как всякий диполь, молекула вещества создает в окружающем пространстве электрическое поле (III.2.2.3°).
3°. Диэлектрик называется неполярным (неполярный диэлектрик), если электроны атомов в его молекулах расположены симметрично относительно ядер (Н2, О2, СС14 и др.). В таких молекулах центры тяжести положительных и отрицательных зарядов совпадают в отсутствие внешнего электрического поля [l = 0 (п. 2°)] и дипольный момент ре молекулы равен нулю. Если неполярный диэлектрик помещен во внешнее электрическое поле, то происходит деформация электронных оболочек (VI.2.3.6º) в атомах (молекулах) и центры тяжести положительных и отрицательных зарядов смещаются друг относительно друга (l ≠ 0). В молекуле (атоме) диэлектрика возникает индуцированный (наведенный) дипольный электрический момент, пропорциональный напряженности Е электрического поля: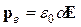 (в СИ), где α – коэффициент поляризуемости (поляризуемость) молекулы (атома), ε0 – электрическая постоянная в СИ (III.1.2.7°).
(в СИ), где α – коэффициент поляризуемости (поляризуемость) молекулы (атома), ε0 – электрическая постоянная в СИ (III.1.2.7°).
Поляризуемость молекулы зависит только от объема молекулы. Существенно, что α не зависит от температуры. Тепловое движение молекул неполярных диэлектриков не сказывается на возникновении индуцированных дипольных моментов. Молекулы с такими дипольными моментами подобны квазиупругим (индуцированным) диполям.
4°. Полярным диэлектриком называется такой диэлектрик, молекулы (атомы) которого имеют электроны, расположенные несимметрично относительно ядер атомов (Н2О, НСl, NH3, CH3Cl и др.). В таких молекулах центры тяжести положительных и отрицательных зарядов не совпадают, находясь, практически, на постоянном расстоянии l друг от друга. Молекулы полярных диэлектриков по своим электрическим свойствам подобны жестким диполям, имеющим постоянный дипольный момент: ре = const.
§ III.5.2. Поляризация диэлектриков1°. Если полярн диэлектрик (III.5.1.4°) не находится во внешн электрич поле, то в результате хаотич теплового движения молекул векторы их дипольных моментов ориентированы хаотически. Поэтому в любом физически бесконечно малом объеме ΔV*) сумма дипольных моментов всех молекул равна нулю. В неполярном диэлектрике, не находящемся во внешнем электрическом поле, вообще не могут возникнуть дипольные индуцированные моменты молекул (III.5.1.3°).
2°. При внесении диэлектрика во внешнее электрическое поле происходит поляризация диэлектрика, состоящая в том, что в любом элементарном объеме ΔV суммарный дипольный момент молекул становится отличным от нуля. Диэлектрик, который находится в таком состоянии, называется поляризованным (поляризованный диэлектрик). В зависимости от строения молекул (атомов) диэлектрика различается три типа поляризации:
а) ориентационная поляризация в полярных диэлектриках (III.5.1.4°). Внешнее электрическое поле стремится ориентировать дипольные моменты жестких диполей вдоль направления вектора напряженности электрического поля (III.5.1.5°). Этому препятствует хаотическое тепловое движение молекул, стремящееся произвольно «разбросать» диполи. В итоге совместного действия поля и теплового движения возникает преимущественная ориентация дипольных электрических моментов вдоль поля, возрастающая с увеличением напряженности электрического поля и с уменьшением температуры;
б) электронная (деформационная) поляризация в неполярных диэлектриках (III.5.1.3º). Под действием внешнего электрического поля в молекулах диэлектриков этого типа наводятся индуцированные дипольные моменты (III.5.1.3°), направленные вдоль поля. Тепловое движение молекул не оказывает влияния на электронную поляризацию. В газообразных и жидких диэлектриках практически одновременно с ориентационной происходит и электронная поляризация;
в) ионная поля-ия в твердых диэлектриках, имеющих ионные кристаллич решетки (VII.1.1.3°). (Например, NaCl, CsCl и др.). Внешнее электрическое поле вызывает смещения всех положительных ионов в направлении вектора напряженности Е, а всех отрицательных ионов – в противоположную сторону.
3°. Количественной мерой поляризации диэлектрика является вектор поляризации Ре. Вектором поляризации называется отношение электрического дипольного момента малого объема ΔV диэлектрика к величине этого объема:
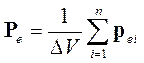 ,где Pei – электрический дипольн момент i-й молекулы, n – общее число молекул в объеме ΔV. Этот объем должен быть настолько малым, чтоб внутри него электрич поле можно было считать однородным. Одновремен число п молекул в объеме ΔV должно быть достаточно велико, чтобы можно было применять статистическ методы исследования
,где Pei – электрический дипольн момент i-й молекулы, n – общее число молекул в объеме ΔV. Этот объем должен быть настолько малым, чтоб внутри него электрич поле можно было считать однородным. Одновремен число п молекул в объеме ΔV должно быть достаточно велико, чтобы можно было применять статистическ методы исследования
4°. Для однородного неполярного диэлектрика (III.5.1.3°), находящегося в однородном электрическом поле, ,где n0 – число молекул в единице объема, ре – дипольный момент одной молекулы. Используя формулу для Ре, получим:
,где n0 – число молекул в единице объема, ре – дипольный момент одной молекулы. Используя формулу для Ре, получим: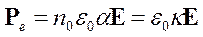 (в СИ),где κ = п0α – диэлектрическая восприимчивость вещества.
(в СИ),где κ = п0α – диэлектрическая восприимчивость вещества.
9. Теорема Гаусса для Эл поля в диэлектриках. Эл-е смещение. Диэл-я. проницаемость.
Выделим в диэлектрике замкнутую гауссову поверхность (рис. 5.9). При однородной поляризации диэлектрика на его поверхности возникнут связанные заряды, но внутри поверхности объёмных поляризационных зарядов не будет.
Рис. 5.9.
 Ситуация меняется в случае неоднородной поляризации диэлектрика, которую мы здесь не рассматриваем.
Ситуация меняется в случае неоднородной поляризации диэлектрика, которую мы здесь не рассматриваем.
 Вычислим заряд, покидающий выделенный объём через гауссову поверхность в результате поляризации (рис. 5.10):
Вычислим заряд, покидающий выделенный объём через гауссову поверхность в результате поляризации (рис. 5.10): 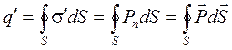 ,где s’ — локальная поверхностная плотность поляризационных зарядов, возникших на выделенной поверхности dS. Рис. 5.10.
,где s’ — локальная поверхностная плотность поляризационных зарядов, возникших на выделенной поверхности dS. Рис. 5.10.
q’ — заряд, покинувший объём.
Тогда внутри гауссовой поверхности возникнет поляризационный заряд: 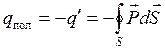 . (5.14)
. (5.14)
Сформулируем теперь теорему Остроградского-Гаусса:
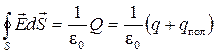 . (5.15)
. (5.15)
Заряд, определяющий поток вектора напряжённости через гауссову поверхность, в случае диэлектрика складывается из «стороннего» заряда q и заряда qпол, возникшего в объёме в результате поляризации диэлектрика.
Воспользуемся результатом (5.14) и перепишем (5.15) ещё раз:
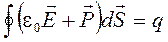
Здесь  (см. 5.10) — вектор электрического смещения. Значит, теорему Остроградского-Гаусса для электрического поля в диэлектрике можно сформулировать так:
(см. 5.10) — вектор электрического смещения. Значит, теорему Остроградского-Гаусса для электрического поля в диэлектрике можно сформулировать так: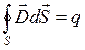 . (5.16)
. (5.16)
Поток вектора электрического смещения через любую замкнутую поверхность равен алгебраической сумме несвязанных (свободных) зарядов, заключённых внутри этой поверхности.
Ещё раз напомним, что вектор электрического смещения (индукции) связан с вектором напряжённости электрического поля (5.12): .
.
Преимущество теоремы Остроградского-Гаусса в форме (5.16) состоит в том, что теперь для расчёта потока не нужно знать величину поляризационных зарядов qпол, возникающих в диэлектрике. Поток вектора электрической индукции определяется только суммой свободных зарядов q.
10. Условия на границе раздела диэлектриков.
Рассмотрим границу двух диэлектриков с проницаемостями e1 и e2 соответственно (рис. 5.11.).
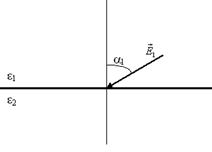 Рис. 5.11.
Рис. 5.11.
Напряжённость электрического поля в первой среде —  . Направление этого вектора задано углом a1 относительно нормали к границе раздела сред.
. Направление этого вектора задано углом a1 относительно нормали к границе раздела сред.
Определим величину и направление поля во второй среде — 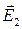 .
.
 1. Воспользуемся теоремой о циркуляции электрического поля:
1. Воспользуемся теоремой о циркуляции электрического поля:
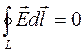 .
.
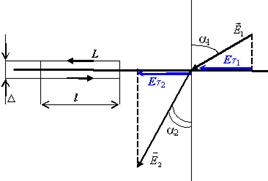
Выберем на границе раздела сред замкнутый прямоугольный контур длины l и ширины D (рис. 5.12.). Частично этот контур проходит в первой среде, а частично — во второй. Циркуляция вектора напряжённости электрического поля по этому контуру равна нулю.
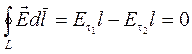 .
.
Здесь мы учли, что вклад в циркуляцию участков D стремится к нулю, при стремящейся к нулю ширине контура D. Отсюда следует, что: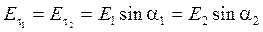 .(5.17)
.(5.17)
При переходе через границу раздела сред, касательная составляющая вектора напряжённости не меняется.
 Для того чтобы выяснить, как меняется нормальная составляющая вектора напряжённости на границе сред, воспользуемся теоремой Остроградского-Гаусса (рис. 5.13.). Выберем на границе сред замкнутую цилиндрическую поверхность высоты h и с основаниями S1 = S2 = S, лежащими по разные стороны границы раздела диэлектриков. Рис. 5.12.
Для того чтобы выяснить, как меняется нормальная составляющая вектора напряжённости на границе сред, воспользуемся теоремой Остроградского-Гаусса (рис. 5.13.). Выберем на границе сред замкнутую цилиндрическую поверхность высоты h и с основаниями S1 = S2 = S, лежащими по разные стороны границы раздела диэлектриков. Рис. 5.12.
Согласно теореме Остроградского-Гаусса: . Рис. 5.13.
. Рис. 5.13.
Но по условию свободные заряды на границе раздела сред отсутствуют: qсвободн = 0, поэтому: .Устремляя высоту цилиндра h к нулю, придём к выводу, что к нулю будет стремиться и поток вектора электрической индукции через боковую поверхность цилиндра. Искомый поток будет складываться только из потоков через основания:
.Устремляя высоту цилиндра h к нулю, придём к выводу, что к нулю будет стремиться и поток вектора электрической индукции через боковую поверхность цилиндра. Искомый поток будет складываться только из потоков через основания:
 ;
;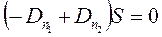 ;
; . Но D = ee0E. Следовательно:
. Но D = ee0E. Следовательно: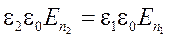 .
.
Таким образом, нормальная составляющая вектора напряжённости электрического поля во второй среде равна: 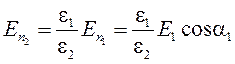 (5.18) Теперь, зная составляющие вектора
(5.18) Теперь, зная составляющие вектора :(5.17):
:(5.17): 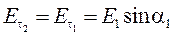 ,
,
(5.18): нетрудно найти и сам вектор:
нетрудно найти и сам вектор: .
.
Угол a2, который вектор напряжённости поля образует во второй среде с нормалью к границе раздела диэлектриков, найдём, разделив уравнения (5.17) и (5.18): 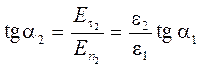 (5.19)
(5.19)
Уравнение (5.19) представляет собой закон преломления линий напряжённости электрического поля на границе раздела двух диэлектрических сред.
11.Электростатич поле шара,цилиндра,плоской пластины,заряженных по объему
Электростатическое поле шара. Пусть имеем шар радиуса R, равномерно заряженный с объемной плотностью . 
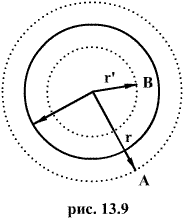
В любой точке А, лежащей вне шара на расстоянии r от его центра (r>R), его поле аналогично полю точечного заряда  , расположенного в центре шара. Тогда вне шара
, расположенного в центре шара. Тогда вне шара 
а на его поверхности (r=R) 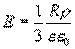
В точке В, лежащей внутри шара на расстояний r от его центра (r>R), поле определяется лишь зарядом 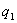 , заключенным внутри сферы радиусом r. Поток вектора напряженности через эту сферу равен
, заключенным внутри сферы радиусом r. Поток вектора напряженности через эту сферу равен

с другой стороны, в соответствии с теоремой Гаусса

Из сопоставления последних выражений следует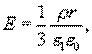
где - диэлектрическая проницаемость внутри шара. Зависимость напряженности поля, создаваемого заряженной сферой, от расстояния до центра шара приведена на (рис.13.10)
- диэлектрическая проницаемость внутри шара. Зависимость напряженности поля, создаваемого заряженной сферой, от расстояния до центра шара приведена на (рис.13.10)

Вычисление поля однородно заряженного цилиндра. OO' – ось симметрии. При r ≥ R весь поток вектора напряженности будет проходить через боковую поверхность цилиндра, площадь которой равна 2πrl, так как поток через оба основания равен нулю. Применение теоремы Гаусса дает:
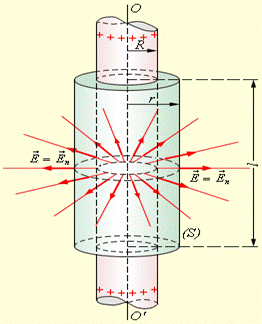
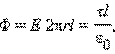
где τ – заряд единицы длины цилиндра. Отсюда

Этот результат не зависит от радиуса R заряженного цилиндра, поэтому он применим и к полю длинной однородно заряженной нити.
Для определения напряженности поля внутри заряженного цилиндра нужно построить замкнутую поверхность для случая r < R. В силу симметрии задачи поток вектора напряженности через боковую поверхность гауссова цилиндра должен быть и в этом случае равен Φ = E 2πrl. Согласно теореме Гаусса, этот поток пропорционален заряду, оказавшемуся внутри замкнутой поверхности. Этот заряд равен нулю. Отсюда следует, что электрическое поле внутри однородно заряженного длинного полого цилиндра равно нулю.
Рассмотрим еще один пример симметричного распределения зарядов – определение поля равномерно заряженной плоскости (рис. 1.3.5).
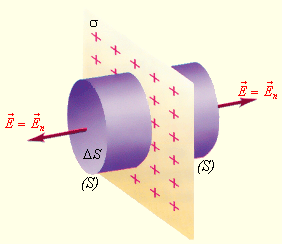 Поле равномерно заряженной плоскости. σ – поверхностная плотность заряда. S – замкнутая гауссова поверхность
Поле равномерно заряженной плоскости. σ – поверхностная плотность заряда. S – замкнутая гауссова поверхность
В этом случае гауссову поверхность S целесообразно выбрать в виде цилиндра некоторой длины, закрытого с обоих торцов. Ось цилиндра направлена перпендикулярно заряженной плоскости, а его торцы расположены на одинаковом расстоянии от нее. В силу симметрии поле равномерно заряженной плоскости должно быть везде направлено по нормали. Применение теоремы Гаусса дает: 
где σ – поверхностная плотность заряда, т. е. заряд, приходящийся на единицу площади.
Полученное выражение для электрического поля однородно заряженной плоскости применимо и в случае плоских заряженных площадок конечного размера. В этом случае расстояние от точки, в которой определяется напряженность поля, до заряженной площадки должно быть значительно меньше размеров площадки.
12. Уравнения электростатики диэлектриков.
Пусть внешнее поле создается системой неподвижных электрических зарядов. В этом случае в системе уравнений Максвелла все производные по времени обращаются в нуль. Считая, токи равными нулю, получим систему уравнений электростатики диэлектриков,
. 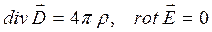
(14.10)
Здесь 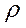 - объемная плотность сторонних зарядов,
- объемная плотность сторонних зарядов,  - макроскопическое электрическое поле,
- макроскопическое электрическое поле,
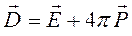 , (14.11)
, (14.11)
 . (14.12)
. (14.12)
Если поверхностная плотность сторонних зарядов принять равной нулю, то граничные условия на границе диэлектриков выглядят следующим образом:
 , (14.13)
, (14.13)
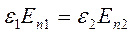 . (14.14)
. (14.14)
Электрическое поле внутри диэлектрика является потенциальным. Следовательно,
 . (14.15)
. (14.15)
В случае однородного диэлектрика,  , в котором имеются сторонние заряды с объемной плотностью
, в котором имеются сторонние заряды с объемной плотностью  , уравнение для потенциалов имеет вид:
, уравнение для потенциалов имеет вид:
 ,
,
 . (14.16)
. (14.16)
Решение данного уравнения есть:
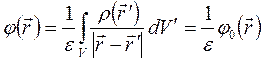 , (14.17)
, (14.17)
где 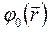 - потенциал поля, создаваемого в вакууме тем же распределением зарядов
- потенциал поля, создаваемого в вакууме тем же распределением зарядов  . Электрическое поле
. Электрическое поле
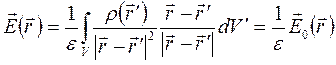 , (14.18)
, (14.18)
где 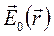 - электрическое поле в вакууме. Следовательно, потенциал поля и электрическое поле в диэлектрике ослабляются по сравнению с вакуумом в
- электрическое поле в вакууме. Следовательно, потенциал поля и электрическое поле в диэлектрике ослабляются по сравнению с вакуумом в  раз.
раз.
13. Проводники в электростатическом поле. Напряженность у поверхности
1°.В твердых металлич провод-ах сущ носители тока–свободные электроны, котор под действием внешнего электрич поля могут перемещ-ся по объему проводника. Электроны возникают, когда вещество металлич проводника переходит из менее конденсированного состояния в более конденсированное – из газообразного в жидкое или твердое. При этом происходит обобществление валентных электронов (VI.2.3.9°), которые отделяются от «своих» атомов и образуют своеобразный электронный газ.
2°.Электрич св-ва провод-ов в условиях электростатики опред-ся поведением электронов проводимости во внешнем электростатич поле. В отсутствии внешнего электростатич поля электрич поля электронов проводимости и положительных ионов металла («атомных остатков») взаимно компенсируют др др. Если металлич проводник внесен во внешнее электростатич поле, то под действ этого поля электроны проводимости перераспред-ся в проводнике таким образом, чтоб в любой точке внутри провод-ка электрич поле электронов проводимости и положит ионов скомпенсировало внешнее электростатич поле.
В любой точке внутри провод-ка, находящ-ся в электростатич поле, напряженность установивш-ся результир-го электрического поля равна нулю.
3°.На поверхности проводника вектор Е напряженности должен быть направлен по нормали к поверхности. В противн случ касательная составляющая Eτ вектора Е вызовет перемещение зарядов по поверх-ти проводника, что противоречит статическому распред-ию зарядов. Из этого результата вытекает ряд следствий:
а) внутри проводника во всех точках Е = 0; на его поверхности во всех точках Е = En (Eτ = 0), где En – нормальная составляющая вектора напряженности;
б) весь объем проводника, находящ-ся в электростатич поле, яв-ся эквипотенциальным, так как в любой точке внутри проводника

 и
и  ; в) поверх-ть проводника яв-ся эквипотенц поверхностью (III.3.3.4°), так как для любой линии на поверхности
; в) поверх-ть проводника яв-ся эквипотенц поверхностью (III.3.3.4°), так как для любой линии на поверхности

 и
и 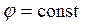 ;
; г) в заряженном проводнике некомпенсированные заряды располагаются только на поверхности. Это следует из теоремы Остроградского-Гаусса (III.2.3.3°), согласно которой суммарный заряд q, находящийся внутри проводника внутри некоторого объема, ограниченного произвольной замкнутой поверхностью S, равен:
г) в заряженном проводнике некомпенсированные заряды располагаются только на поверхности. Это следует из теоремы Остроградского-Гаусса (III.2.3.3°), согласно которой суммарный заряд q, находящийся внутри проводника внутри некоторого объема, ограниченного произвольной замкнутой поверхностью S, равен:
,так как D = 0 во всех точках поверхности.
4°.Если электростатическое поле создается заряженным проводником, то смещение и напряженность этого поля вблизи поверхности проводника вычисляются по формулам: ,
, 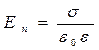 ,где n – внешняя нормаль к поверхности проводника, σ – поверхностная плотность зарядов на проводнике (III.2.2.3°), ε – относительная диэлектрическая проницаемость среды (III.1.2.4°), ε0 – электрическая постоянная в СИ (III.1.2.7º).
,где n – внешняя нормаль к поверхности проводника, σ – поверхностная плотность зарядов на проводнике (III.2.2.3°), ε – относительная диэлектрическая проницаемость среды (III.1.2.4°), ε0 – электрическая постоянная в СИ (III.1.2.7º).
14. Электроемкость уедин-го. проводника. Взаимная емкость. Конденсаторы.
1º. Если на уединен провод-ке возрастает сообщен ему заряд, то он распред-ся по поверх-ти проводника с различной поверхностн плотностью. Хаар-р распред-ия заряда зависит только от формы провод-ка, а не от заряда, кот уже имеется на провод-ке. Каждая новая порция зарядов распред-ся по поверх-ти провод-ка подобно предыдущ. Отсюда следует, что в любой точке поверх-ти провод-ка поверхностн плотность σ заряда возрастает прямо пропорцион заряду q на провод-ке: σ = kq, где k = f (x, у, z) есть функция координат рассматриваемой точки поверхности. Потенциал поля заряженного проводника 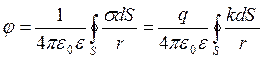 .
.
Для точек поверхности S проводника интеграл зависит только от размеров и формы поверхности, и поэтому потенциал φ проводника прямо пропорционален его заряду q.
2°. Отношение заряда q уединенного проводника к его потенциалу φ называется электрической емкостью (электроемкостью, емкостью) данного проводника:
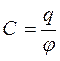 или
или  (в СИ).
(в СИ).
Электроемк уединенн провод-ка численно равна электрич заряду, кот нужно сообщить провод-ку для того, чтоб его потенциал измен-ся на единичн величину.
Электроемк уединен провод-ка завис от его формы и размеров. Для геометр-ки подобных провод-ков емкости пропорциональны их линейн размерам.
Емкость уединен провод-ка зависит от диэлектрич свойств окружающей среды. Для однородной, изотропной среды емкость провод-ка прямо пропорцион относит диэлектрич проницаемости среды.
3°. Из формулы потенциала уединенного шара радиуса следует, что емкость такого шара равна: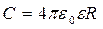 (в СИ),
(в СИ),
§ III.4.2. Взаимная емкость. Конденсаторы
1°. Если вблизи провод-ка А имеются другие провод-ки, то его электроемк больше, чем у такого же уединен провод-ка. Это объясняется тем, что когда провод-ку А сообщается заряд q, то окружающ его провод-ки заряж-ся через влияние, причем ближайшими к наводящему заряду q будут заряды противополож знака. Эти заряды, ослабляя поле, создаваемое зарядом q, снижают потенциал провод-ка и увелич его емкость.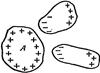 2°. Для двух близко расположенных друг от друга проводников, заряженных равными по абсолютной величине, но противоположными по знаку зарядами q, разность потенциалов φ1 – φ2, пропорциональна q:
2°. Для двух близко расположенных друг от друга проводников, заряженных равными по абсолютной величине, но противоположными по знаку зарядами q, разность потенциалов φ1 – φ2, пропорциональна q: , где C – взаимная емкость двух проводников:
, где C – взаимная емкость двух проводников: 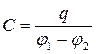 .
.
Взаимная емкость двух проводников численно равна заряду, который нужно перенести с одного проводника на другой для изменения разности потенциалов между ними на единицу.
3°. Взаимная емкость С двух провод-ов зависит от их формы, размеров и взаимн их расположения. Кроме того, С зависит от диэлектрических свойств среды, окружающей проводники. Если среда однородна и изотропна, то С прямо пропорциональна относительной диэлектрической проницаемости среды (III.1.2.4°).При удалении одного из провод-ов в бесконечность разность потенциалов φ– φ2 между ними возраст, а их взаимная емкость убыв и стремится к емкости оставшегося уединен проводника.4°. Система двух провод-ов называется конденсатором, если форма и расположение проводников обеспеч сосредоточ-е электростатич поля, созданного провод-ми, в ограничен обл простр-ва. Пров-ки, составляющ к-ор, заряжаются разноименно равными по абсолютной величине и противоположными по знаку зарядами. Сами проводники называются в этом случае обкладками конденсатора. Емкость конденсатора представляет собой взаимную емкость его обкладок.5°. Емкость плоского конденсатора, состоящего из двух параллельных металлических пластин площадью S каждая, расположенных на расстоянии d друг от друга, выражается формулой: (в СИ),где ε – относительная диэлектрич проницаем среды, заполняющ пространство между пластинами. Для плоского многопластинч к, содержащ n пластин, вместо S в формулу емкости входит S(n – 1). Формула справедлива лишь при малом d, когда можно пренебречь нарушением однородности электростатического поля у краев обкладок конденсатора.6°. Сферич к состоит из двух концентрич металлич обкладок А и В сферической формы, радиусы которых равны r1 и r2 (рис. III.4.2). Поле заряженной по поверхности сферы существует только вне сферы (III.2.1.2°). Поэтому в области между обкладками электростатич поле создается только зарядом обкладки А, а вне к-ра поля разноименно заряженных обкладок a и b взаимно уничтожаются.Емкость сферического конденсатора вычисляется по формуле:
(в СИ),где ε – относительная диэлектрич проницаем среды, заполняющ пространство между пластинами. Для плоского многопластинч к, содержащ n пластин, вместо S в формулу емкости входит S(n – 1). Формула справедлива лишь при малом d, когда можно пренебречь нарушением однородности электростатического поля у краев обкладок конденсатора.6°. Сферич к состоит из двух концентрич металлич обкладок А и В сферической формы, радиусы которых равны r1 и r2 (рис. III.4.2). Поле заряженной по поверхности сферы существует только вне сферы (III.2.1.2°). Поэтому в области между обкладками электростатич поле создается только зарядом обкладки А, а вне к-ра поля разноименно заряженных обкладок a и b взаимно уничтожаются.Емкость сферического конденсатора вычисляется по формуле: 7°. Цилиндрич к представ собой два полых коаксиальных металлич цилиндра с высотой h и радиусами r1 и r2.Формула емкости цилиндри к-ра имеет вид:
7°. Цилиндрич к представ собой два полых коаксиальных металлич цилиндра с высотой h и радиусами r1 и r2.Формула емкости цилиндри к-ра имеет вид: 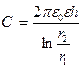 9°. Для получения больших электроемкостей исп-ся параллельное соединение к-ов, при котором соедин-ся одноименно заряженные обкладки. Общая емкость С при этом равна:
9°. Для получения больших электроемкостей исп-ся параллельное соединение к-ов, при котором соедин-ся одноименно заряженные обкладки. Общая емкость С при этом равна: ,где Ci – емкость i-го конденсатора. 10°. При последовател соединении конденсаторов они соединяются разноименно заряженными обкладками. При этом складываются величины, обратные емкостям каждого конденсатора Ci:
,где Ci – емкость i-го конденсатора. 10°. При последовател соединении конденсаторов они соединяются разноименно заряженными обкладками. При этом складываются величины, обратные емкостям каждого конденсатора Ci: 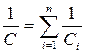 .
.
15.Емкость сферического,цилиндрич.,плоского кондеров
Поместим на внешнюю сферу (радиуса R2) заряд q, а на внутреннюю (радиуса R1) --- -q. Вычислим U --- разность потенциалов между сферами (тогда искомая емкость по определению будет равна q/U). Как известно, потенциал, создаваемый сферой вне этой самой сферы такой же, как и у точечного заряда, а внутри потенциал равен константе, такой же, как и на поверхности.
Нас будет интересовать только область между сферами.
В интересующей нас области потенциал от внешней сферы постоянен, а от внутренней потенциал на расстоянии R равен -k q/R.
(здесь k --- постоянная в законе кулона. k = 1/(4 pi Epsilon Epsilon0))
Мы хотим сосчитать разность потенциалов на сферах U = ((-kq/R) при R=R2) - ((-kq/R) при R=R1) = kq/R1-kq/R2=kq(R2-R1)/R1 R2, откуда находим, что емкость конденсатора = q/U =(1/k)*R1 R2/(R2-R1). Если подставить k, то получится ваша формула.
Для определения емкости цилиндрического конденсатора, состоящего из двух полых коаксиальных цилиндров с радиусами r1 и r2 (r2 > r1), вставленных один в другой, опять пренебрегая краевыми эффектами, считаем поле радиально-симметричным и сосредоточенным между цилиндрическими обкладками. Разность потенциалов между обкладками вычислим по формуле для поля равномерно заряженного бесконечного цилиндра с линейной плотностью t =Q/l (l≈длина обкладок). При наличии диэлектрика между обкладками разность потенциалов
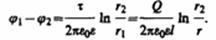 Получим выражение для емкости цилиндрического конденсатора:
Получим выражение для емкости цилиндрического конденсатора: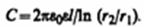
Рассмотрим две параллел проводящ пластины, расстояние между кот. мало по сравнению с их размерами. Предполож, что все силовые линии, начин-ся на одном проводнике, заканч-ся на др. Такую конструкцию называют конденсатором. Другие примеры конденсаторов - цилиндрический конденсатор, шаровой конденсатор и т.д.
Поскольку все силовые линии нач-ся и заканч-ся на электрич зарядах, отсюда следует, что заряды на обкладках конденс равны по величине и противоположны познаку.Напряженность поля между обкладками пропорциональна заряду на обкладках:q=CU.Коэффициент С-электрич емкость конденсатора.Из формулы следует, что емкость конденсатора измер-ся зарядом на каждой из обкладок, если напряжение между ними равно 1. Единица измерения - фарад. Единица емкости - это емкость такого конденсатора, у кот при изменении заряда на один Кулон напряжение между обкладками меняется на один Вольт.Емкость плоского конденсатора прямо пропорц площади обкладок и обратно пропорц расстоянию между обкладками.Кроме этого, емкость зависит от диэлектрика, заполняющего пространство между обкладками, а именно от его диэлектрической проницаемости:C/C0=e,Где C0 - емкость конденсатора, когда его обкладки находятся в вакууме, С - емкость того же конденсатора, когда между обкладками помещен диэлектрик проницаемостью e.
16. Энергия системы зарядов, конденсатора. Энергия эл-стат поля.
Энергия заряженного проводника и электрического поля
1°. Нанесение на проводник электрич заряда связано с совершением работы по преодолен кулоновского отталк-я между одноименн зарядами. Эта работа увелич электрическ энергию заряж-го провод-ка, аналогичную потенциальн энергии в механике. Работа ΔА, совершаемая при перенесении заряда dq из бесконечности на проводник, равна: ,где С и φ – электроемк и потенциал проводника. Работа, необходи для заряжения проводника от нулевого потенциала до потенциала φ,
,где С и φ – электроемк и потенциал проводника. Работа, необходи для заряжения проводника от нулевого потенциала до потенциала φ, .Соответственно, энергия заряженного уединенного проводника (собственная энергия заряженного проводника)
.Соответственно, энергия заряженного уединенного проводника (собственная энергия заряженного проводника)
 .Энергия заряженного конденсатора
.Энергия заряженного конденсатора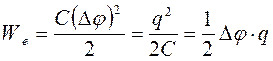 ,где С и q – электроемкость и заряд конденсатора, Δφ – разность потенциалов между противополож заряженными обкладками конд-ра. 3°. Собствен энергия заряженного провод-ка является одновремен энергией его электростатич поля. Так, для однородн электростатич поля плоского конденсатора
,где С и q – электроемкость и заряд конденсатора, Δφ – разность потенциалов между противополож заряженными обкладками конд-ра. 3°. Собствен энергия заряженного провод-ка является одновремен энергией его электростатич поля. Так, для однородн электростатич поля плоского конденсатора 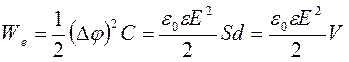 ,
,
где V = Sd – объем, в кот существует электростатич поле между обкладками конд. Энергия поля пропорцион его объему, причем энергия, заключен в единице объема, в кот сущ электростатич поле – объемная плотность энергии we – одинакова во всех точках однородного поля: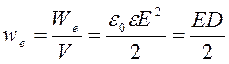 ,4°. Для неоднородных электростатических полей, создаваемых произвольными заряженными телами, объемная плотность энергии в каждой точке поля в изотропной среде выражается формулами п. 3°. Если же среда электрически анизотропна, то объемная плотность энергии электрического поля равна:
,4°. Для неоднородных электростатических полей, создаваемых произвольными заряженными телами, объемная плотность энергии в каждой точке поля в изотропной среде выражается формулами п. 3°. Если же среда электрически анизотропна, то объемная плотность энергии электрического поля равна: (в СИ), 5º. Энергия dWe бесконечно малого объема в изотропной среде, в котором существует произвольное электростатическое поле
(в СИ), 5º. Энергия dWe бесконечно малого объема в изотропной среде, в котором существует произвольное электростатическое поле
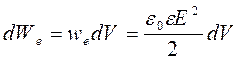 (в СИ).Полная энергия We электростатического поля
(в СИ).Полная энергия We электростатического поля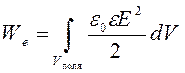 ,где интегрирование производится по всему объему поля Vполя. 6°. Полная энергия электростатического поля, создаваемого произвольным заряженным телом, равна собственной энергии этого тела
,где интегрирование производится по всему объему поля Vполя. 6°. Полная энергия электростатического поля, создаваемого произвольным заряженным телом, равна собственной энергии этого тела
 .Этот результат обобщается на случай электростатического поля, создаваемого произвольной системой зарядов. Полная энергия такой системы (III.6.1.2°) совпадает с полной энергией электростатического поля этой системы зарядов:
.Этот результат обобщается на случай электростатического поля, создаваемого произвольной системой зарядов. Полная энергия такой системы (III.6.1.2°) совпадает с полной энергией электростатического поля этой системы зарядов: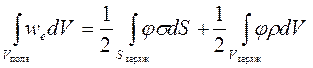 .
.
– Конец работы –
Эта тема принадлежит разделу:
Электростатикое взаимодействие. Электростатикие заряды и их свойства.
Электростатикой наз ся раздел учения об элект ве в кот изуч ся взаимод я и свойства систем эл зарядов неподвижных относит выбранной... Сущ два рода эл зарядов положит и отрицат Разноименно заряженные тела... Эл заряд любой системы тел состоит из целого числа элементар зарядов равных Кл Наименьшей по массе...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: III.5.1. Дипольные моменты молекул диэлектрика
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов