Электрический заряд. Электрическое поле. Поле точечного заряда

1. Электрический заряд. Электрическое поле. Поле точечного заряда. Суперпозиции. Распределение зарядов. Геометрическое описание электрического поля.

Электрический заряд частицы является одной из основных, первичных ее характеристик. Свойства: 1)существует в 2х видах: поло­жительный и отрицательный; 2)закон сохранения электрического заряда: в любой электрически изолированной системе алгебраиче­ская сумма зарядов не изменяется; 3)электрический заряд является релятивистски-инвариантным: его величина не зависит от системы отсчета, а значит, не зависит от того, движется он или покоится.

Электрическое поле. Взаимодействие между зарядами осуществляется через поле. Всякий электрический заряд q изменяет определенным обра­зом свойства окружающего его пространства — создает элект­рическое поле. Это поле проявляет себя в том, что помещенный в какую-либо его точку другой, «пробный», заряд испытывает действие силы

F = q'E, где вектор Е называют напряженностью электрического поля в данной точке. Вектор Е, можно определить как силу, действующую на единичный положите­льный неподвижный заряд. Проб­ный заряд q' должен быть достаточно малым, чтобы его вне­сение не вызвало заметного искажения поля (вследствие возможного перераспределения создающих поле зарядов).

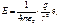Поле точечного заряда. Из опыта следует, что напряженность поля неподвижного точеч­ного заряда q на расстоянии r от него можно представить как,

где ε₀ — электрическая постоянная; е_r — орт радиуса-вектора г, проведенного из центра поля, в котором расположен заряд q, до интересующей нас точки. Здесь коэффициент 1/4πε₀= =9•10⁹м/Ф, заряд q определяют в кулонах (Кл), напряженность поля Е — в вольтах на метр (В/м). В зависимости от знака заряда q век­тор Е направлен так же, как и r, или противоположно ему. По существу формула выражает не что иное, как закон Кулона, но в «полевой» форме.

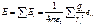Принцип суперпозиции: напряженность поля системы точечных неподвижных зарядов равна векторной сумме напряженностей полей, которые создавали бы каждый из зарядов в отдельности:

где r_i — расстояние между зарядом q_i и интересующей нас точ­кой поля.

Распределение зарядов.Для упрощения математических расчетов удобно заменить истинное распределение точечных дискретных зарядов фиктивным не­прерывным распределением.

При переходе к непрерывному распределению вводят поня­тие о плотности зарядов — объемной ρ, поверхностной σ и ли­нейной λ. По определению, ρ=dq/dV, σ=dq/dS, λ=dq/dl, где dq — заряд, заключенный соответственно в объеме dV, на поверхности dS и на длине dl. Можно представить принцип суперпозиции так:

 

Геометрическое описание электрического поля.Зная вектор Е в каждой точке, можно представить электрическое поле с помощью линий напряженности, или линий вектора Е. Эти линии проводят так, чтобы касательная к ним в каждой точке совпадала с направлением вектора Е, а густота линий, т. е. число линий, пронизывающих единичную площад­ку, перпендикулярную линиям в данной точке, была бы про­порциональна модулю вектора Е. Кроме того, этим линиям приписывают направление, совпадающее с направлением век­тора Е.

2. Поток вектора Е. Теорема Гаусса (интегральная и дифференциальная форма).

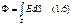Поток вектора Е.Будем считать, что густота линий Е равна модулю вектора Е. Тогда число линий, пронизывающих элементарную площадку dS, нормаль n которой составляет угол а с вектором Е, определяется согласно как Е dS cosa. Эта величина и есть поток dФ вектора Е сквозь площадку dS. В более компактной форме dФ=E_n dS=E dS, где Е_п— проекция вектора Е на нормаль n к площадке dS, dS — вектор, модуль которого равен dS, a направление совпа­дает с нормалью n к площадке. Заметим, что выбор направле­ния вектора n (а следовательно, и dS) условен, его можно было бы направить и в противоположную сторону. Если имеется некоторая произвольная поверхность S, то по­ток вектора Е сквозь нее:

Эта величина алгебраическая: она зависит не только от конфи­гурации поля Е, но и от выбора направления нормали. В случае замкнутых поверхностей принято нормаль n брать наружу об­ласти, охватываемой этими поверхностями, т. е. выбирать внешнюю нормаль.

Теорема Гаусса.поток век­тора Е сквозь замкнутую поверхность равен алгебраической сумме зарядов внутри этой поверхности, деленной на ε_о.

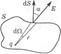Доказательство: Сначала рассмотрим поле одно­го точечного заряда q. Окружим этот заряд произвольной зам­кнутой поверхностью S и найдем поток вектора Е сквозь элемент dS:

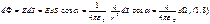
где dΩ — телесный угол, опирающийся на элемент поверхности dS, с вершиной в точке расположения заряда q. Интегрирование этого выражения по всей поверхности S эк­вивалентно интегрированию по всему телес­ному углу, т. е. заменив dΩ на 4π, полу­чим Ф = q/ε₀, как и требует формула (1.7). При более сложной форме замкнутой поверхности углы а могут быть больше π/2, а значит, cos а и dΩ в (1.8) принимают как положительные, так и отрицательные значения. Т.о, dΩ — величина алгебраическая: если dΩ опирается на внутреннюю сторону поверхности S, то dΩ> 0, если же на внешнюю сторону, то dΩ< 0.

Теперь обратимся к случаю, когда электрическое поле созда­ется системой точечных зарядов. В этом случае со­гласно принципу суперпозиции Е = e₁ + Е₂ + ..., где e₁ — поле, создаваемое зарядом q₁ и т. д. Тогда поток вектора Е можно за­писать так:

Согласно предыдущему каждый интеграл в правой части ра­вен q_i/ε₀, если заряд q_i находится внутри замкнутой поверхности S, и нулю, если снаружи поверхности S. Поэтому в правой части останется алгебраическая сумма только тех зарядов, ко­торые находятся внутри поверхности S.

Для завершения доказательства остается учесть случай, когда заряды распределены непрерывно с объемной плотностью, зависящей от координат. В этом случае можно считать, что каждый элементарный объем dV содержит «точеч­ный» заряд ρdV. Тогда в правой части (1.7):

где интегрирование проводится только по объему, заключенно­му внутри замкнутой поверхности S.

Дифференциальная форма теоремы Гаусса: представим сначала заряд q в объеме V,охватыва­емом замкнутой поверхностью S, как q_внутр = <ρ>V, где <ρ> — среднее по объему V значение объемной плотности заряда. За­тем подставим это выражение в уравнение (1.7) и разделим обе части его на V. В результате получим

 

 

Теперь устремим объем V к нулю, при этом <ρ> будет стремиться к значению ρ в данной точке поля, а значит, отношение в левой части уравнения будет стремиться к ρ/ε_о. Величину, являющуюся пределом отношения ∫ЕdS к V при V→0, называют дивергенцией поля Е и обозначают div E. Та­ким образом, по определению

 

Дивергенция является скалярной функцией координат. Выражение для дивергенции зависит от выбора системы координат. В декартовой системе координат:

Итак, при V→0 в выражении (1.15) его правая часть стремится к ρ/ε₀, а левая — к divE. Следователь­но, дивергенция поля Е связана с плотностью заряда в той же точке уравнением divE=ρ/ε₀ (Ñ·E=ρ/ε₀.) Это уравнение и выражает теорему Гаусса в дифференциаль­ной форме. вектор Е, то получим не что иное, как div E(или ÑЕ). В дифференциальной форме теорема Гаусса является лока­льной теоремой: дивергенция поля Е в данной точке зависит то­лько от плотности электрического заряда ρ в той же точке.

 

 

Теорема о циркуляции вектора Е (интегральная и дифференциальная форма). Потенциал поля точечного заряда. Потенциал поля системы зарядов. Связь между потенциалом и вектором Е. Эквипотенциальные поверхности.

Электростатическое поле является стационарным. Если в качестве пробного заряда, переносимого из точки 1 заданного поля Е в точку 2, взять единичный положительный заряд, то элементарная рабо­та сил поля на перемещении dl равна Е dl, а вся работа сил поля на пути от точки 1 до точки 2 определяется как

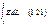
Этот интеграл берется по некоторой линии (пути), поэтому его называют линейным. Из независимости линейного интег­рала (1.21) от пути между двумя точками следует, что по про­извольному замкнутому пути этот интеграл равен нулю. Интег­рал (1.21) по замкнутому пути называют циркуляцией вектора Е и обозначают

 

Теорема о циркуляции вектора Е: циркуляция вектора Е в любом электростатическом поле равна нулю, т. е.(+д­–во)

Потенциал. Тот факт, что линейный интеграл (1.21), представляющий собой работу сил поля при перемещении единичного положите­льного заряда из точки 1 в точку 2, не зависит от пути между этими точками, позволяет утверждать, что в электрическом поле существует некоторая скалярная функция координат φ(r), убыль которой,

где φ₁ и φ₂ — значения функции φ в точках 1 и 2. Величина φ(r) называется потенциалом поля Потенциал — это величина, численно равная потенциальной энергии единичного положительного заряда в данной точке поля. Потенциалу какой-либо произвольной точки О поля можно условно приписать любое значение φ₀. Тогда потенциалы всех других точек поля определяются согласно (1.23) однозначно. Если изменить φ₀ на некоторую величину Δφ, то на такую же величину изменятся и потенциалы во всех других точках поля. Таким образом, потенциал φ определяется с точностью до произвольной аддитивной постоянной. Единицей потенциала является вольт (В).

Потенциал поля точечного заряда. Формула (1.23) справедлива не только для конечных перемеще­ний, но и для элементарных dl. Тогда согласно этой формуле элементарная убыль потенциала на этом перемещении есть –dφ=Edl(1.24)

Если известно поле Е(r), то для нахожде­ния φ надо представить Е dl как убыль некоторой функции. Эта функция и есть φ. Найдем таким способом потенциал поля неподвижного то­чечного заряда:

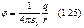
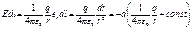где учтено, что e_rdl = 1 • (dl)_r, т.к. проекция вектора dl на век­тор е_г, а значит, и на r равна приращению модуля вектора r, т. е. dr. Величина, стоящая в круглых скобках под знаком диф­ференциала, и есть φ(r). Так как присутствующая здесь адди­тивная константа никакой физической роли не играет, ее обыч­но опускают. Т.о.:

Отсутствие в этом выражении аддитивной константы озна­чает, что мы полагаем потенциал на бесконечности (r → ∞) равным нулю.

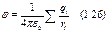Потенциал поля системы зарядов. Пусть система состоит из неподвижных точечных зарядов q₁ ,q₂,... Согласно принципу су­перпозиции в любой точке поля напряженность Е = Е₁ + Е₂ +..., где e₁ — напряженность поля заряда q₁ и т. д. Тогда мож­но записать, используя формулу (1.24): Edl=(Е₁+Е₂+...)dl=Е₁dl+ Е₂dl+...= –dφ₁–dφ₂–…= –dφ, где φ=Σφ, т. е. принцип суперпозиции оказывается справед­ливым и для потенциала. Таким образом, потенциал системы неподвижных точечных зарядов

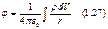r_i — расстояние от точечного заряда q_i до интересующей нас точки поля. Если заряды, образующие систему, распределены непрерыв­но, то считаем, что каждый элементарный объем dV содержит «точечный» заряд ρdV, где ρ — объемная плотность заряда в месте нахождения объема dV. С учетом это­го формуле (1.26) можно придать иной вид:

Если заряды распо­ложены только на поверхности S, то

где σ — поверхностная плотность заряда; dS — элемент поверх­ности S.

Связь между потенциалом и вектором Е.Пусть перемещение dl параллельно оси X, тогда dl = i dx, где i — орт оси X, dх — приращение координаты х, Е dl = Е i dx = Е_х dx, где Е_х — проекция вектора Е на орт i (а не на перемещение dl). Сопоставив последнее выражение с формулой (1.24), получим E_x= –∂φ/–∂x (1.29) Рассуждая аналогично, можно получить соответствующие выражения для проекций Е_у и E_z. А определив Е_х, Е_у, Е_г, легко найти и сам вектор Е:

Эквипотенциальные поверхности— поверхности, во всех точках ко­торых потенциал φ имеет одно и то же значение. Вектор Е направлен в каждой точке по нормали к эк­випотенциальной поверхности в сторону уменьшения потенци­ала φ. Вектор Е на­правлен в сторону уменьшения φ, или в сторону, противопо­ложную вектору Ñφ.