МЕТОД КОМПЕНСАЦИИ
Данный метод основан на теореме компенсации, согласно которой во всякой ЭЦ, содержащей источники и сопротивления, любое сопротивление 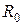 , обтекаемое током
, обтекаемое током  (рис. 5.1), может быть заменено идеальным источником, ЭДС которого по величине равна разности потенциалов на зажимах этого сопротивления и направлена против тока
(рис. 5.1), может быть заменено идеальным источником, ЭДС которого по величине равна разности потенциалов на зажимах этого сопротивления и направлена против тока  .
.

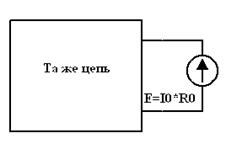
| = | 
|
| Рис. 5.1 |
Таким образом, для определения тока или напряжения в произвольном месте линейной ЭЦ в неё вводят вспомогательные компенсирующие источники, эффект от действия которых равен по величине и противоположен по знаку искомому эффекту. Вычисляя первый эффект, находим тем самым и второй. Правильность сказанного вытекает из метода наложения.
Данный метод используют тогда, когда эффект от действия вспомогательных источников можно вычислить проще, чем искомый эффект. Метод ввел Pomey в 1919 г. Из данной теоремы следует, что в тех случаях, когда в какой-либо ветви линейной ЭЦ сопротивление 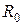 , обтекаемое током
, обтекаемое током  (рис. 5.2а), получит приращение
(рис. 5.2а), получит приращение 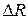 , то это вызовет в схеме приращение токов и напряжений, соответственно равные токам и напряжениям, которые вызвал бы в цепи источник ЭДС с напряжением
, то это вызовет в схеме приращение токов и напряжений, соответственно равные токам и напряжениям, которые вызвал бы в цепи источник ЭДС с напряжением 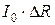 , если бы он был включен последовательно с
, если бы он был включен последовательно с 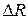 навстречу току
навстречу току  (рис. 5.2б).
(рис. 5.2б).

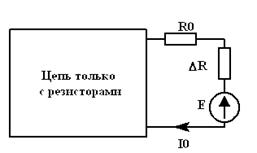
| = | 
|
| Рис. 5.2 а | Рис. 5.2 б |
Отметим, что теорема компенсации может быть использована и в случае одновременного изменения 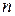 -сопротивлений цепи.
-сопротивлений цепи.
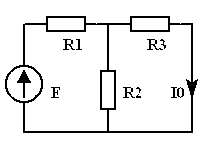
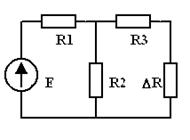
Пример: В ЭЦ (рис. 5.3а) определить какое приращение тока 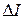 возникает в
возникает в 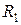 , если
, если 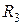 получит приращение
получит приращение 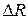 (рис. 5.3 б).
(рис. 5.3 б).
| = | 
| = | 
|
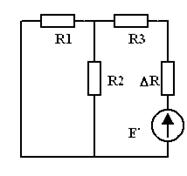
| Рис. 5.3 а | Рис. 5.3 б | Рис. 5.3 в |
|
Согласно теореме компенсации получим для расчета схему (рис. 5.3в). Используя правило деления тока, рассчитаем 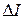 :
:
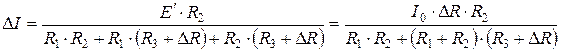 .
.
В важности теоремы компенсации можно убедиться, решая этот же пример любым другим способом, когда рассчитываются токи до и после изменения цепи с последующим их вычитанием.
Из (рис. 5.3а) по правилу деления тока получим:
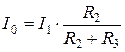 ,
, 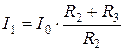 , (5.1)
, (5.1)
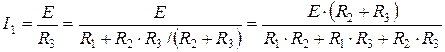 . (5.2)
. (5.2)
Из выражений (5.1) и (5.2) выделим 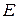 :
:
 ,
, 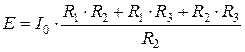 . (5.3)
. (5.3)
Рассмотрим теперь ту же схему (рис. 5.3а), в которой последовательно с 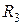 введено приращение
введено приращение 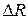 и рассчитаем изменившийся ток в сопротивлении
и рассчитаем изменившийся ток в сопротивлении 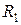 . Для этого используем выражение (5.2):
. Для этого используем выражение (5.2):
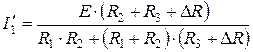 .
.
Подставим в последнем выражении вместо 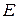 его значение из уравнения (5.3):
его значение из уравнения (5.3):
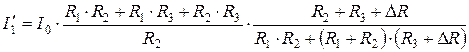 .
.
Тогда искомое приращение:
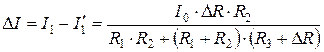 .
.
Таким образом, приведенное решение задачи оказывается более трудоемким, чем решение, получаемое с помощью теоремы компенсации.
Метод компенсации используется в теории четырехугольников, в теории сетей высокого напряжения, в теории электрических измерений.