рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Электротехника
- /
- Вид работы: Лабораторные Работы
- /
- С. 163 – 180]; [4, с. 207-212, 216-221]; [5, с. 30-34, 38-41].
Реферат Курсовая Конспект
С. 163 – 180]; [4, с. 207-212, 216-221]; [5, с. 30-34, 38-41].
С. 163 – 180]; [4, с. 207-212, 216-221]; [5, с. 30-34, 38-41]. - Лабораторная Работа, раздел Электротехника, ЭЛЕКТРОТЕХНИКА Лабораторная Работа № За Исследование Простых Цепей Синусоидаль...
Лабораторная работа № ЗА
ИССЛЕДОВАНИЕ ПРОСТЫХ ЦЕПЕЙ СИНУСОИДАЛЬНОГО ТОКА
Цель работы
Приобретение навыков работы с вольтметром, генератором, фазометром. Экспериментальная проверка законов распределения токов и напряжений в последовательной, параллельной и последовательно–параллельной цепях гармонического тока.
Основные теоретические положения
Для анализа линейных электрических цепей в установившемся синусоидальном режиме широко используется метод комплексных амплитуд (символический метод). В этом методе оперируют не реальными гармоническими напряжениями и токами, а их комплексными амплитудами:
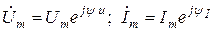 (3.1)
(3.1)
или комплексными напряжениями и токами:
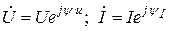 , (3.2)
, (3.2)
где  – амплитуды напряжения и тока;
– амплитуды напряжения и тока;
U, I – действующие значения напряжения и тока;
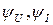 – начальные фазы напряжения и тока.
– начальные фазы напряжения и тока.
В символическом методе комплексные сопротивления элементов R, L, С равны соответственно
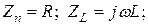
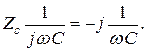 (3.3)
(3.3)
Комплексное сопротивление Z линейного пассивного двухполюсника (рис.3.1,а) в общем случае содержит активную и реактивную составляющие:
 (3.4)
(3.4)
где 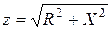 – полное сопротивление (модуль Z);
– полное сопротивление (модуль Z);
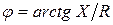 – угол сдвига фаз между напряжением и током двухполюсника (аргумент Z).
– угол сдвига фаз между напряжением и током двухполюсника (аргумент Z).
Комплексная проводимость Y пассивного двухполюсника, обратная комплексному сопротивлению Z:
 (3.5)
(3.5)
где  – полная проводимость (модуль Y);
– полная проводимость (модуль Y);
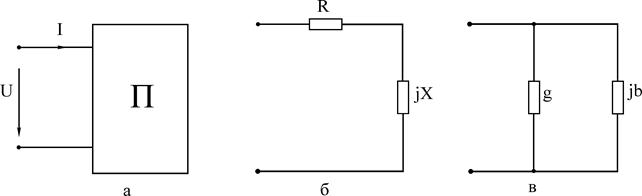
Рис.3.1
g – активная проводимость;
b – реактивная проводимость.
Выражению (3.4) соответствует последовательная схема замещения двухполюсника (рис. 3.1,б), а выражению (3.5) – параллельная (рис. 3.1,в). Переход от последовательной схемы замещения к параллельной осуществляют по формулам
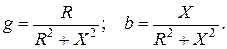 (3.6)
(3.6)
Для обратного перехода используют выражения
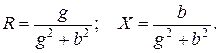 (3.7)
(3.7)
 |  | ||
Для расчетов токов и напряжений в цепях с единственным источником энергии применяют метод эквивалентных преобразований (МЭП). Например, для цепи на рис.3.2 две параллельные ветви с комплексными сопротивлениями
 заменяют одной эквивалентной ветвью с сопротивлением
заменяют одной эквивалентной ветвью с сопротивлением
Рис.3.2 Рис.3.3
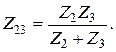
Тогда входное комплексное сопротивление цепи равно

Вычислив входной ток

токи 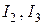 целесообразно рассчитать, используя «правило плеч»;
целесообразно рассчитать, используя «правило плеч»;
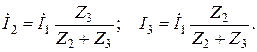 (3.8)
(3.8)
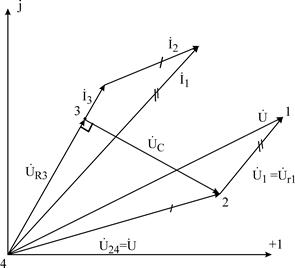
Расчет токов и напряжений завершается построением топографической диаграммы (рис.3.3). Построение диаграммы следует производить, взяв в качестве исходной точки «отрицательный» зажим источника, т.е. узел 4. Двигаясь против токов ветвей, строят на диаграмме векторы комплексных напряжений всех элементов цепи. Координаты точек 3, 2, 1 равны значениям комплексных потенциалов соответствующих узлов цепи (предполагается  ). Особенность диаграммы: вектор напряжения
). Особенность диаграммы: вектор напряжения 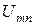 между любой парой узлов m и n направлен на диаграмме от узла n к узлу m. Для расчета цепи на рис.3.2, а также более сложных цепей лестничной структуры применяется метод пропорционального пересчета (МПП). В этом методе используется свойство линейной зависимости всех токов и напряжений цепи от амплитуды напряжения (тока) источника (в цепи единственный источник). Поясним суть метода для цепи на рис.3.2. Задается условно значение тока в наиболее удаленной и сложной ветви цепи. Пусть, например,
между любой парой узлов m и n направлен на диаграмме от узла n к узлу m. Для расчета цепи на рис.3.2, а также более сложных цепей лестничной структуры применяется метод пропорционального пересчета (МПП). В этом методе используется свойство линейной зависимости всех токов и напряжений цепи от амплитуды напряжения (тока) источника (в цепи единственный источник). Поясним суть метода для цепи на рис.3.2. Задается условно значение тока в наиболее удаленной и сложной ветви цепи. Пусть, например, 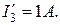 . Затем, находя условное напряжение
. Затем, находя условное напряжение  и условный ток
и условный ток  сложив токи
сложив токи 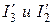 , находят ток
, находят ток  .
.
Тогда

Разделив истинное напряжение 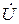 на условное
на условное 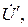 вычисляют комплексный коэффициент пересчета К:
вычисляют комплексный коэффициент пересчета К:

Для получения истинных напряжений и токов цепи необходимо все найденные ранее условные напряжения и токи умножить на коэффициент К, т.е.
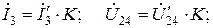
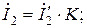


Для ориентировочных расчетов напряжений и токов применяется также графоаналитический метод расчета. Этот метод методологически связан с методом пропорционального пересчета, однако не использует алгебры комплексных чисел. Пусть, как и в предыдущем методе,  Выбрав масштабы
Выбрав масштабы  и
и  для напряжений и токов, откладывают в произвольном направлении ток
для напряжений и токов, откладывают в произвольном направлении ток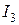 (например горизонтально). Затем строят вектор напряжения
(например горизонтально). Затем строят вектор напряжения 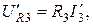 совпадающий по направлению с током
совпадающий по направлению с током 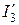 ,и вектор напряжения
,и вектор напряжения  отстающий по фазе от
отстающий по фазе от 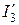 на 90°. Используя графические измерения, вычисляют напряжение
на 90°. Используя графические измерения, вычисляют напряжение  Вычислив
Вычислив 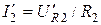 и откладывая ток
и откладывая ток 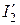 параллельно
параллельно 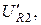 графически определяют
графически определяют 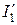 и т.д. В результате находят вектор условного напряжения U. Затем с помощью коэффициента пересчета K=U/U' вычисляют истинные токи и напряжения. Графические построения по ходу расчета дают в итоге условную топографическую диаграмму. Для получения истинной диаграммы следует, во-первых, увеличить линейные размеры всех векторов в К раз, во-вторых, повернуть против часовой стрелки условную диаграмму на угол
и т.д. В результате находят вектор условного напряжения U. Затем с помощью коэффициента пересчета K=U/U' вычисляют истинные токи и напряжения. Графические построения по ходу расчета дают в итоге условную топографическую диаграмму. Для получения истинной диаграммы следует, во-первых, увеличить линейные размеры всех векторов в К раз, во-вторых, повернуть против часовой стрелки условную диаграмму на угол  , равный разности начальных фаз векторов
, равный разности начальных фаз векторов  и.
и.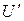 Активная и реактивная мощности потребителей вычисляются по формулам
Активная и реактивная мощности потребителей вычисляются по формулам
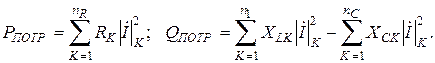
Комплексная мощность источника находится из

где 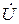 – комплексное напряжение источника;
– комплексное напряжение источника;
 – сопряженный комплексный ток источника.
– сопряженный комплексный ток источника.
Из закона сохранения энергии вытекают условия баланса активных и реактивных мощностей:
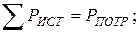
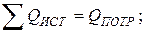
Описание лабораторной установки
В состав лабораторной установки входят перестраиваемый генератор синусоидального напряжения, вольтметр, фазометр и лабораторный макет. На макете смонтированы три резистора  конденсатор и катушка индуктивности. Для подключения генератора на макете имеется дополнительная пара зажимов.
конденсатор и катушка индуктивности. Для подключения генератора на макете имеется дополнительная пара зажимов.
Генератор. При установке частоты генератора следует ручку множителя частоты переключить в нужное положение и, вращая лимб генератора, установить требуемую частоту. Напряжение генератора устанавливается вращением ручки «Регулировка выхода».

 Измерение напряжения генератора производится только внешним вольтметром, вольтметр, встроенный в генератор, в лабораторных работах не используется.
Измерение напряжения генератора производится только внешним вольтметром, вольтметр, встроенный в генератор, в лабораторных работах не используется.
Вольтметр. В общем случае перед включением вольтметра переключатель пределов следует установить на предел 30 В и при небольших отклонениях стрелки прибора переходить на более низкие пределы. Цена деления вольтметра зависит от положения переключателя пределов и определяется как частное от деления установленного предела на число делений шкалы.
Фазометр. В работе возможно использование фазометра Ф2-1 со стрелочной индикацией или фазометра Ф2-34 с цифровой индикацией. Фазометр позволяет измерить угол сдвига фаз 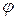 между двумя напряжениями одинаковой частоты, называемыми «Сигнал» и «Опорное», причем показание фазометра равно углу фазового сдвига напряжения «Сигнал» по отношению к опорному напряжению, т.е.
между двумя напряжениями одинаковой частоты, называемыми «Сигнал» и «Опорное», причем показание фазометра равно углу фазового сдвига напряжения «Сигнал» по отношению к опорному напряжению, т.е.
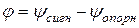 .
.
Фазометром можно измерить непосредственно угол сдвига фаз напряжений ветвей (элементов), имеющих общий узел. К общему узлу подключается зажим «Земля» фазометра. К двум оставшимся узлам подключаются клеммы «Опорное» и «Сигнал» фазометра, причем не принципиально, какое из напряжений принять в качестве опорного. Однако нужно следить, чтобы напряжения «Опорное» и «Сигнал» были направлены к общему узлу (напряжения 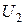 и
и  на рис.3.4,а).
на рис.3.4,а).
Из рис.3.4,б следует, что переход от напряжений 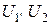 к обратным им напряжениям
к обратным им напряжениям 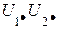 не изменяет фазового угла
не изменяет фазового угла 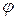 между ними как по величине, так и по знаку. Из сказанного ясно, что в качестве напряжений «Сигнал» и «Опорное» можно принять не только напряжения
между ними как по величине, так и по знаку. Из сказанного ясно, что в качестве напряжений «Сигнал» и «Опорное» можно принять не только напряжения 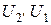 , направленные к зажиму «Земля», но в равной мере и обратные им напряжения
, направленные к зажиму «Земля», но в равной мере и обратные им напряжения  направленные от зажима «Земля». Назовем напряжения «Сигнал» и «Опорное» согласованными (по отношению к зажиму «Земля»), если они оба направлены к зажиму «Земля» или оба от зажима «Земля». Таким образом, показание фазометра на рис.3.4,а равно углу
направленные от зажима «Земля». Назовем напряжения «Сигнал» и «Опорное» согласованными (по отношению к зажиму «Земля»), если они оба направлены к зажиму «Земля» или оба от зажима «Земля». Таким образом, показание фазометра на рис.3.4,а равно углу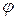 сдвига фаз между напряжением «Сигнал» и согласованным с ним напряжением «Опорное». Если же нас интересует угол а фазового сдвига между несогласованными напряжениями «Сигнал» и «Опорное», то из рис.3.4,б следует, что в этом случае к показанию фазометра
сдвига фаз между напряжением «Сигнал» и согласованным с ним напряжением «Опорное». Если же нас интересует угол а фазового сдвига между несогласованными напряжениями «Сигнал» и «Опорное», то из рис.3.4,б следует, что в этом случае к показанию фазометра 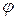 следует добавить или вычесть 180°, причем выбор знака для слагаемого 180° определяется только удобством представления угла а.
следует добавить или вычесть 180°, причем выбор знака для слагаемого 180° определяется только удобством представления угла а.

Рис. 3.4
Обобщая все сказанное выше, можно для рис.3.4,а записать
 (3.11)
(3.11)
 (3.12)
(3.12)
где 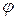 показание фазометра;
показание фазометра;
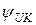 начальная фаза напряжения
начальная фаза напряжения 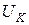 .
.
Если начальная фаза опорного напряжения равна нулю, то из (3.10) видно, что в этом случае фазометр регистрирует начальную фазу напряжения «Сигнал».
Фазометр может применяться для измерения начальных фаз токов ветвей, однако в этом случае напряжение «Сигнал» должно сниматься с резистивного элемента ветви, фаза напряжения в котором совпадает с фазой тока.
Фазометр Ф2-1 со стрелочной индикацией. Тумблер «Опережает, отстает» фазометра позволяет определить знак yгла j. Если отклонение стрелки прибора вправо достигается в положении тумблера «Опережает», тот 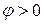 , если же в положении «Отстает», то
, если же в положении «Отстает», то 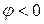 .
.
Фазометр работает устойчиво, если подводимые напряжения не менее 0,5 В.
Порядок работы Ф2–1
1. Установить переключатель пределов в положение «Калибр».
2. Установить тумблер в положение «Опережает».
3. Включить вилку шнура в сеть и затем включить тумблер «Сеть», прогреть прибор 5-10 минут.
4. Потенциометром «Калибр» установить стрелку прибора на деление 180° нижней шкалы.
5. Переключатель пределов перевести в положение «Уст.0» и ручкой потенциометра «Уст.0» установить стрелку прибора на деление 0.
6. Переключатель пределов переводится в один из рабочих пределов 180°, 100°, 50°, 25° только после подключения напряжений «Опорное» и «Сигнал».
7. Окончив измерения, вначале переключатель пределов перевести в положение «Калибр» и затем отключить напряжения.
Фазометр Ф2-34 с цифровой индикацией.
Порядок работы Ф2-34
1. Включить вилку шнура в сеть.
2. Переключателем «Сеть» включить прибор. При этом должна работать цифровая индикация прибора.
3. На разъем « )2» подать опорное напряжение.
)2» подать опорное напряжение.
4. На разъем « )1» подать напряжение сигнала.
)1» подать напряжение сигнала.
5. Нажать на кнопку «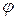 ». Ждать установки индикации примерно 1 мин. Об окончании установки свидетельствует периодическое свечение нижнего сегмента символьного разряда индикатора.
». Ждать установки индикации примерно 1 мин. Об окончании установки свидетельствует периодическое свечение нижнего сегмента символьного разряда индикатора.
В табл.3.1 заданы для шести вариантов параметры генератора  и номиналы элементов исследуемых схем. Величины
и номиналы элементов исследуемых схем. Величины 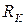 и
и 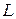 задают резистивное сопротивление и индуктивность для последовательной схемы замещения реальной катушки индуктивности. Конденсатор заменяется идеальной емкостью С.
задают резистивное сопротивление и индуктивность для последовательной схемы замещения реальной катушки индуктивности. Конденсатор заменяется идеальной емкостью С.
Домашнее задание
1. Для последовательной цепи на рис.З.5:
а) рассчитать согласно варианту сопротивления  реактивных элементов, комплексное входное сопротивление цепи, комплексный ток f и комплексные напряжения элементов
реактивных элементов, комплексное входное сопротивление цепи, комплексный ток f и комплексные напряжения элементов 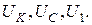 Параметры цепи и генератора заданы в табл.3.1 согласно варианту. Напряжение генераторе У=10 В. Начальную фазу напряжения генератора принять нулевой. Расчетные комплексные величины занести в табл.3.2 в графу «Расчет»;
Параметры цепи и генератора заданы в табл.3.1 согласно варианту. Напряжение генераторе У=10 В. Начальную фазу напряжения генератора принять нулевой. Расчетные комплексные величины занести в табл.3.2 в графу «Расчет»;
б) по результатам расчетов построить топографическую диаграмму напряжений всех элементов с указанием вектора тока.
2. Для параллельной цепи на рис.3.6 и указанных в  a параметров генератора:
a параметров генератора:
а) рассчитать по закону Ома комплексные токи 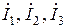 ветвей и входной ток
ветвей и входной ток  как их сумму. Результаты занести в табл.3.3 в графу «Расчет»;
как их сумму. Результаты занести в табл.3.3 в графу «Расчет»;
6) построить векторную диаграмму токов и напряжений.
3. В разветвленной цепи, заданной согласно варианту в табл.3.1:
а) рассчитать, используя метод эквивалентных преобразований, комплексные токи 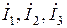 ветвей и комплексные напряжения всех элементов. Результат занести в табл.3.4 в графу «Расчет» (
ветвей и комплексные напряжения всех элементов. Результат занести в табл.3.4 в графу «Расчет» (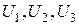 – напряжения на резисторах
– напряжения на резисторах  );
);
Таблица 3.1
| Вариант | Схема на рис. | 
| 
| 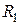
| 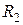
| 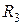
| 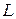
| 
| 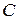 
|
| В | Гц | Ом | Ом | Ом | мГн | Ом | мкФ | ||
| 3.8 | 0.93 | ||||||||
| 3.8 | 0.93 | ||||||||
| 3.9 | 0.95 | ||||||||
| 3.9 | 42.5 | 0.99 | |||||||
| 3.10 | 0.96 | ||||||||
| 3.10 | 1.0 |
б) построить топографическую диаграмму напряжений всех элементов и совмещенную с ней векторную диаграмму токов. Для векторов напряжений и векторов токов желательно цветовое различие, масштабы для  и
и  взять достаточно крупными;
взять достаточно крупными;
в) составить и рассчитать уравнения баланса активных и реактивных мощностей цепи. Вычислить коэффициент мощности цепи.
Последовательность выполнения работы
Включить в сеть генератор, вольтметр, фазометр и дать им прогреться в течение 5 мин.
1. Собрать последовательную цепь на рис.3.5, соблюдая последовательность элементов и учитывая, что  — внутреннее активное сопротивление катушки индуктивности.
— внутреннее активное сопротивление катушки индуктивности.
Таблица 3.2
| Цепь на рис. 3.5 |

|

| 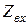
| 
| 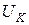
| 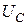
| 
| |||||||
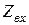
|
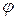
| I |

|
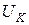
|
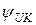
|
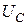
| 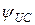
|

|
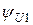
| |||||
| прям. | косв. | |||||||||||||
| Ом | Ом | Ом | град | мА | град | В | град | В | В | град | ||||
| Расчет | – | |||||||||||||
| Опыт |
Таблица 3.3
| Цепь на рис. 3.6 | I 
| 
| 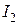
| 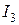
| ||||
| I | 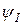
| 
| 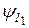
| 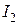
| 
| 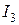
| 
| |
| мА | град | мА | град | мА | град | мА | град | |
| Расчет | ||||||||
| Опыт | – | – | – | – | – | – |
Таблица 3.4
| Разветвленная цепь | 
| 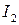
| 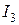
| U1 | U2 | U3 | 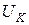
| 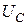
| |||||

| 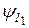
| 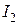
| 
| 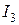
| 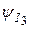
| 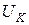
| 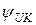
| 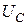
| 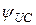
| ||||
| мА | град | мА | град | мА | град | В | В | В | В | град | В | град | |
| Расчет | |||||||||||||
| Опыт | – | – |
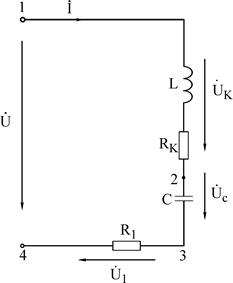 Рис.3.5
Рис.3.5
|
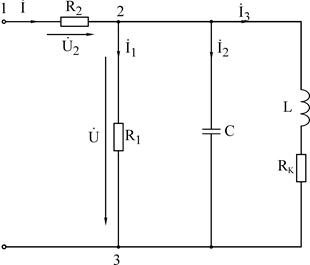 Рис.3.7
Рис.3.7
|
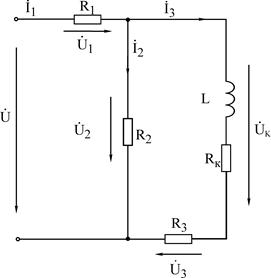 Рис.3.8
Рис.3.8
|
 Рис.3.9
Рис.3.9
|
 Рис.3.10
Рис.3.10
|
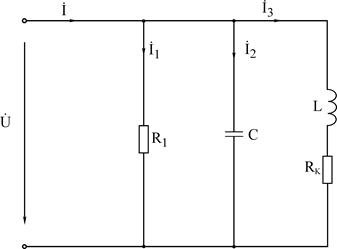 Рис.3.6
Рис.3.6
|
Подключить цепь к генератору, выставить частоту согласно варианту и установить с помощью настольного вольтметра (встроенный в генератор вольтметр в этой и последующих работах использовать нельзя) напряжение на входе цепи 10 В:
а) измерить вольтметром и занести в табл.3.2 в графу «Опыт» напряжения 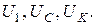 Пересчитать по закону Ома напряжения
Пересчитать по закону Ома напряжения  ;
;
б) измерить фазометром начальную фазу у тока I. (В качестве «Опорного» взять входное напряжение U, а в качестве «Сигнала» взять напряжение 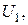 т.е. клемму «Земля» подключить к общему узлу 4, клемму «Сигнал» - к узлу 3, а клемму «Опорное» - к узлу 1. Обратить внимание, что напряжения
т.е. клемму «Земля» подключить к общему узлу 4, клемму «Сигнал» - к узлу 3, а клемму «Опорное» - к узлу 1. Обратить внимание, что напряжения  и
и 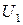 согласованы;
согласованы;
в) прямое измерение начальной фазы 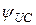 напряжения
напряжения 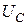 в цепи на рис. 3.5 невозможно, так как
в цепи на рис. 3.5 невозможно, так как 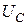 и
и  не имеют общего узла. Прямое измерение станет возможным, если на время измерения фазы поменять местами резистор
не имеют общего узла. Прямое измерение станет возможным, если на время измерения фазы поменять местами резистор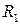 и С. Тогда фазометр подключается к тем же узлам, что и в пункте “б”. Выполнить это измерение. Результат занести в графу
и С. Тогда фазометр подключается к тем же узлам, что и в пункте “б”. Выполнить это измерение. Результат занести в графу 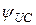 - прям.;
- прям.;
г) в реальных цепях перемена элементов местами не всегда возможна. По этой причине выполнить измерение начальной фазы 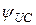 косвенным методом (без перемены местами R и С). Для этой цели зажим «Земля» фазометра подключить к узлу 3, зажим «Сигнал» - к узлу 2, а зажим «Опорное» - к узлу 4. Записать показания
косвенным методом (без перемены местами R и С). Для этой цели зажим «Земля» фазометра подключить к узлу 3, зажим «Сигнал» - к узлу 2, а зажим «Опорное» - к узлу 4. Записать показания 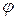 фазометра. Поскольку
фазометра. Поскольку 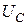 и
и  не согласованы, то угол
не согласованы, то угол  между
между  определим согласно (3.12), вычитая из показания
определим согласно (3.12), вычитая из показания 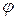 угол 180°. Если к результату прибавить измеренную раннее начальную фазу
угол 180°. Если к результату прибавить измеренную раннее начальную фазу  тока (совпадающую с начальной фазой для
тока (совпадающую с начальной фазой для 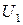 ), то получим начальную фазу для
), то получим начальную фазу для 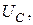 т.е.
т.е. 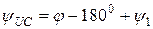 . Результат занести в графу
. Результат занести в графу 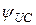 – косв. Сопоставить результаты прямого и косвенного измерений
– косв. Сопоставить результаты прямого и косвенного измерений  ;
;
д) начальная фаза 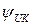 для
для  измеряется непосредственно (зажим «Земля» подключить к узлу 1, зажим «Сигнал» - к узлу 2, зажим «Опорное» - к узлу 4). Напряжения
измеряется непосредственно (зажим «Земля» подключить к узлу 1, зажим «Сигнал» - к узлу 2, зажим «Опорное» - к узлу 4). Напряжения  и
и  согласованы;
согласованы;
е) начальные фазы, измеренные в пп. б, в, г, занести в табл. 3.2 в графу «Опыт».
2. Собрать параллельную цепь на рис. 3.9 с добавочным резистором 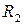 и выставить с помощью вольтметра напряжение U=10 B не на входе цепи, а на сопротивлении
и выставить с помощью вольтметра напряжение U=10 B не на входе цепи, а на сопротивлении 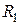 . В этом случае комплексные токи параллельных ветвей на рис.3.7 и 3.6 будут одинаковы. Наличие резистора
. В этом случае комплексные токи параллельных ветвей на рис.3.7 и 3.6 будут одинаковы. Наличие резистора  позволяет измерить входной ток
позволяет измерить входной ток  ;
;
а) измерить напряжение на 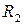 и пересчитать в ток
и пересчитать в ток  ;
;
б) при измерении фазы  , входного тока в качестве опорного следует взять напряжение
, входного тока в качестве опорного следует взять напряжение  на резисторе
на резисторе 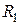 . Тогда клемму «Земля» нужно подключить к общему узлу 2, клемму «Сигнал» – к узлу 1, клемму «Опорное» – к узлу 3.
. Тогда клемму «Земля» нужно подключить к общему узлу 2, клемму «Сигнал» – к узлу 1, клемму «Опорное» – к узлу 3.
Внимание! Напряжения  2 и U не согласованы. Измеренный комплексный ток
2 и U не согласованы. Измеренный комплексный ток  занести в табл.3.3. Токи параллельных ветвей не измеряются.
занести в табл.3.3. Токи параллельных ветвей не измеряются.
3. Собрать разветвленную цепь согласно варианту (рис.3.10 – 3.12). Подключить к цепи генератор заданной частоты с напряжением U=10 В:
а) измерить вольтметром напряжения на резисторах 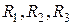 и напряжения
и напряжения 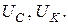 Пересчитать напряжения резисторов в токи
Пересчитать напряжения резисторов в токи 
б) измерить фазометром начальные фазы токов 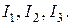 Занести в табл.3.4 в графу «Опыт» комплексные токи
Занести в табл.3.4 в графу «Опыт» комплексные токи 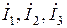 и модули напряжений
и модули напряжений 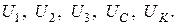
4.Сделать заключение о соответствии расчетных и опытных данных по всем выполненным пунктам работы.
Основные вопросы к работе
1.Основные величины, характеризующие синусоидальный ток и напряжение (период, частота, угловая частота, начальная фаза, амплитуда, действующее значение).
2.С какой целью введено понятие действующего значения гармонического сигнала? Может быть, достаточно понятия амплитуды сигнала?
3.Какой смысл содержится в понятии положительного направления синусоидального напряжения и тока?
4.Что такое комплексный ток, напряжение? Что понимают под комплексной амплитудой тока, напряжения?
5.Как вычисляются комплексные сопротивления элементов цепи?
6.Каковы фазовые сдвиги между напряжениеми током в индуктивности, емкости?
7.Для какого класса цепей (R-цепи, RL-цепи, RC-цепи, LC-цепи, RLC-цепи) угол 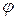 сдвига фаз между входными напряжением и током может равняться: а) нулю, б) ±90°?
сдвига фаз между входными напряжением и током может равняться: а) нулю, б) ±90°?
8. Что характеризуют активная, реактивная и полная мощности? Единицы их измерения.
9.Что такое коэффициент мощности?
10.На каком важном свойстве линейных цепей основан метод пропорционального пересчета?
11.Как строится топографическая диаграмманапряжений цепи?В чем ееотличие от векторной диаграммы напряжений?
12. Опишите особенности использования фазометра.
Лабораторная работа №3Б
ИССЛЕДОВАНИЕ РАЗВЕТВЛЕННОЙ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Цель работы
Определение параметров простейших эквивалентных схем замещения двухполюсника. Экспериментальная проверка законов распределения тока и напряжения в линейной разветвленной цепи гармонического тока, проверка балансов активных и реактивных мощностей, приобретение навыков работы с вольтметром, фазометром и генератором.
Основные теоретические положения
Лабораторная работа №3Б является углубленным вариантом предыдущей работы №3А. Поскольку ниже изложены только дополнительные теоретические сведения, следует предварительно ознакомиться с теоретическим материалом к работе №3А.
Рассмотрим схему включения фазометра и расчетные формулы для экспериментального определения параметров схемы замещения таких реальных элементов, как катушка индуктивности и конденсатор (рис. 3.13).

Рис.3.13
1. Катушка индуктивности. Если катушку индуктивности представить последовательной схемой замещения, то цепь на рис.3.14, а и соответствующая ей векторная диаграмма напряжений примут вид, приведенный на рис. 3.14, б.
Обратим внимание, что напряжение сигнала 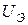 и опорное напряжение
и опорное напряжение  на рис.3.14,а не согласованы, поэтому угол а сдвиги фаз между ними (рис.3.14, б) вычисляется согласно формуле (3.12) в работе №3А путем добавления к показанию
на рис.3.14,а не согласованы, поэтому угол а сдвиги фаз между ними (рис.3.14, б) вычисляется согласно формуле (3.12) в работе №3А путем добавления к показанию 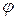 фазометра угла ±180°.
фазометра угла ±180°.
Из рис. 3.14, б находим
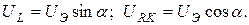

Рис.3.14
Учитывая, что
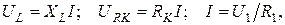
для параметров последовательной схемы замещения катушки получим
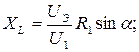
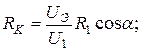 (3.13)
(3.13)
Для параллельной схемы замещения индуктивной катушки цепь на рис. 3.13 и векторная диаграмма примут вид, показанный на рис. 3.15.

Рис.3.15
Из рис. 3.15, а следует:

Поскольку из диаграммы на рис. 3.15, б видно, что

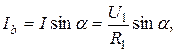
то для проводимостей параллельной схемы замещения катушки получим формулы
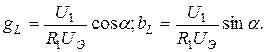 (3.14)
(3.14)
Формулы (3.14) можно получить и без анализа векторной диаграммы, если подставить выражения (3.13) в переходные формулы (3.6) из работы №ЗА.
2. Конденсатор. Методика вывода формул для параметров схем замещения конденсатора такая же, как и для катушки. Поэтому приведем только окончательные формулы.
 Рис.3.16
Рис.3.16
|
Для последовательной схемы замещения рис.3.16, а
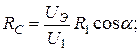 (3.15)
(3.15)
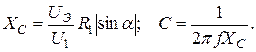 (3.16)
(3.16)
Для параллельной схемы замещения рис.3.16, б
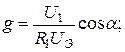 (3.17)
(3.17)
 (3.18)
(3.18)
В радиотехнике и электросвязи качество реальных катушек и конденсаторов оценивают с помощью их добротности Q на заданной частоте, которая характеризует степень приближения катушки к идеальной индуктивности и конденсатора – к идеальной емкости.
Добротность катушки
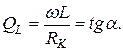 (3.19)
(3.19)
Добротность конденсатора
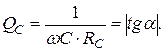 (3.20)
(3.20)
В формулах (3.19), (3.20) α – угол фазового сдвига между напряжением и током катушки и конденсатора (см. рис. 3.14,б). На практике добротность элементов измеряют с помощью специальных измерительных приборов – Q - метров, а формулы (3,19), (3,20) используют для расчета сопротивления потерь 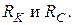 Отметим, что при использовании реальных элементов на фиксированной частоте в равной мере могут применяться как последовательная, так и параллельная схемы замещения катушки и конденсатора. Если же эксплуатация элементов осуществляется в некотором диапазоне частот, то для катушки предпочтительнее последовательная схема замещения, а для конденсатора - параллельная. Отмеченный приоритет схем замещения обусловлен тем, что параметры этих схем слабее зависят от частоты.
Отметим, что при использовании реальных элементов на фиксированной частоте в равной мере могут применяться как последовательная, так и параллельная схемы замещения катушки и конденсатора. Если же эксплуатация элементов осуществляется в некотором диапазоне частот, то для катушки предпочтительнее последовательная схема замещения, а для конденсатора - параллельная. Отмеченный приоритет схем замещения обусловлен тем, что параметры этих схем слабее зависят от частоты.
Описание лабораторной установки
Используемые в настоящей работе приборы (перестраиваемый генератор синусоидального напряжения, вольтметр, фазометр) и лабораторный макет такие же, как и в лабораторной работе №3А. Поэтому следует внимательно ознакомиться с описанием установки в работе №3А.
Особое внимание обратить на особенности использования фазометра. В табл. 3.5 заданы для шести вариантов параметры генератора  и номиналы элементов. Величины
и номиналы элементов. Величины 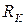 и
и 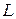 являются резистивным сопротивлением и индуктивностью последовательной схемы замещения катушки. При расчете домашнего задания конденсатор замещается идеальной емкостью С.
являются резистивным сопротивлением и индуктивностью последовательной схемы замещения катушки. При расчете домашнего задания конденсатор замещается идеальной емкостью С.
Таблица 3.5
| Вариант | Схема на рис. |  ,
В ,
В
|  ,
Гн ,
Гн
| 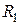 ,
Ом ,
Ом
| 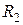 ,
Ом ,
Ом
| 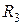 ,
Ом ,
Ом
| 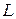 ,
мГн ,
мГн
|  ,
Ом ,
Ом
| 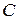 ,
мкФ ,
мкФ
|
| 3.17 | 0.93 | ||||||||
| 3.17 | 0.93 | ||||||||
| 3.18 | 0.95 | ||||||||
| 3.18 | 42.5 | 0.99 | |||||||
| 3.19 | 0.96 | ||||||||
| 3.19 | 1.0 |
Домашнее задание
Домашнее задание выполняется каждым студентом и включает следующие пункты:
1. Для последовательной цепи на рис. 3.5 (работа №3А):
а) рассчитать согласно варианту сопротивления  реактивных элементов комплексное входное сопротивление цепи, комплексный ток
реактивных элементов комплексное входное сопротивление цепи, комплексный ток  и комплексные напряжения элементов
и комплексные напряжения элементов 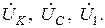 Параметры цепи и генератора заданы в табл.3.5. Потерями в конденсаторе пренебречь. Начальную фазу напряжения генератора принять равной нулю. Все расчетные величины занести в графу «расчет» табл. 3.6;
Параметры цепи и генератора заданы в табл.3.5. Потерями в конденсаторе пренебречь. Начальную фазу напряжения генератора принять равной нулю. Все расчетные величины занести в графу «расчет» табл. 3.6;
б) по результатам расчетов построить топографическую диаграмму напряжений всех элементов цепи.
Таблица 3.6
| Цепь на рис. 3.5 | 
| 
| 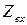
| 
| 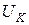
| 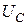
| 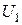
| ||||||

| 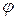
| 
| 
| 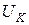
| 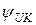
| 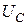
| 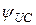
| 
| 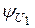
| ||||
| прям. | косв. | ||||||||||||
| Ом | Ом | Ом | град | мА | град | В | град | В | град | град | В | град | |
| Расч. | |||||||||||||
| Опыт | — | — |
2. Рассчитать на заданной частоте добротность 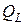 катушки (3.19) и проводимости
катушки (3.19) и проводимости 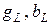 параллельной схемы замещения катушки (работа №3А, формула 3.6). Результаты занести в табл. 3.7.
параллельной схемы замещения катушки (работа №3А, формула 3.6). Результаты занести в табл. 3.7.
3. Для заданной в табл. 3.5 цепи (рис.3.17 - 3.19) рассчитать двумя методами (первый студент бригады — методом эквивалентных преобразований, второй студент бригады – методом пропорционального пересчета) комплексные токи  всех ветвей цепи, а также комплексные напряжения
всех ветвей цепи, а также комплексные напряжения 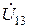 последовательной и
последовательной и  параллельных ветвей цепи (начальную фазу питающего напряжения принять равной нулю).
параллельных ветвей цепи (начальную фазу питающего напряжения принять равной нулю).
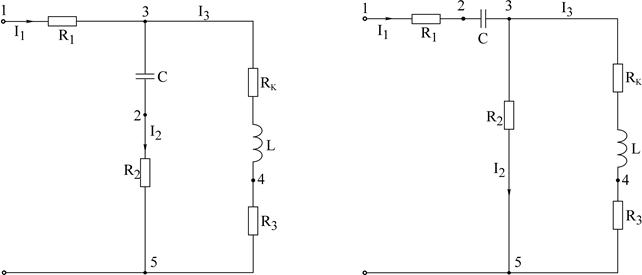
Рис.3.17 Рис.3.18
4. По расчетным данным п. 3 построить в единой системе координат векторную диаграмму токов и топографическую диаграмму напряжений. Масштабы 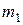 и
и  взять достаточно крупными и разными.
взять достаточно крупными и разными.

Рис.3.19 Рис.3.20
Таблица 3.7
| Расчет | ||||||||||||||
| 
| 
| 
| 
| 
| 
| 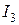
| 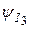
| 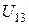
| 
| 
| 
| 
| 
|
| См | См | мА | град | мА | град | мА | град | В | град | В | град | Вт | вар | |
Таблица 3.8
| Опыт | |||||||||||||||
| Катушка индуктивности | Конденсатор | ||||||||||||||
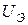
| 
| 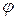
| 
| 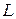
| 
| 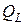
| 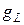
| 
| 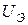
| 
| 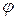
| 
| 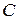
| 
| 
|
| В | В | град | град | мГн | Ом | См | См | В | В | град | град | мкФ | Ом | ||
Таблица 3.9
| Опыт | |||||||||||||||
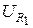
| 
| 
| 
| 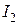
| 
| 
| 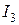
| 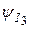
| 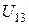
| 
| 
| 
| 
| 
| |
| В | мА | град | В | мА | град | В | мА | град | В | град | В | град | Вт | вар | |
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов