Интегральный метод

Интегральный метод, или метод Берглунда, основан на анализе равновесной низкочастотной вольт-фарадной характеристики. Поскольку для равновесной низкочастотной C‑V кривой справедливо (3.98), то

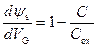. (3.116)

Интегрируя соотношение (3.116) с граничными условиями ψ_s = ψ_si, V_G = V_Gi, получаем:

. (3.117)

Поскольку C(V_G) – это экспериментальная кривая, то интегрирование уравнения (3.117) (потому метод и назван интегральным) сразу дает связь между поверхностным потенциалом и напряжением на затворе V_G. Выбор значений ψ_s1 и V_G1 произволен. Обычно величину ψ_s1 выбирают равной нулю (ψ_s1 = 0) и соответственно V_G1 – это напряжение плоских зон V_FB. Эти значения берутся из высокочастотных C‑V кривых. Так как известна связь V_G(ψ_s), то из равенства (3.99) после нескольких преобразований следует:

. (3.118)

Соотношение (3.118) позволяет определить величину и закон изменения плотности поверхностных состояний по всей ширине запрещенной зоны, что является преимуществом интегрального метода по сравнению с дифференциальным.

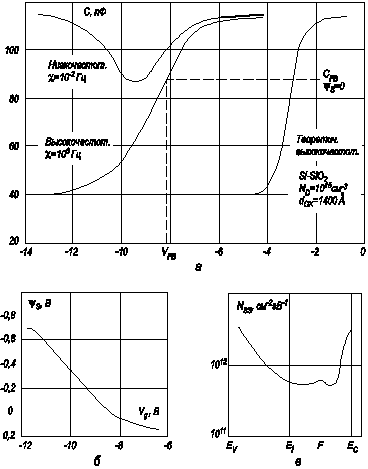
Рис. 3.20. Расчет плотности поверхностных состояний интегральным методом:

а) экспериментальная равновесная ВФХ МДП‑системы Si‑SiO₂‑Al; б) зависимость поверхностного потенциала ψ_s от напряжения V_G, рассчитанная из этой кривой по уравнению (3.117); в) зависимость плотности ПС от энергии E в запрещенной зоне полупроводника, рассчитанная из уравнения (3.117) по этим экспериментальным данным

Из соотношения (3.117) следует, что численное интегрирование функции (1 - С/С_ox) должно дать величину площади над равновесной C‑V кривой. Поскольку емкость выходит на насыщение C → C_ox при примерно одинаковых значениях поверхностного потенциала, то следует ожидать, что у кривых с разной плотностью поверхностных состояний площадь под кривой C‑V будет одинакова. На рисунке 3.20а, б, в приведены этапы расчета равновесных C‑V кривых и даны соответствующие графики.