Воздействие гармонических колебаний на RLC-цепь
Термин гармоническое воздействие применяется в случаях, когда мгновенное значение э.д.с. или тока задающего независимого источника изменяется по закону

где Um - амплитуда воздействия, ω - круговая частота, ψ - начальная фаза.
С целью упрощения дальнейших выкладок примем, что гармоническое воздействие имеет нулевую начальную фазу (ψ = 0).
При воздействии гармонического колебания на цепь RLC дифференциальное уравнение для напряжений в контуре будет выглядеть следующим образом:
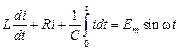 . (6.25)
. (6.25)
От ранее полученного выражения (6.15) оно отличается только правой частью.
Общее решение неоднородного уравнения (6.25) для напряжения на емкости будем искать в виде
 . (6.26)
. (6.26)
Ранее было показано, что в реальных цепях свободная составляющая со временем убывает по экспоненциальному закону (действительные и сопряженные комплексные корни находятся в левой части комплексной плоскости).
Следовательно, спустя некоторое время после приложения гармонического воздействия к цепи (точнее после завершения переходного процесса) в ней устанавливается режим гармонических колебаний. Другими словами, будет иметь значение лишь частное решение неоднородного дифференциального уравнения при t→∞.
Гармонические колебания тока в этой цепи описываются частным решением неоднородного уравнения (6.15), которое будем искать в виде
 . (6.27)
. (6.27)
Подставим это значение тока в уравнение (6.25) и после выполнения операций дифференцирования и интегрирования получим
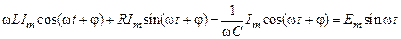 , (6.28)
, (6.28)
или
 , (6.29)
, (6.29)
Уравнение (6.29) справедливо для любых значений t. В частности для ωt=0
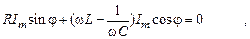
а для ωt = π/2
 .
.
Из первого уравнения получим
 , (6.30)
, (6.30)
После суммирования квадратов обоих уравнений


 . (6.31)
. (6.31)
Уравнения (6.30) и (6.31) определяют соответственно фазу и амплитуду гармонического тока (6.27) в цепи RLC в установившемся режиме.
Установившееся напряжение на емкости после подключения синусоидального напряжения ко входу будет определяться как
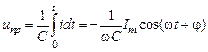 . (6.32)
. (6.32)
Обозначим через
 , (6.33)
, (6.33)
где Z - называют полное сопротивление.
Тогда для цепи, находящейся под воздействием гармонического тока, можно записать соотношение, аналогичное закону Ома
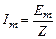 . (6.34)
. (6.34)
Разность
 (6.35)
(6.35)
принято называть реактивным сопротивлением.
С учетом введенного обозначения полное сопротивление
 (6.36)
(6.36)
и угол
 ,
, 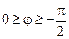 . (6.37)
. (6.37)
При Х > 0 говорят, что полное сопротивление Z носит индуктивный характер, при этом ток отстает по фазе от запитывающего напряжения на угол угол φ
При Х < 0 полное сопротивление Z носит емкостной характер и ток в цепи опережает по фазе входное напряжение на угол φ
 .
.
Общее решение (6.26) можно записать в виде суммы свободной и принужденной составляющих
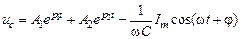
В момент времени t = 0 емкость С разряжена, а поскольку ток через индуктивность не может изменяться скачком, то в момент t=0 ток в цепи RLC также равен нулю
uС(0) = -0 , i(0) = 0.
В таком случае для этих начальных условий можно записать для напряжений

Так как ток в контуре равен
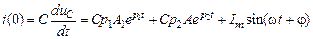 ,
,
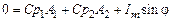 ,
,
то в соответствии с начальными условиями
 ,
,
 .
.
Для упрощения дальнейших рассуждений введем обозначения
 , (6.38)
, (6.38)
 . (6.39)
. (6.39)
Тогда совместное решение уравнений
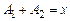 ,
,
 ,
,
даст следующие значения:
 и
и  .
.
Свободная составляющая колебаний для комплексных сопряженных корней 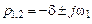 равна
равна

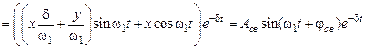 ,
,
где
 и
и 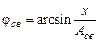 .
.
С учетом принужденной составляющей окончательно получим:
 . (6.40)
. (6.40)
Таким образом, согласно выражению (6.40) во время переходного процесса происходит суммирование затухающих колебаний с частотой ω1, зависящей только от параметров самого контура, и частотой ω, определяемой частотой приложенного напряжения.
В частном случае, при подключении синусоидального напряжения с частотой ω0 картина значительно упрощается. Действительно, при этих условиях
 ,
,
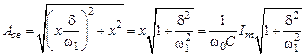 ,
,
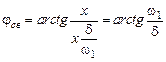 ,
,
 .
.
Добротностью последовательного контура, как известно, называется
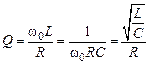 .
.
На практике типичные значения добротности контуров лежат в пределах от нескольких десятков до сотен, поэтому, когда Q>>1
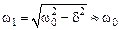 ,
, 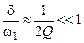 .
.
Выражение для напряжения на емкости контура RLC будет выглядеть следующим образом:
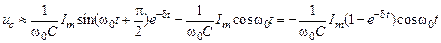 .
.
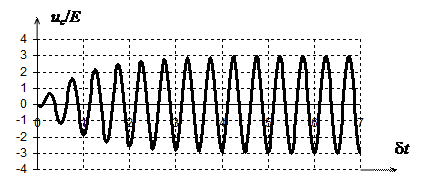 |
На рис. 6.9 представлен график напряжения, построенный в соответствии с последним выражением.
Рис.6.9. Напряжение на емкости последовательного колебательного контура при подаче на его вход синусоидального напряжения
Важно, что время установления колебаний тем больше, чем выше добротность контура.