МЕТОДИКА ИДЕНТИФИКАЦИИ
ИДЕНТИФИКАЦИЯ ПОРЯДКА РАЗНОСТИ
Ранее было показано, что автокорреляционная функция стационарного смешанного процесса авторегрессии – скользящего среднего удовлетворяет разностному уравнению 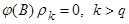 . Кроме того, если
. Кроме того, если 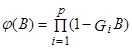 решение этого разностного уравнения для k-ой автокорреляции в предположении об отсутствии кратности корней имеет вид:
решение этого разностного уравнения для k-ой автокорреляции в предположении об отсутствии кратности корней имеет вид:
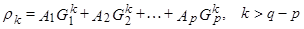 (8)
(8)
Условие стационарности, требующее, чтобы корни 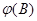 лежали вне единичного круга, приводит к тому, что корни
лежали вне единичного круга, приводит к тому, что корни 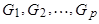 лежат внутри единичного круга.
лежат внутри единичного круга.
Из (8) следует, что для стационарной модели, у которой ни один из корней не лежит близко к границе единичного круга, автокорреляционная функция быстро затухает при средних и больших k.
Положим теперь, что один действительный корень, например, 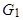 , приближается к 1, так что
, приближается к 1, так что 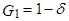 , где
, где 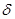 - малое положительное число. Тогда поскольку для больших k
- малое положительное число. Тогда поскольку для больших k 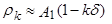 или
или 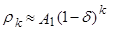 автокорреляционная функция не будет быстро затухать, а будет спадать медленно и почти линейно. Подобные рассуждения можно привести и в случае, когда к единице приближается не один корень.
автокорреляционная функция не будет быстро затухать, а будет спадать медленно и почти линейно. Подобные рассуждения можно привести и в случае, когда к единице приближается не один корень.
Следовательно, отсутствие у автокорреляционной функции тенденции к затуханию может рассматриваться как свидетельство того, что существует корень, близкий к 1. Выборочная автокорреляционная функция похожа на теоретическую. Отсюда (!) отсутствие затухания выборочной автокорреляционной функции логично истолковывать в том смысле, что процесс  ведет себя не стационарно, хотя возможно, его разность
ведет себя не стационарно, хотя возможно, его разность 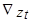 или какая-либо более высокая разность стационарна.
или какая-либо более высокая разность стационарна.
Итак, нестационарность подсказывается отсутствием быстрого спада выборочной автокорреляционной функции.
И тогда, предполагается, что необходимая для получения стационарности степень разности d достигнута, если автокорреляционная функция ряда 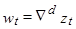 быстро затухает.
быстро затухает.
На практике d обычно равно 0, 1 или 2, и достаточно просмотреть примерно 20 первых значений автокорреляции исходного ряда, его первых и вторых разностей.