СВОБОДНАЯ КВАНТОВАЯ ЧАСТИЦА
Рассмотрим поведение свободной квантовой частицы в координатном представлении, где
 = -iiÑ,
= -iiÑ,  =
=  ,
,
а гамильтониан имеет вид
 = -i2/2mÑ2 ,
= -i2/2mÑ2 ,
(m - масса частицы). Гамильтониан не меняется при трансляциях (см. пример), а потому
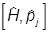 = 0,
= 0,
и импульс сохраняется. В полный набор можно включить  и
и  - всего четыре оператора. Но степеней свободы три. Дело просто в том, что не все четыре оператора независимы:
- всего четыре оператора. Но степеней свободы три. Дело просто в том, что не все четыре оператора независимы:  выражается через
выражается через  .
.
Возьмем в качестве операторов полного набора  . Они имеют общие собственные функции
. Они имеют общие собственные функции
fp(r) =  ei/i pr
ei/i pr
Каждая из них является собственной и для гамильтониана:
 fp(r)=- i2/2mÑ2
fp(r)=- i2/2mÑ2 ei/i pr=-
ei/i pr=-
 ei/ipr = p2/2m fp(r)
ei/ipr = p2/2m fp(r)
Таким образом, функции fp(r) описывают стационарные состояния частицы со значениями энергии
E = p2/2m.
Полная собственная функция гамильтониана, т.е. волновая функция стационарного состояния с зависимостью от времени, имеет вид
y(r,t) = e-i/i Ety(r).
В нашем случае
yp(r,t) =  e-i/i p2t/2m ×e i /i pr.
e-i/i p2t/2m ×e i /i pr.
Можно взять и другой полный набор:  и
и  (единичный вектор в направлении импульса). Так как
(единичный вектор в направлении импульса). Так как  = 1, то у него всего два независимых компонента. Добавляя гамильтониан, получим три оператора, как и должно быть. При таком выборе полного набора полные волновые функции стационарных состояний с учетом |p| =
= 1, то у него всего два независимых компонента. Добавляя гамильтониан, получим три оператора, как и должно быть. При таком выборе полного набора полные волновые функции стационарных состояний с учетом |p| = 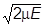 запишутся как
запишутся как
yE,n(r,t) = Ce-i/i Et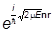 .
.
Константа C находится из условия нормировки, но в данном случае ее проще найти из условия полноты системы волновых функций.
Проведем эту достаточно утомительную выкладку. В абстрактном гильбертовом пространстве условие полноты записывается как
 |E,n.tñ áE,n.t|=
|E,n.tñ áE,n.t|=  .
.
Перейдем к координатному представлению, умножая это равенство слева на ár,а справа на|rRñ:
 òdE ár|En,tñ áEn,t|rRñ = ár |rRñ.
òdE ár|En,tñ áEn,t|rRñ = ár |rRñ.
Отсюда получаем:


 = d(r-rR).
= d(r-rR).
Находим и дифференциалы:
dp= p2dpdn, |n|= 1; p2/2m = E, dE=|p|dp/2m, dp=2m/p dE.
dp= p22m/p×dEdn= 2mpdEdn= 2m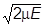 dEdn= (2 m 3/2 )E1/2dEdn;
dEdn= (2 m 3/2 )E1/2dEdn;
dEdn= dp/(2m)3/2 E1/2.
Переходим в интеграле к dp и к p в показателе экспоненты и вспоминаем условие нормировки обычных волн де Бройля:
òdp/(2m)3/2E1/2×|C|2e-ip(r-rR)/I = d(r-rR)= 1/(2pi)3òe-ip(r-rR)/idpÞ
C = 2m3E)1/4 /(2pi)3/2 .
Окончательно для нормированных волновых функций стационарных состояний имеем:
yE,n(r,t) = 