ЧАСТИЦА В БЕСКОНЕЧНОЙ ПРЯМОУГОЛЬНОЙ ЯМЕ
Рассмотрим поведение квантовой частицы в бесконечной прямоугольной потенциальной яме
|
V(x) = 
.
Стационарное уравнение Шредингера
-
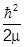yRR(x) + V(x)y(x)= E y(x)
имеет в качестве решения y(x) = 0 вне ямы. Поэтому нужно решать задачу на интервале
0 < x < l, где
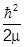-yRR(x) = Ey(x)
с граничными условиями
y(0) = 0, y(l) = 0.
Вводя обозначение
2mE/i2 = k2
запишем уравнение Шредингера как
yRR(x) + k2y(x) = 0.
Общее решение уравнения имеет вид
y (x) = Aeikx + Be-ikx.
Если E< 0, то k чисто мнимо, и обозначим его как ig. Тогда
y (x) = Ae -gx + Be gx.
Граничные условия дают
A + B = 0, Ae -gl + Be gl = 0,
откуда
Ash(gl) = 0.
Отсюда или A=0, и y=0, или g=0, и все равно y=0. Поэтому значения энергии могут быть только положительными.
Пусть это так. Тогда граничные условия дадут
A + B = 0, Ae ikl + Be -ikl = 0,
откуда
Asin(kl) = 0.
Так как A ¹ 0, то sin(kl) = 0, откуда kl = pn, где n = ±1, ±2, .... Для энергии
E = i2 k2 /2m = i2 /2m × (pn/l)2,
т.е. получаем дискретный энергетический спектр
En = p2i2/2ml2 × n2.
Волновые функции стационарных состояний теперь запишутся как
yn(x) = Asinknx,
причем вырождения нет, так как числам n и -n отвечают волновые функции, различающиеся только знаком, а значит описывающие одно состояние. Таким образом, спектр не только дискретный и простой. Константу A находим из условия нормировки:
1 = (yn ,yn) =
dx =
= |A|2l/2 Þ A = (2/l)1/2
и окончательно для нормированных волновых функций стационарных состояний имеем:
yn(x) = (2/l)1/2sinpn/l×x.
Для движения свободной частицы мы имели
fp(x) = 1/(2pi)1/2ei/i px.
Это есть обобщенная волновая функция. Так как квадрат ее модуля есть константа, то частицу с равной вероятностью можно найти в любой точке прямой. Это соответствует инфинитному движению частицы. В нашем случае получилась обычная волновая функция, равная нулю вне интервала (0,l). Это значит, что мы можем найти ее только внутри ямы, что соответствует финитному движению. В этом принципиальная разница между двумя рассмотренными случаями.