рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Электроника
- /
- УРАВНЕНИЕ КЛЕЙНА-ГОРДОНА
Реферат Курсовая Конспект
УРАВНЕНИЕ КЛЕЙНА-ГОРДОНА
УРАВНЕНИЕ КЛЕЙНА-ГОРДОНА - раздел Электроника, ОСНОВЫ КВАЗИРЕЛЯТИВИСТСКОЙ КВАНТОВОЙ ТЕОРИИ Делая В Этом Выражении Подстановки E ® I...
Делая в этом выражении подстановки
E ® i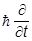 , p® -i
, p® -i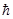 Ñ,
Ñ,
получим
-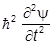 = (-c2
= (-c2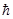 2Ñ2 + m2c4)y = 0
2Ñ2 + m2c4)y = 0
или
Ñ2y - 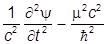 y = 0.
y = 0. 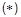
Вводя инвариантный оператор Даламбера
ð = 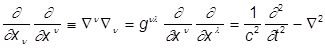 ,
,
запишем уравнение в явно ковариантной форме
ðy + (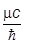 )2y = 0
)2y = 0 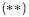
К нему можно прийти и из ковариантного соотношения
p2 = pnpn = m2c2,
делая в нем подстановки
pn ® -i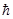
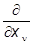 º -i
º -i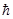 Ñn.
Ñn.
Так или иначе, имеем релятивистский аналог уравнения Шредингера, которое называется уравнение Клейна-Гордона.
Умножая 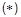 слева на y*, а сопряженное уравнение слева на y и производя вычитание, после элементарных выкладок получим уравнение непрерывности
слева на y*, а сопряженное уравнение слева на y и производя вычитание, после элементарных выкладок получим уравнение непрерывности
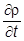 + divj= 0,
+ divj= 0,
выражающее некий закон сохранения, в котором

и
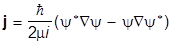 .
.
Можно поступить иначе: умножить 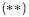 на y*, а сопряженное уравнение на y и вычесть. Тогда получим уравнение непрерывности в ковариантной форме
на y*, а сопряженное уравнение на y и вычесть. Тогда получим уравнение непрерывности в ковариантной форме
Ñmjm = 0,
где
jm = y*Ñmy - yÑmy*.
Расписывая по компонентам, получим те же результаты.
Вектор jполучился абсолютно таким же, как в нерелятивистской квантовой механике, а там мы его отождествили с вектором плотности потока вероятности. Но там плотность вероятности была
r = |y|2 º y*y,
а здесь для нее получилось другое выражение. Казалось бы, и здесь новое r можно интерпретировать как плотность вероятности. Но такая интерпретация не проходит. Уравнение Клейна-Гордона - второго порядка по времени, а потому для него необходимо задать 2 начальных условия - для y и 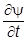 . И их всегда можно подобрать так, что будет r<0. Мало того, если при t=0 r>0, то по истечении времени может быть как r>0, так и r<0, т.е. плотность вероятности будет индефинитной, тогда как она должна быть всегда по самому смыслу быть положительно определенной.
. И их всегда можно подобрать так, что будет r<0. Мало того, если при t=0 r>0, то по истечении времени может быть как r>0, так и r<0, т.е. плотность вероятности будет индефинитной, тогда как она должна быть всегда по самому смыслу быть положительно определенной.
Видим, что трудность проистекает из-за того, что в уравнении - вторая производная по времени. Попытаемся получить релятивистское уравнение первого порядка по времени. Но в СТО время и координаты равноправны, поэтому уравнение должно быть первого порядка и по координатам. Общий вид такого уравнения
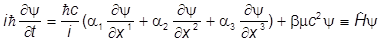 ,
,
где 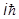 в самом начале поставлено просто для удобства, для сравнения с обычным уравнением. Здесь a1, a2, a3 и b - некоторые неизвестные коэффициенты. Ясно, что
в самом начале поставлено просто для удобства, для сравнения с обычным уравнением. Здесь a1, a2, a3 и b - некоторые неизвестные коэффициенты. Ясно, что 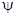 не может быть обычной скалярной функцией, ибо при обычном трехмерном вращении левая часть не изменится, а правая преобразуется как вектор. Поэтому считаем y многокомпонентной (с дополнительными внутренними степенями свободы):
не может быть обычной скалярной функцией, ибо при обычном трехмерном вращении левая часть не изменится, а правая преобразуется как вектор. Поэтому считаем y многокомпонентной (с дополнительными внутренними степенями свободы):
y = 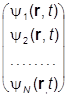 .
.
Поэтому на самом деле нужно писать не y, а ys(r,t), и отсюда уже почти ясно, что aj и b должны быть не обычными числами, а матрицами.
Каждый компонент ys должен подчиняться уравнению Клейна-Гордона
- 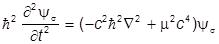 ,
,
так как оно выражает лишь релятивистское соотношение между pи Е. Это сейчас позволит нам найти коэффициенты aj, b. Для этого берем уравнение
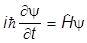
и действуем на обе его части оператором 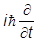 =
=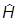 :
:
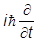 (
(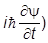 =
= 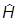 (
(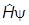 ).
).
Подставляя явное выражение 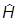 и производя аккуратно (с учетом возможной некоммутативности aj и b) перемножение, получим
и производя аккуратно (с учетом возможной некоммутативности aj и b) перемножение, получим
- 
(по двойным индексам - суммирование от 1 до 3). Чтобы это уравнение совпало с УКГ, необходимо потребовать
aiaj + ajaI = 2dij, aib + baI = 0, b2 =1. (***)
Отсюда уже абсолютно ясно, что aj, b - матрицы, а потому 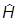 - матричный (и дифференциальный) оператор. Поскольку
- матричный (и дифференциальный) оператор. Поскольку 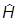 должен быть эрмитовым оператором, то aj, b-квадратные матрицы, причем порядка N´N, где N - число компонентов у ys. Система уравнений (***) неразрешима при слишком малых N(=1,2,3). Минимальное N, при котором система перестает быть переопределенной, есть N=4 (вообще можно доказать, что N должно быть четным, мало того, оно должно быть квадратом, так что следующее N есть N=16). Одно из возможных решений таково:
должен быть эрмитовым оператором, то aj, b-квадратные матрицы, причем порядка N´N, где N - число компонентов у ys. Система уравнений (***) неразрешима при слишком малых N(=1,2,3). Минимальное N, при котором система перестает быть переопределенной, есть N=4 (вообще можно доказать, что N должно быть четным, мало того, оно должно быть квадратом, так что следующее N есть N=16). Одно из возможных решений таково:
ai = 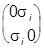 , b =
, b = 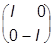 ,
,
где si - матрицы Паули:
s1=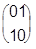 , s2=
, s2=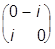 , s3=
, s3=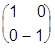 ; I=
; I=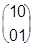 .
.
Существуют и другие решения, но они не дают новой физики, ибо связаны с предыдущим преобразованием унитарной эквивалентности.
Итак, получаем уравнение Дирака
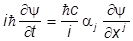 +bmc2y,
+bmc2y,
где матрицы Дирака подчиняются соотношениям (***), и один из наборов выписан явно выше. Функция y на самом деле есть 4-компонентный столбец
y(r,t) = 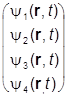 ,
,
и в более подробной форме записи уравнение Дирака выглядит так:
 +bmc2ys
+bmc2ys
На самом деле это система четырех уравнений для четырех функций ys.
Уравнение Дирака можно записать гораздо более симметрично, если умножить обе его части слева на b и ввести новые матрицы 4´4
g0 = b, gj = baj = g0aj,
удовлетворяющие антикоммутационным соотношениям
gm gn + gngm = 2gmn.
Тогда получим
ign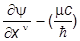 y = 0.
y = 0.
Именно в этой форме записи удобнее всего исследовать свойство релятивистской инвариантности.
Введем сопряженную функцию
y+ = (y1*,y2*,y3*,y4*),
которая подчиняется уравнению, сопряженному дираковскому:
-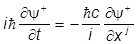 aj + bmc2y+.
aj + bmc2y+.
Умножая уравнение Дирака слева на y+, а сопряженное справа на y, найдем
i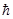 y+
y+ 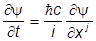 aj y+ + bmc2y+y.
aj y+ + bmc2y+y.
и
- i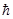 y
y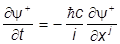 aj y + bmc2y+y
aj y + bmc2y+y
Производим вычитание
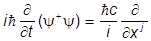 (y+aj y).
(y+aj y).
В итоге получаем уравнение непрерывности
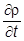 + divj= 0,
+ divj= 0,
где
r = y+y,j= cy+ay [a º (a1, a2, a3)].
Величина r положительно определена:
r = êy1ê2 + êy2ê2 + êy3ê2 + êy4ê2
и может быть интерпретирована как плотность вероятности, чего нельзя было сделать в случае уравнения Клейна-Гордона. Она очень похожа на обычную плотность вероятности, только содержит 4 слагаемых. Но вектор j, интерпретируемый как плотность потока вероятности, теперь существенно изменился; в частности, он не содержит пространственных координат.
Будем искать решение уравнения Дирака в виде
yEp(r,t) = w(E,p)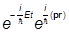 ; w º
; w º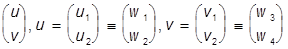 .
.
Подставляя все это в уравнение Дирака и учитывая явный вид матриц aj и b, получим алгебраическую систему формально двух, на самом деле четырех уравнений
Eu = c(sp)v + mc2u
Ev = c(sp)u - mc2v ,
где
s= {s1, s2, s3}, sp= s1p1 + s2p2 + s3p3 = sjpj.
Условие нетривиальной разрешимости дает
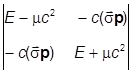 = 0
= 0
откуда
Е2 - m2c4 - c2(sp)2 = 0.
Раскрываем
(sp)2 = (sp)(sp) = sjpj skpk = (sjsk)(pjpk).
Учитывая, что
sjsk = 0 (j ¹k), (sj)2 = I,
получим
(sp)2 = p2,
и условие разрешимости запишется как
Е2 - m2c4 - c2p2 = 0.
Таким образом, нетривиальные решения существуют лишь при
Е = 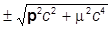 º ±ep,
º ±ep,
а это есть релятивистское соотношение между энергией и импульсом (но появились оба знака!).
Так как det=0, то второе уравнение будет следствием первого, и его можно не рассматривать, но лучше бывает оставить второе, а выкинуть первое. При Е=ep задает u произвольно, тогда из второго
v =  u.
u.
Но само u содержит две линейно независимые функции:
u(p) = u01(p) +u02(p) = 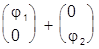 .
.
Поэтому находим при Е=ep>0:
w+l = 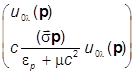 , (l = 1,2).
, (l = 1,2).
Вторую пару решений получим при Е = -ep < 0. Теперь будем считать заданным
v(p) = v01(p) = v02(p) = 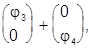
и из первого уравнения системы получим
u = - v.
v.
Поэтому находим при Е = -ep < 0:
w-l(p) = 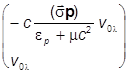 .
.
Таким образом, внутренними переменными, значения которых характеризуют разные решения, являются знак энергии (+ и -), а также величина l. Ее значения l=1, 2 нумеруют решения внутри верхней пары u и нижней пары v компонентов полной волновой функции.
– Конец работы –
Эта тема принадлежит разделу:
ОСНОВЫ КВАЗИРЕЛЯТИВИСТСКОЙ КВАНТОВОЙ ТЕОРИИ
ОСНОВЫ КВАЗИРЕЛЯТИВИСТСКОЙ КВАНТОВОЙ ТЕОРИИ... Продолжение УРАВНЕНИЕ...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: УРАВНЕНИЕ КЛЕЙНА-ГОРДОНА
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов