Цепи переменного тока. Импеданс.
а) перем ток в цепи с активн сопративл
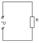 U=Umcoswt
U=Umcoswt
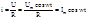
Колеб силы тока происх в такой же фазе, что и напр.
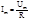
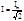
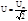
Действ знач силы перем тока наз сила такого пост. тока которое произв такое теплов действие как и при перем токе.
б) перем ток в цепи с емкостью
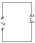 U=Umcoswt q=CU=CUmcos wt
U=Umcoswt q=CU=CUmcos wt
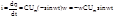
По ф-ле приведения: -sinwt=cos(wt+p/2)
i=wCUm cos(wt+p/2)
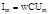
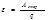
в) пер ток в цепи с индуктивностью
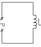
U=Umcoswt esi=-L*(di/dt) U= -esi Umcoswt=L(di/dt)
di=(Um/L)*coswt dt 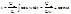
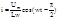
Амплитуда:
Im=Um/wL => XL=Um/Im=wL
г) перем ток в цепи с элементами R,C,L
 Сила перем тока изм на всех участках цепи одинак.
Сила перем тока изм на всех участках цепи одинак.
Импеданс:
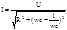
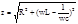
4. Гармонич. колеб.Диф. ур-е гарм. колеб. и его реш.
В колеб контуре сумма падений напряжения на индуктивности и на емкость равна нулю, поэтому 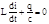 Введем обозн i=q
Введем обозн i=q 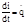 и перепишем
и перепишем 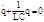
Поскольку L м С- величины сугубо положительные, можно ввести обозн 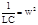 тогда
тогда 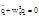
Таким образом, колеб заряда на обкладк конденсатора описыв-ся лин однородным дифференциальным ур-ем второго порядка. Необходимо найти такую связь между q и t , чтобы она удовлетворяла этому уравнению. Реш дифф уравнения является выражений вида q=qmcosj=qmcos(w0t+j0) , где qm,j,j0 - пост, которые могут быть определены из нач условий.
Действительно, взяв вторую производную от q, по t и подставив её мы получим тождество
В уравнении qm называется амплитудой, аргумент 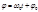 начальной фазой колебания (при t = 0). С одинаковым правоммы могли бы написать уравнение вида
начальной фазой колебания (при t = 0). С одинаковым правоммы могли бы написать уравнение вида 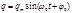
 Движения, описываемые уравнениями, являются тождественными. j0 для каждого частного случая в этих уравнениях имеет различное значение. Из этих уравнений видно, что заряд на обкладках конденсатора изменяется по гармоническому закону, поэтому эти уравнения называются уравнениями гармонического колебательного движения. График гармонического колебания показан на рисунке. Величина наибольшего заряда qm на обкладках конденсатора называется амплитудным значением заряда. Амплитуда – величина положительная, фаза определяет состояние колеблющейся системы в каждый момент времени. Величина начальной фазы зависит от начала отсчетавремени. Поскольку косинус - периодическая функция с периодом 2п, различные состояния системы, совершающей гармонические колебания, повторяются через период Т, за который фаза колебаний получает приращение, равное2п,т.е.
Движения, описываемые уравнениями, являются тождественными. j0 для каждого частного случая в этих уравнениях имеет различное значение. Из этих уравнений видно, что заряд на обкладках конденсатора изменяется по гармоническому закону, поэтому эти уравнения называются уравнениями гармонического колебательного движения. График гармонического колебания показан на рисунке. Величина наибольшего заряда qm на обкладках конденсатора называется амплитудным значением заряда. Амплитуда – величина положительная, фаза определяет состояние колеблющейся системы в каждый момент времени. Величина начальной фазы зависит от начала отсчетавремени. Поскольку косинус - периодическая функция с периодом 2п, различные состояния системы, совершающей гармонические колебания, повторяются через период Т, за который фаза колебаний получает приращение, равное2п,т.е. 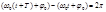 , откуда
, откуда 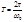 Число колебаний в единицу времени называется частотой колебаний. Очевидно, что
Число колебаний в единицу времени называется частотой колебаний. Очевидно, что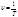 За единицу частоты принимается частота такого колебания, период которого равен I с. Эту единицу называют герцем (Гц,). Используются также кратные единицы: I кГц = I03 Гц(, I МГц» = I06 Гц.
За единицу частоты принимается частота такого колебания, период которого равен I с. Эту единицу называют герцем (Гц,). Используются также кратные единицы: I кГц = I03 Гц(, I МГц» = I06 Гц.
Из этого следует, что 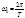
w, представляет собственную частоту колебаний контура. Она называется циклической частотой и равна числу колебаний за 2п секунд. Из этих уравнений получается соотношение 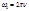 следует, что
следует, что 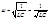
Подставив, получим 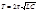 Разделим левую и правую части выражения на С , получим
Разделим левую и правую части выражения на С , получим
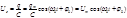
Продифференцировав функцию по времени, получим выражение для силы тока 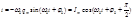
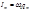
Сопоставив формулы,заключаем, что в момент, когда ток достигает максимального значения, заряд (а также напряжение) обращается в нуль, и наоборот. Это происходит вследствие того, что между током и напряжением сдвиг по фазе равен п/2.
5. Энергетические превращения происходящие при гарм - их колебаниях.
В некоторый момент времени t энергия электрического поля конденсатора равна:
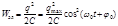
А энергия магнитного поля:
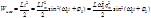
Полная энергия колебания равна сумме:
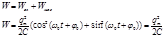 Таким образом в процессе колебаний изменяется только энергия электрического и магнитного полей, полная энергия колебаний контура остается неизменной и равной наибольшей энергии конденсатора qm2/2C или наибольшей энергии магнитного поля LIm2/2. Энергия переходит из одного вида в другой. Обратим внимание на то что энергия колебаний пропорциональна квадрату амплитуды значений заряда или силы тока.
Таким образом в процессе колебаний изменяется только энергия электрического и магнитного полей, полная энергия колебаний контура остается неизменной и равной наибольшей энергии конденсатора qm2/2C или наибольшей энергии магнитного поля LIm2/2. Энергия переходит из одного вида в другой. Обратим внимание на то что энергия колебаний пропорциональна квадрату амплитуды значений заряда или силы тока.
6. Сложение 2 гарм колеб одного напр и одинак частоты
При разл расчетах прих-ся опред переменный ток как сумму двух или нескольких переменных токов или какое-нибудь напряжение как сумму нескольких напряжений. При этом суммируемые токи или напряжения могут иметь разл амплитуды и быть сдвинутыми по фазе. Сложение их можно выполн аналитически или графически, но первый способ более громоздкий.
Рассмотрим вначале, какое результ колеб получ при слож двух колеб, одинаково направленных и одинаковой частоты, имеющих разные начальные фазы и амплитуды. Пусть
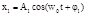
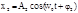 (1)
(1)
Результирзнач X определится как сумма:
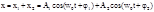 (2)
(2)
рис 1
Выпол это сложение графич. Предст оба колеб-я векторами амплит. 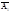 и
и 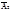 и будем вращ их против час. стрелки с один. угловой скоростью w0 (рис. 1). Тогда угол между векторами будет все время оставаться равным j2-j1.Т.к. x=x1+x2,то результ колеб. может быть изображено вектором амплитуды
и будем вращ их против час. стрелки с один. угловой скоростью w0 (рис. 1). Тогда угол между векторами будет все время оставаться равным j2-j1.Т.к. x=x1+x2,то результ колеб. может быть изображено вектором амплитуды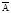 получ геометрич сложением векторов
получ геометрич сложением векторов 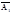 и
и 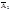 .
.
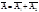
Из рис 1 имеем 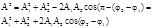 (3)
(3)
Таким образом, вектор 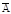 со временем не меняется и вращается с угловой скоростью w0 . Отсюда след, что результ колебание
со временем не меняется и вращается с угловой скоростью w0 . Отсюда след, что результ колебание 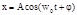 предст собой гармонич колеб. Нач фаза этого колеб опред извыражения:
предст собой гармонич колеб. Нач фаза этого колеб опред извыражения:
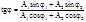
Из формулы (3) видно, что амплитуда результ колеб зависит от разн фаз (j2-j1) слагаемых колебаний. Рассмотрим частные случаи.
1. Разность фаз кратна четному числуp , т.е. j2-j1 = ±2mp,
где m, = 0,1,2......
Тогда колеб происх в одинаковых фазах и ампл-х результ колеб (рис.2) равна А=А1+А2
2. Разность фаз кратна нечетному числа p , т.е. j2-j1=±(2m+1)p
рис 2
где m - 0,1,2,.... В этомслучае колебания происходят в противофазе и амплитуда резервирующ колеб (рис.3) равна А=|А2+А1| В частности, если А1=А2, то А=0
рис 3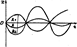
т.е. колебания гасят друг друга.
Если разн фаз складыв колеб имеет произв знач, то амплитуда результир колеб заключ в пределах 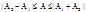
Колебания, имеяцие одинаковые частоты и не меняющийся со временем разность фаз, называют когерентными колебаниями. Полученные результаты сложения когерентных гармонических колебаний будут использованы при рассмотрении явления интерференции электромагнитных волн.
7. Слож 2 гарм колеб одн направл с мало отлич частотами
Если частоты складываемых колеб неодинаковы то векторы 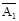 и
и 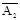 на векторной диаграмме будут вращаться с различной скорость. Тогда результ.вектор
на векторной диаграмме будут вращаться с различной скорость. Тогда результ.вектор 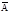 будет меняться по величине и вращ. с непостоянной скоростью. След, результ. колеб. будет негармонич.
будет меняться по величине и вращ. с непостоянной скоростью. След, результ. колеб. будет негармонич.
Особый интерес представляет случай, когда два складываемых колебания имеют одинаковые амплитуды и мало отличаются по частоте. Положим нач фазы колебаний равными нулю. Тогда уравнения колебаний примут следующий вид: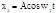
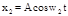 (1), где w2-w1=Dw<<w1 w2=w1+Dw
(1), где w2-w1=Dw<<w1 w2=w1+Dw
Складывая выражения (1), получим x=x1+x2=A(cosw1t+cosw2t)=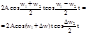
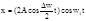 (2)
(2)
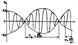
рис 1 Заключ в скобки множитель в формуле (2) изменяется значительно медл, чем 2 множитель. Ввиду условия Dw<<w за то время, за кот множитель cosw1t совершит неск колеб, множитель, стоящий в скобках, почти не изменится. Это дает основание рассм колебание (2) как гармоническое колебание частоты w1 , ампл котор. медленно изменяется с частотой по закону | 2Acos(Dw/2)*t | Знак модуля стоит потому, что по опред амплитуда-величина положительная. Отсюда частота колеб амплитв 2 раза превыш частоту, стоящую под знаком модуля, т.е. равна Dw. Уравнение (2) можно переписать в виде: 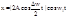 (3)
(3)
График функции (3) представлен на рисунке 1
Такие колебания называются биениями, а частота пульсаций амплитуда назыв частотой биения. Она равна Dw.