Тема 11. Статистическая связь между явлениями
Тема 11. Статистическая связь между явлениями
Построение моделей взаимосвязей включает ряд этапов. 1. Предварительный априорный анализ изучаемого явления. 2. Сбор исходных данных и их первичная статистическая обработка.Пример 1.
Таблица 1
Стоимость основных фондов и выпуск продукции по группе заводов
Для определения формы связи построим корреляционное поле. Отложим на оси абсцисс значения факторного признака (х), а на оси ординат – значение… Допустим, что между стоимостью основных фондов и выпуском продукции существует…Таблица 2
| Группы семей со среднедушевым совокупным доходом в месяц, ден. ед. | Расходы на питание, ден. ед. | |
| фактические (эмпирические) | расчетные | |
| 50,1 – 75,0 75,1 – 100,0 100,1 – 125,0 125,1 – 150,0 150,1 – 175,0 175,1 – 200,0 | 1528,31 1657,10 1760,36 1847,46 1923,20 1990,58 |
Расходы на питание выберем в качестве результативного признака (у), уровень среднедушевого совокупного дохода – в качестве независимой переменной х (К = 1), влияющей на уровень у. Число наблюдений n = 6. Для сгруппированных бюджетных данных определено следующее уравнение, отражающее имеющуюся взаимосвязь:
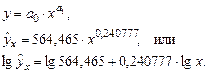
Рассчитанный F-критерий (Fнабл) составил 455,896.
Воспользуемся таблицами для определения F-критического.
Пусть a = 0,01; V1 = K = 1; V2 = n – (K + 1) = 6 – 1 – 1 = 4.
Тогда Fкрит~21,20.
Fнабл (455,896) > Fкрит (21,20), следовательно, гипотеза о равенстве 0 коэффициентов при х отвергается и с вероятностью 99% можно заключить, что уравнение регрессии значимо, то есть хорошо представляет все имеющиеся причинно-следственные связи.
При изучении корреляционной связи можно выяснить не только форму, но и тесноту связи между факторным и результативным признаками.
Чтобы измерить тесноту прямолинейной связи, рассчитывают коэффициент корреляции:
 .
.
Коэффициент корреляции принимает значения от –1 до +1, чем ближе к 1, тем выше зависимость.
При 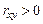 – связь прямая,
– связь прямая,  – связь обратная,
– связь обратная, 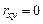 – связь отсутствует.
– связь отсутствует.
В зависимости от того, насколько  приближается к ±1, различают связь слабую, умеренную, заметную, высокую, тесную и весьма тесную.
приближается к ±1, различают связь слабую, умеренную, заметную, высокую, тесную и весьма тесную.
Вычислим коэффициент корреляции по данным табл. 1.
Таблица 3
| Номер завода | х | у | 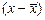
| 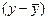
| 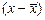 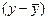
| 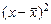
| 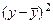
| х×у |
| 2,4 4,0 3,6 4,0 4,5 4,6 5,6 6,5 7,0 5,0 | –4,8 –2,8 –1,8 –0,8 –0,8 +0,2 +1,2 +2,2 +3,2 +4,2 | –2,32 –0,72 –1,12 –0,72 –0,22 –0,12 +0,88 +1,78 +2,28 +0,28 | +11,136 +2,016 +2,016 +0,576 +0,176 –0,024 +1,056 +3,916 +7,296 +1,176 | 23,04 7,84 3,24 0,64 0,64 0,04 1,44 4,84 10,24 17,64 | 5,38 0,52 1,25 0,52 0,05 0,01 0,77 3,17 5,20 0,08 | 14,4 32,0 32,4 40,0 45,0 50,6 67,2 84,5 98,0 75,0 | ||
| S | 47,2 | +29,340 | 69,60 | 16,96 | 539,1 |
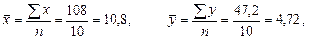
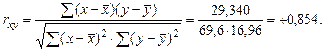
Таким образом, связь между стоимостью основных фондов и выпуском продукции прямая и высокая.
Коэффициент корреляции может быть исчислен и по формуле:
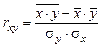 ,
,
где  ;
;  – среднее квадратическое отклонение результативного признака;
– среднее квадратическое отклонение результативного признака;  – среднее квадратическое отклонение факторного признака.
– среднее квадратическое отклонение факторного признака.
По данным табл. 2 исчислим
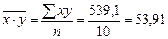 ,
,
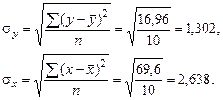
Подставим необходимые данные в формулу:
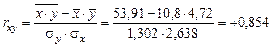 .
.
В случае нелинейной зависимости между признаками для измерения тесноты связи применяют корреляционное отношение, которое исчисляется по формуле:
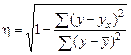 ,
,
где у – фактические значения;  – среднее значение; ух – теоретические (выравненные) значения переменной величины.
– среднее значение; ух – теоретические (выравненные) значения переменной величины.
Корреляционное отношение по своему абсолютному значению колеблется в пределах от 0 до 1.
Пример 3. Имеются данные о душевом доходе и потреблении мяса семей различного состава (табл. 4).
Таблица 4
| Средний доход на члена семьи за месяц, руб. х1 | Число членов семьи, х2 | Душевое потребление мяса за месяц, кг у | 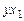
| 
| 
| 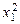
| 
| 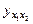
|
| 3,0 3,3 4,2 5,0 4,5 6,8 6,2 7,0 | 210,0 280,5 378,0 500,0 562,5 1020,0 806,0 1120,0 | 12,0 13,2 12,6 15,0 9,0 13,6 6,2 7,0 | 3,0 3,5 4,0 4,6 5,5 6,4 5,9 7,0 | |||||
| Итого: 910 | 40,0 | 4877,0 | 88,6 | 40,0 | ||||
| Среднее значение: 113,75 | 2,5 | 5,0 | 609,63 | 11,075 | 253,75 |
Допустим, что связь в данном случае между у, х1 и х2 прямолинейная. Подставим данные табл. 4. в систему нормальных уравнений:

Для решения системы нормальных уравнений разделим все члены уравнений на коэффициент при 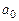 :
:

Вычтем теперь из первого уравнения второе и третье и получим:
–0,36 = –8,06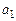 + 0,27a2
+ 0,27a2
0,57 = 12,25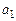 – 0,5a2.
– 0,5a2.
Разделим все члены уравнений на коэффициенты при a2 и вычтем из первого уравнения второе:

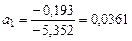 .
.
Подставив значение параметра 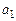 в уравнение, получим:
в уравнение, получим:
–1,140 = –24,5×0,0361 +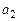 ,
,
откуда
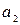 = –1,140 + 0,8844 = 0,2556.
= –1,140 + 0,8844 = 0,2556.
Аналогично определяем значение параметра  , которое будет равно
, которое будет равно  .
.
Уравнение множественной регрессии, характеризующее зависимость потребления мяса от душевого дохода и числа членов семьи, будет иметь вид:
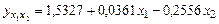 .
.
Параметр 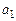 показывает, что с ростом дохода на одного члена семьи на 1 руб. расходы на потребление мяса увеличиваются в среднем на душу на 0,0361 руб., а параметр
показывает, что с ростом дохода на одного члена семьи на 1 руб. расходы на потребление мяса увеличиваются в среднем на душу на 0,0361 руб., а параметр 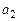 показывает, что с увеличением размера семьи на одного человека потребление мяса уменьшается в среднем на 0,2556 кг.
показывает, что с увеличением размера семьи на одного человека потребление мяса уменьшается в среднем на 0,2556 кг.
Подставим в уравнение множественной регрессии эмпирические значения  , получим теоретические значения
, получим теоретические значения 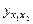 (см. табл. 4).
(см. табл. 4).
При определении тесноты связи для множественной зависимости пользуются коэффициентом множественной (совокупной) корреляции, предварительно исчислив коэффициенты парной корреляции. Для нашего примера коэффициент множественной корреляции имеет вид:
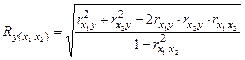 ,
,
где  – парные коэффициенты корреляции.
– парные коэффициенты корреляции.
Коэффициент множественной корреляции колеблется в пределах от 0 до 1. Чем он ближе к 1, тем в большей мере учтены факторы, определяющие конечный результат.
По данным табл. 4 рассчитаем коэффициент множественной корреляции.
Таблица 5
( ) )
| 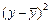
| 
| 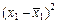
| 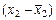
| 
|
| –2,0 –1,7 –0,8 0,5 1,8 1,2 2,0 | 4,00 2,89 0,64 0,00 0,25 3,24 1,44 4,00 | –43,75 –28,75 –23,75 –13,75 11,25 36,25 16,25 46,25 | 1914,06 826,56 564,06 189,06 126,56 1314,06 264,06 2139,06 | +1,5 +1,5 +0,5 +0,5 –0,5 –0,5 –1,5 –1,5 | 2,25 2,25 0,25 0,25 0,25 0,25 2,25 2,25 |
| 16,46 | 7337,5 |
Для определения парных коэффициентов корреляции вычисляем:
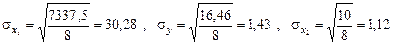 .
.
Парные коэффициенты корреляции определяются по следующим формулам:
 ,
,
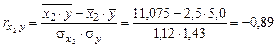 ,
,
 .
.
Исчислим коэффициент множественной корреляции:

Сравнивая парные коэффициенты корреляции с коэффициентом множественной корреляции, видим, что связь между результативным признаком (y) и двумя факторами (x1 и x2) является более полной, чем с каждым фактором в отдельности.
Поскольку факторные признаки действуют не изолированно, а во взаимосвязи, то может возникнуть задача определения тесноты связи между результативным признаком и одним из факторных при постоянных значениях прочих факторов. Она решается при помощи частных коэффициентов корреляции. Например, при линейной связи частный коэффициент корреляции между x1 и y при постоянном x2 исчисляется по следующей формуле:
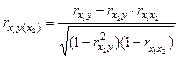 .
.
Частный коэффициент корреляции при изучении зависимости у от 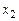 при постоянном
при постоянном  определяется по формуле:
определяется по формуле:
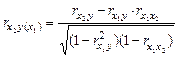 .
.
В нашем примере частный коэффициент корреляции между у и x1 при неизменном значении x2 равен:
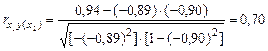 .
.
Частный коэффициент корреляции между у и x2 при неизменном значении фактора x1 равен:
 .
.
Если сравнить исчисленные коэффициенты частной корреляции с соответствующими коэффициентами парной корреляции, то окажется, что последние значительно больше первых, то есть они преувеличивают меру связи между результативным и факторным признаком. Это объясняется тем, что факторы взаимно коррелируют между собой. Коэффициент же частной корреляции определяет действие каждого фактора при неизмененном значении остальных факторов. Поэтому они более точно определяют тесноту связи.
В отдельных случаях при ориентировочной оценке тесноты связи пользуются приближенными показателями, не требующими сложных, трудоемких расчетов. К ним относятся: коэффициент корреляции знаков Фехнера, коэффициент корреляции рангов, коэффициент ассоциации и коэффициент сопряженности.
Коэффициент корреляции знаков Фехнера основан на сопоставлении знаков отклонений от средней и подсчете числа случаев совпадения знаков:
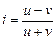 и лежит в пределах –1 £ i £ +1.
и лежит в пределах –1 £ i £ +1.
где u – число пар с одинаковыми знаками отклонений х и у от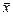 и
и ; v – число пар с разными знаками отклонений х и у от
; v – число пар с разными знаками отклонений х и у от 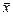 и
и . Чем ближе коэффициент к 1, тем теснее связь.
. Чем ближе коэффициент к 1, тем теснее связь.
Исчислим i по данным табл. 1.
 .
.
Это значит, что связь между стоимостью основных фондов и выпуском продукции прямая и высокая.
Коэффициент корреляции рангов Спирмена исчисляется не по первичным данным, а по рангам (порядковым номерам), которые присваиваются всем значениям изучаемых признаков, расположенным в порядке их возрастания. Если значения признака совпадают, то определяется средний ранг путем деления суммы рангов на число значений. Коэффициент корреляции рангов определяется по формуле:
 и лежит в пределах –1 £ r £ +1.
и лежит в пределах –1 £ r £ +1.
где d2 – квадрат разности рангов для каждой единицы; n – число наблюдений (число пар рангов).
Исчислим r по данным табл. 1.
Таблица 6
| Номер завода | Стоимость основных фондов, млн руб. х | Выпуск продукции, млн руб. у | Ранги | Разность рангов d | d2 | |
| по х | по у | |||||
| 2,4 4,0 3,6 4,0 4,5 4,6 5,6 6,5 7,0 5,0 | 4,5 4,5 | 3,5 3,5 | –1,5 +1 +1 –0,5 –1 –1 –1 +3 | 2,25 0,25 | ||
| 16,5 |
 .
.
Полученный ранговый коэффициент корреляции свидетельствует о наличии прямой тесной связи между величиной основных фондов и выпуском продукции.
Коэффициенты ассоциации и контингенции применяются для установления меры связи между двумя качественными альтернативными признаками. Для их вычисления строится комбинационная четырехклеточная таблица. Например, зависимость наличия отдельной квартиры от семейного положения (табл. 7).
Таблица 7
| Семейное положение | Имеют отдельную квартиру | Не имеют отдельной квартиры | Всего |
| Семейные Одинокие | a c | b d | a + b c + d |
| Всего: | а + c | b + d | a + b + c + d |
Коэффициент контингенции рассчитывается по формуле:
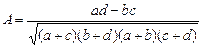 и лежит в пределах –1 £ A £ +1
и лежит в пределах –1 £ A £ +1
В качестве метода для установления ассоциативной связи может быть использован также коэффициент ассоциации Юла:
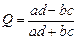 .
.
[1][1] Кейн Э. Экономическая статистика и эконометрия. Вып. 2. М., 1977. С. 25.